江西省吉安市遂川县高级中学2021-2022学年高二上学期第二次月考数学(文)试卷(B卷)(Word版含答案)
文档属性
| 名称 | 江西省吉安市遂川县高级中学2021-2022学年高二上学期第二次月考数学(文)试卷(B卷)(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-20 15:59:28 | ||
图片预览


文档简介
遂川县高级中学2021-2022学年高二上学期第二次月考
文科数学试题(B卷)
一、单选题
1.直线经过原点和,则它的倾斜角是( )
A.135° B.60° C.120° D.45°
2.边长为2的正三角形,其水平放置的直观图的面积为( )
A. B. C. D.
3.以下四个命题中,正确命题的个数是( )
①不共面的四点中,任意三点不共线;
②若点A,B,C,D共面,点A,B,C,E共面,则A,B,C,D,E共面;
③若直线a,b共面,直线a,c共面,则直线b,c共面;
④依次首尾相接的四条线段必共面.
A.0 B.1 C.2 D.3
4.设,则( )
A. B.
C. D.
5.下列说法正确的是( )
A.如果一个平面内有一条直线和另一个平面平行,那么这两个平面平行
B.如果一个平面内有无数条直线和另一个平面平行,那么这两个平面平行
C.如果一个平面内的任何直线都与另一个平面平行,那么这两个平面平行
D.如果两个平面平行于同一条直线,则这两个平面平行
6.若将面积为2的等腰直角三角形,以其一条直角边所在的直线为旋转轴旋转而成一个圆锥,则该圆锥的体积为( )
A. B. C. D.
7.已知,是两个不同平面,,是两不同直线,下列命题中不正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
8.已知数列为等差数列,其前项和为,,则( )
A.110 B.55 C.50 D.45
9.在中,是的中点,是的中点,若,则( )
A.1 B. C. D.
10.函数的图象向左平移个单位长度后得到函数的图象,且的图象关于轴对称,则的最小值为( )
A. B. C. D.
11.已知函数是R上的偶函数.若对于都有,且当时,,则的值为( )
A.1 B.﹣1 C.﹣2 D.2
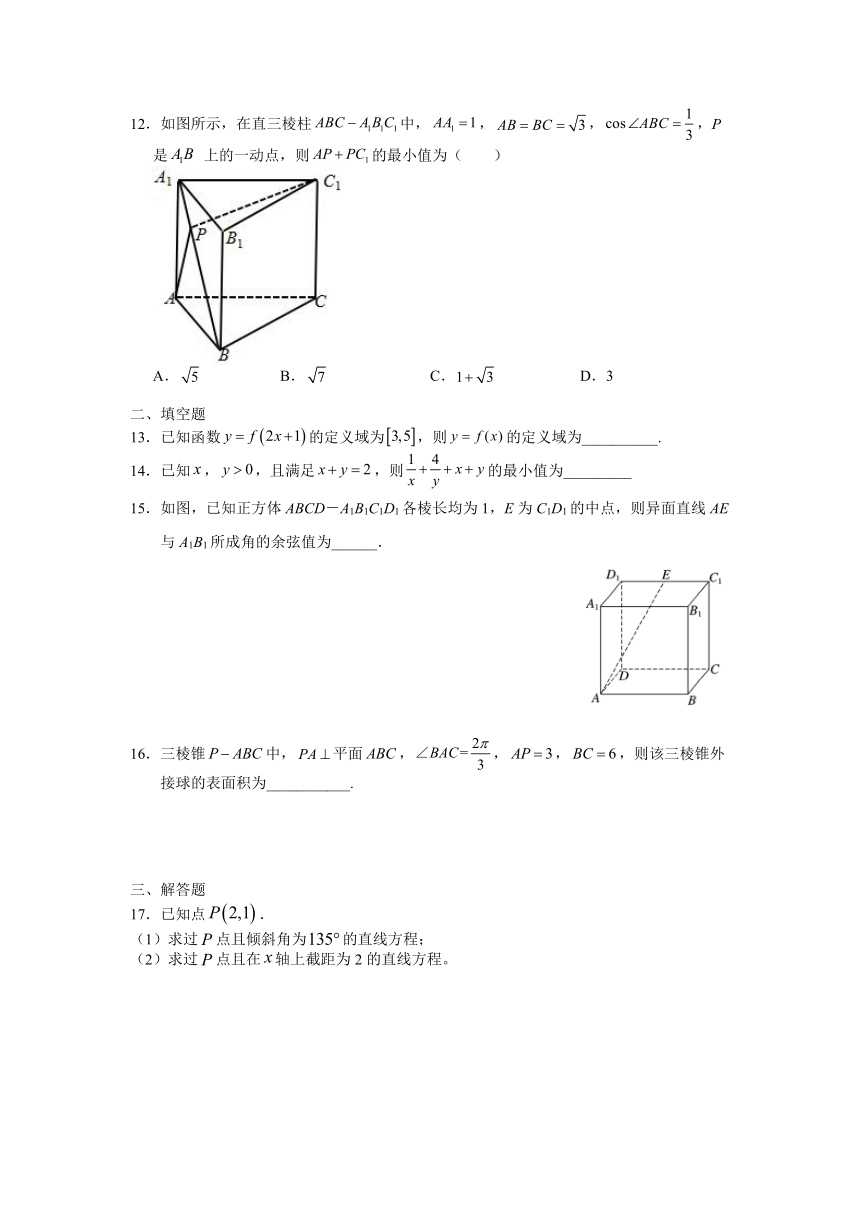
12.如图所示,在直三棱柱中,,,,P是 上的一动点,则的最小值为( )
A. B. C. D.3
二、填空题
13.已知函数的定义域为,则的定义域为__________.
14.已知,,且满足,则的最小值为_________
15.如图,已知正方体ABCD-A1B1C1D1各棱长均为1,E为C1D1的中点,则异面直线AE与A1B1所成角的余弦值为______.
16.三棱锥中,平面,,,,则该三棱锥外接球的表面积为___________.
三、解答题
17.已知点.
(1)求过点且倾斜角为的直线方程;
(2)求过点且在轴上截距为2的直线方程。
18.在中,a b c分别是角A B C的对边,且.
(1)求角B的大小;
(2)若,求的面积和周长.
19.已知点,分别是正方形的边,的中点.现将四边形沿折起,使二面角为直二面角,如图所示.
(1)若点,分别是,的中点,求证:平面;
(2)求直线与平面所成角的正弦值.
20.如图,已知多面体ABCDEF中的四边形ABCD是正方形,是以BC为斜边的等腰直角三角形,,是等边三角形,M是棱BC的中点,且.
(1)证明:平面BCF.
(2)设,求多面体ABCDEF的体积.
21.如图,在三棱锥P-ABC中,PA⊥平面ABC,,PA=2, AB= AC=4,点D、E、F分别为BC、AB、AC的中点.
(1)求证:EF⊥平面PAD;
(2)求点A到平面PEF的距离.
22.已知数列的前项和为,,,
(1)求证:数列为等差数列;
(2)令bn=2nan,求数列{bn}的前n项和Tn.
参考答案
1.A
解:设倾斜角为,则,因为,所以,故选:A
2.D
根据原图作出直观图如图所示:
在中,,,,
所以中,边上的高为,
所以的面积为,所以水平放置的直观图的面积为,
3.B
①假设任意三点共线,由于一条直线与直线外的一点确定一个平面,故四点共面,因此与不共面的四点矛盾,故假设不成立,即不共面的四点中,任意三点不共线,显然是正确的;②若A,B,C三点共线,则A,B,C,D,E五点不一定共面,故不正确;③构造长方体或正方体,如图,显然b,c异面,故不正确;④空间四边形中四条线段不共面,故不正确.故正确的个数为1.
故选:B.
4.A
5.C
A:如果一个平面内有一条直线和另一个平面平行,则这两个平面平行、重合、相交,错误;
B:如果一个平面内有无数条直线和另一个平面平行,则这两个平面平行、重合、相交,错误;C:如果一个平面内的任何直线都与另一个平面平行,则这两个平面平行,正确;
D:如果两个平面平行于同一条直线,则这两个平面平行、重合、相交,错误;
故选:C
6.D
由等腰直角三角形的面积为2,得其直角边长为2,
所以经过旋转得到圆锥的高为2,底面圆半径为2,
所以圆锥的体积为:.
故选:D
7.C对于A,若,则取内任意两条相交直线,使得,,又,则,,由线面垂直的判定定理得,故A正确;
对于B,垂直于同一条直线的两个平面平行,故B正确;
对于C,若,,如图,
设,平面为平面,,设平面为平面,,则,故C错误;对于D,由面面垂直的判定定理可得,故D正确;故选:C.
8.B在等差数列中,,于是得,所以.故选:B
9.D
解:∵是的中点,,为的中点,
∴
,
∵,∴,,
∴,故选:D.
10.C由题可得,的图象关于轴对称,
,解得,,, 则的最小值为.故选:C.
11.A【详解】因为为上的偶函数,所以,又因为对于,都有,所以函数的周期,且当时,,
所以故选:A
12.B连接,得,以所在直线为轴,将所在平面旋转到平面,
设点的新位置为,连接,则有.
当三点共线时,则即为的最小值.
在三角形ABC中,,,由余弦定理得:,所以,即
在三角形中,,,由勾股定理可得:,且.同理可求:因为,所以为等边三角形,所以,所以在三角形中,,,
由余弦定理得:.
故选B.
13.14.因为,所以
,当且仅当即时等号成立,所以的最小值为.故答案为:.
15.解:连接,
在正方体ABCD-A1B1C1D1中,,所以即为异面直线AE与A1B1所成角的平面角,又平面,平面,所以,
在中, E为C1D1的中点,所以,
在中,AE=,所以.
16.
如图,设是的外心,过作平面,且,则是三棱锥外接球的球心,
由正弦定理得,,
平面,平面,所以,而平面,则,
是直角梯形,,,
所以球表面积为.
故答案为:.
17.(1);(2)
18.(1);(2),.
(1)由余弦定理,得,
将上式代入,整理得,
∴,∵角B为的内角,∴.
(2)在中,,
在中,由余弦定理,将,
代入得,∴,
∴,的周长为.
19.(1)证明见解析;(2).
证明:(1)连接,
设点为的中点,连接,,
在中,又因为点为中点,
所以.
同理可证得,
又因为,分别为正方形的边,的中点,
故,所以.
又因为,所以平面平面.
又因为平面,所以平面.
(2)因为为正方形,,分别是,的中点,
所以四边形为矩形,则.
又因为二面角为直二面角,平面平面,平面,
所以平面,
则为直线在平面内的射影,
因为为直线与平面所成的角.
不妨设正方形边长为,则,在中,,因为平面,平面,所以,在中,,
,即为直线与平面所成角的正弦值.
20.(1)证明见解析;(2).
(1)因为四边形ABCD是正方形,所以.
又,所以平面BCF.
(2)如图,因为,过AD作平行于平面BCF的平面,
将多面体ABCDEF补形成三棱柱,由(1)知三楼柱是直棱柱.
因为是以BC为斜边的等腰直角三角形,且,
所以,所以.设AD的中点为G,连接EG,NG,可知,所以,
所以.故.
21.(Ⅰ)PA⊥平面,又点、分别为、的中点
在中,AB=AC
平面.
(Ⅱ)设与相交于点,连接.
∵EF⊥平面平面平面,
过做于,则平面,故线段为点到平面的距离
在中,,
即点到平面的距离为.
22.(1)证明见解析;(2)Tn=(2n+1)2n+1-2.
(1)证明:由nSn+1-(n+1)Sn=n2+n得,又=5,
所以数列是首项为5,公差为1的等差数列.
(2)由(1)可知=5+(n-1)=n+4,所以Sn=n2+4n.
当n≥2时,an=Sn-Sn-1=n2+4n-(n-1)2-4(n-1)=2n+3.
又a1=5也符合上式,所以an=2n+3(n∈N*),
所以bn=(2n+3)2n,
所以Tn=5×2+7×22+9×23+…+(2n+3)2n,①
2Tn=5×22+7×23+9×24+…+(2n+1)2n+(2n+3)·2n+1,②
所以②-①得Tn=(2n+3)2n+1-10-(23+24+…+2n+1)
=(2n+3)2n+1-10-
=(2n+3)2n+1-10-(2n+2-8)
=(2n+1)2n+1-2.
文科数学试题(B卷)
一、单选题
1.直线经过原点和,则它的倾斜角是( )
A.135° B.60° C.120° D.45°
2.边长为2的正三角形,其水平放置的直观图的面积为( )
A. B. C. D.
3.以下四个命题中,正确命题的个数是( )
①不共面的四点中,任意三点不共线;
②若点A,B,C,D共面,点A,B,C,E共面,则A,B,C,D,E共面;
③若直线a,b共面,直线a,c共面,则直线b,c共面;
④依次首尾相接的四条线段必共面.
A.0 B.1 C.2 D.3
4.设,则( )
A. B.
C. D.
5.下列说法正确的是( )
A.如果一个平面内有一条直线和另一个平面平行,那么这两个平面平行
B.如果一个平面内有无数条直线和另一个平面平行,那么这两个平面平行
C.如果一个平面内的任何直线都与另一个平面平行,那么这两个平面平行
D.如果两个平面平行于同一条直线,则这两个平面平行
6.若将面积为2的等腰直角三角形,以其一条直角边所在的直线为旋转轴旋转而成一个圆锥,则该圆锥的体积为( )
A. B. C. D.
7.已知,是两个不同平面,,是两不同直线,下列命题中不正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
8.已知数列为等差数列,其前项和为,,则( )
A.110 B.55 C.50 D.45
9.在中,是的中点,是的中点,若,则( )
A.1 B. C. D.
10.函数的图象向左平移个单位长度后得到函数的图象,且的图象关于轴对称,则的最小值为( )
A. B. C. D.
11.已知函数是R上的偶函数.若对于都有,且当时,,则的值为( )
A.1 B.﹣1 C.﹣2 D.2
12.如图所示,在直三棱柱中,,,,P是 上的一动点,则的最小值为( )
A. B. C. D.3
二、填空题
13.已知函数的定义域为,则的定义域为__________.
14.已知,,且满足,则的最小值为_________
15.如图,已知正方体ABCD-A1B1C1D1各棱长均为1,E为C1D1的中点,则异面直线AE与A1B1所成角的余弦值为______.
16.三棱锥中,平面,,,,则该三棱锥外接球的表面积为___________.
三、解答题
17.已知点.
(1)求过点且倾斜角为的直线方程;
(2)求过点且在轴上截距为2的直线方程。
18.在中,a b c分别是角A B C的对边,且.
(1)求角B的大小;
(2)若,求的面积和周长.
19.已知点,分别是正方形的边,的中点.现将四边形沿折起,使二面角为直二面角,如图所示.
(1)若点,分别是,的中点,求证:平面;
(2)求直线与平面所成角的正弦值.
20.如图,已知多面体ABCDEF中的四边形ABCD是正方形,是以BC为斜边的等腰直角三角形,,是等边三角形,M是棱BC的中点,且.
(1)证明:平面BCF.
(2)设,求多面体ABCDEF的体积.
21.如图,在三棱锥P-ABC中,PA⊥平面ABC,,PA=2, AB= AC=4,点D、E、F分别为BC、AB、AC的中点.
(1)求证:EF⊥平面PAD;
(2)求点A到平面PEF的距离.
22.已知数列的前项和为,,,
(1)求证:数列为等差数列;
(2)令bn=2nan,求数列{bn}的前n项和Tn.
参考答案
1.A
解:设倾斜角为,则,因为,所以,故选:A
2.D
根据原图作出直观图如图所示:
在中,,,,
所以中,边上的高为,
所以的面积为,所以水平放置的直观图的面积为,
3.B
①假设任意三点共线,由于一条直线与直线外的一点确定一个平面,故四点共面,因此与不共面的四点矛盾,故假设不成立,即不共面的四点中,任意三点不共线,显然是正确的;②若A,B,C三点共线,则A,B,C,D,E五点不一定共面,故不正确;③构造长方体或正方体,如图,显然b,c异面,故不正确;④空间四边形中四条线段不共面,故不正确.故正确的个数为1.
故选:B.
4.A
5.C
A:如果一个平面内有一条直线和另一个平面平行,则这两个平面平行、重合、相交,错误;
B:如果一个平面内有无数条直线和另一个平面平行,则这两个平面平行、重合、相交,错误;C:如果一个平面内的任何直线都与另一个平面平行,则这两个平面平行,正确;
D:如果两个平面平行于同一条直线,则这两个平面平行、重合、相交,错误;
故选:C
6.D
由等腰直角三角形的面积为2,得其直角边长为2,
所以经过旋转得到圆锥的高为2,底面圆半径为2,
所以圆锥的体积为:.
故选:D
7.C对于A,若,则取内任意两条相交直线,使得,,又,则,,由线面垂直的判定定理得,故A正确;
对于B,垂直于同一条直线的两个平面平行,故B正确;
对于C,若,,如图,
设,平面为平面,,设平面为平面,,则,故C错误;对于D,由面面垂直的判定定理可得,故D正确;故选:C.
8.B在等差数列中,,于是得,所以.故选:B
9.D
解:∵是的中点,,为的中点,
∴
,
∵,∴,,
∴,故选:D.
10.C由题可得,的图象关于轴对称,
,解得,,, 则的最小值为.故选:C.
11.A【详解】因为为上的偶函数,所以,又因为对于,都有,所以函数的周期,且当时,,
所以故选:A
12.B连接,得,以所在直线为轴,将所在平面旋转到平面,
设点的新位置为,连接,则有.
当三点共线时,则即为的最小值.
在三角形ABC中,,,由余弦定理得:,所以,即
在三角形中,,,由勾股定理可得:,且.同理可求:因为,所以为等边三角形,所以,所以在三角形中,,,
由余弦定理得:.
故选B.
13.14.因为,所以
,当且仅当即时等号成立,所以的最小值为.故答案为:.
15.解:连接,
在正方体ABCD-A1B1C1D1中,,所以即为异面直线AE与A1B1所成角的平面角,又平面,平面,所以,
在中, E为C1D1的中点,所以,
在中,AE=,所以.
16.
如图,设是的外心,过作平面,且,则是三棱锥外接球的球心,
由正弦定理得,,
平面,平面,所以,而平面,则,
是直角梯形,,,
所以球表面积为.
故答案为:.
17.(1);(2)
18.(1);(2),.
(1)由余弦定理,得,
将上式代入,整理得,
∴,∵角B为的内角,∴.
(2)在中,,
在中,由余弦定理,将,
代入得,∴,
∴,的周长为.
19.(1)证明见解析;(2).
证明:(1)连接,
设点为的中点,连接,,
在中,又因为点为中点,
所以.
同理可证得,
又因为,分别为正方形的边,的中点,
故,所以.
又因为,所以平面平面.
又因为平面,所以平面.
(2)因为为正方形,,分别是,的中点,
所以四边形为矩形,则.
又因为二面角为直二面角,平面平面,平面,
所以平面,
则为直线在平面内的射影,
因为为直线与平面所成的角.
不妨设正方形边长为,则,在中,,因为平面,平面,所以,在中,,
,即为直线与平面所成角的正弦值.
20.(1)证明见解析;(2).
(1)因为四边形ABCD是正方形,所以.
又,所以平面BCF.
(2)如图,因为,过AD作平行于平面BCF的平面,
将多面体ABCDEF补形成三棱柱,由(1)知三楼柱是直棱柱.
因为是以BC为斜边的等腰直角三角形,且,
所以,所以.设AD的中点为G,连接EG,NG,可知,所以,
所以.故.
21.(Ⅰ)PA⊥平面,又点、分别为、的中点
在中,AB=AC
平面.
(Ⅱ)设与相交于点,连接.
∵EF⊥平面平面平面,
过做于,则平面,故线段为点到平面的距离
在中,,
即点到平面的距离为.
22.(1)证明见解析;(2)Tn=(2n+1)2n+1-2.
(1)证明:由nSn+1-(n+1)Sn=n2+n得,又=5,
所以数列是首项为5,公差为1的等差数列.
(2)由(1)可知=5+(n-1)=n+4,所以Sn=n2+4n.
当n≥2时,an=Sn-Sn-1=n2+4n-(n-1)2-4(n-1)=2n+3.
又a1=5也符合上式,所以an=2n+3(n∈N*),
所以bn=(2n+3)2n,
所以Tn=5×2+7×22+9×23+…+(2n+3)2n,①
2Tn=5×22+7×23+9×24+…+(2n+1)2n+(2n+3)·2n+1,②
所以②-①得Tn=(2n+3)2n+1-10-(23+24+…+2n+1)
=(2n+3)2n+1-10-
=(2n+3)2n+1-10-(2n+2-8)
=(2n+1)2n+1-2.
同课章节目录
