28.2.2应用举例 第2课时 课件(共26张PPT)
文档属性
| 名称 | 28.2.2应用举例 第2课时 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 00:00:00 | ||
图片预览


文档简介
(共26张PPT)
28.2.2应用举例
---第2课时
人教版 九年级下
教学目标
1. 正确理解方向角、坡度的概念. (重点)
2. 能运用解直角三角形知识解决方向角、坡度的问题;进一步提
高运用解直角三角形知识分析解决问题的综合能力.
(重点、难点)
情境导入
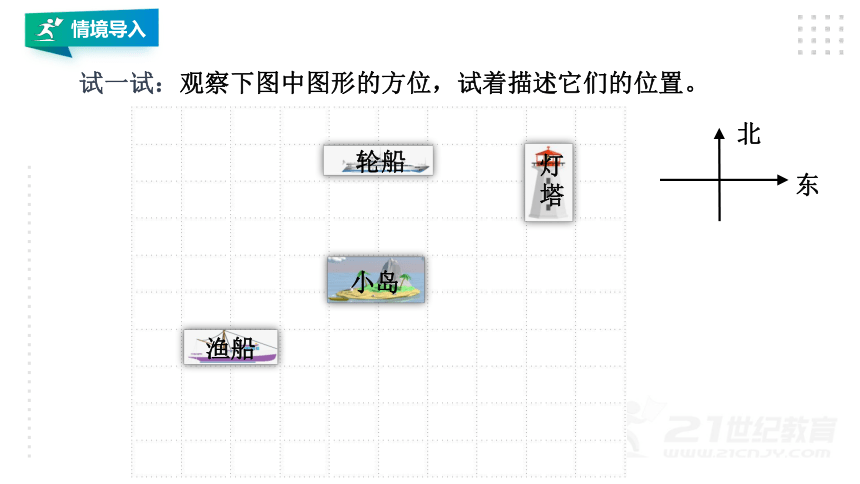
试一试:观察下图中图形的方位,试着描述它们的位置。
小岛
轮船
渔船
灯
塔
东
北
回顾旧知
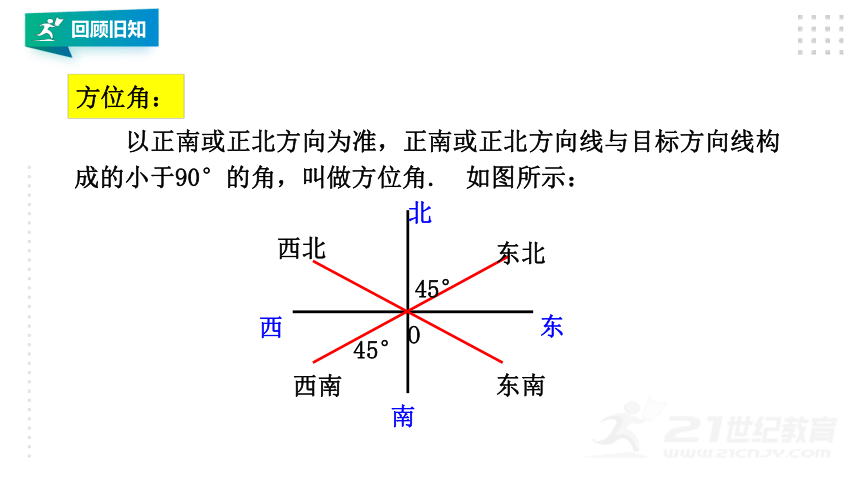
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于90°的角,叫做方位角. 如图所示:
方位角:
45°
45°
西南
O
东北
东
西
北
南
西北
东南
典例精析
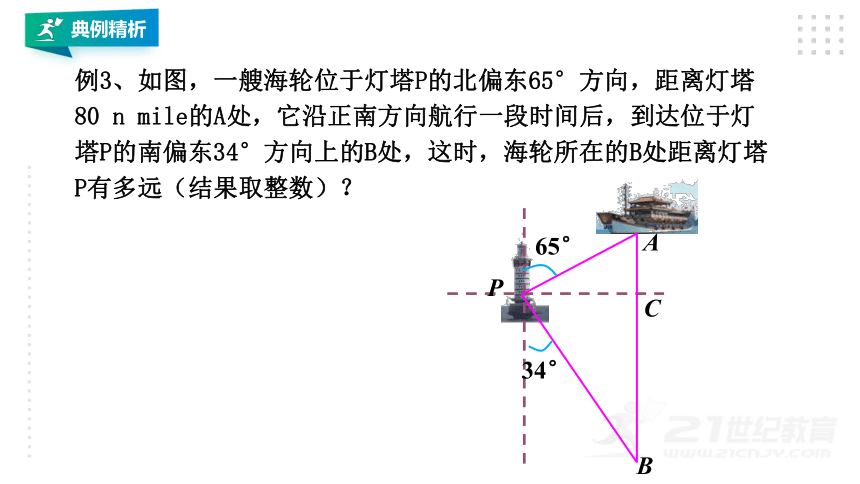
例3、如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔 80 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(结果取整数)?
65°
34°
P
B
C
A
典例精析
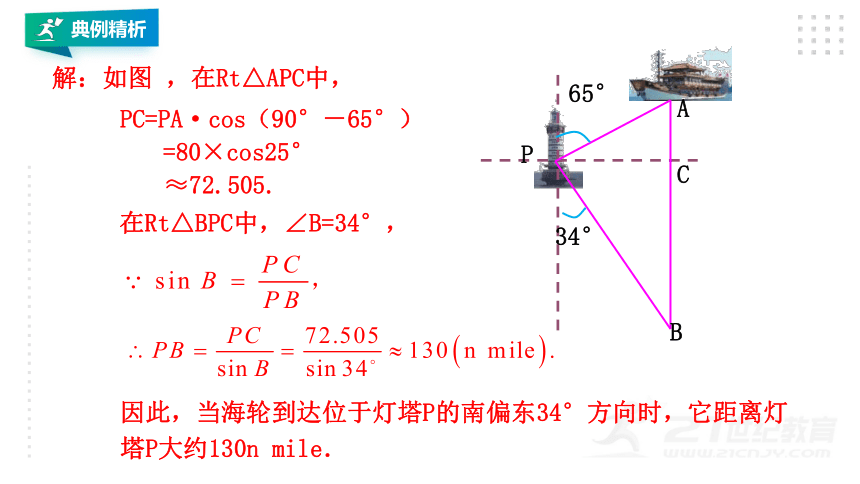
解:如图 ,在Rt△APC中,
PC=PA·cos(90°-65°)
=80×cos25°
≈72.505.
在Rt△BPC中,∠B=34°,
因此,当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130n mile.
65°
34°
P
B
C
A
趁热打铁
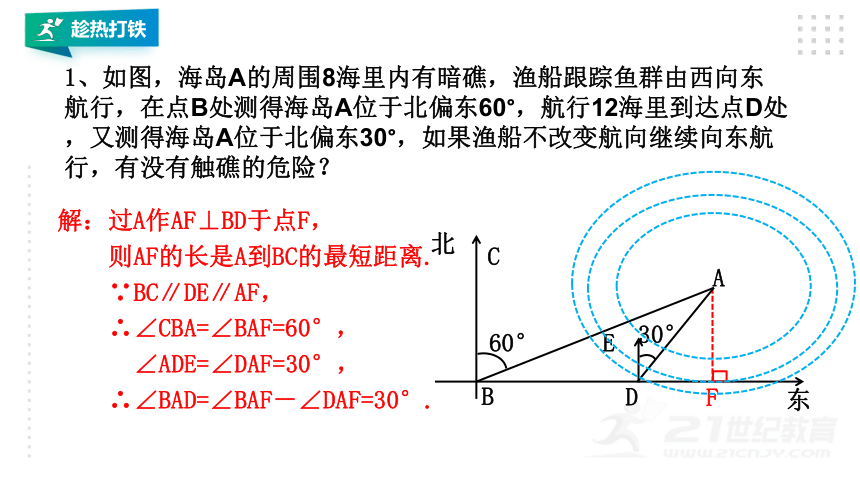
1、如图,海岛A的周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在点B处测得海岛A位于北偏东60°,航行12海里到达点D处,又测得海岛A位于北偏东30°,如果渔船不改变航向继续向东航行,有没有触礁的危险?
解:过A作AF⊥BD于点F,
则AF的长是A到BC的最短距离.
∵BC∥DE∥AF,
∴∠CBA=∠BAF=60°,
∠ADE=∠DAF=30°,
∴∠BAD=∠BAF-∠DAF=30°.
北
东
A
D
B
60°
30°
C
E
F
趁热打铁
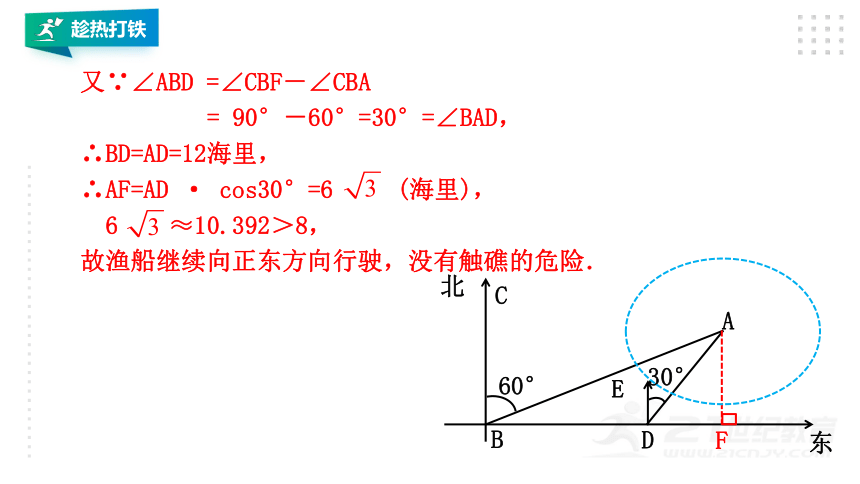
又∵∠ABD =∠CBF-∠CBA
= 90°-60°=30°=∠BAD,
∴BD=AD=12海里,
∴AF=AD · cos30°=6 (海里),
6 ≈10.392>8,
故渔船继续向正东方向行驶,没有触礁的危险.
北
东
A
D
B
60°
30°
C
E
F
合作探究
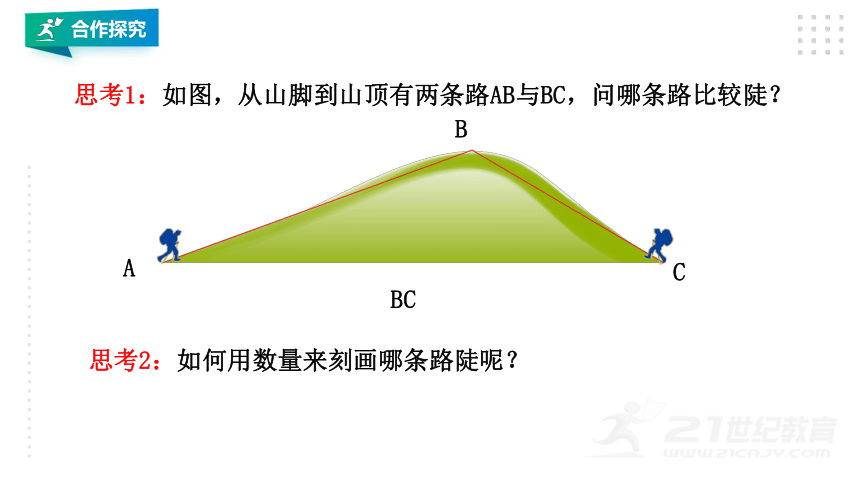
思考1:如图,从山脚到山顶有两条路AB与BC,问哪条路比较陡?
思考2:如何用数量来刻画哪条路陡呢?
A
B
C
BC
合作探究
α
l
h
1. 坡角
坡面与水平面的夹角叫做坡角,记作 α .
2. 坡度 (或坡比)
温馨提示:坡度通常写成 1∶m的形式,如i=1∶6.
如图所示,坡面的铅垂高度 (h) 和水
平长度 (l) 的比叫做坡面的坡度
(或坡比),记作i, 即 i = h : l .
坡面
水平面
3. 坡度与坡角的关系
即坡度等于坡角的正切值.
趁热打铁
1. 斜坡的坡度是 ,则坡角α =___度.
2. 斜坡的坡角是45° ,则坡比是 _____.
3. 斜坡长是12米,坡高6米,则坡比是_______.
α
l
h
30
1 : 1
典例精析
例4、 如图,一山坡的坡度为i=1:2.小王从山脚A出发, 沿山坡向上走了240m到达点C.这座山坡的坡角是多少度?小刚上升了多少米(角度精确到0.01°,长度精确到0.1m)?
A
C
i=1:2
典例精析
解:用α表示坡角的大小,由题意可得
tanα= ,
2
1
因此 α≈26.57°.
∠B=90°,∠A=26.57°,AC=240m,
在Rt△ABC中,
因此sinα= = .
AC
BC
240
BC
BC=240×sin26.57°≈107.3(m).
答:这座山坡的坡角约为26.57°,小王上升了约107.3 m.
趁热打铁
1、如图,拦水坝的横截面是梯形ABCD,AF=DE=6m,斜坡AB的坡度i=1∶1.52,斜坡CD的坡度i=1∶3,求:
(1) 坡角α 和β的度数(精确到 1°);
A
D
B
C
i=1:3
6m
β
i=1:1.5
解: 斜坡CD的坡度i = tanβ = 1 : 3,
由计算器可算得α≈33°.
α
E
F
斜坡AB的坡度i = tanα = 1 : 1.5,
由计算器可算得α≈18°.
趁热打铁
解:由题意可知 AF=DE=6m.
在Rt△ABF中,
(2) 斜坡AB的长度 (精确到0.1m).
A
D
B
C
i=1:3
β
i=1:1.5
α
E
F
6m
在Rt△ABF中,由勾股定理可得:
故斜坡AB的长度为10.8m.
归纳总结
利用解直角三角形解决简单问题的一般解题步骤:
1. 将实际问题抽象为数学问题;
2. 根据条件的特点,适当选用锐角三角函数等去解直角三角形;
3. 得到数学问题的答案;
4. 得到实际问题的答案.
综合演练
1、如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )
A. 250米
B. 米
C. 米
D. 米
A
综合演练
2、如图,某山坡的坡面AB=200米,坡角∠BAC=30°,则该山坡的坡度为( )
A.1:4 B. 1:2 C.1:3 D. 1:
D
综合演练
3.小亮为测量如图所示的湖面的宽度BC,他在同一水平面上取一点A,测得湖的一端C在A处的正北方向,另一端B在A处的北偏东60°的方向,并测得A,C间的距离AC=10 m,则湖的宽度BC为________m.
综合演练
4. 如图,某渔船如图所示,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需的时间是 .
15分钟
综合演练
5.如图有一个古镇建筑A,它周围800米内有古建筑,乡村路要由西向东修筑,在B点处测得古建筑A在北偏东60°方向上,向前直行1200米到达D点,这时 测得古建筑A在D点北偏东30°方向上,如果不改变修筑的方向,你认为古建筑会不会遭到破坏?
综合演练
解:过点A作AE垂直于BD,垂足为E.
∵点A处在B点的北偏东60°方向上,
∴∠ABE=30°.
又∵A在D点的北偏东30°方向上,
∴∠ADE=60°.
∴∠BAD=∠ADE -∠ABE=30°=∠ABE.
∴BD=AD=1200米,
∴DE=ADcos60°=600(米),
AE=600 ≈1039.2>800(米).∴不会遭到破坏.
课堂总结
说一说如何用方位角、坡度解决有关的实际问题?
本节课你有哪些收获?
作业布置
习题28. 2 P78页:5、11
https://www.21cnjy.com/help/help_extract.php
28.2.2应用举例
---第2课时
人教版 九年级下
教学目标
1. 正确理解方向角、坡度的概念. (重点)
2. 能运用解直角三角形知识解决方向角、坡度的问题;进一步提
高运用解直角三角形知识分析解决问题的综合能力.
(重点、难点)
情境导入
试一试:观察下图中图形的方位,试着描述它们的位置。
小岛
轮船
渔船
灯
塔
东
北
回顾旧知
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于90°的角,叫做方位角. 如图所示:
方位角:
45°
45°
西南
O
东北
东
西
北
南
西北
东南
典例精析
例3、如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔 80 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(结果取整数)?
65°
34°
P
B
C
A
典例精析
解:如图 ,在Rt△APC中,
PC=PA·cos(90°-65°)
=80×cos25°
≈72.505.
在Rt△BPC中,∠B=34°,
因此,当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130n mile.
65°
34°
P
B
C
A
趁热打铁
1、如图,海岛A的周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在点B处测得海岛A位于北偏东60°,航行12海里到达点D处,又测得海岛A位于北偏东30°,如果渔船不改变航向继续向东航行,有没有触礁的危险?
解:过A作AF⊥BD于点F,
则AF的长是A到BC的最短距离.
∵BC∥DE∥AF,
∴∠CBA=∠BAF=60°,
∠ADE=∠DAF=30°,
∴∠BAD=∠BAF-∠DAF=30°.
北
东
A
D
B
60°
30°
C
E
F
趁热打铁
又∵∠ABD =∠CBF-∠CBA
= 90°-60°=30°=∠BAD,
∴BD=AD=12海里,
∴AF=AD · cos30°=6 (海里),
6 ≈10.392>8,
故渔船继续向正东方向行驶,没有触礁的危险.
北
东
A
D
B
60°
30°
C
E
F
合作探究
思考1:如图,从山脚到山顶有两条路AB与BC,问哪条路比较陡?
思考2:如何用数量来刻画哪条路陡呢?
A
B
C
BC
合作探究
α
l
h
1. 坡角
坡面与水平面的夹角叫做坡角,记作 α .
2. 坡度 (或坡比)
温馨提示:坡度通常写成 1∶m的形式,如i=1∶6.
如图所示,坡面的铅垂高度 (h) 和水
平长度 (l) 的比叫做坡面的坡度
(或坡比),记作i, 即 i = h : l .
坡面
水平面
3. 坡度与坡角的关系
即坡度等于坡角的正切值.
趁热打铁
1. 斜坡的坡度是 ,则坡角α =___度.
2. 斜坡的坡角是45° ,则坡比是 _____.
3. 斜坡长是12米,坡高6米,则坡比是_______.
α
l
h
30
1 : 1
典例精析
例4、 如图,一山坡的坡度为i=1:2.小王从山脚A出发, 沿山坡向上走了240m到达点C.这座山坡的坡角是多少度?小刚上升了多少米(角度精确到0.01°,长度精确到0.1m)?
A
C
i=1:2
典例精析
解:用α表示坡角的大小,由题意可得
tanα= ,
2
1
因此 α≈26.57°.
∠B=90°,∠A=26.57°,AC=240m,
在Rt△ABC中,
因此sinα= = .
AC
BC
240
BC
BC=240×sin26.57°≈107.3(m).
答:这座山坡的坡角约为26.57°,小王上升了约107.3 m.
趁热打铁
1、如图,拦水坝的横截面是梯形ABCD,AF=DE=6m,斜坡AB的坡度i=1∶1.52,斜坡CD的坡度i=1∶3,求:
(1) 坡角α 和β的度数(精确到 1°);
A
D
B
C
i=1:3
6m
β
i=1:1.5
解: 斜坡CD的坡度i = tanβ = 1 : 3,
由计算器可算得α≈33°.
α
E
F
斜坡AB的坡度i = tanα = 1 : 1.5,
由计算器可算得α≈18°.
趁热打铁
解:由题意可知 AF=DE=6m.
在Rt△ABF中,
(2) 斜坡AB的长度 (精确到0.1m).
A
D
B
C
i=1:3
β
i=1:1.5
α
E
F
6m
在Rt△ABF中,由勾股定理可得:
故斜坡AB的长度为10.8m.
归纳总结
利用解直角三角形解决简单问题的一般解题步骤:
1. 将实际问题抽象为数学问题;
2. 根据条件的特点,适当选用锐角三角函数等去解直角三角形;
3. 得到数学问题的答案;
4. 得到实际问题的答案.
综合演练
1、如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )
A. 250米
B. 米
C. 米
D. 米
A
综合演练
2、如图,某山坡的坡面AB=200米,坡角∠BAC=30°,则该山坡的坡度为( )
A.1:4 B. 1:2 C.1:3 D. 1:
D
综合演练
3.小亮为测量如图所示的湖面的宽度BC,他在同一水平面上取一点A,测得湖的一端C在A处的正北方向,另一端B在A处的北偏东60°的方向,并测得A,C间的距离AC=10 m,则湖的宽度BC为________m.
综合演练
4. 如图,某渔船如图所示,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需的时间是 .
15分钟
综合演练
5.如图有一个古镇建筑A,它周围800米内有古建筑,乡村路要由西向东修筑,在B点处测得古建筑A在北偏东60°方向上,向前直行1200米到达D点,这时 测得古建筑A在D点北偏东30°方向上,如果不改变修筑的方向,你认为古建筑会不会遭到破坏?
综合演练
解:过点A作AE垂直于BD,垂足为E.
∵点A处在B点的北偏东60°方向上,
∴∠ABE=30°.
又∵A在D点的北偏东30°方向上,
∴∠ADE=60°.
∴∠BAD=∠ADE -∠ABE=30°=∠ABE.
∴BD=AD=1200米,
∴DE=ADcos60°=600(米),
AE=600 ≈1039.2>800(米).∴不会遭到破坏.
课堂总结
说一说如何用方位角、坡度解决有关的实际问题?
本节课你有哪些收获?
作业布置
习题28. 2 P78页:5、11
https://www.21cnjy.com/help/help_extract.php
