4.2.1 直线、射线和线段的概念和表示 课件(共28张PPT)
文档属性
| 名称 | 4.2.1 直线、射线和线段的概念和表示 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 13:42:35 | ||
图片预览






文档简介
(共28张PPT)
第四章 几何图形初步
4.2 第1课时 直线、射线和线段的概念和表示
随堂演练
课堂小结
例题讲解
知识回顾
获取新知
知识回顾
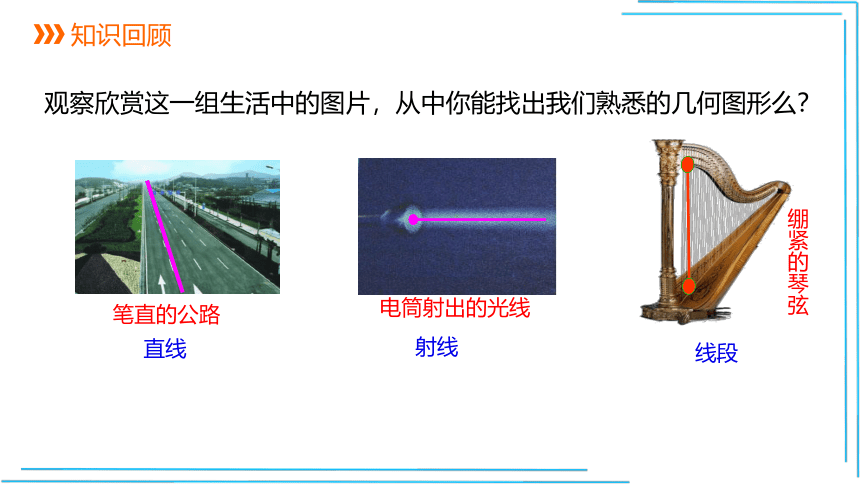
电筒射出的光线
笔直的公路
绷紧的琴弦
射线
直线
线段
观察欣赏这一组生活中的图片,从中你能找出我们熟悉的几何图形么?
获取新知
游戏大比拼
游戏规则:两位同学一组,在草稿纸上先画一个点,两位同学都经过这个点画不同的直线,甲先乙后,谁在纸上画不出新的直线谁就输了。
游戏结果说明了什么?
经过一点有无数条直线。
·
游戏规则:两位同学一组,在草稿纸上先画两个点,两位同学都经过这两个点画不同的直线,甲先乙后,谁在纸上画不出新的直线谁就输了。
·
·
A
B
游戏结果说明了什么?
经过两点有一条直线,并且只有一条直线。
简述为:两点确定一条直线。
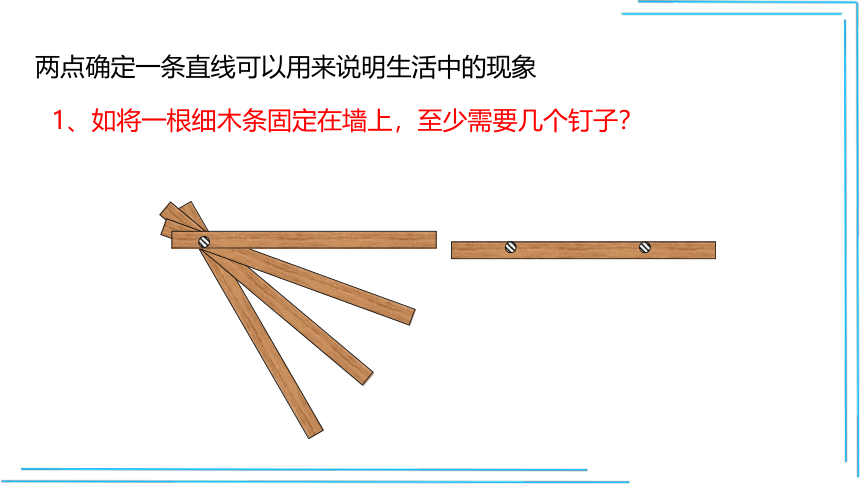
1、如将一根细木条固定在墙上,至少需要几个钉子?
两点确定一条直线可以用来说明生活中的现象
2. 建筑工人砌墙时,会在两个墙角的位置分别插 一根木桩,然后拉一条直的参考线.
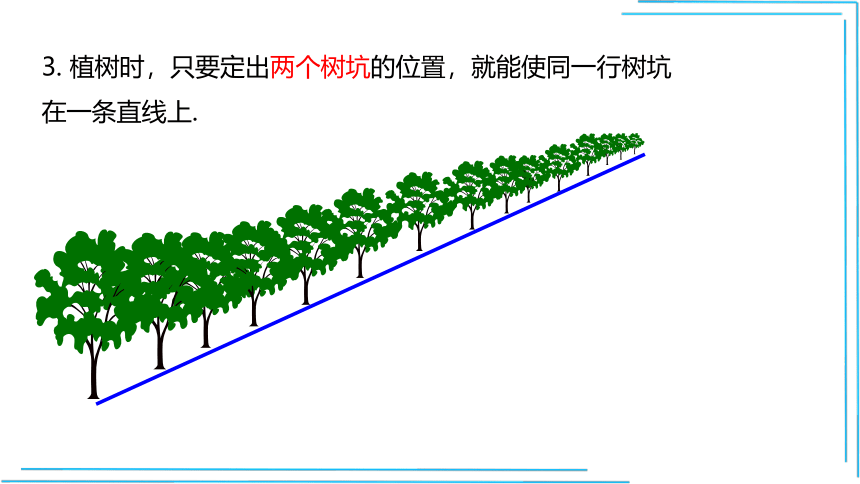
3. 植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上.
4.射击的时候,你知道是如何瞄准目标的吗?
表示直线的方法
①用一个小写字母表示,如直线 l;
②用两个大写字母表示,注:这两个大写字母可交换顺序.
A
B
l
直线 l、直线 AB、直线BA
点与直线的位置关系:
一个点在直线上,也可以说直线经过这个点;
一个点在直线外,也可以说直线不经过这个点.
· o
l
· o
l
点O在直线l外
点O在直线l上
直线l经过点O
直线l不经过点O
直线a和b相交于点O.
a
b
当两条不同的直线有一个公共点时,我们称这两条直线相交,这个公共点叫做它们的交点.
两直线相交,只有一个交点.
·
o
线段
射线
直线
A
B
a
O
A
线段 AB 线段 BA 线段 a
射线 OA 射线 l
直线 MN 直线 NM 直线 l
端点字母必须写在前面
l
M
N
l
备注:线段和射线都是直线的一部分.
线段、射线、直线的区别与联系
类型 端点数 可否延伸 可否度量
线段
射线
直线
2个
不能延伸
可度量
1个
向一个方向无限延伸
不可度量
无端点
向两个方向无限延伸
不可度量
线段: ①用两个端点的字母来表示,无先后顺序.
②用一个小写字母表示.
射线: ① 用端点及射线上一点来表示,注意端点的字母写在前面.
②用一个小写字母表示.
直线: ①用直线上两个点来表示,无先后顺序.
②用一个小写字母来表示.
例1 图中共有几条线段?
导引:以A为左端点的线段有:线段AC、线段AD、 线段AB,
以C为左端点的线段有:线段CD、 线段CB,
以D为左端点的线段有:线段DB.
解:共有6条线段.
顺序数,勿遗漏,勿重复,即有序数数法.
例题讲解
例2 按语句画图:
2、点A在直线a外;
3、经过点O的三条线段a、b、c;
4、线段AB、CD相交于点B。
1、直线EF经过点C;
E
F
C
a
A
a
b
c
O
A
B
C
D
例3 已知同一平面内有M,N,O,P四个点,请画图并回答:经过四个点中的任意两个点共能画多少条直线?
解:(1)如图①,四个点都在同一直线上,这种情况下只能画一条直线.
(2)如图②, 有三点在同一直线上,这种情况下能画四条直线.
(3)如图③,任意三点都不在同一直线上,这种情况下能画六条直线.
随堂演练
1. 在同一平面内有三个点A,B,C,过其中任意两个点做直线,可以画出的直线的条数是( )
A. 1 B. 2 C. 1或3 D. 无法确定
C
2. 下列语句准确规范的是 ( )
A. 延长直线AB B. 直线AB,CD相交于点M
C. 延长射线 AO 到点B D. 直线 a,b 相交于一点m
B
3. 下列几何语言描述正确的是( )
A.直线mn与直线ab相交于点D
B.点A在直线M上
C.点A在直线AB上
D.延长直线AB
C
4. 如图,直线的表示方法( )
A.都正确
B.都错误
C.只有一个错误
D.只有一个正确
D
5. 用一个钉子把一根细木条钉在木板上,用手拨木条,木条能转动,这说明____________________________,用两个钉子把细木条钉在木板上,就能固定细木条,这说明____________________.
经过一点可以画无数条直线
两点确定一条直线
6. 如图,A,B,C三点在一条直线上,
(1) 图中有几条直线,怎样表示它们?
(2) 图中有几条线段,怎样表示它们?
(3) 射线 AB 和射线 AC 是同一条射线吗?
(4) 图中有几条射线?写出以点B为端点的射线.
A
B
C
解:(1) 1条,直线AB或直线AC或直线BC;
(2) 3条,线段AB,线段BC,线段AC;
(3) 是;
(4) 6条.以B为端点的射线有射线BC、射线BA.
7.往返于A、B两地的客车,中途停靠三个站,每两站间的票价均不相同,问:
(1)有多少种不同的票价?
(2)要准备多少种车票?
解:画出示意图如下:
A
C
D
E
B
(1)图中一共有10条线段,故有10种不同的票价.
(2)来回的车票不同,故有10×2=20(种)不同的车票.
课堂小结
直线、射线、线段
基本事实
表示方法
两点确定一条直线
用一个小写字母表示
用两个大写字母表示
联系与区别
点与直线的位置关系
点在直线上
点在直线外
线段和射线都是直线的一部分.
https://www.21cnjy.com/help/help_extract.php
第四章 几何图形初步
4.2 第1课时 直线、射线和线段的概念和表示
随堂演练
课堂小结
例题讲解
知识回顾
获取新知
知识回顾
电筒射出的光线
笔直的公路
绷紧的琴弦
射线
直线
线段
观察欣赏这一组生活中的图片,从中你能找出我们熟悉的几何图形么?
获取新知
游戏大比拼
游戏规则:两位同学一组,在草稿纸上先画一个点,两位同学都经过这个点画不同的直线,甲先乙后,谁在纸上画不出新的直线谁就输了。
游戏结果说明了什么?
经过一点有无数条直线。
·
游戏规则:两位同学一组,在草稿纸上先画两个点,两位同学都经过这两个点画不同的直线,甲先乙后,谁在纸上画不出新的直线谁就输了。
·
·
A
B
游戏结果说明了什么?
经过两点有一条直线,并且只有一条直线。
简述为:两点确定一条直线。
1、如将一根细木条固定在墙上,至少需要几个钉子?
两点确定一条直线可以用来说明生活中的现象
2. 建筑工人砌墙时,会在两个墙角的位置分别插 一根木桩,然后拉一条直的参考线.
3. 植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上.
4.射击的时候,你知道是如何瞄准目标的吗?
表示直线的方法
①用一个小写字母表示,如直线 l;
②用两个大写字母表示,注:这两个大写字母可交换顺序.
A
B
l
直线 l、直线 AB、直线BA
点与直线的位置关系:
一个点在直线上,也可以说直线经过这个点;
一个点在直线外,也可以说直线不经过这个点.
· o
l
· o
l
点O在直线l外
点O在直线l上
直线l经过点O
直线l不经过点O
直线a和b相交于点O.
a
b
当两条不同的直线有一个公共点时,我们称这两条直线相交,这个公共点叫做它们的交点.
两直线相交,只有一个交点.
·
o
线段
射线
直线
A
B
a
O
A
线段 AB 线段 BA 线段 a
射线 OA 射线 l
直线 MN 直线 NM 直线 l
端点字母必须写在前面
l
M
N
l
备注:线段和射线都是直线的一部分.
线段、射线、直线的区别与联系
类型 端点数 可否延伸 可否度量
线段
射线
直线
2个
不能延伸
可度量
1个
向一个方向无限延伸
不可度量
无端点
向两个方向无限延伸
不可度量
线段: ①用两个端点的字母来表示,无先后顺序.
②用一个小写字母表示.
射线: ① 用端点及射线上一点来表示,注意端点的字母写在前面.
②用一个小写字母表示.
直线: ①用直线上两个点来表示,无先后顺序.
②用一个小写字母来表示.
例1 图中共有几条线段?
导引:以A为左端点的线段有:线段AC、线段AD、 线段AB,
以C为左端点的线段有:线段CD、 线段CB,
以D为左端点的线段有:线段DB.
解:共有6条线段.
顺序数,勿遗漏,勿重复,即有序数数法.
例题讲解
例2 按语句画图:
2、点A在直线a外;
3、经过点O的三条线段a、b、c;
4、线段AB、CD相交于点B。
1、直线EF经过点C;
E
F
C
a
A
a
b
c
O
A
B
C
D
例3 已知同一平面内有M,N,O,P四个点,请画图并回答:经过四个点中的任意两个点共能画多少条直线?
解:(1)如图①,四个点都在同一直线上,这种情况下只能画一条直线.
(2)如图②, 有三点在同一直线上,这种情况下能画四条直线.
(3)如图③,任意三点都不在同一直线上,这种情况下能画六条直线.
随堂演练
1. 在同一平面内有三个点A,B,C,过其中任意两个点做直线,可以画出的直线的条数是( )
A. 1 B. 2 C. 1或3 D. 无法确定
C
2. 下列语句准确规范的是 ( )
A. 延长直线AB B. 直线AB,CD相交于点M
C. 延长射线 AO 到点B D. 直线 a,b 相交于一点m
B
3. 下列几何语言描述正确的是( )
A.直线mn与直线ab相交于点D
B.点A在直线M上
C.点A在直线AB上
D.延长直线AB
C
4. 如图,直线的表示方法( )
A.都正确
B.都错误
C.只有一个错误
D.只有一个正确
D
5. 用一个钉子把一根细木条钉在木板上,用手拨木条,木条能转动,这说明____________________________,用两个钉子把细木条钉在木板上,就能固定细木条,这说明____________________.
经过一点可以画无数条直线
两点确定一条直线
6. 如图,A,B,C三点在一条直线上,
(1) 图中有几条直线,怎样表示它们?
(2) 图中有几条线段,怎样表示它们?
(3) 射线 AB 和射线 AC 是同一条射线吗?
(4) 图中有几条射线?写出以点B为端点的射线.
A
B
C
解:(1) 1条,直线AB或直线AC或直线BC;
(2) 3条,线段AB,线段BC,线段AC;
(3) 是;
(4) 6条.以B为端点的射线有射线BC、射线BA.
7.往返于A、B两地的客车,中途停靠三个站,每两站间的票价均不相同,问:
(1)有多少种不同的票价?
(2)要准备多少种车票?
解:画出示意图如下:
A
C
D
E
B
(1)图中一共有10条线段,故有10种不同的票价.
(2)来回的车票不同,故有10×2=20(种)不同的车票.
课堂小结
直线、射线、线段
基本事实
表示方法
两点确定一条直线
用一个小写字母表示
用两个大写字母表示
联系与区别
点与直线的位置关系
点在直线上
点在直线外
线段和射线都是直线的一部分.
https://www.21cnjy.com/help/help_extract.php
