九年级2012-2013学年度第一学期第一次月考数学试题
文档属性
| 名称 | 九年级2012-2013学年度第一学期第一次月考数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 145.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-28 00:00:00 | ||
图片预览



文档简介
2012-2013学年度第一学期第一次月考数学试题
一、选择题(40分)
1.下列函数中,能表示y是x的二次函数的是( )
A. B. C. y2 =2x-1 D. y=x(3x-1) -3x
2. 下列函数中,当x>0 时y值随x值增大而减小的是( ).
A.y = x2 B.y = x﹣1 C. y =- x D.y = -
3. 关于反比例函数的图象,下列说法正确的是( )
A.必经过点(1,1) B.两个分支分布在第二、四象限 C.两个分支关于x轴成轴对称 D.两个分支关于原点成中心对称
4. 小明乘车从安庆到合肥,行车的平均速度y(km/h)和行车时间x(h)之间的函数图像是( )
A B C D
5.抛物线可以由抛物线平移得到,则下列平移过程正确的是( )
A.先向右平移2个单位,再向上平移3个单位
B.先向左平移2个单位,再向下平移3个单位
C.先向右平移2个单位,再向下平移3个单位
D.先向左平移2个单位,再向上平移3个单位。
6.若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
x -7 -6 -5 -4 -3 -2
y -27 -13 -3 3 5 3
则当x=1时,y的值为
A.5 B.-3 C.-13 D.-27
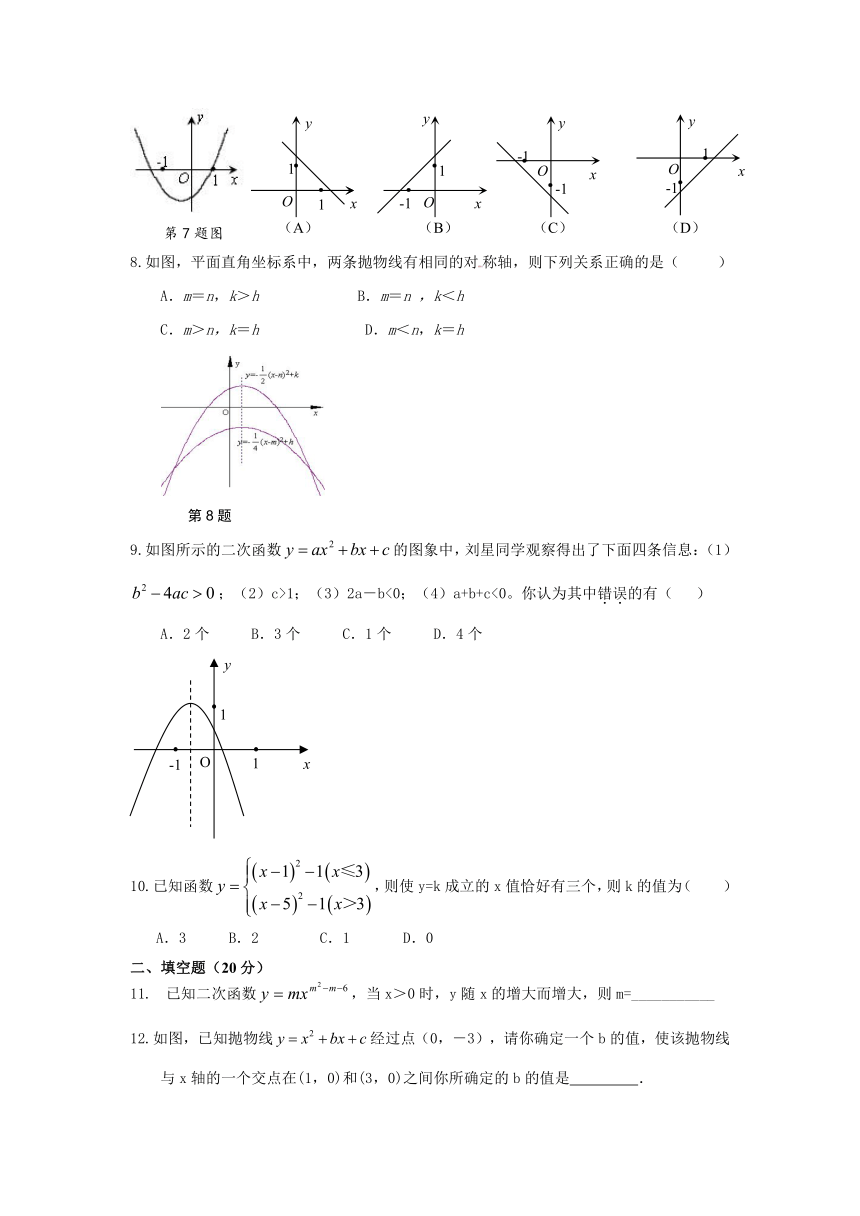
7.已知函数(其中)的图象如下面右图所示,则函数的图象可能正确的是( )
8.如图,平面直角坐标系中,两条抛物线有相同的对称轴,则下列关系正确的是( )
A.m=n,k>h B.m=n ,k<h
C.m>n,k=h D.m<n,k=h
第8题
9.如图所示的二次函数的图象中,刘星同学观察得出了下面四条信息:(1);(2)c>1;(3)2a-b<0;(4)a+b+c<0。你认为其中错误的有( )
A.2个 B.3个 C.1个 D.4个
10.已知函数,则使y=k成立的x值恰好有三个,则k的值为( )
A.3 B.2 C.1 D.0
二、填空题(20分)
11.已知二次函数,当x>0时,y随x的增大而增大,则m=___________
12.如图,已知抛物线经过点(0,-3),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间你所确定的b的值是 .
13. 如图,点A在双曲线上,点B在双曲线上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为 .
14.给出下列命题:
命题1.点(1,1)是双曲线与抛物线的一个交点.
命题2.点(1,2)是双曲线与抛物线的一个交 点.
命题3.点(1,3)是双曲线与抛物线的一个交点.
……
请你观察上面的命题,猜想出命题(是正整数):
三、(本大题共2小题,每小题8分,满分16分)
15.如图,已知直线经过点P(,),点P关于轴的对称点P′在反比例函数()的图象上.
(1)求的值;
(2)直接写出点P′的坐标;
(3)求反比例函数的解析式.
16.已知一次函数与反比例函数,其中一次函数的图象经过点P(,5).
①试确定反比例函数的表达式;
②若点Q是上述一次函数与反比例函数图象在第三象限的交点,求点Q的坐标
四、(本大题共2小题,每小题8分,满分16分)
17.已知抛物线与x轴有交点.
(1)求c的取值范围;
(2)试确定直线y=cx+l经过的象限,并说明理由.
18.张大爷要围成一个矩形花圃。花圃的一边利用足够长的墙,另三边用总长32米的篱笆恰好围成。设矩形与墙平行的一边长为x米,矩形的面积为S平方米。
(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当x为何值时,S有最大值?并求出最大值。
五(本大题共2小题,每小题10分,满分20分)
19已知二次函数y = - x2 - x + .
(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y < 0时,x的取值范围;
(3)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式.
20已知:关于x的方程
求当a取何值时,二次函数的对称轴是x=-2;
求证:a取任何实数时,方程总有实数根.
六、(本题满分12分)
21.如图,在直角坐标系中,O为坐标原点. 已知反比例函数
(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为 .
(1)求k和m的值;
(2)点C(x,y)在反比例函数y= 的图象上,求当1≤x≤3时函数值y的取值范围;
(3)过原点O的直线l与反比例函数y= 的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
七、(本题满分12分)
22某商场试销一种成本为60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量(件)与销售单价(元)符合一次函数y=kx+b,且x=65时,y=55,x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元
(3)若该商场获得利润不低于500元,是确定销售单价x的范围。
八、(本题满分14分)
23.如图,抛物线y=x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
⑴求抛物线的解析式及顶点D的坐标;
⑵判断△ABC的形状,证明你的结论;
⑶点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.
参考答案
1-10 BCDBA DDACA
11 3. 12 (答案不唯一). 13 2.
14 点(1,n)是双曲线与抛物线的一个交点
15(1)将P(-2,a)代入得a=-2×(-2)=4;
(2) P′(2,4)
(3)将P′(2,4)代入得4=,解得k=8,∴反比例函数的解析式为.
16 解:因一次函数y=x+2的图象经过点P(k,5),
所以得5=k+2,解得k=3
所以反比例函数的表达式为
(2)联立得方程组
解得 或
故第三象限的交点Q的坐标为(-3,-1)
17(1)∵抛物线与x轴没有交点
∴⊿<0,即1-2c<0
解得c>
(2)∵c>
∴直线y=x+1随x的增大而增大,
∵b=1
∴直线y=x+1经过第一、二、三象限
18 (1) 由题意得S=x(32-2x), ∴S=-2x2+32x (2)∵a=-2<0,∴S有最大值
且当x=时,S最大值 =
19(1)略;
(2)当y < 0时,x的取值范围是x<-3或x>1;
(3)平移后图象所对应的函数关系式为y=- (x-2)2+2(或写成y=- x2+2x).
20(1)解:∵二次函数的对称轴是x=-2
∴
解得a=-1
经检验a=-1是原分式方程的解.
所以a=-1时,二次函数的对称轴是x=-2;
(2)1)当a=0时,原方程变为-x-1=0,方程的解为x= -1;
2)当a≠0时,原方程为一元二次方程,,
当方程总有实数根,
∴
整理得,
∵a≠0时 总成立
所以a取任何实数时,方程总有实数根.
21(1)∵A(2,m) ∴OB=2 AB=m
∴S△AOB= OB AB=×2×m= ∴m=
∴点A的坐标为(2,) 把A(2,)代入y=,得=
∴k=1
(2)∵当x=1时,y=1;当x=3时,y=
又 ∵反比例函数y=在x>0时,y随x的增大而减小,
∴当1≤x≤3时,y的取值范围为≤y≤1。
(3) 由图象可得,线段PQ长度的最小值为2。
22 (1)根据题意,得 解得k=-1,b=120. 又
故60≤x≤87.所以所求一次函数的表达式为y=-x+120(60≤x≤87)
(2)W=(x-60)(-x+120)=-x2+180x-7200=-(x-90)2+900 因为抛物线的开口向下,所以当x<90时,W随x的增大而增大,而60≤x≤87 所以当x=87时,W最大=-(87-90)2+900=891(元)
(3)由W=500,得-x2+180x-7200=500 解得x1=70, x2=110 即要使商场可获得不低于500元利润 ,销售单价应在70至110元之间,而60≤x≤87,所以销售单价的范围是70≤x≤87
23(1)∵点A(-1,0)在抛物线y=x2 + bx-2上,∴× (-1 )2 + b× (-1) –2 = 0,解得b =
∴抛物线的解析式为y=x2-x-2. y=x2-x-2 = ( x2 -3x- 4 ) =(x-)2-,
∴顶点D的坐标为 (, -).
(2)当x = 0时y = -2, ∴C(0,-2),OC = 2。
当y = 0时, x2-x-2 = 0, ∴x1 = -1, x2 = 4, ∴B (4,0)
∴OA = 1, OB = 4, AB = 5.
∵AB2 = 25, AC2 = OA2 + OC2 = 5, BC2 = OC2 + OB2 = 20,
∴AC2 +BC2 = AB2. ∴△ABC是直角三角形.
(3)作出点C关于x轴的对称点C′,则C′(0,2),OC′=2,连接C′D交x轴于点M,根据轴对称性及两点之间线段最短可知,MC + MD的值最小。
设直线C′D的解析式为y = kx + n ,
则,解得n = 2, .
∴ .
∴当y = 0时, ,
. ∴.
第7题图
y
x
1
1
O
(A)
y
x
1
-1
O
(B)
y
x
-1
-1
O
(C)
1
-1
x
y
O
(D)
x
y
-1
1
O
1
第15题
x
y
O
P
B
O
A
第23题图
一、选择题(40分)
1.下列函数中,能表示y是x的二次函数的是( )
A. B. C. y2 =2x-1 D. y=x(3x-1) -3x
2. 下列函数中,当x>0 时y值随x值增大而减小的是( ).
A.y = x2 B.y = x﹣1 C. y =- x D.y = -
3. 关于反比例函数的图象,下列说法正确的是( )
A.必经过点(1,1) B.两个分支分布在第二、四象限 C.两个分支关于x轴成轴对称 D.两个分支关于原点成中心对称
4. 小明乘车从安庆到合肥,行车的平均速度y(km/h)和行车时间x(h)之间的函数图像是( )
A B C D
5.抛物线可以由抛物线平移得到,则下列平移过程正确的是( )
A.先向右平移2个单位,再向上平移3个单位
B.先向左平移2个单位,再向下平移3个单位
C.先向右平移2个单位,再向下平移3个单位
D.先向左平移2个单位,再向上平移3个单位。
6.若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
x -7 -6 -5 -4 -3 -2
y -27 -13 -3 3 5 3
则当x=1时,y的值为
A.5 B.-3 C.-13 D.-27
7.已知函数(其中)的图象如下面右图所示,则函数的图象可能正确的是( )
8.如图,平面直角坐标系中,两条抛物线有相同的对称轴,则下列关系正确的是( )
A.m=n,k>h B.m=n ,k<h
C.m>n,k=h D.m<n,k=h
第8题
9.如图所示的二次函数的图象中,刘星同学观察得出了下面四条信息:(1);(2)c>1;(3)2a-b<0;(4)a+b+c<0。你认为其中错误的有( )
A.2个 B.3个 C.1个 D.4个
10.已知函数,则使y=k成立的x值恰好有三个,则k的值为( )
A.3 B.2 C.1 D.0
二、填空题(20分)
11.已知二次函数,当x>0时,y随x的增大而增大,则m=___________
12.如图,已知抛物线经过点(0,-3),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间你所确定的b的值是 .
13. 如图,点A在双曲线上,点B在双曲线上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为 .
14.给出下列命题:
命题1.点(1,1)是双曲线与抛物线的一个交点.
命题2.点(1,2)是双曲线与抛物线的一个交 点.
命题3.点(1,3)是双曲线与抛物线的一个交点.
……
请你观察上面的命题,猜想出命题(是正整数):
三、(本大题共2小题,每小题8分,满分16分)
15.如图,已知直线经过点P(,),点P关于轴的对称点P′在反比例函数()的图象上.
(1)求的值;
(2)直接写出点P′的坐标;
(3)求反比例函数的解析式.
16.已知一次函数与反比例函数,其中一次函数的图象经过点P(,5).
①试确定反比例函数的表达式;
②若点Q是上述一次函数与反比例函数图象在第三象限的交点,求点Q的坐标
四、(本大题共2小题,每小题8分,满分16分)
17.已知抛物线与x轴有交点.
(1)求c的取值范围;
(2)试确定直线y=cx+l经过的象限,并说明理由.
18.张大爷要围成一个矩形花圃。花圃的一边利用足够长的墙,另三边用总长32米的篱笆恰好围成。设矩形与墙平行的一边长为x米,矩形的面积为S平方米。
(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当x为何值时,S有最大值?并求出最大值。
五(本大题共2小题,每小题10分,满分20分)
19已知二次函数y = - x2 - x + .
(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y < 0时,x的取值范围;
(3)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式.
20已知:关于x的方程
求当a取何值时,二次函数的对称轴是x=-2;
求证:a取任何实数时,方程总有实数根.
六、(本题满分12分)
21.如图,在直角坐标系中,O为坐标原点. 已知反比例函数
(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为 .
(1)求k和m的值;
(2)点C(x,y)在反比例函数y= 的图象上,求当1≤x≤3时函数值y的取值范围;
(3)过原点O的直线l与反比例函数y= 的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
七、(本题满分12分)
22某商场试销一种成本为60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量(件)与销售单价(元)符合一次函数y=kx+b,且x=65时,y=55,x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元
(3)若该商场获得利润不低于500元,是确定销售单价x的范围。
八、(本题满分14分)
23.如图,抛物线y=x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
⑴求抛物线的解析式及顶点D的坐标;
⑵判断△ABC的形状,证明你的结论;
⑶点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.
参考答案
1-10 BCDBA DDACA
11 3. 12 (答案不唯一). 13 2.
14 点(1,n)是双曲线与抛物线的一个交点
15(1)将P(-2,a)代入得a=-2×(-2)=4;
(2) P′(2,4)
(3)将P′(2,4)代入得4=,解得k=8,∴反比例函数的解析式为.
16 解:因一次函数y=x+2的图象经过点P(k,5),
所以得5=k+2,解得k=3
所以反比例函数的表达式为
(2)联立得方程组
解得 或
故第三象限的交点Q的坐标为(-3,-1)
17(1)∵抛物线与x轴没有交点
∴⊿<0,即1-2c<0
解得c>
(2)∵c>
∴直线y=x+1随x的增大而增大,
∵b=1
∴直线y=x+1经过第一、二、三象限
18 (1) 由题意得S=x(32-2x), ∴S=-2x2+32x (2)∵a=-2<0,∴S有最大值
且当x=时,S最大值 =
19(1)略;
(2)当y < 0时,x的取值范围是x<-3或x>1;
(3)平移后图象所对应的函数关系式为y=- (x-2)2+2(或写成y=- x2+2x).
20(1)解:∵二次函数的对称轴是x=-2
∴
解得a=-1
经检验a=-1是原分式方程的解.
所以a=-1时,二次函数的对称轴是x=-2;
(2)1)当a=0时,原方程变为-x-1=0,方程的解为x= -1;
2)当a≠0时,原方程为一元二次方程,,
当方程总有实数根,
∴
整理得,
∵a≠0时 总成立
所以a取任何实数时,方程总有实数根.
21(1)∵A(2,m) ∴OB=2 AB=m
∴S△AOB= OB AB=×2×m= ∴m=
∴点A的坐标为(2,) 把A(2,)代入y=,得=
∴k=1
(2)∵当x=1时,y=1;当x=3时,y=
又 ∵反比例函数y=在x>0时,y随x的增大而减小,
∴当1≤x≤3时,y的取值范围为≤y≤1。
(3) 由图象可得,线段PQ长度的最小值为2。
22 (1)根据题意,得 解得k=-1,b=120. 又
故60≤x≤87.所以所求一次函数的表达式为y=-x+120(60≤x≤87)
(2)W=(x-60)(-x+120)=-x2+180x-7200=-(x-90)2+900 因为抛物线的开口向下,所以当x<90时,W随x的增大而增大,而60≤x≤87 所以当x=87时,W最大=-(87-90)2+900=891(元)
(3)由W=500,得-x2+180x-7200=500 解得x1=70, x2=110 即要使商场可获得不低于500元利润 ,销售单价应在70至110元之间,而60≤x≤87,所以销售单价的范围是70≤x≤87
23(1)∵点A(-1,0)在抛物线y=x2 + bx-2上,∴× (-1 )2 + b× (-1) –2 = 0,解得b =
∴抛物线的解析式为y=x2-x-2. y=x2-x-2 = ( x2 -3x- 4 ) =(x-)2-,
∴顶点D的坐标为 (, -).
(2)当x = 0时y = -2, ∴C(0,-2),OC = 2。
当y = 0时, x2-x-2 = 0, ∴x1 = -1, x2 = 4, ∴B (4,0)
∴OA = 1, OB = 4, AB = 5.
∵AB2 = 25, AC2 = OA2 + OC2 = 5, BC2 = OC2 + OB2 = 20,
∴AC2 +BC2 = AB2. ∴△ABC是直角三角形.
(3)作出点C关于x轴的对称点C′,则C′(0,2),OC′=2,连接C′D交x轴于点M,根据轴对称性及两点之间线段最短可知,MC + MD的值最小。
设直线C′D的解析式为y = kx + n ,
则,解得n = 2, .
∴ .
∴当y = 0时, ,
. ∴.
第7题图
y
x
1
1
O
(A)
y
x
1
-1
O
(B)
y
x
-1
-1
O
(C)
1
-1
x
y
O
(D)
x
y
-1
1
O
1
第15题
x
y
O
P
B
O
A
第23题图
