华东师大版七上数学 5.2.3平行线的性质 课件(共16张PPT)
文档属性
| 名称 | 华东师大版七上数学 5.2.3平行线的性质 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 728.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 06:52:20 | ||
图片预览






文档简介
(共16张PPT)
60°
工人在修一条高速公路时在前方遇到一个湖泊,为了降低施工难度,他们决定绕过这个湖,如果第一个弯是左拐60°,那么第二个弯应朝什么方向拐多少度,才会不改变公路的方向?聪明的同学们,请你帮帮工人们。
你知道其中隐含什么数学道理吗?
线的位置关系
角的数量关系
判定
复习回顾
两直线平行
判定
同位角相等
内错角相等
同旁内角互补
平行线的判定方法是什么?
1、已知直线a//b,请你任意画一条截线,找出其中一组同位角,再利用量角器去测量并记录下来。
实践活动
2、数据记录:
3、从表格中的数据,观察各对同位角的数量关系,大胆的去猜想 ,试着说一说;
两条平行线被第三条直线所截,同位角相等
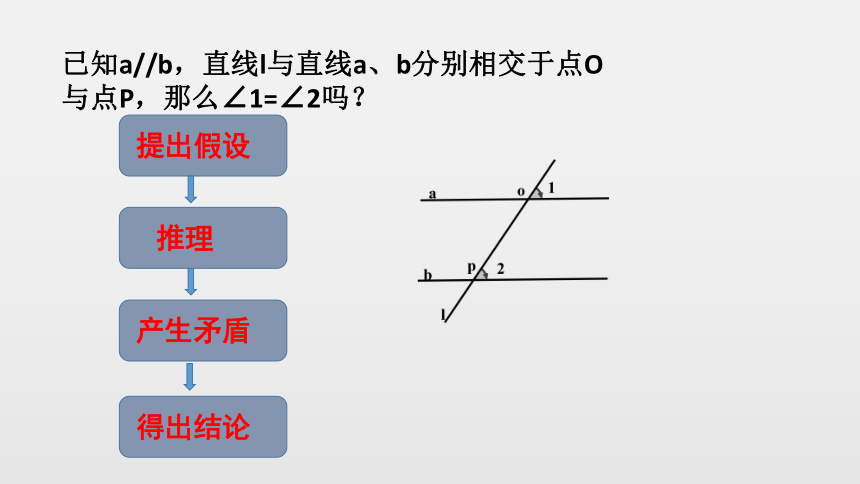
已知a//b,直线l与直线a、b分别相交于点O与点P,那么∠1=∠2吗?
提出假设
推理
产生矛盾
得出结论
两条平行线被第三条直线所截,
同位角相等.
两直线平行,同位角相等.
∴∠1=∠2.
∵a∥b,
简写为:
符号语言:
归纳总结
平行线的性质1
结论
两条平行线被第三条直线所截,
内错角相等.
两直线平行,内错角相等.
∴∠2=∠3.
∵a∥b,
简写为:
符号语言:
平行线的性质2
结论
归纳总结
已知a//b,那么∠2和∠3有什么数量关系呢?
证:∵a//b(已知)
∴∠1=∠2(两直线平行,同位角相等)
又∵∠1=∠3(已知)
∴∠2=∠3(等量代换)
两条平行线被第三条直线所截,
同旁内角互补.
两直线平行,同旁内角互补.
∴∠2+∠4=180°
∵a∥b,
简写为:
符号语言:
平行线的性质3
结论
归纳总结
已知a//b,那么∠2和∠4有什么数量关系呢?
证:∵a//b(已知)
∴∠1=∠2(两直线平行,同位角相等)
又∵∠1+∠4=180°(邻补角定义)
∴∠2+∠4=180°(等量代换)
两直线平行
判定
平行线的判定:
平行线的性质:
角的数量关系
判定
两直线平行
同位角相等
内错角相等
同旁内角互补
性质
性质
同位角相等
内错角相等
同旁内角互补
已知
结论
线的位置关系
1、 如图,已知直线a∥b,
∠1 = 500,求∠2的度数.
a
b
l
1
2
∴∠ 2=_____ ( ).
解:∵ a∥b( ),
∴∠ ____= ∠____
( )
又∵∠ 1 = 500 ( ),
3
4
你能求出∠3、∠4的度数吗?
例题精讲
已知
两直线平行,内错角相等
等量代换
500
已知
1 2
2:如图,已知∠3 =∠4,∠1=47°,求∠2的度数?
∴∠ 2= ___
( )
解:∵ ∠3 =∠4( )
∴__∥__( )
又∵∠ 1 = 470 ( )
∴∠__=∠__( )
a b
1 2
47°
∵a//b( )
已证
60°
60°
两直线平行,同位角相等
工人在修一条高速公路时在前方遇到一个湖泊,为了降低施工难度,他们决定绕过这个湖,如果第一个弯是左拐60°,那么第二个弯应朝什么方向拐多少度,才会不改变公路的方向?聪明的同学们,请你帮帮工人们。
你知道其中隐含什么数学道理吗?
如图,已知∠1=∠2,∠2=∠3,
求证:∠4=2∠1
能力提升
证明:∵∠1=∠2(已知)
∠2=∠3(已知)
∴∠1=∠3(等量代换)
∴AB//DE(内错角相等,
两直线平行)
∵AB//DE( )
∴∠BAC=∠4(两直线平行,同位角相等)
∴∠4= 2∠1(等量代换)
已证
本节课我们有哪些收获?
平行线的性质:
1.两直线平行,同位角相等.
2.两直线平行,内错角相等.
3.两直线平行,同旁内角互补;
角的数量关系
线的位置关系
判定
性质
运用的数学思想:
类比的思想
转化的思想
60°
工人在修一条高速公路时在前方遇到一个湖泊,为了降低施工难度,他们决定绕过这个湖,如果第一个弯是左拐60°,那么第二个弯应朝什么方向拐多少度,才会不改变公路的方向?聪明的同学们,请你帮帮工人们。
你知道其中隐含什么数学道理吗?
线的位置关系
角的数量关系
判定
复习回顾
两直线平行
判定
同位角相等
内错角相等
同旁内角互补
平行线的判定方法是什么?
1、已知直线a//b,请你任意画一条截线,找出其中一组同位角,再利用量角器去测量并记录下来。
实践活动
2、数据记录:
3、从表格中的数据,观察各对同位角的数量关系,大胆的去猜想 ,试着说一说;
两条平行线被第三条直线所截,同位角相等
已知a//b,直线l与直线a、b分别相交于点O与点P,那么∠1=∠2吗?
提出假设
推理
产生矛盾
得出结论
两条平行线被第三条直线所截,
同位角相等.
两直线平行,同位角相等.
∴∠1=∠2.
∵a∥b,
简写为:
符号语言:
归纳总结
平行线的性质1
结论
两条平行线被第三条直线所截,
内错角相等.
两直线平行,内错角相等.
∴∠2=∠3.
∵a∥b,
简写为:
符号语言:
平行线的性质2
结论
归纳总结
已知a//b,那么∠2和∠3有什么数量关系呢?
证:∵a//b(已知)
∴∠1=∠2(两直线平行,同位角相等)
又∵∠1=∠3(已知)
∴∠2=∠3(等量代换)
两条平行线被第三条直线所截,
同旁内角互补.
两直线平行,同旁内角互补.
∴∠2+∠4=180°
∵a∥b,
简写为:
符号语言:
平行线的性质3
结论
归纳总结
已知a//b,那么∠2和∠4有什么数量关系呢?
证:∵a//b(已知)
∴∠1=∠2(两直线平行,同位角相等)
又∵∠1+∠4=180°(邻补角定义)
∴∠2+∠4=180°(等量代换)
两直线平行
判定
平行线的判定:
平行线的性质:
角的数量关系
判定
两直线平行
同位角相等
内错角相等
同旁内角互补
性质
性质
同位角相等
内错角相等
同旁内角互补
已知
结论
线的位置关系
1、 如图,已知直线a∥b,
∠1 = 500,求∠2的度数.
a
b
l
1
2
∴∠ 2=_____ ( ).
解:∵ a∥b( ),
∴∠ ____= ∠____
( )
又∵∠ 1 = 500 ( ),
3
4
你能求出∠3、∠4的度数吗?
例题精讲
已知
两直线平行,内错角相等
等量代换
500
已知
1 2
2:如图,已知∠3 =∠4,∠1=47°,求∠2的度数?
∴∠ 2= ___
( )
解:∵ ∠3 =∠4( )
∴__∥__( )
又∵∠ 1 = 470 ( )
∴∠__=∠__( )
a b
1 2
47°
∵a//b( )
已证
60°
60°
两直线平行,同位角相等
工人在修一条高速公路时在前方遇到一个湖泊,为了降低施工难度,他们决定绕过这个湖,如果第一个弯是左拐60°,那么第二个弯应朝什么方向拐多少度,才会不改变公路的方向?聪明的同学们,请你帮帮工人们。
你知道其中隐含什么数学道理吗?
如图,已知∠1=∠2,∠2=∠3,
求证:∠4=2∠1
能力提升
证明:∵∠1=∠2(已知)
∠2=∠3(已知)
∴∠1=∠3(等量代换)
∴AB//DE(内错角相等,
两直线平行)
∵AB//DE( )
∴∠BAC=∠4(两直线平行,同位角相等)
∴∠4= 2∠1(等量代换)
已证
本节课我们有哪些收获?
平行线的性质:
1.两直线平行,同位角相等.
2.两直线平行,内错角相等.
3.两直线平行,同旁内角互补;
角的数量关系
线的位置关系
判定
性质
运用的数学思想:
类比的思想
转化的思想
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
