一元二次方程的应用(6)
文档属性
| 名称 | 一元二次方程的应用(6) |

|
|
| 格式 | zip | ||
| 文件大小 | 222.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-28 20:01:03 | ||
图片预览



文档简介
(共11张PPT)
实验中学九年级数学备课组
路程、速度和时间三者的关系是什么?
路程=速度×时间
我们这一节课就是要利用同学们刚才所回答的“路程=速度×时间”来建立一元二次方程的数学模型,并且解决一些实际问题.
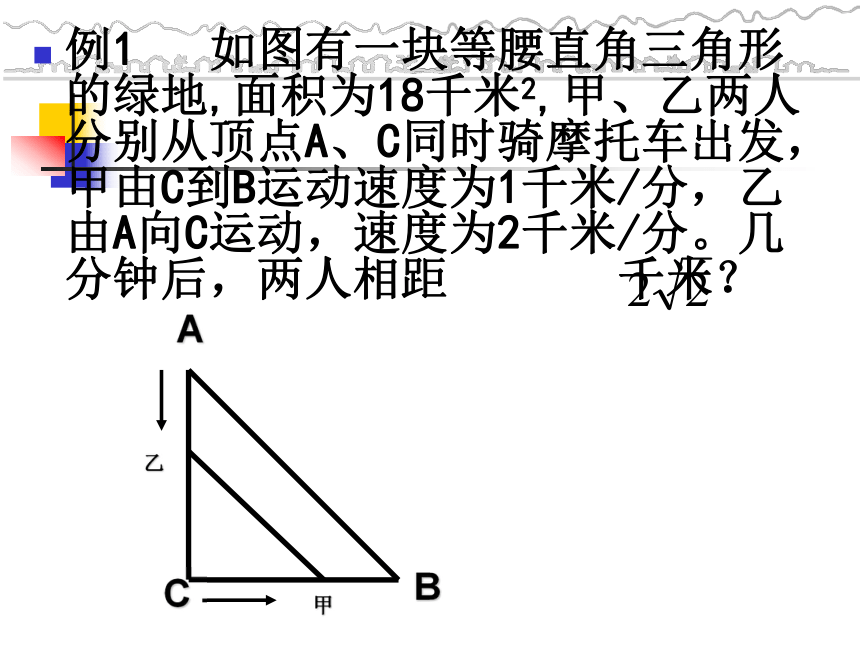
例1 如图有一块等腰直角三角形的绿地,面积为18千米2,甲、乙两人分别从顶点A、C同时骑摩托车出发,甲由C到B运动速度为1千米/分,乙由A向C运动,速度为2千米/分。几分钟后,两人相距 千米?
A
C
B
甲
乙
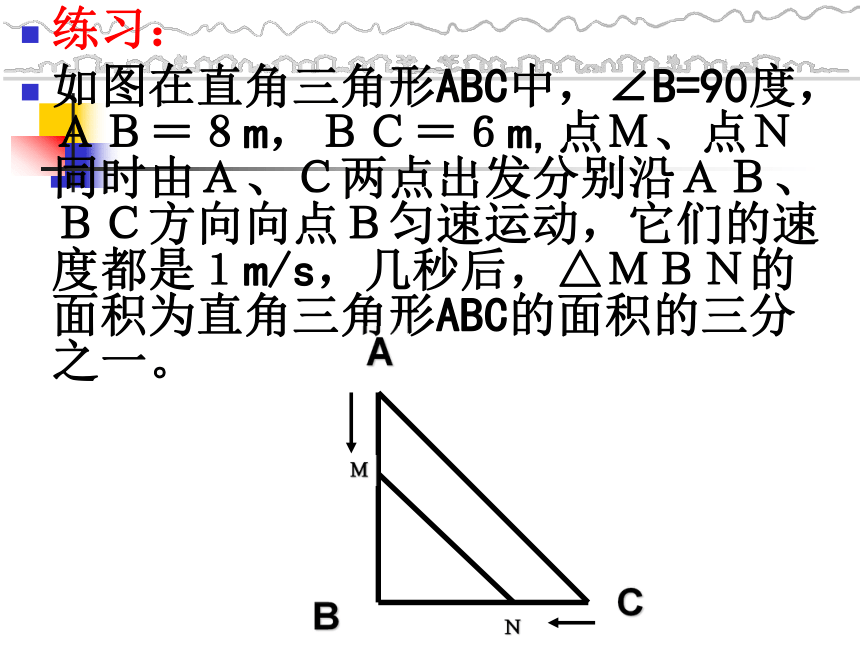
练习:
如图在直角三角形ABC中,∠B=90度,AB=8m,BC=6m,点M、点N同时由A、C两点出发分别沿AB、BC方向向点B匀速运动,它们的速度都是1m/s,几秒后,△MBN的面积为直角三角形ABC的面积的三分之一。
A
C
B
N
M
列方程解几何问题首先应根据题意正确地画出图形,结合图形及其性质列出方程求解,同时切记要检验解的合理性。
1、如图所示,已知A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到点B为止,点Q以2cm/s的速度向D移动。
问:(1)P、Q两点从出发开始几秒时,四边形PBCQ的面积是33cm2?
(2)P、Q两点从出发开始到几秒时,点P点Q间的距离是10cm?
2、如图所示,等腰Rt ABC的直角边AB=2,点P、Q分别从A、C两点同时出发,以相同速度做直线运动,已知点P沿射线AB运动,点Q沿BC的延长线运动,PQ与直线AC相交于点D。
(1)设AP的长为x,当x为何值时S△PCQ=1/4S△ABC
(2)作PE⊥AC于点E,当点P、Q运动时,线段DE的长度是否改变?证明你的结论。
[例2] 如图所示,客轮沿折线A—B—C从A出发经B再到C匀速航行,货轮从AC的中点D出发沿某一方向匀速直线航行,将一批货物送达客轮,两船同时起航,并同时到达折线A—B—C上的某点E处。已知AB=BC=200海里,∠ABC=90 ,客轮速度是货轮速度的2倍。求货物从出发到相遇共航行了多少海里?(结果保留根号)。
[例2] 如图所示,客轮沿折线A—B—C从A出发经B再到C匀速航行,货轮从AC的中点D出发沿某一方向匀速直线航行,将一批货物送达客轮,两船同时起航,并同时到达折线A—B—C上的某点E处。已知AB=BC=200海里,∠ABC=90 ,客轮速度是货轮速度的2倍。求货物从出发到相遇共航行了多少海里?(结果保留根号)。
解:因为D为AC中点。且AB=BC。所以客轮与货轮的相遇点应在BC上,过D点作DF⊥BC于F,显然E点应在BF之间,设货轮从出发到两船相遇共航行了x海里,则DE=2x,AB+BE=2x∵在等腰三角形ABC中,AB=BC=200,D是AC中点,
∴
∴DF=100,EF=300—2x 在Rt DEF中,
,
本节课应掌握:
运用路程=速度×时间,建立一元二次方程的数学模型,并解决一些实际问题.
实验中学九年级数学备课组
路程、速度和时间三者的关系是什么?
路程=速度×时间
我们这一节课就是要利用同学们刚才所回答的“路程=速度×时间”来建立一元二次方程的数学模型,并且解决一些实际问题.
例1 如图有一块等腰直角三角形的绿地,面积为18千米2,甲、乙两人分别从顶点A、C同时骑摩托车出发,甲由C到B运动速度为1千米/分,乙由A向C运动,速度为2千米/分。几分钟后,两人相距 千米?
A
C
B
甲
乙
练习:
如图在直角三角形ABC中,∠B=90度,AB=8m,BC=6m,点M、点N同时由A、C两点出发分别沿AB、BC方向向点B匀速运动,它们的速度都是1m/s,几秒后,△MBN的面积为直角三角形ABC的面积的三分之一。
A
C
B
N
M
列方程解几何问题首先应根据题意正确地画出图形,结合图形及其性质列出方程求解,同时切记要检验解的合理性。
1、如图所示,已知A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到点B为止,点Q以2cm/s的速度向D移动。
问:(1)P、Q两点从出发开始几秒时,四边形PBCQ的面积是33cm2?
(2)P、Q两点从出发开始到几秒时,点P点Q间的距离是10cm?
2、如图所示,等腰Rt ABC的直角边AB=2,点P、Q分别从A、C两点同时出发,以相同速度做直线运动,已知点P沿射线AB运动,点Q沿BC的延长线运动,PQ与直线AC相交于点D。
(1)设AP的长为x,当x为何值时S△PCQ=1/4S△ABC
(2)作PE⊥AC于点E,当点P、Q运动时,线段DE的长度是否改变?证明你的结论。
[例2] 如图所示,客轮沿折线A—B—C从A出发经B再到C匀速航行,货轮从AC的中点D出发沿某一方向匀速直线航行,将一批货物送达客轮,两船同时起航,并同时到达折线A—B—C上的某点E处。已知AB=BC=200海里,∠ABC=90 ,客轮速度是货轮速度的2倍。求货物从出发到相遇共航行了多少海里?(结果保留根号)。
[例2] 如图所示,客轮沿折线A—B—C从A出发经B再到C匀速航行,货轮从AC的中点D出发沿某一方向匀速直线航行,将一批货物送达客轮,两船同时起航,并同时到达折线A—B—C上的某点E处。已知AB=BC=200海里,∠ABC=90 ,客轮速度是货轮速度的2倍。求货物从出发到相遇共航行了多少海里?(结果保留根号)。
解:因为D为AC中点。且AB=BC。所以客轮与货轮的相遇点应在BC上,过D点作DF⊥BC于F,显然E点应在BF之间,设货轮从出发到两船相遇共航行了x海里,则DE=2x,AB+BE=2x∵在等腰三角形ABC中,AB=BC=200,D是AC中点,
∴
∴DF=100,EF=300—2x 在Rt DEF中,
,
本节课应掌握:
运用路程=速度×时间,建立一元二次方程的数学模型,并解决一些实际问题.
同课章节目录
