2021-2022学年北师大版九年级数学下册1.4解直角三角形解答题专题训练(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册1.4解直角三角形解答题专题训练(Word版,附答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 553.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-21 23:51:04 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《1.4解直角三角形》解答题专题训练(附答案)
1.(1)计算:2tan60° tan30°﹣4cos245°+sin60°;
(2)如图,在△ABC中,tanC=,点D在边BC上,AB=AD,CD=2BD=4,求sinB的值.
2.如图,在△ABC中,AB=AC=10,.求sinA的值.
3.如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,sinB=,求:
(1)线段DC的长;
(2)sin∠EDC的值.
4.如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,点D在边BC上,且BD=3CD,DE⊥AB,垂足为点E,联结CE.
(1)求线段AE的长;
(2)求∠ACE的余切值.
5.已知:BD是四边形ABCD的对角线,AB⊥BC,∠C=60°,AB=1,BC=3+,CD=2
(1)求∠ABD的值;
(2)求AD的长.
6.通过学习锐角三角比,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can),如图(1)在△ABC中,AB=AC,底角B的邻对记作canB,这时canB=,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义,解下列问题:
(1)can30°= ;
(2)如图(2),已知在△ABC中,AB=AC,canB=,S△ABC=24,求△ABC的周长.
7.已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=2,
求(1)AB的长;
(2)S△ABC.
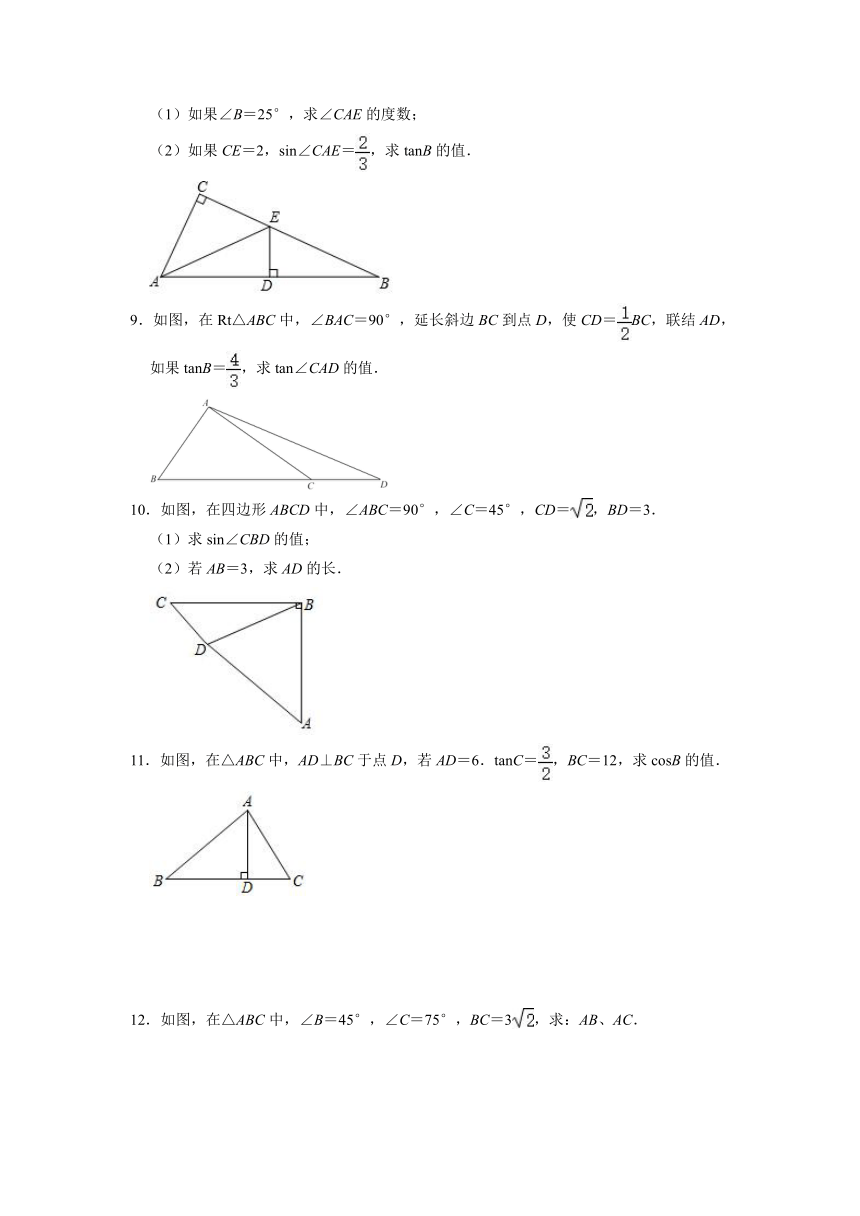
8.如图,在△ABC中,∠C=90°,AB的垂直平分线分别交边AB、BC于点D、E,连接AE.
(1)如果∠B=25°,求∠CAE的度数;
(2)如果CE=2,sin∠CAE=,求tanB的值.
9.如图,在Rt△ABC中,∠BAC=90°,延长斜边BC到点D,使CD=BC,联结AD,如果tanB=,求tan∠CAD的值.
10.如图,在四边形ABCD中,∠ABC=90°,∠C=45°,CD=,BD=3.
(1)求sin∠CBD的值;
(2)若AB=3,求AD的长.
11.如图,在△ABC中,AD⊥BC于点D,若AD=6.tanC=,BC=12,求cosB的值.
12.如图,在△ABC中,∠B=45°,∠C=75°,BC=3,求:AB、AC.
13.如图,在△ABC中,AB=AC=10,sinB=.
(1)求边BC的长度;
(2)求cosA的值.
14.如图,已知在Rt△ABC中,∠C=90°,sin∠ABC=,点D在边BC上,BD=4,联结AD,tan∠DAC=.
(1)求边AC的长;
(2)求cot∠BAD的值.
15.如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,BC=18,AD=6.
(1)求sinB的值;
(2)点E在AB上,且BE=2AE,过E作EF⊥BC,垂足为点F,求DE的长.
16.已知:如图,在Rt△ABC中,∠ACB=90°,BC=12,cosB=,D、E分别是AB、BC边上的中点,AE与CD相交于点G.
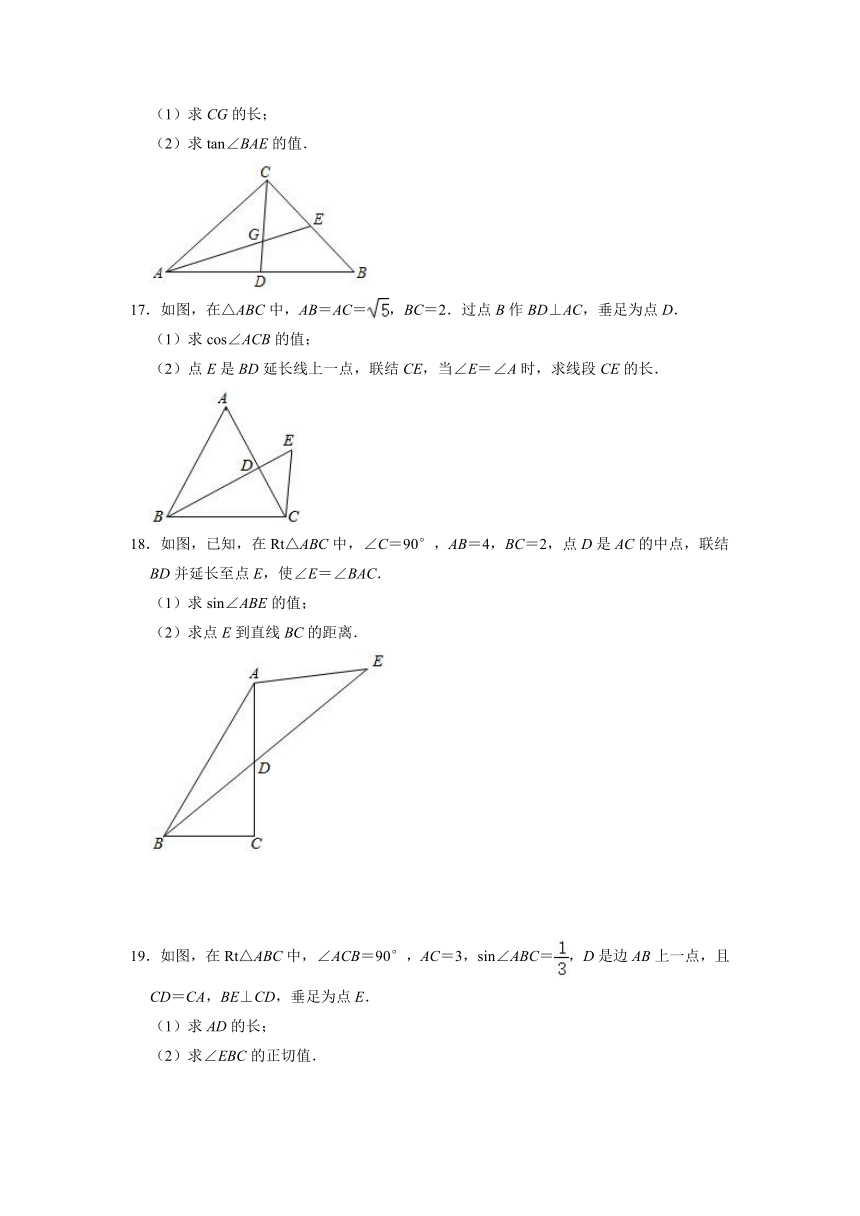
(1)求CG的长;
(2)求tan∠BAE的值.
17.如图,在△ABC中,AB=AC=,BC=2.过点B作BD⊥AC,垂足为点D.
(1)求cos∠ACB的值;
(2)点E是BD延长线上一点,联结CE,当∠E=∠A时,求线段CE的长.
18.如图,已知,在Rt△ABC中,∠C=90°,AB=4,BC=2,点D是AC的中点,联结BD并延长至点E,使∠E=∠BAC.
(1)求sin∠ABE的值;
(2)求点E到直线BC的距离.
19.如图,在Rt△ABC中,∠ACB=90°,AC=3,sin∠ABC=,D是边AB上一点,且CD=CA,BE⊥CD,垂足为点E.
(1)求AD的长;
(2)求∠EBC的正切值.
20.已知:如图,在△ABC中,AB=AC=5,BC=8,D是边AB上一点,且tan∠DCB=.
(1)试求cosB的值;
(2)试求△BCD的面积.
21.如图,在△ABC中,∠C=90°,AB的垂直平分线分别交边BC、AB于点D、E,联结AD.
(1)如果∠CAD:∠DAB=1:2,求∠CAD的度数;
(2)如果AC=1,tanB=,求∠CAD的正弦值.
22.如图,在△ABC中,AB=AC,BC=10,cos,点D是边BC的中点,点E在边AC上,且=,AD与BE相交于点F.求:
(1)边AB的长;
(2)的值.
23.如图,在Rt△ABC中,∠C=90°,点D在BC边上,∠ADC=45°,BD=2,tanB=
(1)求AC和AB的长;
(2)求sin∠BAD的值.
24.已知:如图,在△ABC中,AB=13,AC=8,cos∠BAC=,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
(1)求∠EAD的余切值;
(2)求的值.
参考答案
1.解:(1)2tan60° tan30°﹣4cos245°+sin60°
=2××﹣4×()2+
=2﹣4×+
=2﹣2+
=;
(2)作AE⊥BD于点E,
∵AB=AD,CD=2BD=4,
∴BE=DE=1,
∴CE=CD+DE=5,
∵tanC=,
∴,
∴AE=3,
∴AB===,
∴sinB=.
2.解:过点C作CD⊥AB,
在Rt△CDB中,
∵sinB==,
设CD=4x,BC=5x,
则BD=3x,
∴AD=10﹣3x,
在Rt△CDA中,由勾股定理得,
AC2=AD2+CD2,
即102=(10﹣3x)2+(4x)2,
整理得:25x2﹣60x=0,
解得:x=2.4或x=0(舍去),
∴CD=4x=9.6,
在Rt△CDA中,
sinA===.
3.解:(1)在△ABC中,∵AD是边BC上的高,
∴AD⊥BC.
∴sinB==.
∵AD=12,
∴AB===15.
在Rt△ABD中,∵BD===9,
∴CD=BC﹣BD=14﹣9=5.
(2)在Rt△ADC中,∵AD=12,DC=5,
∴AC=13.
∵E是AC的中点,
∴DE=EC,
∴∠EDC=∠C.
∴sin∠EDC=sin∠C==.
4.解:(1)∵BC=4,BD=3CD,
∴BD=3.
∵AB=BC,∠ACB=90°,
∴∠A=∠B=45°.
∵DE⊥AB,
∴在Rt△DEB中,.
∴
在Rt△ACB中,,
∴
(2)如图,过点E作EH⊥AC于点H.
∴在Rt△AHE中,,
AH=AE cos45°=,
∴,
∴EH=AH=,
∴在Rt△CHE中,cot∠ECH=,
即∠ACE的余切值是.
5.解:(1)过点D作DE⊥BC于点E,
∵在Rt△CDE 中,∠C=60°,CD=2,
∴CE=,DE=3,
∵BC=3+,
∴BE=BC﹣CE=3+﹣=3,
∴DE=BE=3,
∴在Rt△BDE 中,∠EDB=∠EBD=45°,
∵AB⊥BC,∠ABC=90°,
∴∠ABD=∠ABC﹣∠EBD=45°;
(2)过点A作AF⊥BD于点F.
在Rt△ABF中,∠ABF=45°,AB=1,
∴BF=AF=,
∵在Rt△BDE中,DE=BE=3,
∴BD=3,
∴DF=BD﹣BF=3﹣=,
∴在Rt△AFD 中,AD===.
6.解:
(1)过点A作AD⊥BC于点D,
∵∠B=30°,
∴cos∠B==,
∴BD=AB,
∵△ABC是等腰三角形,
∴BC=2BD=AB,
故can30°==;
(2)过点A作AE⊥BC于点E,
∵canB=,则可设BC=8x,AB=5x,
∴AE==3x,
∵S△ABC=24,
∴BC×AE=12x2=24,
解得:x=,
故AB=AC=5,BC=8,
从而可得△ABC的周长为18.
7.解:(1)过点A作AD⊥BC于D.
∵AD⊥BC,
∴∠ADC=90°.
在Rt△ADC中,
∵∠C=45°,AC=2,
∴AD=DC=2,
在Rt△ABD中,
∵∠B=30°,AD=2,
∴AB=2AD=4.
(2)在Rt△ABD中,∵∠B=30°,AD=2,
∴AB=2AD=4.BD=AD=2,
∴S△ABC= BC AD=×2×(2+2)=2+2.
8.解:(1)∵DE垂直平分AB,
∴EA=EB,
∴∠EAB=∠B=25°.
∴∠CAE=40°.
(2)∵∠C=90°,
∴.
∵CE=2,
∴AE=3,
∴AC=,
∵EA=EB=3,
∴BC=5,
∴.
9.解:过点C作CH⊥AC,交AD于点H,
∵∠ACH=∠BAC=90°,
∴AB∥CH,
∴△DCH∽△DBA,
∴,
∴,
设CH=k,
∴AB=3k,
∴AC=4k,
∴tan∠CAD=,
∴tan∠CAD的值为.
10.解:(1)如图,过点D作DE⊥BC于点E,
在Rt△CED中,∵,
∴CE=DE=1,
在Rt△BDE中,;
(2)过点D作DF⊥AB于点F,
则∠BFD=∠BED=∠ABC=90°,
∴四边形BEDF是矩形,
∴DE=BF=1,
∵BD=3,
∴
∴AF=AB﹣BF=2,
∴
11.解:∵tanC===,
∴CD=4.
∴BD=12﹣4=8.
在Rt△ABD中,
AB=
=10.
∴cosB==.
12.解:如图,过点C作CD⊥AB于点D.
∵∠B=45°,CD⊥AB,
∴∠BCD=45°,
在Rt△BCD中,∠BDC=90°,BC=3,cos∠B=,
∴BD=cos∠B×BC=×3=3.
∵∠B=∠BCD=45°,
∴CD=BD=3.
在Rt△ACD中,∠ADC=90°,∠ACD=75°﹣45°=30°,
∴tan∠ACD=,
∴AD=tan∠ACD×CD=×3=,
∴AB=AD+BD=+3.
∵cos∠ACD=,
∴AC===2.
即:AB=+3,AC=2.
13.解:(1)如图,过点A作AD⊥BC于点D,
∵AB=AC=10,
∴BC=2BD,
在Rt△ABD中,∵sinB=,
∴AD=ABsinB=10×=8,
∴BD===6,
则BC=2BD=12;
(2)如图,过B作BH⊥AC于H,
∵S△ABC=AC BH=BC AD,
∴BH===,
∴AH===,
∴cos∠BAC===.
14.解:(1)设AC=3x,
∵∠C=90°,sin∠ABC=,
∴AB=5x,BC=4x,
∵tan∠DAC=,
∴CD=2x,
∵BD=4,BC=CD+BD,
∴4x=2x+4,
解得x=2,
∴AC=3x=6;
(2)作DE⊥AB于点E,
由(1)知,AB=5x=10,AC=6,BD=4,
∵,
∴,
解得DE=,
∵AC=6,CD=2x=4,∠C=90°,
∴AD==2,
∴AE===,
∴cot∠BAD===,
即cot∠BAD的值是.
15.解:(1)∵AB=AC,AD⊥BC,BC=18,
∴BD=DC=BC=9,
∴AB===3,
∴sinB===;
(2)∵AD⊥BC,EF⊥BC,
∴EF∥AD,
∴===,
∴EF=AD=×6=4,BF=BD=×9=6,
∴DF=BD﹣BF=9﹣6=3,
在Rt△DEF中,DE===5.
16.解:(1)∵在Rt△ABC中,∠ACB=90°,BC=12,cosB=,
∴,
∵D是斜边AB上的中点,
∴,
又∵点E是BC边上的中点,
∴点G是△ABC的重心,
∴;
(2)∵点E是BC边上的中点,
∴,
过点E作EF⊥AB,垂足为F,
∵在Rt△BEF中,cosB=,
BF=BE cosB=,
∴,
∵AF=AB﹣BF=18﹣4=14,
∴tan∠BAE=.
17.解:(1)过点A作AF⊥BC,垂足为F,
∵AB=AC=,BC=2.
∴BF=FC=BC=1,
在Rt△ACF中,cos∠ACB===;
(2)∵BD⊥AC,
∴∠BDC=90°,
在Rt△BDC中,
∴cos∠ACB=,
∴CD=BC cos∠ACB=2×=,
BD===,
又∵∠A=∠E,∠ADB=∠EDC=90°,
∴△ABD∽△ECD,
∴==,
∴EC=AB=,
答:EC的长为.
18.解:(1)过D作DF⊥AB于F,如图:
∵∠C=90°,AB=4,BC=2,
∴AC==2,sin∠BAC=,
∴∠BAC=30°,
∵点D是AC的中点,
∴AD=CD=,
∴BD==,
Rt△ADF中,DF=AD sin∠BAC=,
Rt△BDF中,sin∠ABE==;
(2)过A作AH⊥BE于H,过E作EG∥AC交BC延长线于G,如图:
∵∠ADH=∠BDC,∠BCD=∠AHD=90°,
∴△BCD∽△AHD,
∴,
∵BC=2,CD=AD=,BD=,
∴,解得AH=,HD=,
∵∠AEB=∠BAC=30°,
∴HE==,
∴BE=BD+DH+HE=,
∵EG∥AC,
∴∠BDC=∠BEG,
而∠CBD=∠GBE,
∴△CBD∽△GBE,
∴,即,
∴EG=.
方法二:过E作EG⊥BC于G,
∵∠E=∠BAC,∠ABE=∠DBA,
∴△ABD∽△ABE,
∴=,
即,
∴BE=,
∵DC⊥BC,EG⊥BG,
∴DC∥BG,
∴,即=,
∴EG=,
∴点E到直线BC的距离为.
19.解:(1)过C点作CH⊥AD于H,如图,
∵CD=CA,
∴AH=DH,
∵∠ABC+∠BCH=90°,∠ACH+∠BCH=90°,
∴∠ACH=∠ABC,
∴sin∠ACH=sin∠ABC=,
在Rt△ACH中,sin∠ACH==,
∴AD=2AH=2;
(2)在Rt△ABC中,sin∠ABC==,
∴AB=3AC=9,
∴BD=AB﹣AD=9﹣2=7,
∵∠E=90°,
而∠EDB=∠HDC,
∴∠HCD=∠EBD,
∴sin∠EBD==,
∴DE=BD=,
∴BE==,
在Rt△EBC中,tan∠EBC===.
20.解:(1)作AE⊥BC于E,如图,
∵AB=AC,
∴BE=CE=BC=×8=4,
在Rt△ABE中,cosB==;
(2)作DF⊥BC于F,如图,
在Rt△CDF中,tan∠DCF==,
设DF=3x,则CF=5x,
在Rt△ABE中,AE==3,
∴tanB==,
在Rt△BDF中,tanB==,
而DF=3x,
∴BF=4x,
∴BC=BF+CF=4x+5x=9x,
即9x=8,解得x=,
∴DF=3x=,
∴S△BCD=×DF×BC=××8=.
21.解:
(1)∵∠CAD:∠DAB=1:2
∴∠DAB=2∠CAD
在Rt△ABC中,∠CAD+∠DAB+∠DBA=90°
∵DE垂直平分AB交边BC、AB于点D、E
∴∠DAB=∠DBA
∴∠CAD+∠DAB+∠DBA=∠CAD+2∠CAD+2∠CAD=90°
解得,∠CAD=18°
(2)在Rt△ABC中,AC=1,tan∠B==,
∴BC=2
由勾股定理得,AB===
∵DE垂直平分AB交边BC、AB于点D、E
∴BE=AE=
∵∠DAE=∠DBE
∴在Rt△ADE中
tan∠B=tan∠DAE==
∴DE=
∴由勾股定理得
AD===
∴cos∠CAD===
∴sin∠CAD===
则∠CAD的正弦值为
22.解:(1)∵AB=AC,点D是边BC的中点,
∴AD⊥BC,BD=DC=BC=5,
在Rt△ABD中,cos∠ABC==,
∴AB=13;
(2)过点E作EH∥BC,交AD与点H,
∵EH∥BC,=,
∴==,
∵BD=CD,
∴=,
∵EH∥BC,
∴==.
23.解:(1)如图,在Rt△ABC中,
∵tanB==,
∴设AC=3x、BC=4x,
∵BD=2,
∴DC=BC﹣BD=4x﹣2,
∵∠ADC=45°,
∴AC=DC,即4x﹣2=3x,
解得:x=2,
则AC=6、BC=8,
∴AB==10;
(2)作DE⊥AB于点E,
由tanB==可设DE=3a,则BE=4a,
∵DE2+BE2=BD2,且BD=2,
∴(3a)2+(4a)2=22,解得:a=(负值舍去),
∴DE=3a=,
∵AD==6,
∴sin∠BAD==.
24.解:(1)∵BD⊥AC,
∴∠ADE=90°,
Rt△ADB中,AB=13,cos∠BAC=,
∴AD=5,
由勾股定理得:BD=12,
∵E是BD的中点,
∴ED=6,
∴∠EAD的余切==;
(2)过D作DG∥AF交BC于G,
∵AC=8,AD=5,
∴CD=3,
∵DG∥AF,
∴=,
设CG=3x,FG=5x,
∵EF∥DG,BE=ED,
∴BF=FG=5x,
∴==.
1.(1)计算:2tan60° tan30°﹣4cos245°+sin60°;
(2)如图,在△ABC中,tanC=,点D在边BC上,AB=AD,CD=2BD=4,求sinB的值.
2.如图,在△ABC中,AB=AC=10,.求sinA的值.
3.如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,sinB=,求:
(1)线段DC的长;
(2)sin∠EDC的值.
4.如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,点D在边BC上,且BD=3CD,DE⊥AB,垂足为点E,联结CE.
(1)求线段AE的长;
(2)求∠ACE的余切值.
5.已知:BD是四边形ABCD的对角线,AB⊥BC,∠C=60°,AB=1,BC=3+,CD=2
(1)求∠ABD的值;
(2)求AD的长.
6.通过学习锐角三角比,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can),如图(1)在△ABC中,AB=AC,底角B的邻对记作canB,这时canB=,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义,解下列问题:
(1)can30°= ;
(2)如图(2),已知在△ABC中,AB=AC,canB=,S△ABC=24,求△ABC的周长.
7.已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=2,
求(1)AB的长;
(2)S△ABC.
8.如图,在△ABC中,∠C=90°,AB的垂直平分线分别交边AB、BC于点D、E,连接AE.
(1)如果∠B=25°,求∠CAE的度数;
(2)如果CE=2,sin∠CAE=,求tanB的值.
9.如图,在Rt△ABC中,∠BAC=90°,延长斜边BC到点D,使CD=BC,联结AD,如果tanB=,求tan∠CAD的值.
10.如图,在四边形ABCD中,∠ABC=90°,∠C=45°,CD=,BD=3.
(1)求sin∠CBD的值;
(2)若AB=3,求AD的长.
11.如图,在△ABC中,AD⊥BC于点D,若AD=6.tanC=,BC=12,求cosB的值.
12.如图,在△ABC中,∠B=45°,∠C=75°,BC=3,求:AB、AC.
13.如图,在△ABC中,AB=AC=10,sinB=.
(1)求边BC的长度;
(2)求cosA的值.
14.如图,已知在Rt△ABC中,∠C=90°,sin∠ABC=,点D在边BC上,BD=4,联结AD,tan∠DAC=.
(1)求边AC的长;
(2)求cot∠BAD的值.
15.如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,BC=18,AD=6.
(1)求sinB的值;
(2)点E在AB上,且BE=2AE,过E作EF⊥BC,垂足为点F,求DE的长.
16.已知:如图,在Rt△ABC中,∠ACB=90°,BC=12,cosB=,D、E分别是AB、BC边上的中点,AE与CD相交于点G.
(1)求CG的长;
(2)求tan∠BAE的值.
17.如图,在△ABC中,AB=AC=,BC=2.过点B作BD⊥AC,垂足为点D.
(1)求cos∠ACB的值;
(2)点E是BD延长线上一点,联结CE,当∠E=∠A时,求线段CE的长.
18.如图,已知,在Rt△ABC中,∠C=90°,AB=4,BC=2,点D是AC的中点,联结BD并延长至点E,使∠E=∠BAC.
(1)求sin∠ABE的值;
(2)求点E到直线BC的距离.
19.如图,在Rt△ABC中,∠ACB=90°,AC=3,sin∠ABC=,D是边AB上一点,且CD=CA,BE⊥CD,垂足为点E.
(1)求AD的长;
(2)求∠EBC的正切值.
20.已知:如图,在△ABC中,AB=AC=5,BC=8,D是边AB上一点,且tan∠DCB=.
(1)试求cosB的值;
(2)试求△BCD的面积.
21.如图,在△ABC中,∠C=90°,AB的垂直平分线分别交边BC、AB于点D、E,联结AD.
(1)如果∠CAD:∠DAB=1:2,求∠CAD的度数;
(2)如果AC=1,tanB=,求∠CAD的正弦值.
22.如图,在△ABC中,AB=AC,BC=10,cos,点D是边BC的中点,点E在边AC上,且=,AD与BE相交于点F.求:
(1)边AB的长;
(2)的值.
23.如图,在Rt△ABC中,∠C=90°,点D在BC边上,∠ADC=45°,BD=2,tanB=
(1)求AC和AB的长;
(2)求sin∠BAD的值.
24.已知:如图,在△ABC中,AB=13,AC=8,cos∠BAC=,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
(1)求∠EAD的余切值;
(2)求的值.
参考答案
1.解:(1)2tan60° tan30°﹣4cos245°+sin60°
=2××﹣4×()2+
=2﹣4×+
=2﹣2+
=;
(2)作AE⊥BD于点E,
∵AB=AD,CD=2BD=4,
∴BE=DE=1,
∴CE=CD+DE=5,
∵tanC=,
∴,
∴AE=3,
∴AB===,
∴sinB=.
2.解:过点C作CD⊥AB,
在Rt△CDB中,
∵sinB==,
设CD=4x,BC=5x,
则BD=3x,
∴AD=10﹣3x,
在Rt△CDA中,由勾股定理得,
AC2=AD2+CD2,
即102=(10﹣3x)2+(4x)2,
整理得:25x2﹣60x=0,
解得:x=2.4或x=0(舍去),
∴CD=4x=9.6,
在Rt△CDA中,
sinA===.
3.解:(1)在△ABC中,∵AD是边BC上的高,
∴AD⊥BC.
∴sinB==.
∵AD=12,
∴AB===15.
在Rt△ABD中,∵BD===9,
∴CD=BC﹣BD=14﹣9=5.
(2)在Rt△ADC中,∵AD=12,DC=5,
∴AC=13.
∵E是AC的中点,
∴DE=EC,
∴∠EDC=∠C.
∴sin∠EDC=sin∠C==.
4.解:(1)∵BC=4,BD=3CD,
∴BD=3.
∵AB=BC,∠ACB=90°,
∴∠A=∠B=45°.
∵DE⊥AB,
∴在Rt△DEB中,.
∴
在Rt△ACB中,,
∴
(2)如图,过点E作EH⊥AC于点H.
∴在Rt△AHE中,,
AH=AE cos45°=,
∴,
∴EH=AH=,
∴在Rt△CHE中,cot∠ECH=,
即∠ACE的余切值是.
5.解:(1)过点D作DE⊥BC于点E,
∵在Rt△CDE 中,∠C=60°,CD=2,
∴CE=,DE=3,
∵BC=3+,
∴BE=BC﹣CE=3+﹣=3,
∴DE=BE=3,
∴在Rt△BDE 中,∠EDB=∠EBD=45°,
∵AB⊥BC,∠ABC=90°,
∴∠ABD=∠ABC﹣∠EBD=45°;
(2)过点A作AF⊥BD于点F.
在Rt△ABF中,∠ABF=45°,AB=1,
∴BF=AF=,
∵在Rt△BDE中,DE=BE=3,
∴BD=3,
∴DF=BD﹣BF=3﹣=,
∴在Rt△AFD 中,AD===.
6.解:
(1)过点A作AD⊥BC于点D,
∵∠B=30°,
∴cos∠B==,
∴BD=AB,
∵△ABC是等腰三角形,
∴BC=2BD=AB,
故can30°==;
(2)过点A作AE⊥BC于点E,
∵canB=,则可设BC=8x,AB=5x,
∴AE==3x,
∵S△ABC=24,
∴BC×AE=12x2=24,
解得:x=,
故AB=AC=5,BC=8,
从而可得△ABC的周长为18.
7.解:(1)过点A作AD⊥BC于D.
∵AD⊥BC,
∴∠ADC=90°.
在Rt△ADC中,
∵∠C=45°,AC=2,
∴AD=DC=2,
在Rt△ABD中,
∵∠B=30°,AD=2,
∴AB=2AD=4.
(2)在Rt△ABD中,∵∠B=30°,AD=2,
∴AB=2AD=4.BD=AD=2,
∴S△ABC= BC AD=×2×(2+2)=2+2.
8.解:(1)∵DE垂直平分AB,
∴EA=EB,
∴∠EAB=∠B=25°.
∴∠CAE=40°.
(2)∵∠C=90°,
∴.
∵CE=2,
∴AE=3,
∴AC=,
∵EA=EB=3,
∴BC=5,
∴.
9.解:过点C作CH⊥AC,交AD于点H,
∵∠ACH=∠BAC=90°,
∴AB∥CH,
∴△DCH∽△DBA,
∴,
∴,
设CH=k,
∴AB=3k,
∴AC=4k,
∴tan∠CAD=,
∴tan∠CAD的值为.
10.解:(1)如图,过点D作DE⊥BC于点E,
在Rt△CED中,∵,
∴CE=DE=1,
在Rt△BDE中,;
(2)过点D作DF⊥AB于点F,
则∠BFD=∠BED=∠ABC=90°,
∴四边形BEDF是矩形,
∴DE=BF=1,
∵BD=3,
∴
∴AF=AB﹣BF=2,
∴
11.解:∵tanC===,
∴CD=4.
∴BD=12﹣4=8.
在Rt△ABD中,
AB=
=10.
∴cosB==.
12.解:如图,过点C作CD⊥AB于点D.
∵∠B=45°,CD⊥AB,
∴∠BCD=45°,
在Rt△BCD中,∠BDC=90°,BC=3,cos∠B=,
∴BD=cos∠B×BC=×3=3.
∵∠B=∠BCD=45°,
∴CD=BD=3.
在Rt△ACD中,∠ADC=90°,∠ACD=75°﹣45°=30°,
∴tan∠ACD=,
∴AD=tan∠ACD×CD=×3=,
∴AB=AD+BD=+3.
∵cos∠ACD=,
∴AC===2.
即:AB=+3,AC=2.
13.解:(1)如图,过点A作AD⊥BC于点D,
∵AB=AC=10,
∴BC=2BD,
在Rt△ABD中,∵sinB=,
∴AD=ABsinB=10×=8,
∴BD===6,
则BC=2BD=12;
(2)如图,过B作BH⊥AC于H,
∵S△ABC=AC BH=BC AD,
∴BH===,
∴AH===,
∴cos∠BAC===.
14.解:(1)设AC=3x,
∵∠C=90°,sin∠ABC=,
∴AB=5x,BC=4x,
∵tan∠DAC=,
∴CD=2x,
∵BD=4,BC=CD+BD,
∴4x=2x+4,
解得x=2,
∴AC=3x=6;
(2)作DE⊥AB于点E,
由(1)知,AB=5x=10,AC=6,BD=4,
∵,
∴,
解得DE=,
∵AC=6,CD=2x=4,∠C=90°,
∴AD==2,
∴AE===,
∴cot∠BAD===,
即cot∠BAD的值是.
15.解:(1)∵AB=AC,AD⊥BC,BC=18,
∴BD=DC=BC=9,
∴AB===3,
∴sinB===;
(2)∵AD⊥BC,EF⊥BC,
∴EF∥AD,
∴===,
∴EF=AD=×6=4,BF=BD=×9=6,
∴DF=BD﹣BF=9﹣6=3,
在Rt△DEF中,DE===5.
16.解:(1)∵在Rt△ABC中,∠ACB=90°,BC=12,cosB=,
∴,
∵D是斜边AB上的中点,
∴,
又∵点E是BC边上的中点,
∴点G是△ABC的重心,
∴;
(2)∵点E是BC边上的中点,
∴,
过点E作EF⊥AB,垂足为F,
∵在Rt△BEF中,cosB=,
BF=BE cosB=,
∴,
∵AF=AB﹣BF=18﹣4=14,
∴tan∠BAE=.
17.解:(1)过点A作AF⊥BC,垂足为F,
∵AB=AC=,BC=2.
∴BF=FC=BC=1,
在Rt△ACF中,cos∠ACB===;
(2)∵BD⊥AC,
∴∠BDC=90°,
在Rt△BDC中,
∴cos∠ACB=,
∴CD=BC cos∠ACB=2×=,
BD===,
又∵∠A=∠E,∠ADB=∠EDC=90°,
∴△ABD∽△ECD,
∴==,
∴EC=AB=,
答:EC的长为.
18.解:(1)过D作DF⊥AB于F,如图:
∵∠C=90°,AB=4,BC=2,
∴AC==2,sin∠BAC=,
∴∠BAC=30°,
∵点D是AC的中点,
∴AD=CD=,
∴BD==,
Rt△ADF中,DF=AD sin∠BAC=,
Rt△BDF中,sin∠ABE==;
(2)过A作AH⊥BE于H,过E作EG∥AC交BC延长线于G,如图:
∵∠ADH=∠BDC,∠BCD=∠AHD=90°,
∴△BCD∽△AHD,
∴,
∵BC=2,CD=AD=,BD=,
∴,解得AH=,HD=,
∵∠AEB=∠BAC=30°,
∴HE==,
∴BE=BD+DH+HE=,
∵EG∥AC,
∴∠BDC=∠BEG,
而∠CBD=∠GBE,
∴△CBD∽△GBE,
∴,即,
∴EG=.
方法二:过E作EG⊥BC于G,
∵∠E=∠BAC,∠ABE=∠DBA,
∴△ABD∽△ABE,
∴=,
即,
∴BE=,
∵DC⊥BC,EG⊥BG,
∴DC∥BG,
∴,即=,
∴EG=,
∴点E到直线BC的距离为.
19.解:(1)过C点作CH⊥AD于H,如图,
∵CD=CA,
∴AH=DH,
∵∠ABC+∠BCH=90°,∠ACH+∠BCH=90°,
∴∠ACH=∠ABC,
∴sin∠ACH=sin∠ABC=,
在Rt△ACH中,sin∠ACH==,
∴AD=2AH=2;
(2)在Rt△ABC中,sin∠ABC==,
∴AB=3AC=9,
∴BD=AB﹣AD=9﹣2=7,
∵∠E=90°,
而∠EDB=∠HDC,
∴∠HCD=∠EBD,
∴sin∠EBD==,
∴DE=BD=,
∴BE==,
在Rt△EBC中,tan∠EBC===.
20.解:(1)作AE⊥BC于E,如图,
∵AB=AC,
∴BE=CE=BC=×8=4,
在Rt△ABE中,cosB==;
(2)作DF⊥BC于F,如图,
在Rt△CDF中,tan∠DCF==,
设DF=3x,则CF=5x,
在Rt△ABE中,AE==3,
∴tanB==,
在Rt△BDF中,tanB==,
而DF=3x,
∴BF=4x,
∴BC=BF+CF=4x+5x=9x,
即9x=8,解得x=,
∴DF=3x=,
∴S△BCD=×DF×BC=××8=.
21.解:
(1)∵∠CAD:∠DAB=1:2
∴∠DAB=2∠CAD
在Rt△ABC中,∠CAD+∠DAB+∠DBA=90°
∵DE垂直平分AB交边BC、AB于点D、E
∴∠DAB=∠DBA
∴∠CAD+∠DAB+∠DBA=∠CAD+2∠CAD+2∠CAD=90°
解得,∠CAD=18°
(2)在Rt△ABC中,AC=1,tan∠B==,
∴BC=2
由勾股定理得,AB===
∵DE垂直平分AB交边BC、AB于点D、E
∴BE=AE=
∵∠DAE=∠DBE
∴在Rt△ADE中
tan∠B=tan∠DAE==
∴DE=
∴由勾股定理得
AD===
∴cos∠CAD===
∴sin∠CAD===
则∠CAD的正弦值为
22.解:(1)∵AB=AC,点D是边BC的中点,
∴AD⊥BC,BD=DC=BC=5,
在Rt△ABD中,cos∠ABC==,
∴AB=13;
(2)过点E作EH∥BC,交AD与点H,
∵EH∥BC,=,
∴==,
∵BD=CD,
∴=,
∵EH∥BC,
∴==.
23.解:(1)如图,在Rt△ABC中,
∵tanB==,
∴设AC=3x、BC=4x,
∵BD=2,
∴DC=BC﹣BD=4x﹣2,
∵∠ADC=45°,
∴AC=DC,即4x﹣2=3x,
解得:x=2,
则AC=6、BC=8,
∴AB==10;
(2)作DE⊥AB于点E,
由tanB==可设DE=3a,则BE=4a,
∵DE2+BE2=BD2,且BD=2,
∴(3a)2+(4a)2=22,解得:a=(负值舍去),
∴DE=3a=,
∵AD==6,
∴sin∠BAD==.
24.解:(1)∵BD⊥AC,
∴∠ADE=90°,
Rt△ADB中,AB=13,cos∠BAC=,
∴AD=5,
由勾股定理得:BD=12,
∵E是BD的中点,
∴ED=6,
∴∠EAD的余切==;
(2)过D作DG∥AF交BC于G,
∵AC=8,AD=5,
∴CD=3,
∵DG∥AF,
∴=,
设CG=3x,FG=5x,
∵EF∥DG,BE=ED,
∴BF=FG=5x,
∴==.
