2021-2022学年北师大版九年级数学下册1.6 利用三角函数测高 同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册1.6 利用三角函数测高 同步练习题(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 533.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-21 23:10:41 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学下册《1.6利用三角函数测高》同步练习题(附答案)
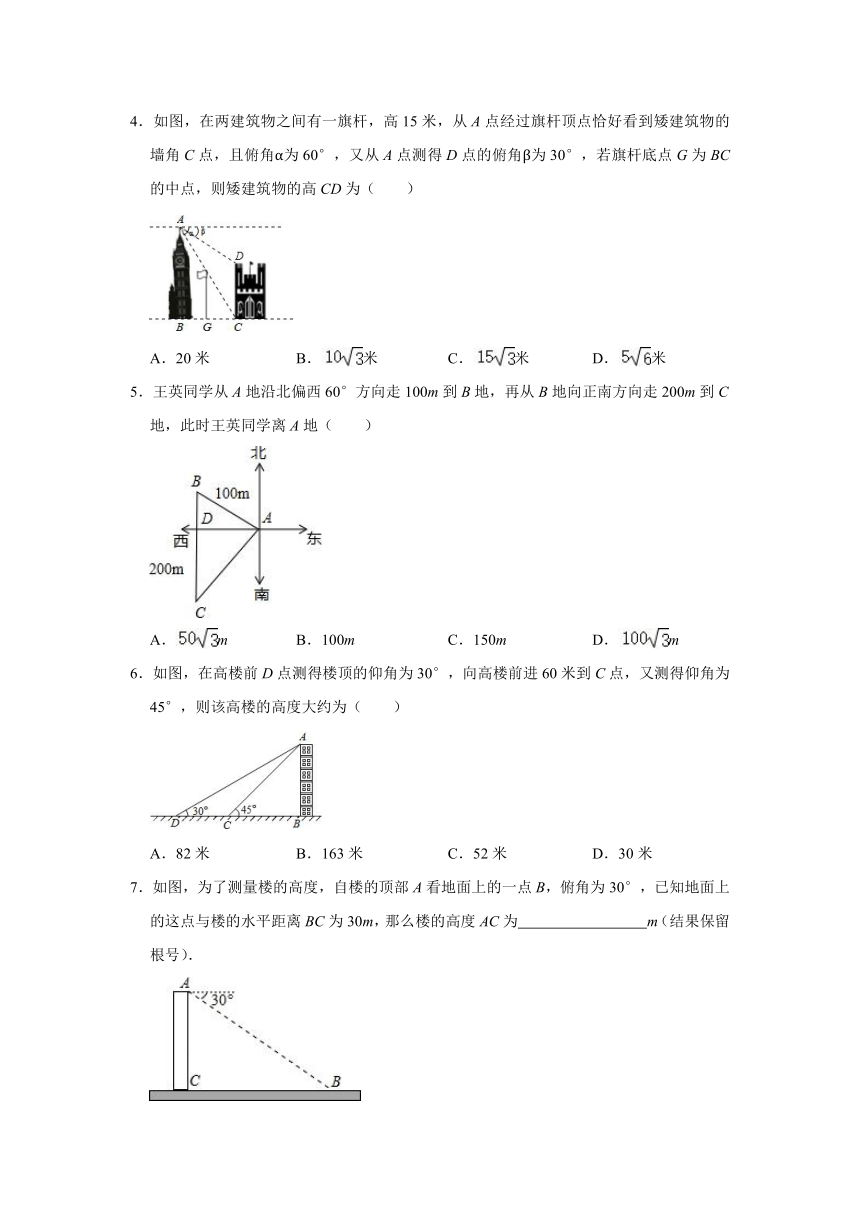
1.如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
A.50 B.51 C.50+1 D.101
2.如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上).为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30°,则B、C两地之间的距离为( )
A.100m B.50m C.50m D.m
3.如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )
A.40海里 B.40海里 C.80海里 D.40海里
4.如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( )
A.20米 B.米 C.米 D.米
5.王英同学从A地沿北偏西60°方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地( )
A.m B.100m C.150m D.m
6.如图,在高楼前D点测得楼顶的仰角为30°,向高楼前进60米到C点,又测得仰角为45°,则该高楼的高度大约为( )
A.82米 B.163米 C.52米 D.30米
7.如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为 m(结果保留根号).
8.如图,在小山的东侧A点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为 米.
9.如图,两建筑物的水平距离BC为18m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°.则建筑物CD的高度为 m(结果不作近似计算).
10.小兰想测量南塔的高度.她在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处,测得仰角为60°,那么塔高约为 m.(小兰身高忽略不计,取)
11.某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼三楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知每层楼的高度为3米,则旗杆AB的高度为 米.
12.如图,建筑物AB后有一座假山,其坡度为i=1:,山坡上E点处有一凉亭,测得假山坡脚C与建筑物水平距离BC=25米,与凉亭距离CE=20米,某人从建筑物顶端测得E点的俯角为45°,求建筑物AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
13.如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船c的求救信号.已知A、B两船相距100(+3)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
(1)分别求出A与C,A与D之间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距观测点D处200海里范围内有暗礁.若巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险?(参考数据:≈1.41,≈1.73)
14.某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
15.军方派出搜救船在失事海域搜寻飞机残骸和黑匣子(如图).在海面A处搜救船测得俯角为30°正前方的海底有黑匣子信号发出,继续直线航行2千米后再次在B处测得俯角为45°正前方的海底有黑匣子信号发出,求海底C处距离海面的深度?(参考数据:)
16.如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上).
(1)用含α、β和m的式子表示h;
(2)当α=45°,β=60°,m=50米时,求h的值.
(精确到0.1m,≈1.41,≈1.73)
17.国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图1,在一次巡航过程中,巡航飞机飞行高度为2021米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1200米到达B点后测得F点俯角为45°,如图2.请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数值:=1.732,=1.414)
18.天塔是天津市的标志性建筑之一,某校数学兴趣小组要测量天塔的高度,如图,他们在点A处测得天塔最高点C的仰角为45°,再往天塔方向前进至点B处测得最高点C的仰角为54°,AB=112m,根据这个兴趣小组测得的数据,计算天塔的高度CD(tan36°≈0.73,结果保留整数).
19.如图,在与河对岸平行的南岸边有A、B、D三点,A、B、D三点在同一直线上,在A点处测得河对岸C点在北偏东60°方向;从A点沿河边前进200米到达B点,这时测得C点在北偏东30°方向,求河宽CD.
20.如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取=1.732,结果精确到1m)
21.今年五、六月份,我省各地、市普遭暴雨袭击,水位猛涨.某市抗洪抢险救援队伍在B处接到报告:有受灾群众被困于一座遭水淹的楼顶A处,情况危急!救援队伍在B处测得A在B的北偏东60°的方向上(如图所示),队伍决定分成两组:第一组马上下水游向A处救人,同时第二组从陆地往正东方向奔跑120米到达C处,再从C处下水游向A处救人,已知A在C的北偏东30°的方向上,且救援人员在水中游进的速度均为1米/秒.在陆地上奔跑的速度为4米/秒,试问哪组救援队先到A处?请说明理由.
(参考数据=1.732)
22.海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
23.某中学初三(2)班数学活动小组利用周日开展课外实践活动,他们要在湖面上测量建在地面上某塔AB的高度.如图,在湖面上点C测得塔顶A的仰角为45°,沿直线CD向塔AB方向前进18米到达点D,测得塔顶A的仰角为60度.已知湖面低于地平面1米,请你帮他们计算出塔AB的高度.(结果保留根号)
24.如图,在测量塔高AB时,选择与塔底在同一水平面的同一直线上的C、D两点,用测角仪器测得塔顶A的仰角分别是30°和60°,已知测角仪器高CE=1.5米,CD=30米,求塔高AB.(保留根号)
25.如图,要测量A点到河岸BC的距离,在B点测得A点在B点的北偏东30°方向上,在C点测得A点在C点的北偏西45°方向上,又测得BC=150m.求A点到河岸BC的距离.(结果保留整数)(参考数据:≈1.41,≈1.73)
参考答案
1.解:设AG=x米,
在Rt△AEG中,
∵tan∠AEG=,
∴EG==x(m),
在Rt△ACG中,
∵tan∠ACG=,
∴CG==x(m),
∴x﹣x=100,
解得:x=50.
则AB=(50+1)米.
故选:C.
2.解:根据题意得:∠ABC=30°,AC⊥BC,AC=100m,
在Rt△ABC中,BC===100(m).
故选:A.
3.解:过点P作PC⊥AB于点C,
由题意可得出:∠A=30°,∠B=45°,AP=80海里,
故CP=AP=40(海里),
则PB==40(海里).
故选:A.
4.解:∵点G是BC中点,EG∥AB,
∴EG是△ABC的中位线,
∴AB=2EG=30米,
在Rt△ABC中,∠CAB=30°,
则BC=ABtan∠BAC=30×=10米.
如图,过点D作DF⊥AF于点F.
在Rt△AFD中,AF=BC=10米,
则FD=AF tanβ=10×=10米,
综上可得:CD=AB﹣FD=30﹣10=20米.
故选:A.
5.解:AD=AB sin60°=50;
BD=AB cos60°=50,∴CD=150.
∴AC==100.
故选:D.
6.解:设楼高AB为x.
在Rt△ADB中有:DB==x,
在Rt△ACB中有:BC==x.
而CD=BD﹣BC=(﹣1)x=60,
解得x≈82.故选:A.
7.解:∵自楼的顶部A看地面上的一点B,俯角为30°,
∴∠ABC=30°,
∴AC=AB tan30°=30×=10(米).
∴楼的高度AC为10米.
故答案为:10.
8.解:如图,过点A作AD⊥BC,垂足为D,
在Rt△ACD中,∠ACD=75°﹣30°=45°,
AC=30×25=750(米),
∴AD=AC sin45°=375(米).
在Rt△ABD中,
∵∠B=30°,
∴AB=2AD=750(米).
故答案为:750.
9.解:过点D作DE⊥AB于点E,
则四边形BCDE是矩形,
根据题意得:∠ACB=β=60°,∠ADE=α=30°,BC=18m,
∴DE=BC=18m,CD=BE,
在Rt△ABC中,AB=BC tan∠ACB=18×tan60°=18(m),
在Rt△ADE中,AE=DE tan∠ADE=18×tan30°=6(m),
∴DC=BE=AB﹣AE=18﹣6=12(m).
故答案为:12.
10.解:∵∠DAB=30°,∠DBC=60°,
∴BD=AB=50m.
∴DC=BD sin60°=50×=43.3.
故答案为:43.3.
11.解:过点D作DE⊥AB,垂足为E,由题意可知,四边形ACDE为矩形,
则AE=CD=6米,AC=DE.
设BE=x米.
在Rt△BDE中,∵∠BED=90°,∠BDE=30°,
∴DE=BE=x米,
∴AC=DE=x米.
在Rt△ABC中,∵∠BAC=90°,∠ACB=60°,
∴AB=AC=×x=3x米,
∵AB﹣BE=AE,
∴3x﹣x=6,
∴x=3,
AB=3×3=9(米).
即旗杆AB的高度为9米.故答案为9.
12.解:过点E作EF⊥BC于点F,过点E作EN⊥AB于点N,
∵建筑物AB后有一座假山,其坡度为i=1:,
∴设EF=x,则FC=x,
∵CE=20米,
∴x2+(x)2=400,
解得:x=10,
则FC=10m,
∵BC=25m,∴BF=NE=(25+10)m,
∴AB=AN+BN=NE+EF=10+25+10=(35+10)m,
答:建筑物AB的高为(35+10)m.
13.解:(1)作CE⊥AB于点E,则∠ABC=45°,∠BAC=60°,设AE=x海里,
∵在Rt△AEC中,CE=AE tan60°=x,
在Rt△BCE中,BE=CE=x,
∴AE+BE=x+x=100(3+),解得x=100,
∴AC=2x=200.
在△ACD中,
∵∠DAC=60°,∠ADC=75°,
∴∠ACD=45°.
过点D作DF⊥AC于点F,设AF=y,则DF=CF=y,
∴AC=y+y=200,解得y=100(3﹣),
∴AD=2y=200(3﹣).
答:A与C之间的距离AC为200海里,A与D之间的距离AD为200(3﹣)海里;
(2)∵由(1)可知,DF=AF=×100(3﹣)≈219.
∵219>200,
∴巡逻船A沿直线AC去营救船C,在去营救的途中无触暗礁危险.
14.解:在Rt△CDA中,∠ACD=30°,CD=3000米,
∴AD=CDtan∠ACD=1000米,
在Rt△CDB中,∠BCD=60°,
∴BD=CDtan∠BCD=3000米,
∴AB=BD﹣AD=2000米.
答:此时渔政船和渔船相距2000米.
15.解:过C作CD垂直AB于D点,
设CD为x,在Rt△ACD与Rt△BCD中,∠CAD=30°,∠CBD=45°,AC=CD=2x,AD=AB+CD=2+x,
∴在Rt△ACD中有:(2+x)2+x2=(2x)2,
∴(舍去).
答:海底C处距海面2.732千米.
16.解:
(1)在Rt△ABC中,有BC=AB÷tanα=;
同理:在Rt△ABD中,有BD=AB÷tanβ=;
且CD=BC﹣BD=m;即﹣=m;
故h=,
(2)将α=45°,β=60°,m=50米,代入(1)中关系式可得
h=,
=,
=75米+25米,
≈118.3米.
17.解:设CF=x米,
在Rt△ACF和Rt△BCF中,
∵∠BAF=30°,∠CBF=45°,
∴BC=CF=x米,
=tan30°,
即AC=x米,
∵AC﹣BC=1200米,
∴x﹣x=1200,
解得:x=600(+1),
则DF=h﹣x=2021﹣600(+1)≈382(米).
答:钓鱼岛的最高海拔高度约382米.
18.解:根据题意得:∠CAD=45°,∠CBD=54°,AB=112m,
∵在Rt△ACD中,∠ACD=∠CAD=45°,
∴AD=CD,
∵AD=AB+BD,
∴BD=AD﹣AB=CD﹣112(m),
∵在Rt△BCD中,tan∠BCD=,∠BCD=90°﹣∠CBD=36°,
∴tan36°=,
∴BD=CD tan36°,
∴CD tan36°=CD﹣112,
∴CD=≈≈415(m).
答:天塔的高度CD约为:415m.
19.解:根据题意得:∠CAB=90°﹣60°=30°,∠CBD=90°﹣30°=60°,AB=200米,CD⊥AB,
则∠ACB=∠CBD﹣∠CAB=60°﹣30°=30°,
则BC=AB=200米,
在Rt△CBD中,CD=BC sin60°=200×=100(米).
答:河宽CD为100米.
20.解:设CE=xm,则由题意可知BE=xm,AE=(x+100)m.
在Rt△AEC中,tan∠CAE=,
即tan30°=,
∴,
3x=(x+100),
解得x=50+50=136.6,
∴CD=CE+ED=136.6+1.5=138.1≈138(m).
答:该建筑物的高度约为138m.
21.解:过A作AD⊥BC,交BC的延长线于点D,
∵A在B北偏东60°方向上,
∴∠ABD=30°,
又∵A在C北偏东30°方向上,
∴∠ACD=60°
又∵∠ABC=30°,所以∠BAC=30°,
∴∠ABD=∠BAC,所以AC=BC
∵BC=120,所以AC=120
在Rt△ACD中,∠ACD=60°,AC=120,
∴CD=60,AD=
在Rt△ABD中,∵∠ABD=30°,
∴AB=
第一组时间:
第二组时间:
因为207.84>150所以第二组先到达A处.
答:第二组先到.
22.解:有触礁危险.
理由:过点P作PD⊥AC于D.
设PD为x,在Rt△PBD中,
∠PBD=90°﹣45°=45度.
∴BD=PD=x.
在Rt△PAD中,
∵∠PAD=90°﹣60°=30°
∴AD=x
∵AD=AB+BD∴x=12+x
∴x=
∵6(+1)<18
∴渔船不改变航线继续向东航行,有触礁危险.
23.解:如图,延长CD,交AB的延长线于点E,
则∠AEC=90°,∠ACE=45°,∠ADE=60°,CD=18,
设线段AE的长为x米,
在Rt△ACE中,
∵∠ACE=45°,
∴CE=x,
在Rt△ADE中,
∵tan∠ADE=tan60°=,
∴DE=x,
∵CD=18,且CE﹣DE=CD,
∴x﹣x=18,
解得:x=27+9,
∵BE=1米,
∴AB=AE﹣BE=(26+9)(米).
答:塔AB的高度是(26+9)米.
24.解:设AF=x;
在Rt△AGF中,有GF==x,
同理在Rt△AEF中,有EF==x.
结合图形可得:GE=CD=EF﹣GF=30
即x﹣x=30,
解可得:x=15;故AB=15+
答:塔高AB为15+米.
25.解:过点A作AD⊥BC于点D,设AD=xm.
在Rt△ABD中,∵∠ADB=90°,∠BAD=30°,
∴BD=AD tan30°=x.
在Rt△ACD中,∵∠ADC=90°,∠CAD=45°,
∴CD=AD=x.
∵BD+CD=BC,
∴x+x=150,
∴x=75(3﹣)≈95.
即A点到河岸BC的距离约为95m.
1.如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
A.50 B.51 C.50+1 D.101
2.如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上).为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30°,则B、C两地之间的距离为( )
A.100m B.50m C.50m D.m
3.如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )
A.40海里 B.40海里 C.80海里 D.40海里
4.如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( )
A.20米 B.米 C.米 D.米
5.王英同学从A地沿北偏西60°方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地( )
A.m B.100m C.150m D.m
6.如图,在高楼前D点测得楼顶的仰角为30°,向高楼前进60米到C点,又测得仰角为45°,则该高楼的高度大约为( )
A.82米 B.163米 C.52米 D.30米
7.如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为 m(结果保留根号).
8.如图,在小山的东侧A点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为 米.
9.如图,两建筑物的水平距离BC为18m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°.则建筑物CD的高度为 m(结果不作近似计算).
10.小兰想测量南塔的高度.她在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处,测得仰角为60°,那么塔高约为 m.(小兰身高忽略不计,取)
11.某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼三楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知每层楼的高度为3米,则旗杆AB的高度为 米.
12.如图,建筑物AB后有一座假山,其坡度为i=1:,山坡上E点处有一凉亭,测得假山坡脚C与建筑物水平距离BC=25米,与凉亭距离CE=20米,某人从建筑物顶端测得E点的俯角为45°,求建筑物AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
13.如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船c的求救信号.已知A、B两船相距100(+3)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
(1)分别求出A与C,A与D之间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距观测点D处200海里范围内有暗礁.若巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险?(参考数据:≈1.41,≈1.73)
14.某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
15.军方派出搜救船在失事海域搜寻飞机残骸和黑匣子(如图).在海面A处搜救船测得俯角为30°正前方的海底有黑匣子信号发出,继续直线航行2千米后再次在B处测得俯角为45°正前方的海底有黑匣子信号发出,求海底C处距离海面的深度?(参考数据:)
16.如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上).
(1)用含α、β和m的式子表示h;
(2)当α=45°,β=60°,m=50米时,求h的值.
(精确到0.1m,≈1.41,≈1.73)
17.国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图1,在一次巡航过程中,巡航飞机飞行高度为2021米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1200米到达B点后测得F点俯角为45°,如图2.请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数值:=1.732,=1.414)
18.天塔是天津市的标志性建筑之一,某校数学兴趣小组要测量天塔的高度,如图,他们在点A处测得天塔最高点C的仰角为45°,再往天塔方向前进至点B处测得最高点C的仰角为54°,AB=112m,根据这个兴趣小组测得的数据,计算天塔的高度CD(tan36°≈0.73,结果保留整数).
19.如图,在与河对岸平行的南岸边有A、B、D三点,A、B、D三点在同一直线上,在A点处测得河对岸C点在北偏东60°方向;从A点沿河边前进200米到达B点,这时测得C点在北偏东30°方向,求河宽CD.
20.如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取=1.732,结果精确到1m)
21.今年五、六月份,我省各地、市普遭暴雨袭击,水位猛涨.某市抗洪抢险救援队伍在B处接到报告:有受灾群众被困于一座遭水淹的楼顶A处,情况危急!救援队伍在B处测得A在B的北偏东60°的方向上(如图所示),队伍决定分成两组:第一组马上下水游向A处救人,同时第二组从陆地往正东方向奔跑120米到达C处,再从C处下水游向A处救人,已知A在C的北偏东30°的方向上,且救援人员在水中游进的速度均为1米/秒.在陆地上奔跑的速度为4米/秒,试问哪组救援队先到A处?请说明理由.
(参考数据=1.732)
22.海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
23.某中学初三(2)班数学活动小组利用周日开展课外实践活动,他们要在湖面上测量建在地面上某塔AB的高度.如图,在湖面上点C测得塔顶A的仰角为45°,沿直线CD向塔AB方向前进18米到达点D,测得塔顶A的仰角为60度.已知湖面低于地平面1米,请你帮他们计算出塔AB的高度.(结果保留根号)
24.如图,在测量塔高AB时,选择与塔底在同一水平面的同一直线上的C、D两点,用测角仪器测得塔顶A的仰角分别是30°和60°,已知测角仪器高CE=1.5米,CD=30米,求塔高AB.(保留根号)
25.如图,要测量A点到河岸BC的距离,在B点测得A点在B点的北偏东30°方向上,在C点测得A点在C点的北偏西45°方向上,又测得BC=150m.求A点到河岸BC的距离.(结果保留整数)(参考数据:≈1.41,≈1.73)
参考答案
1.解:设AG=x米,
在Rt△AEG中,
∵tan∠AEG=,
∴EG==x(m),
在Rt△ACG中,
∵tan∠ACG=,
∴CG==x(m),
∴x﹣x=100,
解得:x=50.
则AB=(50+1)米.
故选:C.
2.解:根据题意得:∠ABC=30°,AC⊥BC,AC=100m,
在Rt△ABC中,BC===100(m).
故选:A.
3.解:过点P作PC⊥AB于点C,
由题意可得出:∠A=30°,∠B=45°,AP=80海里,
故CP=AP=40(海里),
则PB==40(海里).
故选:A.
4.解:∵点G是BC中点,EG∥AB,
∴EG是△ABC的中位线,
∴AB=2EG=30米,
在Rt△ABC中,∠CAB=30°,
则BC=ABtan∠BAC=30×=10米.
如图,过点D作DF⊥AF于点F.
在Rt△AFD中,AF=BC=10米,
则FD=AF tanβ=10×=10米,
综上可得:CD=AB﹣FD=30﹣10=20米.
故选:A.
5.解:AD=AB sin60°=50;
BD=AB cos60°=50,∴CD=150.
∴AC==100.
故选:D.
6.解:设楼高AB为x.
在Rt△ADB中有:DB==x,
在Rt△ACB中有:BC==x.
而CD=BD﹣BC=(﹣1)x=60,
解得x≈82.故选:A.
7.解:∵自楼的顶部A看地面上的一点B,俯角为30°,
∴∠ABC=30°,
∴AC=AB tan30°=30×=10(米).
∴楼的高度AC为10米.
故答案为:10.
8.解:如图,过点A作AD⊥BC,垂足为D,
在Rt△ACD中,∠ACD=75°﹣30°=45°,
AC=30×25=750(米),
∴AD=AC sin45°=375(米).
在Rt△ABD中,
∵∠B=30°,
∴AB=2AD=750(米).
故答案为:750.
9.解:过点D作DE⊥AB于点E,
则四边形BCDE是矩形,
根据题意得:∠ACB=β=60°,∠ADE=α=30°,BC=18m,
∴DE=BC=18m,CD=BE,
在Rt△ABC中,AB=BC tan∠ACB=18×tan60°=18(m),
在Rt△ADE中,AE=DE tan∠ADE=18×tan30°=6(m),
∴DC=BE=AB﹣AE=18﹣6=12(m).
故答案为:12.
10.解:∵∠DAB=30°,∠DBC=60°,
∴BD=AB=50m.
∴DC=BD sin60°=50×=43.3.
故答案为:43.3.
11.解:过点D作DE⊥AB,垂足为E,由题意可知,四边形ACDE为矩形,
则AE=CD=6米,AC=DE.
设BE=x米.
在Rt△BDE中,∵∠BED=90°,∠BDE=30°,
∴DE=BE=x米,
∴AC=DE=x米.
在Rt△ABC中,∵∠BAC=90°,∠ACB=60°,
∴AB=AC=×x=3x米,
∵AB﹣BE=AE,
∴3x﹣x=6,
∴x=3,
AB=3×3=9(米).
即旗杆AB的高度为9米.故答案为9.
12.解:过点E作EF⊥BC于点F,过点E作EN⊥AB于点N,
∵建筑物AB后有一座假山,其坡度为i=1:,
∴设EF=x,则FC=x,
∵CE=20米,
∴x2+(x)2=400,
解得:x=10,
则FC=10m,
∵BC=25m,∴BF=NE=(25+10)m,
∴AB=AN+BN=NE+EF=10+25+10=(35+10)m,
答:建筑物AB的高为(35+10)m.
13.解:(1)作CE⊥AB于点E,则∠ABC=45°,∠BAC=60°,设AE=x海里,
∵在Rt△AEC中,CE=AE tan60°=x,
在Rt△BCE中,BE=CE=x,
∴AE+BE=x+x=100(3+),解得x=100,
∴AC=2x=200.
在△ACD中,
∵∠DAC=60°,∠ADC=75°,
∴∠ACD=45°.
过点D作DF⊥AC于点F,设AF=y,则DF=CF=y,
∴AC=y+y=200,解得y=100(3﹣),
∴AD=2y=200(3﹣).
答:A与C之间的距离AC为200海里,A与D之间的距离AD为200(3﹣)海里;
(2)∵由(1)可知,DF=AF=×100(3﹣)≈219.
∵219>200,
∴巡逻船A沿直线AC去营救船C,在去营救的途中无触暗礁危险.
14.解:在Rt△CDA中,∠ACD=30°,CD=3000米,
∴AD=CDtan∠ACD=1000米,
在Rt△CDB中,∠BCD=60°,
∴BD=CDtan∠BCD=3000米,
∴AB=BD﹣AD=2000米.
答:此时渔政船和渔船相距2000米.
15.解:过C作CD垂直AB于D点,
设CD为x,在Rt△ACD与Rt△BCD中,∠CAD=30°,∠CBD=45°,AC=CD=2x,AD=AB+CD=2+x,
∴在Rt△ACD中有:(2+x)2+x2=(2x)2,
∴(舍去).
答:海底C处距海面2.732千米.
16.解:
(1)在Rt△ABC中,有BC=AB÷tanα=;
同理:在Rt△ABD中,有BD=AB÷tanβ=;
且CD=BC﹣BD=m;即﹣=m;
故h=,
(2)将α=45°,β=60°,m=50米,代入(1)中关系式可得
h=,
=,
=75米+25米,
≈118.3米.
17.解:设CF=x米,
在Rt△ACF和Rt△BCF中,
∵∠BAF=30°,∠CBF=45°,
∴BC=CF=x米,
=tan30°,
即AC=x米,
∵AC﹣BC=1200米,
∴x﹣x=1200,
解得:x=600(+1),
则DF=h﹣x=2021﹣600(+1)≈382(米).
答:钓鱼岛的最高海拔高度约382米.
18.解:根据题意得:∠CAD=45°,∠CBD=54°,AB=112m,
∵在Rt△ACD中,∠ACD=∠CAD=45°,
∴AD=CD,
∵AD=AB+BD,
∴BD=AD﹣AB=CD﹣112(m),
∵在Rt△BCD中,tan∠BCD=,∠BCD=90°﹣∠CBD=36°,
∴tan36°=,
∴BD=CD tan36°,
∴CD tan36°=CD﹣112,
∴CD=≈≈415(m).
答:天塔的高度CD约为:415m.
19.解:根据题意得:∠CAB=90°﹣60°=30°,∠CBD=90°﹣30°=60°,AB=200米,CD⊥AB,
则∠ACB=∠CBD﹣∠CAB=60°﹣30°=30°,
则BC=AB=200米,
在Rt△CBD中,CD=BC sin60°=200×=100(米).
答:河宽CD为100米.
20.解:设CE=xm,则由题意可知BE=xm,AE=(x+100)m.
在Rt△AEC中,tan∠CAE=,
即tan30°=,
∴,
3x=(x+100),
解得x=50+50=136.6,
∴CD=CE+ED=136.6+1.5=138.1≈138(m).
答:该建筑物的高度约为138m.
21.解:过A作AD⊥BC,交BC的延长线于点D,
∵A在B北偏东60°方向上,
∴∠ABD=30°,
又∵A在C北偏东30°方向上,
∴∠ACD=60°
又∵∠ABC=30°,所以∠BAC=30°,
∴∠ABD=∠BAC,所以AC=BC
∵BC=120,所以AC=120
在Rt△ACD中,∠ACD=60°,AC=120,
∴CD=60,AD=
在Rt△ABD中,∵∠ABD=30°,
∴AB=
第一组时间:
第二组时间:
因为207.84>150所以第二组先到达A处.
答:第二组先到.
22.解:有触礁危险.
理由:过点P作PD⊥AC于D.
设PD为x,在Rt△PBD中,
∠PBD=90°﹣45°=45度.
∴BD=PD=x.
在Rt△PAD中,
∵∠PAD=90°﹣60°=30°
∴AD=x
∵AD=AB+BD∴x=12+x
∴x=
∵6(+1)<18
∴渔船不改变航线继续向东航行,有触礁危险.
23.解:如图,延长CD,交AB的延长线于点E,
则∠AEC=90°,∠ACE=45°,∠ADE=60°,CD=18,
设线段AE的长为x米,
在Rt△ACE中,
∵∠ACE=45°,
∴CE=x,
在Rt△ADE中,
∵tan∠ADE=tan60°=,
∴DE=x,
∵CD=18,且CE﹣DE=CD,
∴x﹣x=18,
解得:x=27+9,
∵BE=1米,
∴AB=AE﹣BE=(26+9)(米).
答:塔AB的高度是(26+9)米.
24.解:设AF=x;
在Rt△AGF中,有GF==x,
同理在Rt△AEF中,有EF==x.
结合图形可得:GE=CD=EF﹣GF=30
即x﹣x=30,
解可得:x=15;故AB=15+
答:塔高AB为15+米.
25.解:过点A作AD⊥BC于点D,设AD=xm.
在Rt△ABD中,∵∠ADB=90°,∠BAD=30°,
∴BD=AD tan30°=x.
在Rt△ACD中,∵∠ADC=90°,∠CAD=45°,
∴CD=AD=x.
∵BD+CD=BC,
∴x+x=150,
∴x=75(3﹣)≈95.
即A点到河岸BC的距离约为95m.
