2021-2022学年京改版 八年级数学上册12.7.2 直角三角形全等的判定 课后培优练习(word版含答案)
文档属性
| 名称 | 2021-2022学年京改版 八年级数学上册12.7.2 直角三角形全等的判定 课后培优练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 421.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-21 23:17:41 | ||
图片预览

文档简介
12.7.2 直角三角形全等的判定
一、单选题
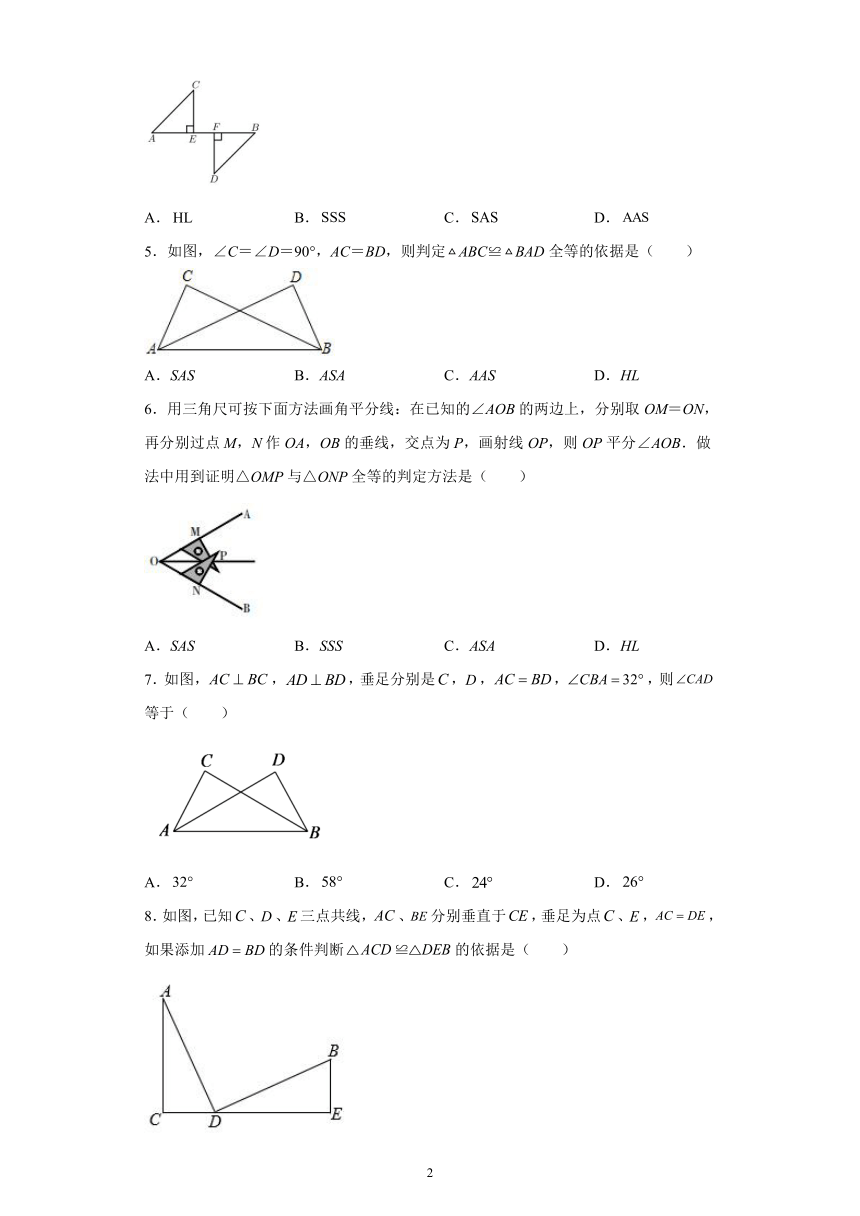
1.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
A.AE=DF B.∠A=∠D C.∠B=∠C D.AB=DC
2.如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,且AB=6cm,则△DEB的周长为( )
A.4 B.8 C.6 D.12
3.数学课上,同学们探讨利用不同画图工具画角的平分线的方法.小旭说:我用两块含30°的直角三角板就可以画角平分线.如图,取OM=ON,把直角三角板按如图所示的位置放置,两直角边交于点P,则射线OP是∠AOB的平分线,小旭这样画的理论依据是( )
A.SSA B.HL C.ASA D.SSS
4.如图,CE⊥AB,DF⊥AB,垂足分别为点E,F,且 CE=DF,AC=BD,那么 Rt△AEC≌Rt△BFD 的理由是( )
A. B. C. D.
5.如图,∠C=∠D=90°,AC=BD,则判定ABC≌BAD全等的依据是( )
A.SAS B.ASA C.AAS D.HL
6.用三角尺可按下面方法画角平分线:在已知的∠AOB的两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP,则OP平分∠AOB.做法中用到证明△OMP与△ONP全等的判定方法是( )
A.SAS B.SSS C.ASA D.HL
7.如图,,,垂足分别是,,,,则等于( )
A. B. C. D.
8.如图,已知、、三点共线,、分别垂直于,垂足为点、,,如果添加的条件判断的依据是( )
A. B. C. D.
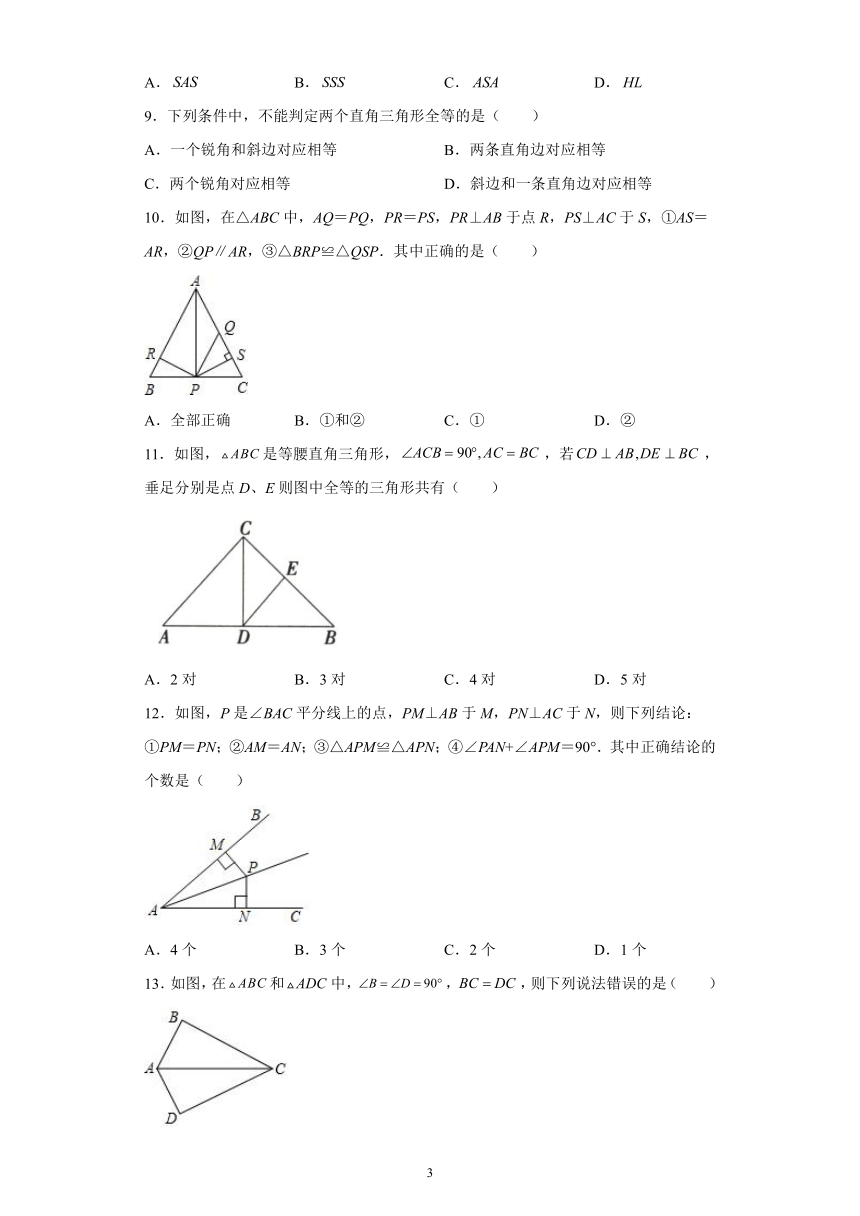
9.下列条件中,不能判定两个直角三角形全等的是( )
A.一个锐角和斜边对应相等 B.两条直角边对应相等
C.两个锐角对应相等 D.斜边和一条直角边对应相等
10.如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于S,①AS=AR,②QP∥AR,③△BRP≌△QSP.其中正确的是( )
A.全部正确 B.①和② C.① D.②
11.如图,是等腰直角三角形,,若,垂足分别是点D、E则图中全等的三角形共有( )
A.2对 B.3对 C.4对 D.5对
12.如图,P是∠BAC平分线上的点,PM⊥AB于M,PN⊥AC于N,则下列结论:①PM=PN;②AM=AN;③△APM≌△APN;④∠PAN+∠APM=90°.其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
13.如图,在和中,,,则下列说法错误的是( )
A. B. C.平分 D.平分
二、填空题
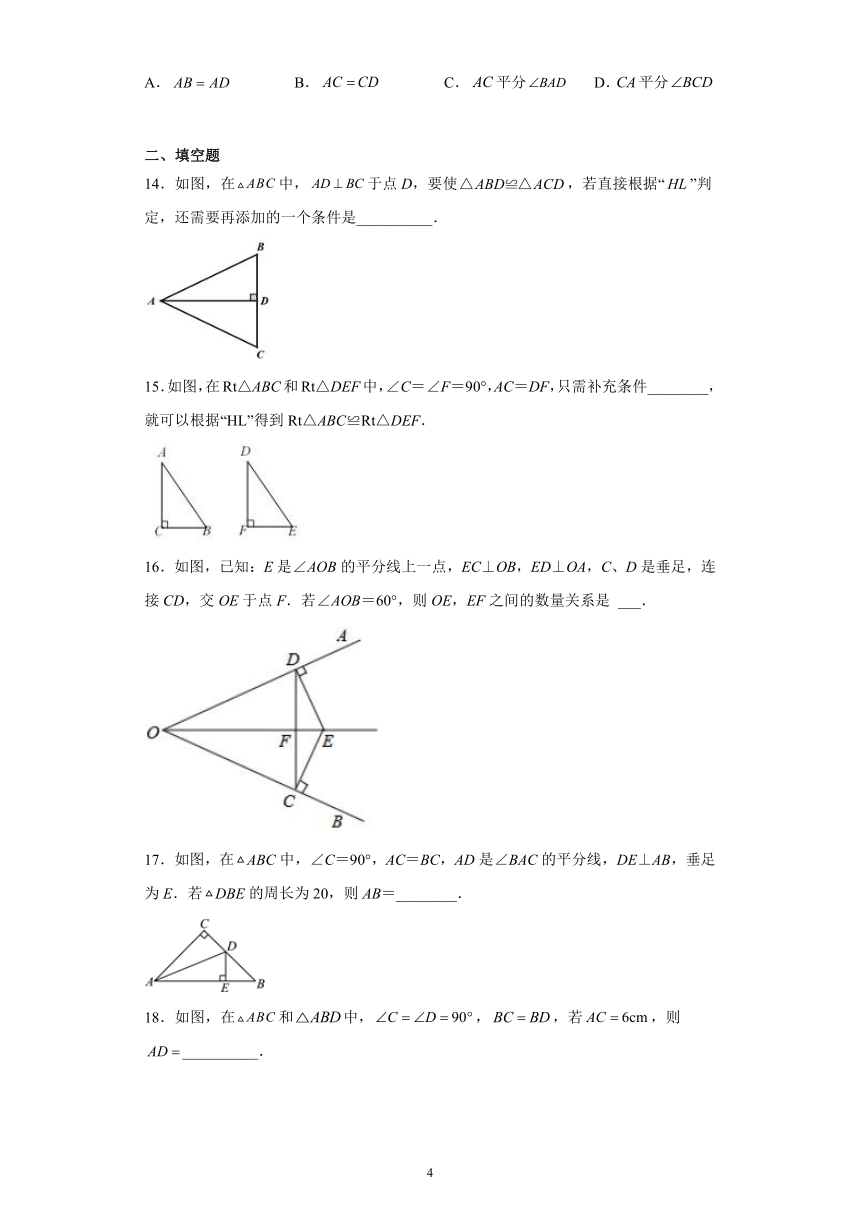
14.如图,在中,于点D,要使,若直接根据“”判定,还需要再添加的一个条件是__________.
15.如图,在Rt△ABC和Rt△DEF中,∠C=∠F=90°,AC=DF,只需补充条件________,就可以根据“HL”得到Rt△ABC≌Rt△DEF.
16.如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,交OE于点F.若∠AOB=60°,则OE,EF之间的数量关系是 ___.
17.如图,在ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.若DBE的周长为20,则AB=________.
18.如图,在和中,,,若,则__________.
三、解答题
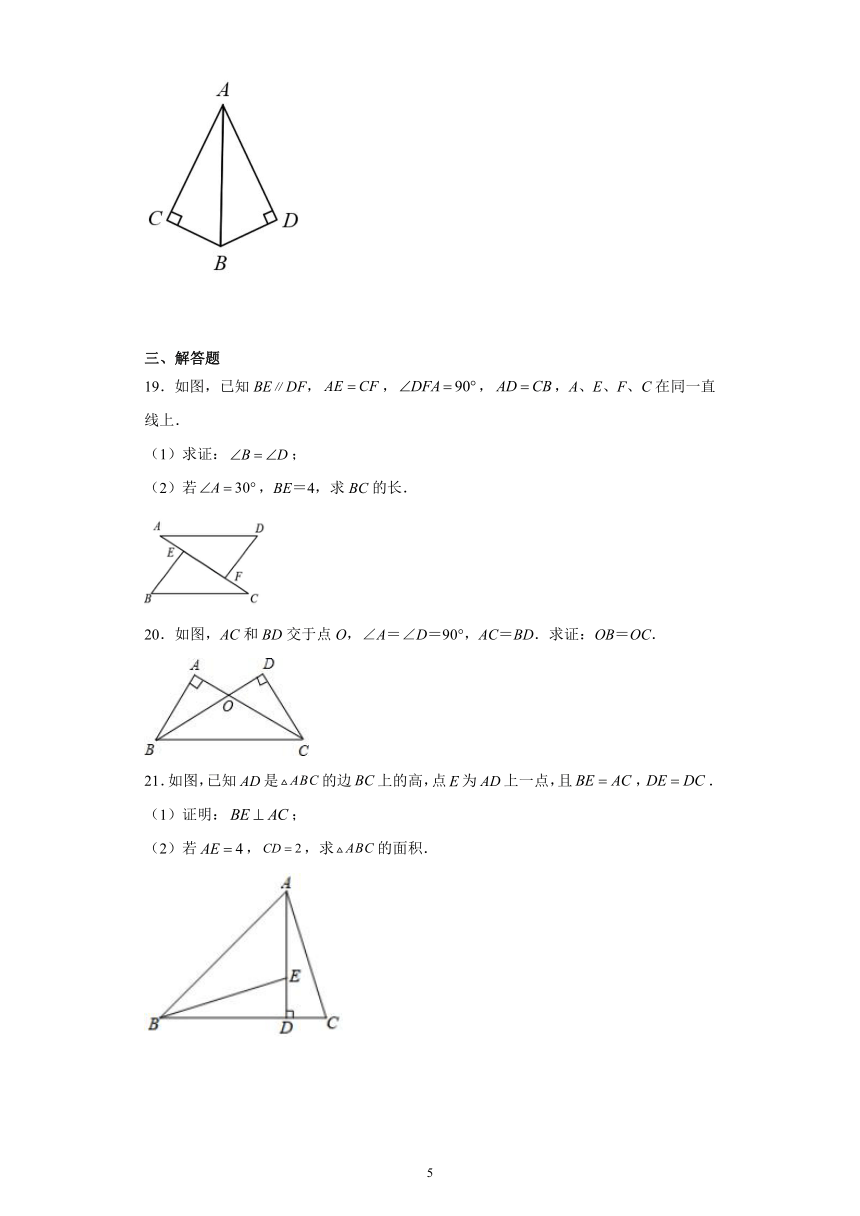
19.如图,已知BEDF,,,,A、E、F、C在同一直线上.
(1)求证:;
(2)若,BE=4,求BC的长.
20.如图,AC和BD交于点O,∠A=∠D=90°,AC=BD.求证:OB=OC.
21.如图,已知是的边上的高,点为上一点,且,.
(1)证明:;
(2)若,,求的面积.
参考答案
1.D
解:添加的条件是AB=CD;理由如下:
∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△ABE和Rt△DCF中,
,
∴ (HL).
故选:D.
2.C
解:∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴CD=DE,
在△ACD和△AED中,,
∴△ACD≌△AED(HL),
∴AC=AE,
∴△DEB的周长=BD+DE+BE,
=BD+CD+BE,
=BC+BE,
=AC+BE,
=AE+BE,
=AB,
∵AB=6cm,
∴△DEB的周长为6cm.
故选:C.
3.B
解:根据题意可得,,,
根据全等三角形的判定方法可得
故选B
4.A
证明:在Rt△ACE与Rt△BDF中,
∵AE=BF,AC=BD,
∴Rt△ACE≌Rt△BDF(HL).
故选:A.
5.D
解:∵∠C=∠D=90°,
∴△ABC和△BAD均为直角三角形
在Rt△ABC和Rt△BAD中,
,
∴Rt△ABC≌Rt△BAD(HL).
故选:D.
6.D
解:∵OM=ON,OP=OP,∠OMP=∠ONP=90°,
∴△OPM≌△OPN
所用的判定定理是HL.
故选D.
7.D
证明:,,
,
在和中,
,
,
∴,
在中,,
∴,
∴,
故选:D.
8.D
解:∵、分别垂直于,
∴,
∵,,
∴利用HL证明,
故选:D.
9.C
解:A、若一个锐角和斜边分别对应相等,可用AAS证这两个直角三角形全等,故选项说法正确,不符合题意;
B、若两条直角边对应相等,可用SAS证这两个直角三角形全等,故选项说法正确,不符合题意;
C、若两个锐角对应相等,不能证这两个直角三角形全等,故选项说法错误,符合题意;
D、若斜边和一条直角边对应相等,可用HL证这两个直角三角形全等,故选项说法正确,不符合题意;
故选:C.
10.B
解:①∵PR⊥AB,PS⊥AC,垂足分别为R、S,PR=PS.
∴AP为∠BAC的角平分线,
在△APR与△APS中,
,
∴△APR≌△APS(HL),
∴AR=AS,故本小题正确;
②∵AP为∠BAC的角平分线,
∴∠RAP=∠QAP,
∵AQ=PQ,
∴∠QAP=∠QPA,
∴∠RAP=∠QPA,
∴QP∥AR,故本小题正确;
③△BRP与△QSP只有一组边PR=PS,一组角∠PSQ=∠PRB=90°,
全等的条件不够,没法证明其全等,故本小题错误.
综上所述,①②正确.
故选:B.
11.A
∵,,,,
∴,
同理可证明.
故选A.
12.A
解:∵P是∠BAC平分线上的点,PM⊥AB于M,PN⊥AC于N,
∴PM=PN,故①正确
在Rt△APM和Rt△APN中
,
∴Rt△APM≌Rt△APN(HL),故③正确,
∴AM=AN,故②正确,
∴∠APM=∠APN,
∵∠PAN+∠APN=90°,
∴∠PAN+∠APM=90°,故④正确,
终上所述:正确的有4个.
故选:A.
13.B
解:∵∠B=∠D=90°,
∴△ABC和△ADC是直角三角形,
在Rt△ABC和Rt△ADC中,
,
∴Rt△ABC≌Rt△ADC(HL),
∴AB=AD,AC=AC,∠BAC=∠DAC,∠BCA=∠DCA,
即AC平分∠BAD,CA平分∠BCD,
故B说法错误,符合题意.
故选:B.
14.
解:还需要添加的条件是,
∵于D,
∴,
在和中,
∴,
故答案为:.
15.AB=DE
解:∵△ABC和△DEF均为直角三角形,且AC=DF,
∴需要增加它们的斜边对应相等即可利用“HL”定理,即:AB=DE;
故答案为:AB=DE.
16.
∠AOB=60°,OE是∠AOB的平分线
又 EC⊥OB,ED⊥OA,
在与中
在的垂直平分线上
即
故答案为:.
17.20
解:∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,
又
∴△ACD≌△AED,
∴CD=DE,AE=AC,
∴△DBE的周长
=DE+EB+DB
=CD+DB+EB
=BC+EB
=AC+EB
=AE+EB
=AB
=20cm.
故答案为:20.
18.
证明:在Rt△CAB和Rt△DAB中,
,
∴Rt△CAB≌Rt△DAB(HL).
∴AD=AC=6.
故答案为.
19.(1)见解析;(2)8
(1)证明:∵,,
,
,
,
即,
在和中,
,
,
;
(2)解:∵,,
∴,
,,,
.
20.证明见解析.
证明:∵∠A=∠D=90°,
在Rt△BAC与Rt△CDB中,,
∴Rt△BAC≌Rt△CDB(HL),
∴∠ACB=∠DBC,
∴OB=OC.
21.(1)证明见解析;(2).
(1)证明:延长与交于点,
∵是的边上的高,
,
在和中,
,
,
,
∵∠BED=∠AEF
,
,
∴,
即.
(2)解:由(1)可得,
,,
而,
,
,
,
即的面积为.
一、单选题
1.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
A.AE=DF B.∠A=∠D C.∠B=∠C D.AB=DC
2.如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,且AB=6cm,则△DEB的周长为( )
A.4 B.8 C.6 D.12
3.数学课上,同学们探讨利用不同画图工具画角的平分线的方法.小旭说:我用两块含30°的直角三角板就可以画角平分线.如图,取OM=ON,把直角三角板按如图所示的位置放置,两直角边交于点P,则射线OP是∠AOB的平分线,小旭这样画的理论依据是( )
A.SSA B.HL C.ASA D.SSS
4.如图,CE⊥AB,DF⊥AB,垂足分别为点E,F,且 CE=DF,AC=BD,那么 Rt△AEC≌Rt△BFD 的理由是( )
A. B. C. D.
5.如图,∠C=∠D=90°,AC=BD,则判定ABC≌BAD全等的依据是( )
A.SAS B.ASA C.AAS D.HL
6.用三角尺可按下面方法画角平分线:在已知的∠AOB的两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP,则OP平分∠AOB.做法中用到证明△OMP与△ONP全等的判定方法是( )
A.SAS B.SSS C.ASA D.HL
7.如图,,,垂足分别是,,,,则等于( )
A. B. C. D.
8.如图,已知、、三点共线,、分别垂直于,垂足为点、,,如果添加的条件判断的依据是( )
A. B. C. D.
9.下列条件中,不能判定两个直角三角形全等的是( )
A.一个锐角和斜边对应相等 B.两条直角边对应相等
C.两个锐角对应相等 D.斜边和一条直角边对应相等
10.如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于S,①AS=AR,②QP∥AR,③△BRP≌△QSP.其中正确的是( )
A.全部正确 B.①和② C.① D.②
11.如图,是等腰直角三角形,,若,垂足分别是点D、E则图中全等的三角形共有( )
A.2对 B.3对 C.4对 D.5对
12.如图,P是∠BAC平分线上的点,PM⊥AB于M,PN⊥AC于N,则下列结论:①PM=PN;②AM=AN;③△APM≌△APN;④∠PAN+∠APM=90°.其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
13.如图,在和中,,,则下列说法错误的是( )
A. B. C.平分 D.平分
二、填空题
14.如图,在中,于点D,要使,若直接根据“”判定,还需要再添加的一个条件是__________.
15.如图,在Rt△ABC和Rt△DEF中,∠C=∠F=90°,AC=DF,只需补充条件________,就可以根据“HL”得到Rt△ABC≌Rt△DEF.
16.如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,交OE于点F.若∠AOB=60°,则OE,EF之间的数量关系是 ___.
17.如图,在ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.若DBE的周长为20,则AB=________.
18.如图,在和中,,,若,则__________.
三、解答题
19.如图,已知BEDF,,,,A、E、F、C在同一直线上.
(1)求证:;
(2)若,BE=4,求BC的长.
20.如图,AC和BD交于点O,∠A=∠D=90°,AC=BD.求证:OB=OC.
21.如图,已知是的边上的高,点为上一点,且,.
(1)证明:;
(2)若,,求的面积.
参考答案
1.D
解:添加的条件是AB=CD;理由如下:
∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△ABE和Rt△DCF中,
,
∴ (HL).
故选:D.
2.C
解:∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴CD=DE,
在△ACD和△AED中,,
∴△ACD≌△AED(HL),
∴AC=AE,
∴△DEB的周长=BD+DE+BE,
=BD+CD+BE,
=BC+BE,
=AC+BE,
=AE+BE,
=AB,
∵AB=6cm,
∴△DEB的周长为6cm.
故选:C.
3.B
解:根据题意可得,,,
根据全等三角形的判定方法可得
故选B
4.A
证明:在Rt△ACE与Rt△BDF中,
∵AE=BF,AC=BD,
∴Rt△ACE≌Rt△BDF(HL).
故选:A.
5.D
解:∵∠C=∠D=90°,
∴△ABC和△BAD均为直角三角形
在Rt△ABC和Rt△BAD中,
,
∴Rt△ABC≌Rt△BAD(HL).
故选:D.
6.D
解:∵OM=ON,OP=OP,∠OMP=∠ONP=90°,
∴△OPM≌△OPN
所用的判定定理是HL.
故选D.
7.D
证明:,,
,
在和中,
,
,
∴,
在中,,
∴,
∴,
故选:D.
8.D
解:∵、分别垂直于,
∴,
∵,,
∴利用HL证明,
故选:D.
9.C
解:A、若一个锐角和斜边分别对应相等,可用AAS证这两个直角三角形全等,故选项说法正确,不符合题意;
B、若两条直角边对应相等,可用SAS证这两个直角三角形全等,故选项说法正确,不符合题意;
C、若两个锐角对应相等,不能证这两个直角三角形全等,故选项说法错误,符合题意;
D、若斜边和一条直角边对应相等,可用HL证这两个直角三角形全等,故选项说法正确,不符合题意;
故选:C.
10.B
解:①∵PR⊥AB,PS⊥AC,垂足分别为R、S,PR=PS.
∴AP为∠BAC的角平分线,
在△APR与△APS中,
,
∴△APR≌△APS(HL),
∴AR=AS,故本小题正确;
②∵AP为∠BAC的角平分线,
∴∠RAP=∠QAP,
∵AQ=PQ,
∴∠QAP=∠QPA,
∴∠RAP=∠QPA,
∴QP∥AR,故本小题正确;
③△BRP与△QSP只有一组边PR=PS,一组角∠PSQ=∠PRB=90°,
全等的条件不够,没法证明其全等,故本小题错误.
综上所述,①②正确.
故选:B.
11.A
∵,,,,
∴,
同理可证明.
故选A.
12.A
解:∵P是∠BAC平分线上的点,PM⊥AB于M,PN⊥AC于N,
∴PM=PN,故①正确
在Rt△APM和Rt△APN中
,
∴Rt△APM≌Rt△APN(HL),故③正确,
∴AM=AN,故②正确,
∴∠APM=∠APN,
∵∠PAN+∠APN=90°,
∴∠PAN+∠APM=90°,故④正确,
终上所述:正确的有4个.
故选:A.
13.B
解:∵∠B=∠D=90°,
∴△ABC和△ADC是直角三角形,
在Rt△ABC和Rt△ADC中,
,
∴Rt△ABC≌Rt△ADC(HL),
∴AB=AD,AC=AC,∠BAC=∠DAC,∠BCA=∠DCA,
即AC平分∠BAD,CA平分∠BCD,
故B说法错误,符合题意.
故选:B.
14.
解:还需要添加的条件是,
∵于D,
∴,
在和中,
∴,
故答案为:.
15.AB=DE
解:∵△ABC和△DEF均为直角三角形,且AC=DF,
∴需要增加它们的斜边对应相等即可利用“HL”定理,即:AB=DE;
故答案为:AB=DE.
16.
∠AOB=60°,OE是∠AOB的平分线
又 EC⊥OB,ED⊥OA,
在与中
在的垂直平分线上
即
故答案为:.
17.20
解:∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,
又
∴△ACD≌△AED,
∴CD=DE,AE=AC,
∴△DBE的周长
=DE+EB+DB
=CD+DB+EB
=BC+EB
=AC+EB
=AE+EB
=AB
=20cm.
故答案为:20.
18.
证明:在Rt△CAB和Rt△DAB中,
,
∴Rt△CAB≌Rt△DAB(HL).
∴AD=AC=6.
故答案为.
19.(1)见解析;(2)8
(1)证明:∵,,
,
,
,
即,
在和中,
,
,
;
(2)解:∵,,
∴,
,,,
.
20.证明见解析.
证明:∵∠A=∠D=90°,
在Rt△BAC与Rt△CDB中,,
∴Rt△BAC≌Rt△CDB(HL),
∴∠ACB=∠DBC,
∴OB=OC.
21.(1)证明见解析;(2).
(1)证明:延长与交于点,
∵是的边上的高,
,
在和中,
,
,
,
∵∠BED=∠AEF
,
,
∴,
即.
(2)解:由(1)可得,
,,
而,
,
,
,
即的面积为.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
