人教版2021-2022学年数学九年级下册26.1 反比例函数 课时练习(word版、含解析)
文档属性
| 名称 | 人教版2021-2022学年数学九年级下册26.1 反比例函数 课时练习(word版、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 274.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-21 20:17:50 | ||
图片预览




文档简介
第二十六章《反比例函数》
26.1反比例函数 专题练习
一、选择题:
1.下列点在反比例数的图象上的是( )
A. B. C. D.
2.下面说法正确的是( )
A.如果,那么x与y成反比例
B.一种商品涨价25%,要恢复原价,就要降价25%
C.圆锥体的体积等于圆柱体的体积的
D.华为公司生产的一种微型芯片长0.5米,画在一副图上长5厘米,这幅图的比例是1:100
3.当三角形的面积S一定时,三角形的底a是底边上高h的( )
A.正比例函数 B.反比例函数 C.一次函数 D.不确定
4.在下列函数中表示y关于x 的反比例函数的是( )
A.y=2x B. C. D.
5.下列四个表格表示的变量关系中,变量y是x的反比例函数的是( )
A.
B.
C.
D.
6.已知点A(1,2021)在反比例函数的图象上,则k的值是( )
A.2021 B.-2021 C.1 D.-1
7.已知函数,当函数值为3时,自变量x的值为( )
A.﹣2 B.﹣ C.﹣2或﹣ D.﹣2或﹣
二、填空题:
8.如果函数为反比例函数,则m的值是_____.
9.已知y与x成反比例,且当时,,那么当时,_____.
10.已知点P(a,b)是反比例函数图像上异于点(-1,-1)的一个动点,则=_________.
11.已知反比例函数,当,且时,自变量的取值范围为____________.
三、解答题:
12.用函数解析式表示下列问题中变量间的对应关系:
(1)一个游泳池的容积为,游泳池注满水所用时间t(单位:h)随注水速度v(单位:)的变化而变化;
(2)某长方体的体积为,长方体的高h(单位:)随底面积S(单位:)的变化而变化;
(3)一个物体重,物体对地面的压强p(单位:)随物体与地面的接触面积S(单位:)的变化而变化.
13.已知是反比例函数,且该函数图象的两个分支分布在第二、四象限,求m的值.
14.已知的图象是双曲线,且在第二、四象限,
(1)求的值.
(2)若点(-2,)、(-1,)、(1,)都在双曲线上,试比较、、的大小.
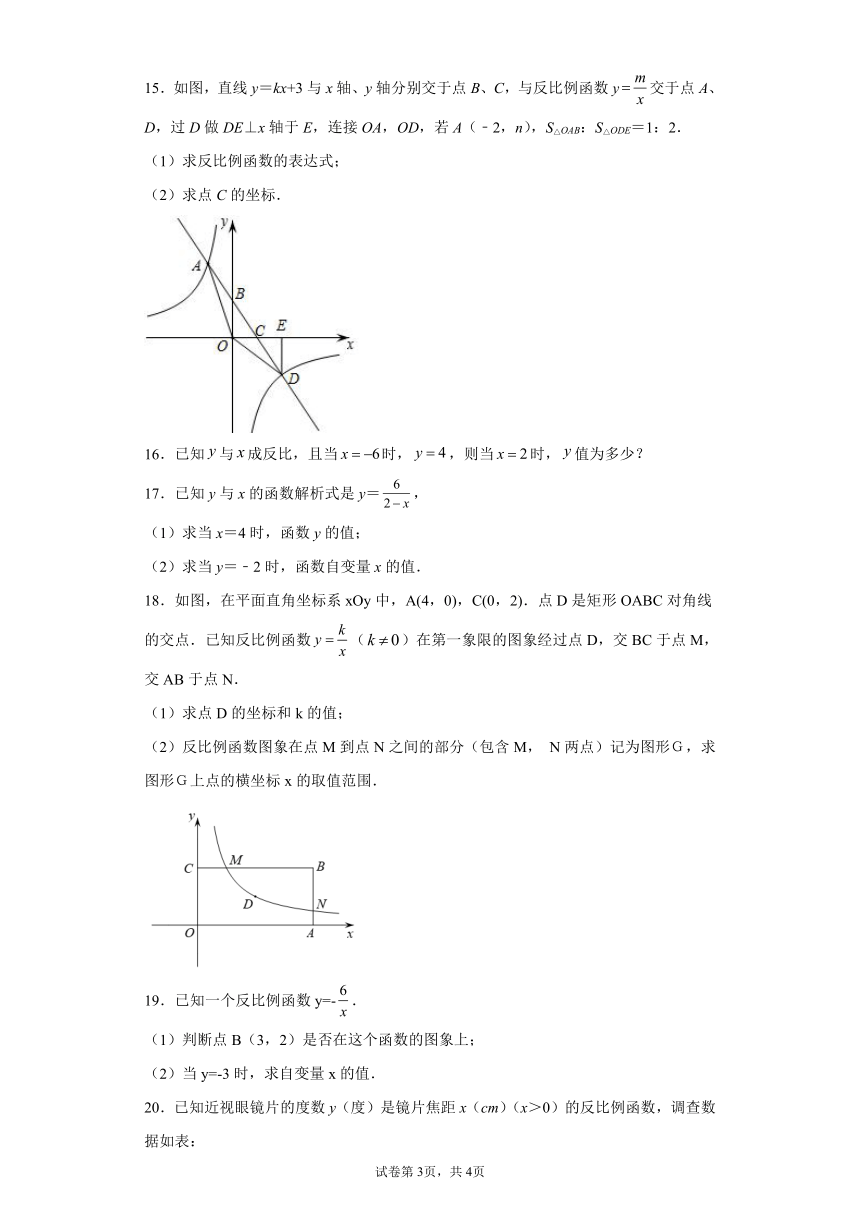
15.如图,直线y=kx+3与x轴、y轴分别交于点B、C,与反比例函数y交于点A、D,过D做DE⊥x轴于E,连接OA,OD,若A(﹣2,n),S△OAB:S△ODE=1:2.
(1)求反比例函数的表达式;
(2)求点C的坐标.
16.已知与成反比,且当时,,则当时,值为多少?
17.已知y与x的函数解析式是y=,
(1)求当x=4时,函数y的值;
(2)求当y=﹣2时,函数自变量x的值.
18.如图,在平面直角坐标系xOy中,A(4,0),C(0,2).点D是矩形OABC对角线的交点.已知反比例函数()在第一象限的图象经过点D,交BC于点M,交AB于点N.
(1)求点D的坐标和k的值;
(2)反比例函数图象在点M到点N之间的部分(包含M, N两点)记为图形G,求图形G上点的横坐标x的取值范围.
19.已知一个反比例函数y=-.
(1)判断点B(3,2)是否在这个函数的图象上;
(2)当y=-3时,求自变量x的值.
20.已知近视眼镜片的度数y(度)是镜片焦距x(cm)(x>0)的反比例函数,调查数据如表:
眼镜片度数y(度) 400 625 800 1000 … 1250
镜片焦距x(cm) 25 16 12.5 10 … 8
(1)求y与x的函数表达式;
(2)若近视眼镜镜片的度数为500度,求该镜片的焦距.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.A
【来源】山西省实验中学2021-2022学年九年级上学期期中数学试题
【分析】
反比例上的点坐标符合解析式,即,分别把点A、B、C、D坐标代入解析式中即可解题.
【详解】
解:反比例上的点坐标符合解析式,即,,
仅A符合题意,
故选:A.
【点睛】
本题考查反比例函数图象上点的坐标特征,是基础考点,掌握相关知识是解题关键.
2.A
【来源】广东省深圳市福田区红岭中学石厦校区2020-2021学年七年级上学期开学数学试题
【分析】
根据成反比例、销售问题、圆柱体与圆锥体的体积及比例的关系即可开依次判断.
【详解】
A. 如果,
则,x与y成反比例,正确;
B. 设原价为100元,一种商品涨价25%,则为100×(1+25%)=125
要恢复原价,设降价x,则125×(1-x)=100
解得x=20%
故要降价20%,故错误;
C.圆锥体的体积等于等底等高的圆柱体的体积的,故错误;
D. 华为公司生产的一种微型芯片长0.5米,画在一副图上长5厘米,这幅图的比例是
1:10,故错误.
故选A
【点睛】
此题主要考查反比例函数、销售问题、圆柱体与圆锥体的体积及比例的关系,解答此题的关键是,根据所给的选项,运用相关的知识,一一做出判断即可.
3.B
【来源】【冀教版】九年级上册第二十七章 反比例函数 27.1 反比例函数
【分析】
根据题意列出函数关系式,再根据反比例函数的定义判断即可
【详解】
解:∵,三角形的面积S一定;
∴三角形的底a是底边上高h的反比例函数;
故选:B
【点睛】
本题考查了反比例函数的定义,重点是掌握反比例函数解析式的一般式.
4.B
【来源】广西壮族自治区崇左市江州区2021-2022学年九年级上学期期中数学试题
【分析】
反比例函数解析式的一般形式为y=(k≠0),据此判断即可.
【详解】
解:A、是正比例函数,故本选项错误;
B、符合反比例函数的定义,故本选项正确;
C、是关于(x-1)的反比例函数,故本选项错误;
D、是关于x2的反比例函数,故本选项错误;
故选:B.
【点睛】
本题考查了反比例函数的定义,反比例函数解析式的一般形式为y=(k≠0),也可转化为y=kx-1(k≠0)的形式.
5.C
【来源】江苏省南京师范大学附属中学新城初级中学2020-2021学年八年级下学期期末数学试题
【分析】
判断一个函数是否是反比例函数,首先看看两个变量是否具有反比例关系,然后根据反比例函数的意义去判断,即两个变量的乘积为非零常数k.
【详解】
解:A.x与y的乘积不全都相等,故变量y不是x的反比例函数,不合题意;
B.x与y的乘积不全都相等,故变量y不是x的反比例函数,不合题意;
C.x与y的乘积全都等于﹣6,故变量y是x的反比例函数,符合题意;
D.x与y的乘积不全都相等,故变量y不是x的反比例函数,不合题意;
故选:C.
【点睛】
本题考查反比例函数的定义,利用反比例函数的定义进行判断是解题的关键.
6.A
【来源】湖南省永州市道县2021-2022学年九年级上学期期中数学试题
【分析】
将点的坐标代入,然后求解即可.
【详解】
解:点A(1,2021)在反比例函数的图象上,
.
故选:A.
【点睛】
本题考查了反比例函数图象上点的坐标特征,反比例函数图象上所有点的坐标均满足该函数的解析式.
7.A
【来源】四川省德阳市2020年中考数学试题
【分析】
根据分段函数的解析式分别计算,即可得出结论.
【详解】
解:若x<2,当y=3时,﹣x+1=3,
解得:x=﹣2;
若x≥2,当y=3时,﹣=3,
解得:x=﹣,不合题意舍去;
∴x=﹣2,
故选:A.
【点睛】
本题考查了反比例函数的性质、一次函数的图象上点的坐标特征;根据分段函数进行分段求解是解题的关键.
8.1
【来源】湖南省娄底市新化县东方文武学校2021-2022学年九年级上学期期中数学试题
【分析】
根据反比例函数的定义.即(k≠0),只需令即可.
【详解】
∵是反比例函数,
∴,
∴,
故答案为:1.
【点睛】
本题考查了反比例函数的定义,重点是将一般式(k≠0)转化为(k≠0)的形式.
9.-2
【来源】【冀教版】九年级上册第二十七章 反比例函数 27.1 反比例函数
【分析】
先求出反比例函数解析式,再代入求值即可.
【详解】
设,
把,代入得
,
解得,
则函数的表达式是,
把代入得.
故答案为-2.
【点睛】
本题考查了待定系数法求反比例解析式,解题的关键是正确设出反比例函数解析式.
10.2
【来源】江苏省苏州市高新区2020~2021学年下学期八年级数学期末试卷
【分析】
利用反比例函数图象上点的坐标性质得出,再利用分式的混合运算法则求出即可.
【详解】
解:点是反比例函数图象上异于点的一个动点,
,
.
故答案为2.
【点睛】
此题主要考查了反比例函数图象上点的坐标特征以及分式的混合运算,正确化简分式是解题关键.
11.x<-9或x>0
【来源】【新东方】初中数学1162
【分析】
求出y=时x的值,再根据反比例函数的性质求解即可.
【详解】
解:在中,-12<0,
∴反比例函数经过第二、四象限,
令,得:x=-9,
当x>0时,y<0<,
当x<0时,若,则x<-9,
∴x的取值范围是:x<-9或x>0,
故答案为:x<-9或x>0.
【点睛】
本题考查了反比例函数的图像和性质,正确分类讨论是解题关键.
12.(1);(2);(3).
【来源】【人教版课时练习】九年级下册数学第二十六章 反比例函数 26.1.1 反比例函数
【分析】
(1)根据游泳池的容积=游泳池注满水所用时间×注水速度解答即可;
(2)根据长方体的体积=长方体的底面积×高求解即可;
(3)根据物体对地面的压强=物体重量÷物体与地面的接触面积解答即可.
【详解】
解:(1)根据vt=2000得:游泳池注满水所用时间;
(2)根据1000=Sh得:长方体的高;
(3)根据题意,物体对地面的压强.
【点睛】
本题考查反比例函数的应用,正确得出函数关系式是解答的关键.
13.
【来源】福建省泉州市晋江市2019-2020学年八年级下学期期末数学试题
【分析】
直接利用反比例函数的定义得出m,再利用反比例函数图象分布在第二、四象限,得出m的值.
【详解】
解:∵是反比例函数,
∴,
∴,
解得:,
∵该函数图象的两个分支分布在第二、四象限,
∴,
∴.
【点睛】
此题主要考查了反比例函数的定义与性质,解题的关键是正确掌握反比例函数图象分布的规律.
14.(1)1;(2)
【来源】专题20 反比例函数-2021-2022学年九年级数学上册链接教材精准变式练(北师大版)
【分析】
(1)根据反比例函数的定义与性质列式求解;
(2)根据反比例函数的增减性解答即可.
【详解】
解:(1)由已知条件可知:,
∴;
(2)由(1)得此函数解析式为:.
∵ (-2,)、(-1,)在第二象限,-2<-1,
∴ .
∵(1,)在第四象限,
∴.
∴.
【点睛】
本题考查了反比例函数的的定义,以及反比例函数的图象与性质,反比例函数(k是常数,k≠0)的图象是双曲线,当k>0,反比例函数图象的两个分支在第一、三象限,在每一象限内,y随x的增大而减小;当 k<0,反比例函数图象的两个分支在第二、四象限,在每一象限内,y随x的增大而增大.
15.(1),(2)点C(2,0).
【来源】山东省青岛市市南区2020-2021学年九年级上学期期末数学试题
【分析】
(1)根据题意求出点B,继而求得S△ODE=6,再设D(xD,yD)可列得S△ODE,整理即可求解;
(2)根据题意求得A(-2,6),将点A代入直线y=kx+3易得直线解析式,令,即可求解点C坐标.
【详解】
(1)∵直线y=kx+3与x轴、y轴分别交于点B、C,
当,,
即B(0,3),
∵A(﹣2,n),
∴S△OAB= ,
∵S△OAB:S△ODE=1:2.
∴S△ODE=6,
∵点D在反比例函数y图象上,
则设D(xD,yD),
∴S△ODE,
∵
∴S△ODE,
∴
∴,
∴,
(2)∵点A(﹣2,n)在反比例函数图象上,
∴,
即A(-2,6),
将点A代入直线y=kx+3,得:,
解得:,
∴,
当时,,
∴
即点C(2,0)
【点睛】
本题考查反比例函数与一次函数,解题的关键是熟练掌握反比例函数图象上点的特点,利用数形结合的思想.
16.-12
【来源】专题20 反比例函数-2021-2022学年九年级数学上册链接教材精准变式练(北师大版)
【分析】
根据题意,设,进而求得,再根据的值求得的值.
【详解】
解:设,当时,,
所以,则=-24,
所以有.
当时,.
【点睛】
本题考查了反比例函数解析式,根据题意求得是解题的关键.
17.(1)-3;(2)x=5
【来源】沪科版2021-2022学年九年级数学上册第21章 二次函数与反比例函数专题04 反比例函数的概念、图像与性质(强化-基础)
【分析】
(1)把x=4代入解析式,即可求得y的值;
(2)y= 2代入解析式,即可求得自变量x的值.
【详解】
解:(1)当x=4时,函数y=;
(2)当y=﹣2时,则﹣2=,
解得x=5.
【点睛】
本题考查反比例函数图象上点的坐标特征,反比例函数的图象上点的坐标适合解析式是解题的关键.
18.(1)D(2,1);k=2;(2)
【来源】河北省承德市丰宁满族自治县2020-2021学年九年级上学期期末数学试题
【分析】
(1)根据矩形的性质即可求解D的坐标,从而求解k;
(2)结合矩形的性质可得到M的纵坐标,以及N的横坐标,从而得出结论.
【详解】
(1)∵点D是矩形OABC的对角线交点,
∴点D是矩形OABC的对角线AC的中点,
又∵A(4,0),C(0,2),
∴点D的坐标为(2,1),
∵反比例函数的图象经过点D,
∴,解得:k=2;
(2)由题意可得:点M的纵坐标为2,点N的横坐标为4.
∵点M在反比例函数的图象上,
∴点M的坐标为(1,2),
∴.
【点睛】
本题考查矩形的性质,求反比例函数的解析式以及反比例函数图像上点的特征,熟练掌握矩形的性质,理解反比例函数图象上点的特征是解题关键.
19.(1)点不在函数的图象上;(2).
【来源】福建省2019-2020学年九年级上学期第二次月考数学试题
【分析】
(1)根据点的坐标满足函数解析式,则点在函数图象上,否则不在函数图象上,可得答案;
(2)将y=-3代入函数解析式,即可求得x.
【详解】
解:(1)当时,,
∴点不在函数的图象上;
(2)函数的解析式为,
当时,,
∴.
【点睛】
本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.
20.(1)y=;(2)20cm.
【来源】江苏省南京市秦淮区2018-2019学年八年级下学期期末数学试题
【分析】
(1)根据图表可以得到眼镜片的度数与焦距的积是一个常数,因而眼镜片度数与镜片焦距成反比例函数关系,即可求解;
(2)在解析式中,令y=500,求出x的值即可.
【详解】
解:(1)根据题意得:y与x之积恒为10000,则函数的解析式是y=;
(2)令y=500,则500=,
解得:x=20.
即该镜片的焦距是20cm.
【点睛】
本题考查了反比例函数的应用,正确理解反比例函数的特点,两个变量的积是常数,是解决本题的关键.答案第2页,共12页
答案第1页,共12页
26.1反比例函数 专题练习
一、选择题:
1.下列点在反比例数的图象上的是( )
A. B. C. D.
2.下面说法正确的是( )
A.如果,那么x与y成反比例
B.一种商品涨价25%,要恢复原价,就要降价25%
C.圆锥体的体积等于圆柱体的体积的
D.华为公司生产的一种微型芯片长0.5米,画在一副图上长5厘米,这幅图的比例是1:100
3.当三角形的面积S一定时,三角形的底a是底边上高h的( )
A.正比例函数 B.反比例函数 C.一次函数 D.不确定
4.在下列函数中表示y关于x 的反比例函数的是( )
A.y=2x B. C. D.
5.下列四个表格表示的变量关系中,变量y是x的反比例函数的是( )
A.
B.
C.
D.
6.已知点A(1,2021)在反比例函数的图象上,则k的值是( )
A.2021 B.-2021 C.1 D.-1
7.已知函数,当函数值为3时,自变量x的值为( )
A.﹣2 B.﹣ C.﹣2或﹣ D.﹣2或﹣
二、填空题:
8.如果函数为反比例函数,则m的值是_____.
9.已知y与x成反比例,且当时,,那么当时,_____.
10.已知点P(a,b)是反比例函数图像上异于点(-1,-1)的一个动点,则=_________.
11.已知反比例函数,当,且时,自变量的取值范围为____________.
三、解答题:
12.用函数解析式表示下列问题中变量间的对应关系:
(1)一个游泳池的容积为,游泳池注满水所用时间t(单位:h)随注水速度v(单位:)的变化而变化;
(2)某长方体的体积为,长方体的高h(单位:)随底面积S(单位:)的变化而变化;
(3)一个物体重,物体对地面的压强p(单位:)随物体与地面的接触面积S(单位:)的变化而变化.
13.已知是反比例函数,且该函数图象的两个分支分布在第二、四象限,求m的值.
14.已知的图象是双曲线,且在第二、四象限,
(1)求的值.
(2)若点(-2,)、(-1,)、(1,)都在双曲线上,试比较、、的大小.
15.如图,直线y=kx+3与x轴、y轴分别交于点B、C,与反比例函数y交于点A、D,过D做DE⊥x轴于E,连接OA,OD,若A(﹣2,n),S△OAB:S△ODE=1:2.
(1)求反比例函数的表达式;
(2)求点C的坐标.
16.已知与成反比,且当时,,则当时,值为多少?
17.已知y与x的函数解析式是y=,
(1)求当x=4时,函数y的值;
(2)求当y=﹣2时,函数自变量x的值.
18.如图,在平面直角坐标系xOy中,A(4,0),C(0,2).点D是矩形OABC对角线的交点.已知反比例函数()在第一象限的图象经过点D,交BC于点M,交AB于点N.
(1)求点D的坐标和k的值;
(2)反比例函数图象在点M到点N之间的部分(包含M, N两点)记为图形G,求图形G上点的横坐标x的取值范围.
19.已知一个反比例函数y=-.
(1)判断点B(3,2)是否在这个函数的图象上;
(2)当y=-3时,求自变量x的值.
20.已知近视眼镜片的度数y(度)是镜片焦距x(cm)(x>0)的反比例函数,调查数据如表:
眼镜片度数y(度) 400 625 800 1000 … 1250
镜片焦距x(cm) 25 16 12.5 10 … 8
(1)求y与x的函数表达式;
(2)若近视眼镜镜片的度数为500度,求该镜片的焦距.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.A
【来源】山西省实验中学2021-2022学年九年级上学期期中数学试题
【分析】
反比例上的点坐标符合解析式,即,分别把点A、B、C、D坐标代入解析式中即可解题.
【详解】
解:反比例上的点坐标符合解析式,即,,
仅A符合题意,
故选:A.
【点睛】
本题考查反比例函数图象上点的坐标特征,是基础考点,掌握相关知识是解题关键.
2.A
【来源】广东省深圳市福田区红岭中学石厦校区2020-2021学年七年级上学期开学数学试题
【分析】
根据成反比例、销售问题、圆柱体与圆锥体的体积及比例的关系即可开依次判断.
【详解】
A. 如果,
则,x与y成反比例,正确;
B. 设原价为100元,一种商品涨价25%,则为100×(1+25%)=125
要恢复原价,设降价x,则125×(1-x)=100
解得x=20%
故要降价20%,故错误;
C.圆锥体的体积等于等底等高的圆柱体的体积的,故错误;
D. 华为公司生产的一种微型芯片长0.5米,画在一副图上长5厘米,这幅图的比例是
1:10,故错误.
故选A
【点睛】
此题主要考查反比例函数、销售问题、圆柱体与圆锥体的体积及比例的关系,解答此题的关键是,根据所给的选项,运用相关的知识,一一做出判断即可.
3.B
【来源】【冀教版】九年级上册第二十七章 反比例函数 27.1 反比例函数
【分析】
根据题意列出函数关系式,再根据反比例函数的定义判断即可
【详解】
解:∵,三角形的面积S一定;
∴三角形的底a是底边上高h的反比例函数;
故选:B
【点睛】
本题考查了反比例函数的定义,重点是掌握反比例函数解析式的一般式.
4.B
【来源】广西壮族自治区崇左市江州区2021-2022学年九年级上学期期中数学试题
【分析】
反比例函数解析式的一般形式为y=(k≠0),据此判断即可.
【详解】
解:A、是正比例函数,故本选项错误;
B、符合反比例函数的定义,故本选项正确;
C、是关于(x-1)的反比例函数,故本选项错误;
D、是关于x2的反比例函数,故本选项错误;
故选:B.
【点睛】
本题考查了反比例函数的定义,反比例函数解析式的一般形式为y=(k≠0),也可转化为y=kx-1(k≠0)的形式.
5.C
【来源】江苏省南京师范大学附属中学新城初级中学2020-2021学年八年级下学期期末数学试题
【分析】
判断一个函数是否是反比例函数,首先看看两个变量是否具有反比例关系,然后根据反比例函数的意义去判断,即两个变量的乘积为非零常数k.
【详解】
解:A.x与y的乘积不全都相等,故变量y不是x的反比例函数,不合题意;
B.x与y的乘积不全都相等,故变量y不是x的反比例函数,不合题意;
C.x与y的乘积全都等于﹣6,故变量y是x的反比例函数,符合题意;
D.x与y的乘积不全都相等,故变量y不是x的反比例函数,不合题意;
故选:C.
【点睛】
本题考查反比例函数的定义,利用反比例函数的定义进行判断是解题的关键.
6.A
【来源】湖南省永州市道县2021-2022学年九年级上学期期中数学试题
【分析】
将点的坐标代入,然后求解即可.
【详解】
解:点A(1,2021)在反比例函数的图象上,
.
故选:A.
【点睛】
本题考查了反比例函数图象上点的坐标特征,反比例函数图象上所有点的坐标均满足该函数的解析式.
7.A
【来源】四川省德阳市2020年中考数学试题
【分析】
根据分段函数的解析式分别计算,即可得出结论.
【详解】
解:若x<2,当y=3时,﹣x+1=3,
解得:x=﹣2;
若x≥2,当y=3时,﹣=3,
解得:x=﹣,不合题意舍去;
∴x=﹣2,
故选:A.
【点睛】
本题考查了反比例函数的性质、一次函数的图象上点的坐标特征;根据分段函数进行分段求解是解题的关键.
8.1
【来源】湖南省娄底市新化县东方文武学校2021-2022学年九年级上学期期中数学试题
【分析】
根据反比例函数的定义.即(k≠0),只需令即可.
【详解】
∵是反比例函数,
∴,
∴,
故答案为:1.
【点睛】
本题考查了反比例函数的定义,重点是将一般式(k≠0)转化为(k≠0)的形式.
9.-2
【来源】【冀教版】九年级上册第二十七章 反比例函数 27.1 反比例函数
【分析】
先求出反比例函数解析式,再代入求值即可.
【详解】
设,
把,代入得
,
解得,
则函数的表达式是,
把代入得.
故答案为-2.
【点睛】
本题考查了待定系数法求反比例解析式,解题的关键是正确设出反比例函数解析式.
10.2
【来源】江苏省苏州市高新区2020~2021学年下学期八年级数学期末试卷
【分析】
利用反比例函数图象上点的坐标性质得出,再利用分式的混合运算法则求出即可.
【详解】
解:点是反比例函数图象上异于点的一个动点,
,
.
故答案为2.
【点睛】
此题主要考查了反比例函数图象上点的坐标特征以及分式的混合运算,正确化简分式是解题关键.
11.x<-9或x>0
【来源】【新东方】初中数学1162
【分析】
求出y=时x的值,再根据反比例函数的性质求解即可.
【详解】
解:在中,-12<0,
∴反比例函数经过第二、四象限,
令,得:x=-9,
当x>0时,y<0<,
当x<0时,若,则x<-9,
∴x的取值范围是:x<-9或x>0,
故答案为:x<-9或x>0.
【点睛】
本题考查了反比例函数的图像和性质,正确分类讨论是解题关键.
12.(1);(2);(3).
【来源】【人教版课时练习】九年级下册数学第二十六章 反比例函数 26.1.1 反比例函数
【分析】
(1)根据游泳池的容积=游泳池注满水所用时间×注水速度解答即可;
(2)根据长方体的体积=长方体的底面积×高求解即可;
(3)根据物体对地面的压强=物体重量÷物体与地面的接触面积解答即可.
【详解】
解:(1)根据vt=2000得:游泳池注满水所用时间;
(2)根据1000=Sh得:长方体的高;
(3)根据题意,物体对地面的压强.
【点睛】
本题考查反比例函数的应用,正确得出函数关系式是解答的关键.
13.
【来源】福建省泉州市晋江市2019-2020学年八年级下学期期末数学试题
【分析】
直接利用反比例函数的定义得出m,再利用反比例函数图象分布在第二、四象限,得出m的值.
【详解】
解:∵是反比例函数,
∴,
∴,
解得:,
∵该函数图象的两个分支分布在第二、四象限,
∴,
∴.
【点睛】
此题主要考查了反比例函数的定义与性质,解题的关键是正确掌握反比例函数图象分布的规律.
14.(1)1;(2)
【来源】专题20 反比例函数-2021-2022学年九年级数学上册链接教材精准变式练(北师大版)
【分析】
(1)根据反比例函数的定义与性质列式求解;
(2)根据反比例函数的增减性解答即可.
【详解】
解:(1)由已知条件可知:,
∴;
(2)由(1)得此函数解析式为:.
∵ (-2,)、(-1,)在第二象限,-2<-1,
∴ .
∵(1,)在第四象限,
∴.
∴.
【点睛】
本题考查了反比例函数的的定义,以及反比例函数的图象与性质,反比例函数(k是常数,k≠0)的图象是双曲线,当k>0,反比例函数图象的两个分支在第一、三象限,在每一象限内,y随x的增大而减小;当 k<0,反比例函数图象的两个分支在第二、四象限,在每一象限内,y随x的增大而增大.
15.(1),(2)点C(2,0).
【来源】山东省青岛市市南区2020-2021学年九年级上学期期末数学试题
【分析】
(1)根据题意求出点B,继而求得S△ODE=6,再设D(xD,yD)可列得S△ODE,整理即可求解;
(2)根据题意求得A(-2,6),将点A代入直线y=kx+3易得直线解析式,令,即可求解点C坐标.
【详解】
(1)∵直线y=kx+3与x轴、y轴分别交于点B、C,
当,,
即B(0,3),
∵A(﹣2,n),
∴S△OAB= ,
∵S△OAB:S△ODE=1:2.
∴S△ODE=6,
∵点D在反比例函数y图象上,
则设D(xD,yD),
∴S△ODE,
∵
∴S△ODE,
∴
∴,
∴,
(2)∵点A(﹣2,n)在反比例函数图象上,
∴,
即A(-2,6),
将点A代入直线y=kx+3,得:,
解得:,
∴,
当时,,
∴
即点C(2,0)
【点睛】
本题考查反比例函数与一次函数,解题的关键是熟练掌握反比例函数图象上点的特点,利用数形结合的思想.
16.-12
【来源】专题20 反比例函数-2021-2022学年九年级数学上册链接教材精准变式练(北师大版)
【分析】
根据题意,设,进而求得,再根据的值求得的值.
【详解】
解:设,当时,,
所以,则=-24,
所以有.
当时,.
【点睛】
本题考查了反比例函数解析式,根据题意求得是解题的关键.
17.(1)-3;(2)x=5
【来源】沪科版2021-2022学年九年级数学上册第21章 二次函数与反比例函数专题04 反比例函数的概念、图像与性质(强化-基础)
【分析】
(1)把x=4代入解析式,即可求得y的值;
(2)y= 2代入解析式,即可求得自变量x的值.
【详解】
解:(1)当x=4时,函数y=;
(2)当y=﹣2时,则﹣2=,
解得x=5.
【点睛】
本题考查反比例函数图象上点的坐标特征,反比例函数的图象上点的坐标适合解析式是解题的关键.
18.(1)D(2,1);k=2;(2)
【来源】河北省承德市丰宁满族自治县2020-2021学年九年级上学期期末数学试题
【分析】
(1)根据矩形的性质即可求解D的坐标,从而求解k;
(2)结合矩形的性质可得到M的纵坐标,以及N的横坐标,从而得出结论.
【详解】
(1)∵点D是矩形OABC的对角线交点,
∴点D是矩形OABC的对角线AC的中点,
又∵A(4,0),C(0,2),
∴点D的坐标为(2,1),
∵反比例函数的图象经过点D,
∴,解得:k=2;
(2)由题意可得:点M的纵坐标为2,点N的横坐标为4.
∵点M在反比例函数的图象上,
∴点M的坐标为(1,2),
∴.
【点睛】
本题考查矩形的性质,求反比例函数的解析式以及反比例函数图像上点的特征,熟练掌握矩形的性质,理解反比例函数图象上点的特征是解题关键.
19.(1)点不在函数的图象上;(2).
【来源】福建省2019-2020学年九年级上学期第二次月考数学试题
【分析】
(1)根据点的坐标满足函数解析式,则点在函数图象上,否则不在函数图象上,可得答案;
(2)将y=-3代入函数解析式,即可求得x.
【详解】
解:(1)当时,,
∴点不在函数的图象上;
(2)函数的解析式为,
当时,,
∴.
【点睛】
本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.
20.(1)y=;(2)20cm.
【来源】江苏省南京市秦淮区2018-2019学年八年级下学期期末数学试题
【分析】
(1)根据图表可以得到眼镜片的度数与焦距的积是一个常数,因而眼镜片度数与镜片焦距成反比例函数关系,即可求解;
(2)在解析式中,令y=500,求出x的值即可.
【详解】
解:(1)根据题意得:y与x之积恒为10000,则函数的解析式是y=;
(2)令y=500,则500=,
解得:x=20.
即该镜片的焦距是20cm.
【点睛】
本题考查了反比例函数的应用,正确理解反比例函数的特点,两个变量的积是常数,是解决本题的关键.答案第2页,共12页
答案第1页,共12页
