人教版2021-2022学年数学九年级下册26.2 实际问题与反比例函数 课时练习(word版、含解析)
文档属性
| 名称 | 人教版2021-2022学年数学九年级下册26.2 实际问题与反比例函数 课时练习(word版、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 628.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-21 20:21:38 | ||
图片预览




文档简介
第二十六章《反比例函数》
26.2 实际问题与反比例函数 专题练习
一、选择题:
1.甲、乙两地相距100千米,某人开车从甲地到乙地,那么它的速度v(千米/小时)与时间t(小时)之间的函数关系用图象表示大致为( )
A. B. C. D.
2.如图,在平面直角坐示系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的横坐标分别为1,2,反比例函数的图像经过A,B两点,则菱形ABCD的边长为()
A.1 B. C.2 D.
3.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种蔬菜.上图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图像,其中BC段是双曲线(k≠0)的一部分,则当x = 16时,大棚内的温度约为( )
A.18℃ B.15.5℃ C.13.5℃ D.12℃
4.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为 B.蓄电池的电压是18V
C.当时, D.当时,
5.如图,一块长方体砖块的长、宽、高的比为,如果左视面向下放在地上,地面所受压强为,则正视面向下放在地上时,地面所受压强为( )
A. B. C. D.
6.如图,直线与双曲线交于、两点,则当时,x的取值范围是
A.或
B.或
C.或
D.
7.已知某种品牌电脑的显示器的使用寿命大约为时,这种显示器工作的天数为d(天),平均每天工作的时间为t(时),那么d与t之间的函数图象大致是( )
A. B. C. D.
8.某校科技小组进行野外考察,途中遇到一片十几米宽的湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺若干块木板,构筑成一条临时通道,木板对地面的压强风是木板面积的反比例函数,其图象如图所示,当木板压强不超过时,木板的面积应为( )
A.不大于 B.不小于 C.不大于 D.不小于
9.在矩形ABCD中,E点为AB上的一点,AB=8,AD=6,连接CE,作DF⊥CE于F点,令CE=x,DF=y,下列关于y与x的函数关系图象大致是( )
A. B.
C. D.
二、填空题:
10.若矩形的面积为2,则矩形相邻两边的长成______比例.
11.甲、乙两地相距200千米,汽车从甲地匀速行驶到乙地,汽车行驶时间关于行驶速度的函数表达式是_____.
12.码头工人每天往一艘轮船上装载20吨货物,装载完毕恰好用了10天时间.轮船到达目的地后开始卸货,记平均卸货速度为v(单位:吨/天),卸货天数为t.则v关于t的函数表达式为________;如果船上的货物8天卸载完毕,那么平均每天要卸载________吨货物.
13.近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25m,则眼镜度数与镜片焦距之间的函数关系式为________.
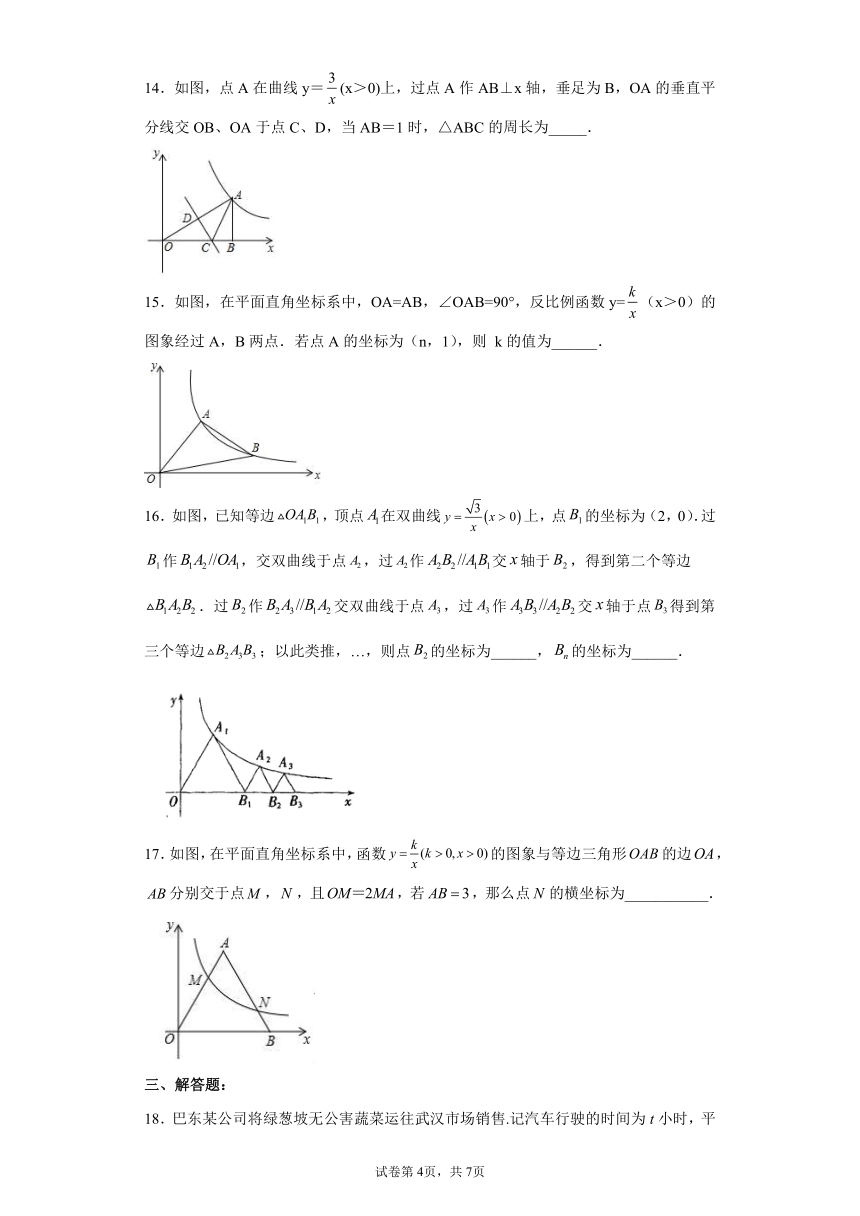
14.如图,点A在曲线y=(x>0)上,过点A作AB⊥x轴,垂足为B,OA的垂直平分线交OB、OA于点C、D,当AB=1时,△ABC的周长为_____.
15.如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y=(x>0)的图象经过A,B两点.若点A的坐标为(n,1),则 k的值为______.
16.如图,已知等边,顶点在双曲线上,点的坐标为(2,0).过作,交双曲线于点,过作交轴于,得到第二个等边.过作交双曲线于点,过作交轴于点得到第三个等边;以此类推,…,则点的坐标为______,的坐标为______.
17.如图,在平面直角坐标系中,函数的图象与等边三角形的边,分别交于点,,且,若,那么点的横坐标为___________.
三、解答题:
18.巴东某公司将绿葱坡无公害蔬菜运往武汉市场销售.记汽车行驶的时间为t小时,平均速度为u千米/小时(汽车行驶速度不能超过100千米/小时),司机根据经验,提供如下表所列一组t,u的对应值:
u(千米/小时) 50 75 80 90 95
t(小时) 12 8 7.5 6.67 6.32
(1)根据表中的数据,请你求出平均速度u关于行驶时间t的函数关系式;
(2)若蔬菜运输汽车早上8:00从巴东出发,能否在中午1:00到达武汉市场?请说明理由;
(3)长途开车要杜绝疲劳驾驶,但又要减小蔬菜长途运输的损耗. 因此,汽车到达武汉市场的行驶时间t满足7≤t≤9.5为佳,求平均速度u的取值范围.
19.根据传染病防控制度的要求,学校必须对教室定期用药熏消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物燃烧完毕后,y(毫克)与时间x(分钟)成反比例,如图所示.请根据图中所提供的信息,解答下列问题:
(1)当药物燃烧时,y关于x的函数关系式为 ,自变量x的取值范围为 ;药物燃烧后,y关于x的函数关系式为 ;
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进入教室,则从消毒开始,至少需要经过 分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于2毫克且持续时间不低于14分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
20.某空调生产厂的装配车间计划在一段时期内组装9000台空调.
(1)在这段时期内,每天组装的数量m(台/天)与组装的时间t(天)之间有怎样的函数关系?
(2)原计划用2个月时间(每月按30天计算)完成这一任务,但由于气温提前升高,厂家决定这批空调提前10天完成组装,那么装配车间每天至少要组装多少台空调?比原计划多多少?
21.某电商店铺为促销一件标价59元的商品A,制定了以下促销方案:在指定日期购买商品A(限购8件),除包邮外,享受每满240元(标价)减40元,但在收货之前不能退换,小华正好需要该商品,于是计划等到优惠日期进行购买.
(1)请求出小华每件商品实付款的均价与购买商品A的件数的关系;
(2)小华对该商品的实际需求为4件,为了追求最大优惠,小华考虑以下两种方案:
方案一:直接按店铺优惠活动进行购买,不退货;
方案二:凑单享受满减,即购买恰好享受下一级满减活动的件数,然后将超过自己需要的部分商品以实付款均价退回,但需要自行承担退货的运费(运费规则:首件10元,每多一件加4元).
若以小华的实际支出均价(实际支出均价=)为依据,请你为小华选择一个优惠的购买方案.
22.某养殖场需要定期购买饲料,已知该养殖场每天需要200千克饲料,饲料的价格为1.8元/千克,饲料的保管费与其他费用平均每天为0.05元/千克,购买饲料每次的运费为180元.
任务1:该养殖场多少天购买一次饲料才能使平均每天支付的总费用最少;
小明的分析如下:如果2天购买一次,则保管费与其他费用需支付200×0.05=10(元);如果3天购买一次,则保管费与其他费用需支付200×2×0.05+200×0.05=30(元);如果4天购买一次,则保管费与其他费用需支付200×3×0.05+200×2×0.05+200×0.05=60(元),他发现已有的数学模型不能解决这个问题,想到了用函数图象的方法解决,设x天购买一次饲料,平均每天支付的总费用为y元,下面是他解决这个问题的过程,请解答相关问题.
(1)计算得到x与y的部分对应值如下表,请补全表格;
x/天 … 2 3 4 5 6 7 8 9 10 …
Y/元 … 455.0 430.0 420.0 415.7 417.5 420.0 423.0 …
(2)在平面直角坐标系中,描出(1)中所对应的点;
(3)结合图象:养殖场 天购买一次饲料才能使平均每天支付的总费用最少.
任务2:提供饲料的公司规定,当一次购买饲料不少于2000千克时,价格可享受九折优惠,在该养殖场购买饲料时是否需要考虑这一优惠条件,简要说明理由.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.D
【来源】考点12 反比例函数—2021年《三步冲刺中考 数学》(广东专版)之第1步小题夯基础
【分析】
直接利用速度= ,进而得出函数关系式,即可得出其函数图形.
【详解】
解:∵甲、乙两地相距100千米,某人开车从甲地到乙地,
∴它的速度v(千米/小时)与时间t(小时)之间的函数关系为:v= (t>0),
则此函数关系用图象表示大致为:
.
故选:D.
【点睛】
此题考查反比例函数的实际应用,难度一般.
2.B
【来源】【万唯原创】2020年山西-面对面-选填题组5
【分析】
过点A作x轴的垂线,与CB的延长线交于点E,根据A,B两点的纵坐标分别为1,2,可得出纵坐标,即可求得AE,BE,再根据勾股定理得出答案.
【详解】
解:过点A作x轴的垂线,与CB的延长线交于点E,
∵A,B两点在反比例函数的图象上且横坐标分别为1,2,
∴A,B纵坐标分别为2,1,
∴AE=1,BE=1,
∴AB= = .
故选B.
【点睛】
本题考查菱形的性质以及反比例函数图象上点的坐标特征,熟练掌握菱形的性质以及反比例函数图象上点的坐标特征是解题的关键.
3.C
【来源】江苏省苏州市高新区2020~2021学年下学期八年级数学期末试卷
【分析】
利用待定系数法求反比例函数解析式后将x=16代入函数解析式求出y的值即可.
【详解】
解:∵点B(12,18)在双曲线上,
∴,
解得:k=216.
当x=16时,y==13.5,
所以当x=16时,大棚内的温度约为13.5℃.
故选:C.
【点睛】
此题主要考查了反比例函数的应用,求出反比例函数解析式是解题关键.
4.C
【来源】四川省自贡市2021年中考数学真题
【分析】
将将代入求出U的值,即可判断A,B,D,利用反比例函数的增减性可判断C.
【详解】
解:设,将代入可得,故A错误;
∴蓄电池的电压是36V,故B错误;
当时,,该项正确;
当当时,,故D错误,
故选:C.
【点睛】
本题考查反比例函数的实际应用,掌握反比例函数的图象与性质是解题的关键.
5.B
【来源】2021年福建厦门同安区初中数学中考三模试题
【分析】
根据左视面向下放在地上,地面所受压强为,求出地面受到物体的压力,然后再根据“正视面向下放置地面时与左视面向下放置地面时,地面受到的压力不变”即可求解.
【详解】
解:由题意可知,设长方体的长、宽、高分别为4、2、1个单位长度,
则左视面的面积为4×1=4个平方单位,正视面的面积为4×2=8个平方单位,
由物理学公式:“压力=压强×受力面积”可知:
地面受到物体的压力,
正视面向下放置地面时与左视面向下放置地面时,地面受到的压力不变,
∴正视面向下放在地上时,地面受到的压强为:,
故选:B.
【点睛】
本题考查了数学知识的实际应用,理解压强与受力面积的关系本质是反比例函数的关系是解决本题的关键.
6.C
【来源】甘肃省酒泉市肃州区第六片区2019-2020学年九年级上学期期末数学试题
【详解】
试题解析:根据图象可得当时,
x的取值范围是:x< 6或0故选C.
7.C
【来源】北师大版九年级上册 第六章 6.3 反比例函数的应用
【分析】
先根据题意确定反比例关系式,再结合自变量的取值范围确定图象即可.
【详解】
根据题意可知,d与t之间的函数关系是反比例关系,即d=
且t>0.
故选:C.
【点睛】
本题主要考查了反比例函数的应用,以及根据实际意义画图和函数图象的读图能力.
8.B
【来源】山东省青岛市莱西市2020-2021学年八年级下学期期末数学试题
【分析】
由图可知为定值,即,易求出解析式,利用压强不超过,即时,求相对应的自变量的范围.
【详解】
解:设,
把代入,得,
,
.
由题意知,
,
即木板面积至少要有,
即不小于,
故选:B.
【点睛】
本题主要考查反比例函数在实际生活中的应用,解题的关键是正确得出函数关系式.
9.B
【来源】2020年湖北省武汉市中考数学训练试题(四)
【分析】
根据题意画出图形,结合图形列出y与x的函数关系式,再结合函数图象的性质解题即可.
【详解】
根据题意画图如下,
S△ECD=EC DF=
S△ECD=S矩形ABCD﹣S△AED﹣S△BCE
=6×8﹣×6×AE﹣
=48﹣
=48﹣3AB
=48﹣3×8
=24
∴,
y=(6≤x≤8)
可得出y与x的函数图象是一支在第一象限的双曲线.
故选:B.
【点睛】
本题主要考查反比函数的图象及应用,根据题意列出y与x的解析式是关键,同时也要注意到在实际问题中自变量的取值范围要考虑周全.当然,不同函数解析式所对应的函数图象是什么样子也要牢记.
10.反
【来源】2021年河北省唐山市路南区初中毕业升学数学三模试题
【分析】
设矩形的长为y,宽为x,根据矩形的面积为2,列式表示出矩形相邻两边的长的关系式并判断即可.
【详解】
解:设矩形的长为y,宽为x.
∵矩形的面积为2,
∴xy=2.
整理可得.
∴矩形相邻两边的长成反比例.
故答案为:反.
【点睛】
本题考查反比例函数的应用,列出题目中量之间的关系式是解题关键.
11.
【来源】江苏省东台市2018-2019学年八年级下学期期末数学试题
【解析】
【分析】
根据实际意义,写出函数的解析式即可.
【详解】
解:根据题意有:;
故与之间的函数图解析式为,
故答案为:.
【点睛】
本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限.
12. 25
【来源】湖北省十堰市丹江口市2020-2021学年九年级上学期期末数学试题
【分析】
(1)根据题意,可以写出v关于t的函数表达式;
(2)将代入(1)中的函数解析式即可解答本题.
【详解】
解:(1)由题意可得,
v关于t的函数表达式:,
故答案为:;
(2)由题意可得:
当时,,
∴平均每天要卸载25吨.
故答案为:25.
【点睛】
本题考查反比例函数的应用,解答本题的关键是明确题意,利用反比例函数的性质解答.
13.y=
【来源】人教版九年级 26.3 实际问题与反比例函数
【分析】
设该反比例函数的解析式为,然后将x=,y=400代入即可求出函数关系式.
【详解】
解:设该反比例函数的解析式为
将x=,y=400代入,得
解得:k=100
∴眼镜度数与镜片焦距之间的函数关系式为
故答案为:.
【点睛】
此题考查的是反比例函数的应用,掌握利用待定系数法求反比例函数解析式是解决此题的关键.
14.4
【来源】江苏省泰兴市济川中学2018-2019学年八年级下学期期中数学试题
【详解】
∵点A在曲线y=(x>0)上,AB⊥x轴,AB=1,
∴AB×OB=3,
∴OB=3,
∵CD垂直平分AO,
∴OC=AC,
∴△ABC的周长=AB+BC+AC=1+BC+OC=1+OB=1+3=4,
故答案为4.
【点睛】
运用了线段垂直平分线的性质以及反比例函数的性质.解题时注意运用线段垂直平分线上任意一点,到线段两端点的距离相等.
15.
【来源】山东省临沂市河东区2019-2020学年九年级上学期期末数学试题
【分析】
作AE⊥x轴于E,BF⊥x轴于F,过B点作BC⊥y轴于C,交AE于G,则 AG⊥BC,先求得△AOE≌△BAG,得出 AG=OE=n,BG=AE=1,从而求得 B(n+1, 1﹣n),根据 k=n×1=(n+1)(1﹣n)得出方程,解方程即可.
【详解】
作AE⊥x轴于E,BF⊥x轴于F,过B点作BC⊥y轴于C,交AE于G,
如图所示:则AG⊥BC,
∵∠OAB=90°,
∴∠OAE+∠BAG=90°,
∵∠OAE+∠AOE=90°,
∴∠AOE=∠GAB,
在△AOE和△BAG中,,
∴△AOE≌△BAG(AAS),
∴OE=AG,AE=BG,
∵点A(n,1),
∴AG=OE=n,BG=AE=1,
∴B(n+1,1﹣n),
∴k=n×1=(n+1)(1﹣n),整理得:n2+n﹣1=0,
解得:n= (负值舍去),
∴n= ,
∴k=;
故答案为.
【点睛】
本题考查了全等三角形的判定与性质、反比例函数图象上点的坐标特征、解方程等知识;熟练掌握反比例函数图象上点的坐标特征,证明三角形全等是解决问题的关键.
16.(2,0), (2,0).
【来源】山东省济宁市泗水县2020-2021学年九年级上学期期末数学试题
【分析】
根据等边三角形的性质以及反比例函数图象上点的坐标特征分别求出B2、B3、B4的坐标,得出规律,进而求出点Bn的坐标.
【详解】
解:如图,作A2C⊥x轴于点C,设B1C=a,则A2C=a,
OC=OB1+B1C=2+a,A2(2+a,a).
∵点A2在双曲线上,
∴(2+a) a=,
解得a=-1,或a=--1(舍去),
∴OB2=OB1+2B1C=2+2-2=2,
∴点B2的坐标为(2,0);
作A3D⊥x轴于点D,设B2D=b,则A3D=b,
OD=OB2+B2D=2+b,A2(2+b,b).
∵点A3在双曲线y=(x>0)上,
∴(2+b) b=,
解得b=-+,或b=--(舍去),
∴OB3=OB2+2B2D=2-2+2=2,
∴点B3的坐标为(2,0);
同理可得点B4的坐标为(2,0)即(4,0);
以此类推…,
∴点Bn的坐标为(2,0),
故答案为(2,0),(2,0).
【点睛】
本题考查了反比例函数图象上点的坐标特征,等边三角形的性质,正确求出B2、B3、B4的坐标进而得出点Bn的规律是解题的关键.
17. .
【来源】广东省深圳市高级中学2019-2020学年九年级上学期期中数学试题
【分析】
根据等边三角形的性质和已知条件,可求出,通过做垂线,利用解直角三角形,求出点的坐标,进而确定反比例函数的关系式;点在双曲线上,而它的纵横坐标都不知道,因此可以用直线的关系式与反比例函数的关系式组成方程组,解出的值,再进行取舍即可.
【详解】
过点、分别作,垂足为,
是等边三角形,
又,
,
在中,
,
;
反比例函数的关系式为:
在中,
,
,
设直线的关系式为,把代入得:
,解得:,
;
由题意得:,解得:,
,
,
故点的横坐标为:
【点睛】
考查等边三角形的性质、待定系数法求函数的表达式、以及将两个函数的关系式组成方程组,通过解方程组求出交点坐标,在此仅求交点的横坐标即可,也就是求出方程组中的的值.
18.(1)(t≥6);(2)蔬菜运输汽车早上8:00从巴东出发,不能在中午1:00到达武汉市场;(3)≤u≤.
【来源】湖北省恩施土家族苗族自治州巴东县2020-2021学年九年级下学期期中数学试题
【分析】
(1)根据表格中数据,可知v是t的反比例函数,设,然后利用待定系数法求出k即可;
(2)根据时间t=5,求出速度即可判断;
(3)根据自变量的取值范围,求出函数值的取值范围即可.
【详解】
解:(1)根据表格中数据,可知u是t的反比例函数,设,
∵当u=50时,t=12,
∴k=50×12=600,
∵u<100
∴t≥6
∴平均速度u关于行驶时间t的函数关系式(t≥6);
(2)∵从早上8:00到中午1:00共5小时
∴t=5时,=120> 100
∴蔬菜运输汽车早上8:00从巴东出发,不能在中午1:00到达武汉市场;
(3)∵7≤t≤9.5,
∴≤u≤,即≤u≤.
答:平均速度的取值范围是≤u≤.
【点睛】
本题考查反比例函数的应用、待定系数法等知识点,理解题意、求得函数解析式是解答本题的关键.
19.(1)y=2x,0≤x≤4,;(2)20;(3)此次消毒有效,理由见解析
【来源】福建省泉州市2020-2021学年八年级下学期期中数学试题
【分析】
(1)当0≤x≤4时,药物燃烧时y与x之间是正比例函数关系,根据(4,8)利用待定系数法即可求出y与x之间的函数关系式;当x>8时,药物燃烧后y与x的函数关系是反比例函数关系,根据(4,8)利用待定系数法即可求出y与x之间的函数关系式;
(2)将y=1.6代入反比例函数关系式,就可求出对应的自变量的值,结合函数图像解答即可;
(3)把y=2代入正比例函数解析式和反比例函数解析式,求出相应的x,它们之差与14进行比较,若大于等于14就有效.
【详解】
解:(1) 当0≤x≤4时,设y=kx,把(4,8)代入得8=4k,即k=2
∴y= 2x(0≤x≤4);
当x>4时,设y=,把(4,8)代入得8=,即m=32
∴y= (x>4)
故填y=2x,0≤x≤4,;
(2)当y=1.6时,则有=1.6,解答x=20
结合图像知,至少需要经过20分钟后,学生才能回到教室;
(3)此次消毒有效,理由如下:
把y=2代入y= 2 x,得:x=1
把y=2代入y= ,得:x=16
∵16﹣1=15>14.
∴这次消毒是有效的.
【点睛】
本题主要考查了正比例函数和反比例函数的应用、运用待定系数法求函数解析式,审清题意、明确量之间的关系是解答本题的关键.
20.(1);(2)180台,30台
【来源】【北师大版课时练习】九年级数学上册第五章 反比例函数 3 反比例函数的应用
【分析】
(1)首先根据题意,因总工作量为9000台空调,故每天组装的台数与生产时间之间成反比例关系,即;
(2)计算出当时,;当时,;比较即可得答案.
【详解】
解:(1)每天组装的台数(单位:台天)与生产时间(单位:天)之间的函数关系:;
(2)当时,.
所以,这批空调提前10天上市,那么原装配车间每天至少要组装180台空调,
原计划用2个月时间(每月按30天计算)完成这一任务,则每天组装150台,
即比原计划多:台.
【点睛】
本题考查反比例函数的解析式、性质与运用,解题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式,进一步根据题意求解答案.
21.(1)y=;(2)小华选择方案二购买,见解析.
【来源】福建省福州市鼓楼区福州屏东中学2020-2021学年九年级下学期4月月考数学试题
【分析】
(1)设每件商品实付款的均价为元,购买商品A的件数为x件,根据x的条件得出y得值即可;
(2)x=5,分类讨论即可;
【详解】
解:(1)设每件商品实付款的均价为y元,购买商品A的件数为x件,
当0<x≤4时,y=59,
当4<x≤8时,y=,
综上,y=;
(2)方案一:x=5,y=59﹣,
方案二:x=5(买5件退一件),
y=
∴小华选择方案二购买.
【点睛】
本题主要考查了反比例函数的应用,准确分析计算是解题的关键.
22.任务1:(1)补全表格;416.0,415.0;(2)见解析;(3)6;任务2:需要考虑这一优惠条件,理由见解析.
【来源】2021年山西省太原市中考数学一模试题
【分析】
(1)根据题意列出x与y的函数关系,再求出和对应的y值,再补充表格即可;
(2)根据表格信息一一对应描点即可;
(3)根据图中得出信息,求出10天购买一次饲料享受优惠的费用,再和原来10天购买一次饲料的费用比较得出结论.
【详解】
任务1:
(1)设每天购买一次饲料,平均每天支付的总费用为元,
饲料的保管费与其他费用每天比前一天少(元).
∴ 天饲料的保管费用共:
=
=
=
∴
∴当时,
当时,
补全表格;
x/天 … 2 3 4 5 6 7 8 9 10 …
Y/元 … 455.0 430.0 420.0 416.0 415.0 415.7 417.5 420.0 423.0 …
(2)如图所示;
(3)由图可知,养殖场6天购买一次饲养才能使平均每天支付的总费用最少,
若考虑此优惠条件,则10天购买一次饲料,
当时,,享受优惠后90%=380.7(元),
由(2)可知,不享受优惠时,最小为415,
∵,∴需要享受这一优惠条件.
【点睛】
本题考查了函数与实际问题的应用,理解题意,学会运用函数与方程的思想是解题的关键.答案第16页,共16页
答案第15页,共16页
26.2 实际问题与反比例函数 专题练习
一、选择题:
1.甲、乙两地相距100千米,某人开车从甲地到乙地,那么它的速度v(千米/小时)与时间t(小时)之间的函数关系用图象表示大致为( )
A. B. C. D.
2.如图,在平面直角坐示系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的横坐标分别为1,2,反比例函数的图像经过A,B两点,则菱形ABCD的边长为()
A.1 B. C.2 D.
3.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种蔬菜.上图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图像,其中BC段是双曲线(k≠0)的一部分,则当x = 16时,大棚内的温度约为( )
A.18℃ B.15.5℃ C.13.5℃ D.12℃
4.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为 B.蓄电池的电压是18V
C.当时, D.当时,
5.如图,一块长方体砖块的长、宽、高的比为,如果左视面向下放在地上,地面所受压强为,则正视面向下放在地上时,地面所受压强为( )
A. B. C. D.
6.如图,直线与双曲线交于、两点,则当时,x的取值范围是
A.或
B.或
C.或
D.
7.已知某种品牌电脑的显示器的使用寿命大约为时,这种显示器工作的天数为d(天),平均每天工作的时间为t(时),那么d与t之间的函数图象大致是( )
A. B. C. D.
8.某校科技小组进行野外考察,途中遇到一片十几米宽的湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺若干块木板,构筑成一条临时通道,木板对地面的压强风是木板面积的反比例函数,其图象如图所示,当木板压强不超过时,木板的面积应为( )
A.不大于 B.不小于 C.不大于 D.不小于
9.在矩形ABCD中,E点为AB上的一点,AB=8,AD=6,连接CE,作DF⊥CE于F点,令CE=x,DF=y,下列关于y与x的函数关系图象大致是( )
A. B.
C. D.
二、填空题:
10.若矩形的面积为2,则矩形相邻两边的长成______比例.
11.甲、乙两地相距200千米,汽车从甲地匀速行驶到乙地,汽车行驶时间关于行驶速度的函数表达式是_____.
12.码头工人每天往一艘轮船上装载20吨货物,装载完毕恰好用了10天时间.轮船到达目的地后开始卸货,记平均卸货速度为v(单位:吨/天),卸货天数为t.则v关于t的函数表达式为________;如果船上的货物8天卸载完毕,那么平均每天要卸载________吨货物.
13.近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25m,则眼镜度数与镜片焦距之间的函数关系式为________.
14.如图,点A在曲线y=(x>0)上,过点A作AB⊥x轴,垂足为B,OA的垂直平分线交OB、OA于点C、D,当AB=1时,△ABC的周长为_____.
15.如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y=(x>0)的图象经过A,B两点.若点A的坐标为(n,1),则 k的值为______.
16.如图,已知等边,顶点在双曲线上,点的坐标为(2,0).过作,交双曲线于点,过作交轴于,得到第二个等边.过作交双曲线于点,过作交轴于点得到第三个等边;以此类推,…,则点的坐标为______,的坐标为______.
17.如图,在平面直角坐标系中,函数的图象与等边三角形的边,分别交于点,,且,若,那么点的横坐标为___________.
三、解答题:
18.巴东某公司将绿葱坡无公害蔬菜运往武汉市场销售.记汽车行驶的时间为t小时,平均速度为u千米/小时(汽车行驶速度不能超过100千米/小时),司机根据经验,提供如下表所列一组t,u的对应值:
u(千米/小时) 50 75 80 90 95
t(小时) 12 8 7.5 6.67 6.32
(1)根据表中的数据,请你求出平均速度u关于行驶时间t的函数关系式;
(2)若蔬菜运输汽车早上8:00从巴东出发,能否在中午1:00到达武汉市场?请说明理由;
(3)长途开车要杜绝疲劳驾驶,但又要减小蔬菜长途运输的损耗. 因此,汽车到达武汉市场的行驶时间t满足7≤t≤9.5为佳,求平均速度u的取值范围.
19.根据传染病防控制度的要求,学校必须对教室定期用药熏消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物燃烧完毕后,y(毫克)与时间x(分钟)成反比例,如图所示.请根据图中所提供的信息,解答下列问题:
(1)当药物燃烧时,y关于x的函数关系式为 ,自变量x的取值范围为 ;药物燃烧后,y关于x的函数关系式为 ;
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进入教室,则从消毒开始,至少需要经过 分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于2毫克且持续时间不低于14分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
20.某空调生产厂的装配车间计划在一段时期内组装9000台空调.
(1)在这段时期内,每天组装的数量m(台/天)与组装的时间t(天)之间有怎样的函数关系?
(2)原计划用2个月时间(每月按30天计算)完成这一任务,但由于气温提前升高,厂家决定这批空调提前10天完成组装,那么装配车间每天至少要组装多少台空调?比原计划多多少?
21.某电商店铺为促销一件标价59元的商品A,制定了以下促销方案:在指定日期购买商品A(限购8件),除包邮外,享受每满240元(标价)减40元,但在收货之前不能退换,小华正好需要该商品,于是计划等到优惠日期进行购买.
(1)请求出小华每件商品实付款的均价与购买商品A的件数的关系;
(2)小华对该商品的实际需求为4件,为了追求最大优惠,小华考虑以下两种方案:
方案一:直接按店铺优惠活动进行购买,不退货;
方案二:凑单享受满减,即购买恰好享受下一级满减活动的件数,然后将超过自己需要的部分商品以实付款均价退回,但需要自行承担退货的运费(运费规则:首件10元,每多一件加4元).
若以小华的实际支出均价(实际支出均价=)为依据,请你为小华选择一个优惠的购买方案.
22.某养殖场需要定期购买饲料,已知该养殖场每天需要200千克饲料,饲料的价格为1.8元/千克,饲料的保管费与其他费用平均每天为0.05元/千克,购买饲料每次的运费为180元.
任务1:该养殖场多少天购买一次饲料才能使平均每天支付的总费用最少;
小明的分析如下:如果2天购买一次,则保管费与其他费用需支付200×0.05=10(元);如果3天购买一次,则保管费与其他费用需支付200×2×0.05+200×0.05=30(元);如果4天购买一次,则保管费与其他费用需支付200×3×0.05+200×2×0.05+200×0.05=60(元),他发现已有的数学模型不能解决这个问题,想到了用函数图象的方法解决,设x天购买一次饲料,平均每天支付的总费用为y元,下面是他解决这个问题的过程,请解答相关问题.
(1)计算得到x与y的部分对应值如下表,请补全表格;
x/天 … 2 3 4 5 6 7 8 9 10 …
Y/元 … 455.0 430.0 420.0 415.7 417.5 420.0 423.0 …
(2)在平面直角坐标系中,描出(1)中所对应的点;
(3)结合图象:养殖场 天购买一次饲料才能使平均每天支付的总费用最少.
任务2:提供饲料的公司规定,当一次购买饲料不少于2000千克时,价格可享受九折优惠,在该养殖场购买饲料时是否需要考虑这一优惠条件,简要说明理由.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.D
【来源】考点12 反比例函数—2021年《三步冲刺中考 数学》(广东专版)之第1步小题夯基础
【分析】
直接利用速度= ,进而得出函数关系式,即可得出其函数图形.
【详解】
解:∵甲、乙两地相距100千米,某人开车从甲地到乙地,
∴它的速度v(千米/小时)与时间t(小时)之间的函数关系为:v= (t>0),
则此函数关系用图象表示大致为:
.
故选:D.
【点睛】
此题考查反比例函数的实际应用,难度一般.
2.B
【来源】【万唯原创】2020年山西-面对面-选填题组5
【分析】
过点A作x轴的垂线,与CB的延长线交于点E,根据A,B两点的纵坐标分别为1,2,可得出纵坐标,即可求得AE,BE,再根据勾股定理得出答案.
【详解】
解:过点A作x轴的垂线,与CB的延长线交于点E,
∵A,B两点在反比例函数的图象上且横坐标分别为1,2,
∴A,B纵坐标分别为2,1,
∴AE=1,BE=1,
∴AB= = .
故选B.
【点睛】
本题考查菱形的性质以及反比例函数图象上点的坐标特征,熟练掌握菱形的性质以及反比例函数图象上点的坐标特征是解题的关键.
3.C
【来源】江苏省苏州市高新区2020~2021学年下学期八年级数学期末试卷
【分析】
利用待定系数法求反比例函数解析式后将x=16代入函数解析式求出y的值即可.
【详解】
解:∵点B(12,18)在双曲线上,
∴,
解得:k=216.
当x=16时,y==13.5,
所以当x=16时,大棚内的温度约为13.5℃.
故选:C.
【点睛】
此题主要考查了反比例函数的应用,求出反比例函数解析式是解题关键.
4.C
【来源】四川省自贡市2021年中考数学真题
【分析】
将将代入求出U的值,即可判断A,B,D,利用反比例函数的增减性可判断C.
【详解】
解:设,将代入可得,故A错误;
∴蓄电池的电压是36V,故B错误;
当时,,该项正确;
当当时,,故D错误,
故选:C.
【点睛】
本题考查反比例函数的实际应用,掌握反比例函数的图象与性质是解题的关键.
5.B
【来源】2021年福建厦门同安区初中数学中考三模试题
【分析】
根据左视面向下放在地上,地面所受压强为,求出地面受到物体的压力,然后再根据“正视面向下放置地面时与左视面向下放置地面时,地面受到的压力不变”即可求解.
【详解】
解:由题意可知,设长方体的长、宽、高分别为4、2、1个单位长度,
则左视面的面积为4×1=4个平方单位,正视面的面积为4×2=8个平方单位,
由物理学公式:“压力=压强×受力面积”可知:
地面受到物体的压力,
正视面向下放置地面时与左视面向下放置地面时,地面受到的压力不变,
∴正视面向下放在地上时,地面受到的压强为:,
故选:B.
【点睛】
本题考查了数学知识的实际应用,理解压强与受力面积的关系本质是反比例函数的关系是解决本题的关键.
6.C
【来源】甘肃省酒泉市肃州区第六片区2019-2020学年九年级上学期期末数学试题
【详解】
试题解析:根据图象可得当时,
x的取值范围是:x< 6或0
7.C
【来源】北师大版九年级上册 第六章 6.3 反比例函数的应用
【分析】
先根据题意确定反比例关系式,再结合自变量的取值范围确定图象即可.
【详解】
根据题意可知,d与t之间的函数关系是反比例关系,即d=
且t>0.
故选:C.
【点睛】
本题主要考查了反比例函数的应用,以及根据实际意义画图和函数图象的读图能力.
8.B
【来源】山东省青岛市莱西市2020-2021学年八年级下学期期末数学试题
【分析】
由图可知为定值,即,易求出解析式,利用压强不超过,即时,求相对应的自变量的范围.
【详解】
解:设,
把代入,得,
,
.
由题意知,
,
即木板面积至少要有,
即不小于,
故选:B.
【点睛】
本题主要考查反比例函数在实际生活中的应用,解题的关键是正确得出函数关系式.
9.B
【来源】2020年湖北省武汉市中考数学训练试题(四)
【分析】
根据题意画出图形,结合图形列出y与x的函数关系式,再结合函数图象的性质解题即可.
【详解】
根据题意画图如下,
S△ECD=EC DF=
S△ECD=S矩形ABCD﹣S△AED﹣S△BCE
=6×8﹣×6×AE﹣
=48﹣
=48﹣3AB
=48﹣3×8
=24
∴,
y=(6≤x≤8)
可得出y与x的函数图象是一支在第一象限的双曲线.
故选:B.
【点睛】
本题主要考查反比函数的图象及应用,根据题意列出y与x的解析式是关键,同时也要注意到在实际问题中自变量的取值范围要考虑周全.当然,不同函数解析式所对应的函数图象是什么样子也要牢记.
10.反
【来源】2021年河北省唐山市路南区初中毕业升学数学三模试题
【分析】
设矩形的长为y,宽为x,根据矩形的面积为2,列式表示出矩形相邻两边的长的关系式并判断即可.
【详解】
解:设矩形的长为y,宽为x.
∵矩形的面积为2,
∴xy=2.
整理可得.
∴矩形相邻两边的长成反比例.
故答案为:反.
【点睛】
本题考查反比例函数的应用,列出题目中量之间的关系式是解题关键.
11.
【来源】江苏省东台市2018-2019学年八年级下学期期末数学试题
【解析】
【分析】
根据实际意义,写出函数的解析式即可.
【详解】
解:根据题意有:;
故与之间的函数图解析式为,
故答案为:.
【点睛】
本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限.
12. 25
【来源】湖北省十堰市丹江口市2020-2021学年九年级上学期期末数学试题
【分析】
(1)根据题意,可以写出v关于t的函数表达式;
(2)将代入(1)中的函数解析式即可解答本题.
【详解】
解:(1)由题意可得,
v关于t的函数表达式:,
故答案为:;
(2)由题意可得:
当时,,
∴平均每天要卸载25吨.
故答案为:25.
【点睛】
本题考查反比例函数的应用,解答本题的关键是明确题意,利用反比例函数的性质解答.
13.y=
【来源】人教版九年级 26.3 实际问题与反比例函数
【分析】
设该反比例函数的解析式为,然后将x=,y=400代入即可求出函数关系式.
【详解】
解:设该反比例函数的解析式为
将x=,y=400代入,得
解得:k=100
∴眼镜度数与镜片焦距之间的函数关系式为
故答案为:.
【点睛】
此题考查的是反比例函数的应用,掌握利用待定系数法求反比例函数解析式是解决此题的关键.
14.4
【来源】江苏省泰兴市济川中学2018-2019学年八年级下学期期中数学试题
【详解】
∵点A在曲线y=(x>0)上,AB⊥x轴,AB=1,
∴AB×OB=3,
∴OB=3,
∵CD垂直平分AO,
∴OC=AC,
∴△ABC的周长=AB+BC+AC=1+BC+OC=1+OB=1+3=4,
故答案为4.
【点睛】
运用了线段垂直平分线的性质以及反比例函数的性质.解题时注意运用线段垂直平分线上任意一点,到线段两端点的距离相等.
15.
【来源】山东省临沂市河东区2019-2020学年九年级上学期期末数学试题
【分析】
作AE⊥x轴于E,BF⊥x轴于F,过B点作BC⊥y轴于C,交AE于G,则 AG⊥BC,先求得△AOE≌△BAG,得出 AG=OE=n,BG=AE=1,从而求得 B(n+1, 1﹣n),根据 k=n×1=(n+1)(1﹣n)得出方程,解方程即可.
【详解】
作AE⊥x轴于E,BF⊥x轴于F,过B点作BC⊥y轴于C,交AE于G,
如图所示:则AG⊥BC,
∵∠OAB=90°,
∴∠OAE+∠BAG=90°,
∵∠OAE+∠AOE=90°,
∴∠AOE=∠GAB,
在△AOE和△BAG中,,
∴△AOE≌△BAG(AAS),
∴OE=AG,AE=BG,
∵点A(n,1),
∴AG=OE=n,BG=AE=1,
∴B(n+1,1﹣n),
∴k=n×1=(n+1)(1﹣n),整理得:n2+n﹣1=0,
解得:n= (负值舍去),
∴n= ,
∴k=;
故答案为.
【点睛】
本题考查了全等三角形的判定与性质、反比例函数图象上点的坐标特征、解方程等知识;熟练掌握反比例函数图象上点的坐标特征,证明三角形全等是解决问题的关键.
16.(2,0), (2,0).
【来源】山东省济宁市泗水县2020-2021学年九年级上学期期末数学试题
【分析】
根据等边三角形的性质以及反比例函数图象上点的坐标特征分别求出B2、B3、B4的坐标,得出规律,进而求出点Bn的坐标.
【详解】
解:如图,作A2C⊥x轴于点C,设B1C=a,则A2C=a,
OC=OB1+B1C=2+a,A2(2+a,a).
∵点A2在双曲线上,
∴(2+a) a=,
解得a=-1,或a=--1(舍去),
∴OB2=OB1+2B1C=2+2-2=2,
∴点B2的坐标为(2,0);
作A3D⊥x轴于点D,设B2D=b,则A3D=b,
OD=OB2+B2D=2+b,A2(2+b,b).
∵点A3在双曲线y=(x>0)上,
∴(2+b) b=,
解得b=-+,或b=--(舍去),
∴OB3=OB2+2B2D=2-2+2=2,
∴点B3的坐标为(2,0);
同理可得点B4的坐标为(2,0)即(4,0);
以此类推…,
∴点Bn的坐标为(2,0),
故答案为(2,0),(2,0).
【点睛】
本题考查了反比例函数图象上点的坐标特征,等边三角形的性质,正确求出B2、B3、B4的坐标进而得出点Bn的规律是解题的关键.
17. .
【来源】广东省深圳市高级中学2019-2020学年九年级上学期期中数学试题
【分析】
根据等边三角形的性质和已知条件,可求出,通过做垂线,利用解直角三角形,求出点的坐标,进而确定反比例函数的关系式;点在双曲线上,而它的纵横坐标都不知道,因此可以用直线的关系式与反比例函数的关系式组成方程组,解出的值,再进行取舍即可.
【详解】
过点、分别作,垂足为,
是等边三角形,
又,
,
在中,
,
;
反比例函数的关系式为:
在中,
,
,
设直线的关系式为,把代入得:
,解得:,
;
由题意得:,解得:,
,
,
故点的横坐标为:
【点睛】
考查等边三角形的性质、待定系数法求函数的表达式、以及将两个函数的关系式组成方程组,通过解方程组求出交点坐标,在此仅求交点的横坐标即可,也就是求出方程组中的的值.
18.(1)(t≥6);(2)蔬菜运输汽车早上8:00从巴东出发,不能在中午1:00到达武汉市场;(3)≤u≤.
【来源】湖北省恩施土家族苗族自治州巴东县2020-2021学年九年级下学期期中数学试题
【分析】
(1)根据表格中数据,可知v是t的反比例函数,设,然后利用待定系数法求出k即可;
(2)根据时间t=5,求出速度即可判断;
(3)根据自变量的取值范围,求出函数值的取值范围即可.
【详解】
解:(1)根据表格中数据,可知u是t的反比例函数,设,
∵当u=50时,t=12,
∴k=50×12=600,
∵u<100
∴t≥6
∴平均速度u关于行驶时间t的函数关系式(t≥6);
(2)∵从早上8:00到中午1:00共5小时
∴t=5时,=120> 100
∴蔬菜运输汽车早上8:00从巴东出发,不能在中午1:00到达武汉市场;
(3)∵7≤t≤9.5,
∴≤u≤,即≤u≤.
答:平均速度的取值范围是≤u≤.
【点睛】
本题考查反比例函数的应用、待定系数法等知识点,理解题意、求得函数解析式是解答本题的关键.
19.(1)y=2x,0≤x≤4,;(2)20;(3)此次消毒有效,理由见解析
【来源】福建省泉州市2020-2021学年八年级下学期期中数学试题
【分析】
(1)当0≤x≤4时,药物燃烧时y与x之间是正比例函数关系,根据(4,8)利用待定系数法即可求出y与x之间的函数关系式;当x>8时,药物燃烧后y与x的函数关系是反比例函数关系,根据(4,8)利用待定系数法即可求出y与x之间的函数关系式;
(2)将y=1.6代入反比例函数关系式,就可求出对应的自变量的值,结合函数图像解答即可;
(3)把y=2代入正比例函数解析式和反比例函数解析式,求出相应的x,它们之差与14进行比较,若大于等于14就有效.
【详解】
解:(1) 当0≤x≤4时,设y=kx,把(4,8)代入得8=4k,即k=2
∴y= 2x(0≤x≤4);
当x>4时,设y=,把(4,8)代入得8=,即m=32
∴y= (x>4)
故填y=2x,0≤x≤4,;
(2)当y=1.6时,则有=1.6,解答x=20
结合图像知,至少需要经过20分钟后,学生才能回到教室;
(3)此次消毒有效,理由如下:
把y=2代入y= 2 x,得:x=1
把y=2代入y= ,得:x=16
∵16﹣1=15>14.
∴这次消毒是有效的.
【点睛】
本题主要考查了正比例函数和反比例函数的应用、运用待定系数法求函数解析式,审清题意、明确量之间的关系是解答本题的关键.
20.(1);(2)180台,30台
【来源】【北师大版课时练习】九年级数学上册第五章 反比例函数 3 反比例函数的应用
【分析】
(1)首先根据题意,因总工作量为9000台空调,故每天组装的台数与生产时间之间成反比例关系,即;
(2)计算出当时,;当时,;比较即可得答案.
【详解】
解:(1)每天组装的台数(单位:台天)与生产时间(单位:天)之间的函数关系:;
(2)当时,.
所以,这批空调提前10天上市,那么原装配车间每天至少要组装180台空调,
原计划用2个月时间(每月按30天计算)完成这一任务,则每天组装150台,
即比原计划多:台.
【点睛】
本题考查反比例函数的解析式、性质与运用,解题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式,进一步根据题意求解答案.
21.(1)y=;(2)小华选择方案二购买,见解析.
【来源】福建省福州市鼓楼区福州屏东中学2020-2021学年九年级下学期4月月考数学试题
【分析】
(1)设每件商品实付款的均价为元,购买商品A的件数为x件,根据x的条件得出y得值即可;
(2)x=5,分类讨论即可;
【详解】
解:(1)设每件商品实付款的均价为y元,购买商品A的件数为x件,
当0<x≤4时,y=59,
当4<x≤8时,y=,
综上,y=;
(2)方案一:x=5,y=59﹣,
方案二:x=5(买5件退一件),
y=
∴小华选择方案二购买.
【点睛】
本题主要考查了反比例函数的应用,准确分析计算是解题的关键.
22.任务1:(1)补全表格;416.0,415.0;(2)见解析;(3)6;任务2:需要考虑这一优惠条件,理由见解析.
【来源】2021年山西省太原市中考数学一模试题
【分析】
(1)根据题意列出x与y的函数关系,再求出和对应的y值,再补充表格即可;
(2)根据表格信息一一对应描点即可;
(3)根据图中得出信息,求出10天购买一次饲料享受优惠的费用,再和原来10天购买一次饲料的费用比较得出结论.
【详解】
任务1:
(1)设每天购买一次饲料,平均每天支付的总费用为元,
饲料的保管费与其他费用每天比前一天少(元).
∴ 天饲料的保管费用共:
=
=
=
∴
∴当时,
当时,
补全表格;
x/天 … 2 3 4 5 6 7 8 9 10 …
Y/元 … 455.0 430.0 420.0 416.0 415.0 415.7 417.5 420.0 423.0 …
(2)如图所示;
(3)由图可知,养殖场6天购买一次饲养才能使平均每天支付的总费用最少,
若考虑此优惠条件,则10天购买一次饲料,
当时,,享受优惠后90%=380.7(元),
由(2)可知,不享受优惠时,最小为415,
∵,∴需要享受这一优惠条件.
【点睛】
本题考查了函数与实际问题的应用,理解题意,学会运用函数与方程的思想是解题的关键.答案第16页,共16页
答案第15页,共16页
