2021-2022学年北师大版九年级数学上册6.3 反比例函数的应用同步测试卷(Word版,附答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册6.3 反比例函数的应用同步测试卷(Word版,附答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 220.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-21 23:55:48 | ||
图片预览




文档简介
6.3 反比例函数的应用同步测试卷 2021-2022学年北师大版九年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共8小题,共40分)
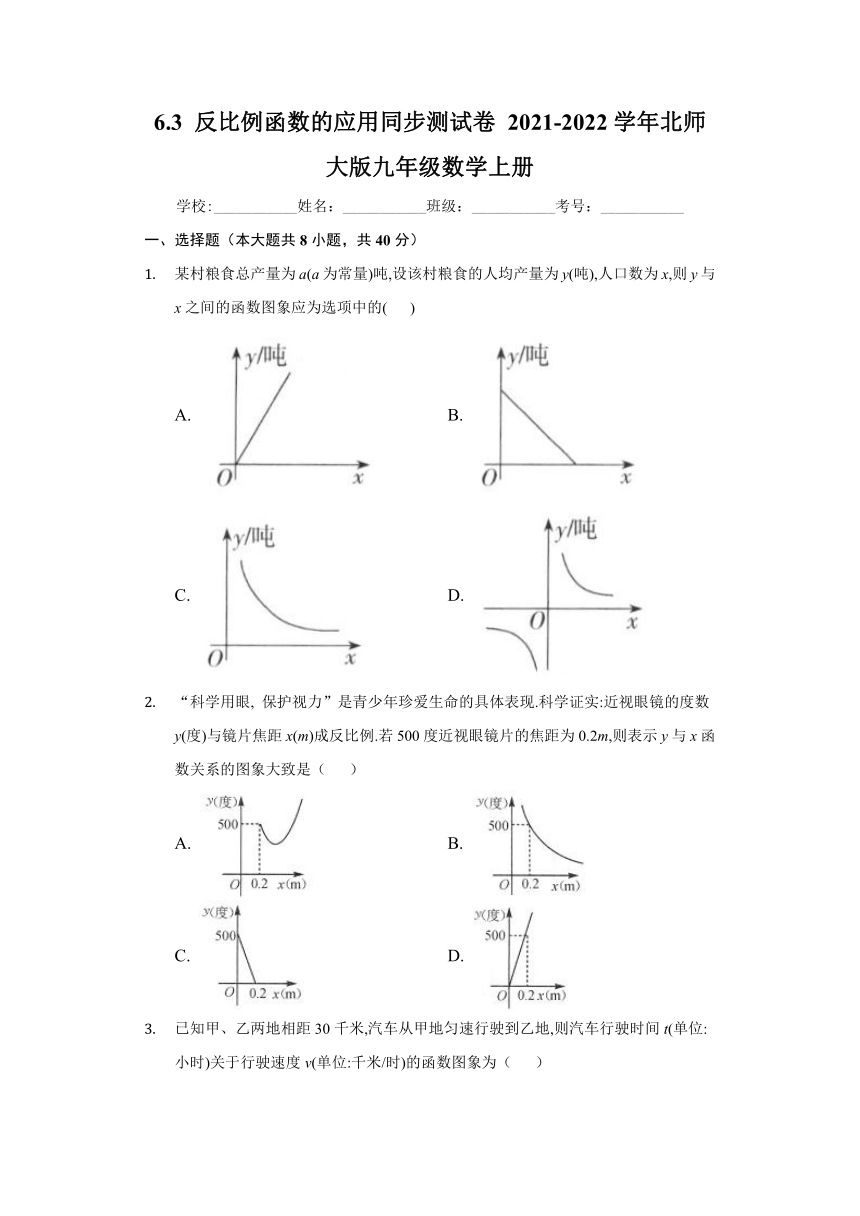
某村粮食总产量为a(a为常量)吨,设该村粮食的人均产量为y(吨),人口数为x,则y与x之间的函数图象应为选项中的( )
A. B.
C. D.
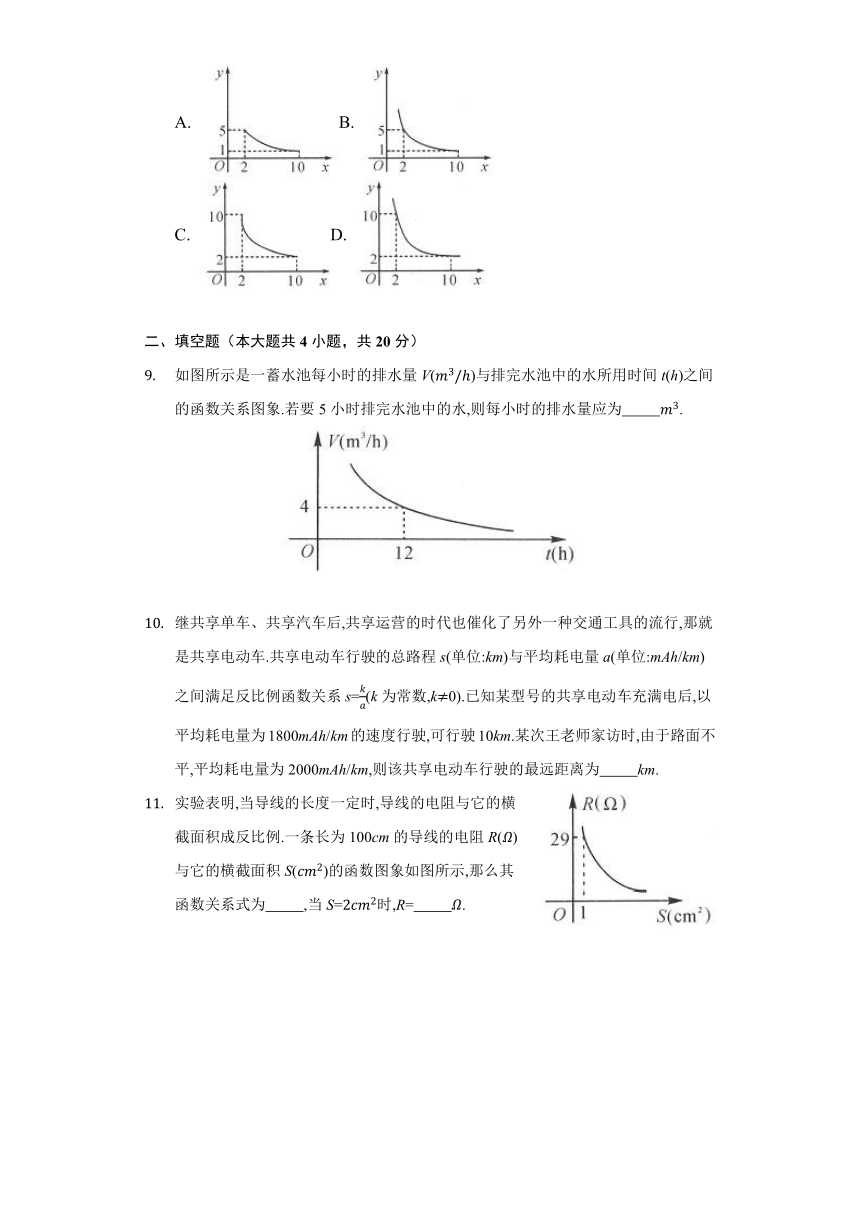
“科学用眼, 保护视力”是青少年珍爱生命的具体表现.科学证实:近视眼镜的度数y(度)与镜片焦距x(m)成反比例.若500度近视眼镜片的焦距为0.2m,则表示y与x函数关系的图象大致是( )
A. B.
C. D.
已知甲、乙两地相距30千米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/时)的函数图象为( )
A. B.
C. D.
一辆汽车的前灯电路上的电压(U)保持不变,通过前灯的电流强度(I)越大,灯就越亮,且I=(R:前灯电阻).已知A、B两种前灯灯泡的电阻分别为、,若发现使用灯泡A时,汽车前灯的灯光更亮,则正确的是( )
A. B.
C. D. 与,大小无关
反比例函数y=与一次函数y=x+的图象有一个交点B(,m),则k的值为( )
A. B. C. D.
公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”:阻力阻力臂=动力动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1500N和0.4m,则动力F (单位:N)关于动力臂L(单位:m)的函数表达式正确的是( )
A. B. C. D.
公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力阻力臂=动力动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200N和0.5m,则动力F(单位:N)关于动力臂l(单位:m)的函数表达式正确的是( )
A. B. C. D.
一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图所示,设小矩形的长和宽分别为x,y,剪去部分面积为20.若2x10,则y与x的函数图象是( )
A. B.
C. D.
二、填空题(本大题共4小题,共20分)
如图所示是一蓄水池每小时的排水量V()与排完水池中的水所用时间t(h)之间的函数关系图象.若要5小时排完水池中的水,则每小时的排水量应为 .
继共享单车、共享汽车后,共享运营的时代也催化了另外一种交通工具的流行,那就是共享电动车.共享电动车行驶的总路程s(单位:km)与平均耗电量a(单位:mAh/km)之间满足反比例函数关系s=(k为常数,k0).已知某型号的共享电动车充满电后,以平均耗电量为1800mAh/km的速度行驶,可行驶10km.某次王老师家访时,由于路面不平,平均耗电量为2000mAh/km,则该共享电动车行驶的最远距离为 km.
实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例.一条长为100cm的导线的电阻R()与它的横截面积S()的函数图象如图所示,那么其函数关系式为 ,当S=时,R= .
如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作(m为1~8的整数).函数y=(x<0)的图象为曲线L.
(1)若L过点,则k= ;(2)若L过点,则它必定还过另一点,则m= ;
(3)若曲线L使得~这些点分布在它的两侧,每侧各4个点,则k的整数值有 个.
三、解答题(本大题共3小题,共40分)
在平面直角坐标系xOy中,反比例函数y=(x>0)的图象经过点A(3,4),过点A的直线y=kx+b与x轴、y轴分别交于B,C两点.
(1)求反比例函数的表达式;
(2)若AOB的面积为BOC的面积的2倍,求此直线的函数表达式.
在滑草过程中,小明发现滑道两边形如两条双曲线,如图,点,,,在反比例函数y=(x>0)的图象上,点,,,在反比例函数y=(k>1,x>0)的图象上,y轴,已知点,,的横坐标分别为1,2,,令四边形、的面积分别为、、.
(1)用含k的代数式表示= ;
(2)若=39,则k= .
为了探索函数y=x+(x>0)的图象与性质,我们参照学习函数的过程与方法.列表:
x ... 1 2 3 4 5 ...
y
... 2 ...
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图a所示:
(1)如图a,观察所描出点的分布,用一条光滑曲线将点顺次连接起来,画出函数图象;
(2)已知点(,),(,)在函数图象上,结合表格和函数图象,回答下列问题:
若0<<1,则 ;若1<<,则 ;若=1,则 (填“>”“=”或“<”);
(3)某农户要建造一个如图b所示的长方体无盖水池,其底面积为1平方米,深为1米.已知底面造价为1千元/平方米,侧面造价为0.5千元/平方米.设水池底面一边的长为x米,水池总造价为y千元.
请写出y与x之间的函数关系式;
若该农户预算不超过3.5千元,则水池底面一边的长x应控制在什么范围内
1.【答案】C
2.【答案】B
3.【答案】D
4.【答案】C
5.【答案】C
6.【答案】C
7.【答案】B
8.【答案】A
9.【答案】9.6
10.【答案】9
11.【答案】R=
14.5
12.【答案】-16
5
7
13.【答案】解:(1)反比例函数y=(x>0)的图象经过点A(3,4),
m=34=12,
反比例函数的表达式为y=.
(2)直线y=kx+b过点A,
3k+b=4.
过点A的直线y=kx+b与x轴、y轴分别交于B,C两点,
B(-,0),C(0,b).
AOB的面积为BOC的面积的2倍,
4=2,
b=2,
当b=2时,k=,
当b=-2时,k=2,
此直线的函数表达式为y=x+2或y=2x-2.
14.【答案】(1)(k-1);
(2)761.
15.【答案】解:(1)画函数图象如图所示:
(2)若0<<1,则>;若1<<,则<;若=1,则 =.
故答案为>;<;=.
(3)由题意,得y=1+(2x+)0.5=1+x+(x>0).
观察图象可得,当x2时,x+2.5,即y=1+x+3.5,
答:水池底面一边的长x应控制在x2的范围内.
第2页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共8小题,共40分)
某村粮食总产量为a(a为常量)吨,设该村粮食的人均产量为y(吨),人口数为x,则y与x之间的函数图象应为选项中的( )
A. B.
C. D.
“科学用眼, 保护视力”是青少年珍爱生命的具体表现.科学证实:近视眼镜的度数y(度)与镜片焦距x(m)成反比例.若500度近视眼镜片的焦距为0.2m,则表示y与x函数关系的图象大致是( )
A. B.
C. D.
已知甲、乙两地相距30千米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/时)的函数图象为( )
A. B.
C. D.
一辆汽车的前灯电路上的电压(U)保持不变,通过前灯的电流强度(I)越大,灯就越亮,且I=(R:前灯电阻).已知A、B两种前灯灯泡的电阻分别为、,若发现使用灯泡A时,汽车前灯的灯光更亮,则正确的是( )
A. B.
C. D. 与,大小无关
反比例函数y=与一次函数y=x+的图象有一个交点B(,m),则k的值为( )
A. B. C. D.
公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”:阻力阻力臂=动力动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1500N和0.4m,则动力F (单位:N)关于动力臂L(单位:m)的函数表达式正确的是( )
A. B. C. D.
公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力阻力臂=动力动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200N和0.5m,则动力F(单位:N)关于动力臂l(单位:m)的函数表达式正确的是( )
A. B. C. D.
一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图所示,设小矩形的长和宽分别为x,y,剪去部分面积为20.若2x10,则y与x的函数图象是( )
A. B.
C. D.
二、填空题(本大题共4小题,共20分)
如图所示是一蓄水池每小时的排水量V()与排完水池中的水所用时间t(h)之间的函数关系图象.若要5小时排完水池中的水,则每小时的排水量应为 .
继共享单车、共享汽车后,共享运营的时代也催化了另外一种交通工具的流行,那就是共享电动车.共享电动车行驶的总路程s(单位:km)与平均耗电量a(单位:mAh/km)之间满足反比例函数关系s=(k为常数,k0).已知某型号的共享电动车充满电后,以平均耗电量为1800mAh/km的速度行驶,可行驶10km.某次王老师家访时,由于路面不平,平均耗电量为2000mAh/km,则该共享电动车行驶的最远距离为 km.
实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例.一条长为100cm的导线的电阻R()与它的横截面积S()的函数图象如图所示,那么其函数关系式为 ,当S=时,R= .
如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作(m为1~8的整数).函数y=(x<0)的图象为曲线L.
(1)若L过点,则k= ;(2)若L过点,则它必定还过另一点,则m= ;
(3)若曲线L使得~这些点分布在它的两侧,每侧各4个点,则k的整数值有 个.
三、解答题(本大题共3小题,共40分)
在平面直角坐标系xOy中,反比例函数y=(x>0)的图象经过点A(3,4),过点A的直线y=kx+b与x轴、y轴分别交于B,C两点.
(1)求反比例函数的表达式;
(2)若AOB的面积为BOC的面积的2倍,求此直线的函数表达式.
在滑草过程中,小明发现滑道两边形如两条双曲线,如图,点,,,在反比例函数y=(x>0)的图象上,点,,,在反比例函数y=(k>1,x>0)的图象上,y轴,已知点,,的横坐标分别为1,2,,令四边形、的面积分别为、、.
(1)用含k的代数式表示= ;
(2)若=39,则k= .
为了探索函数y=x+(x>0)的图象与性质,我们参照学习函数的过程与方法.列表:
x ... 1 2 3 4 5 ...
y
... 2 ...
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图a所示:
(1)如图a,观察所描出点的分布,用一条光滑曲线将点顺次连接起来,画出函数图象;
(2)已知点(,),(,)在函数图象上,结合表格和函数图象,回答下列问题:
若0<<1,则 ;若1<<,则 ;若=1,则 (填“>”“=”或“<”);
(3)某农户要建造一个如图b所示的长方体无盖水池,其底面积为1平方米,深为1米.已知底面造价为1千元/平方米,侧面造价为0.5千元/平方米.设水池底面一边的长为x米,水池总造价为y千元.
请写出y与x之间的函数关系式;
若该农户预算不超过3.5千元,则水池底面一边的长x应控制在什么范围内
1.【答案】C
2.【答案】B
3.【答案】D
4.【答案】C
5.【答案】C
6.【答案】C
7.【答案】B
8.【答案】A
9.【答案】9.6
10.【答案】9
11.【答案】R=
14.5
12.【答案】-16
5
7
13.【答案】解:(1)反比例函数y=(x>0)的图象经过点A(3,4),
m=34=12,
反比例函数的表达式为y=.
(2)直线y=kx+b过点A,
3k+b=4.
过点A的直线y=kx+b与x轴、y轴分别交于B,C两点,
B(-,0),C(0,b).
AOB的面积为BOC的面积的2倍,
4=2,
b=2,
当b=2时,k=,
当b=-2时,k=2,
此直线的函数表达式为y=x+2或y=2x-2.
14.【答案】(1)(k-1);
(2)761.
15.【答案】解:(1)画函数图象如图所示:
(2)若0<<1,则>;若1<<,则<;若=1,则 =.
故答案为>;<;=.
(3)由题意,得y=1+(2x+)0.5=1+x+(x>0).
观察图象可得,当x2时,x+2.5,即y=1+x+3.5,
答:水池底面一边的长x应控制在x2的范围内.
第2页,共3页
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
