4. 可能性(课件) 人教版数学五年级上册(共28张PPT)
文档属性
| 名称 | 4. 可能性(课件) 人教版数学五年级上册(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-20 09:45:56 | ||
图片预览








文档简介
(共28张PPT)
相传古代有个王国,国王非常阴险而多疑,一位正直的大臣得罪了国王,被判死刑,这个国家世代沿袭着一条奇特的法规:凡是死囚,在砍头之前法官要写两张纸条放到盒子里:一张写着“生”,一张写着“死”,让犯人闭着眼睛摸,你猜猜这个犯人会摸到什么?
可是大法官想让这个大臣死,把“生”字抽出来了,换了一个“死”字。你说这个大臣会怎样?
这个大臣有个好朋友,就把这件事告诉了他,让他想办法。结果他想出了一个办法。猜猜看他想出什么办法来了?
第二天,大臣摸出其中的一张纸条,他看也不看,就把纸条塞到嘴里吃了,咽到肚子里了。大法官着急了,其他大臣说:“别着急,看看盒子里剩下的是什么?就知道他摸到的是什么了。”大法官哑口无言。
生死签的故事
可能性
知识点1:事件发生的确定性和不确定性
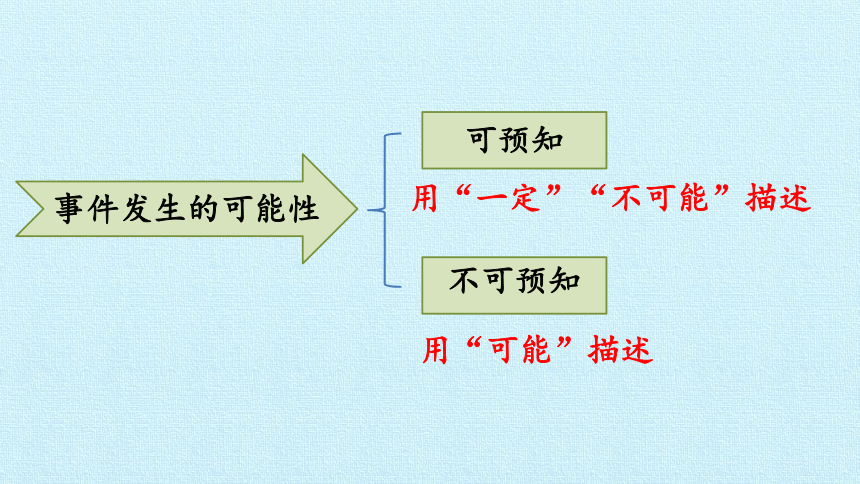
在一定的条件下,一些事件的结果是可以预知的,即可以确定的,我们用“一定”或“不可能”来描述,一些事件是不可预知的,不确定的,我们用“可能”来描述。
事件发生的可能性
可预知
不可预知
用“一定”“不可能”描述
用“可能”描述
有两个盒子,第一个盒子里装有12个黄球,8个黑球,第二个盒子里装有20个白球。
问第一个盒子里可能摸到白球吗?
第一个盒子里可能摸到黑球吗?
第二个盒子里可能摸到白球吗?
答:第一个盒子里不可能摸到白球
第一个盒子里可能摸到黑球
第二个盒子里一定摸到白球。
知识点2:判断事件发生的可能性大小的方法
个体在总数中所占的数量越多,出现的可能性就越大。
1.选一选。
A
B
他闭着眼要摸出 ,在哪个箱子里更容易摸到?
B中 多些,在B箱子里更容易摸到。
2.有十张扑克牌,红桃有5张,黑桃有3张,方块有2张。从十张扑克牌中任意抽一张扑克牌,抽到什么花色的可能性最大,什么花色的可能性最小?
答:抽到红桃的可能性最大,抽到方块的可能性最小。
基础巩固
例1:分别从下面袋子中摸出一个球,摸到白球的可能性各是多少?
一共有4个球
白球有1个
一共有5个球
白球有1个
一共有4个球
白球有3个
即学即练
如图是一个可自由转动的转盘(转盘已被八等分),任意转动转盘,当转盘停止时,指针所指的数是3的倍数的可能性是多少?
一共有8个数
3的倍数有:3、6、3共3个
答:指针所指的数是3的倍数的可能性是 。
例2:给 涂上红、蓝、黄三种颜色,要使掷出红色的面的可能性比蓝色大,比黄色小,可以怎样涂?
由题意可得出:
蓝色的面最少,黄色的面最多。而正方体只有6个面,分为三部分:1+2+3=6,因此蓝色有1个面,红色有2个面,黄色有3个面。
蓝色:
红色:
黄色:
涂1面
涂2面
涂3面
即学即练
在下面转盘上涂上红色和蓝色,使指针停在蓝色区域的可能性大,请设计一种涂色方案。
由题意可得出:
蓝色的区域多,红色的区域少。
蓝色涂5块,红色涂3块。
你还有其他的涂色方案吗?
例3:掷一骰子,6个面分别标着1~6的数字,标着 “3” 的面朝上的可能性是多少?朝上的面是单数的可能性又是多少?
3
即学即练
口袋有大小相同的6个球,3个红球,3个白球,从中任意摸出两个球。
(1)都摸到红球的可能性是( )。
(2)都摸到白球的可能性是( )。
(3)摸到一个白球,一个红球的可能性是( )。
从6个球中任意摸出两个球,只有3种可能:两个球都是红色、两个球都是白色、一个球是红色一个球是白色。
小结
事件发生的可能性有大小之分,可能性大小通常表示方法:
可能发生该类情况数占总发生情况数的几分之几。
综合拓展
例4:有三张写着数字的卡片,如下图。
小奥:“用它们摆三位数,如果摆出双数我胜,摆出单数你胜。”
朋朋:“你的规则好像不公平……”
他们两人获胜的可能性各是几分之几?小奥的规则是否公平?
2
3
6
你认为规则公平吗?
还是先写出卡片能摆的三位数有多少,分别计算出两人获胜的可能性。
236
263
326
362
623
632
一共能摆出6个三位数
其中双数有4个,单数有2个。
小奥获胜的可能性是
朋朋获胜的可能性是
答:因为他们获胜的可能性不相等,所以小奥的规则不公平。
即学即练
有四张卡片,上面分别写有0,3,1,2,任意取三张摆成一个三位数。
摆出末尾是0的数的可能性是多少?
摆出中间是0的数的可能性是多少?
四张卡片任意取三张摆成一个三位数共有18种情况
摆出末尾是0的数共有6种情况:
120、130、210、230、310、320
摆出中间是0的数共有6种情况:
102、103、201、203、301、302
答:摆出末尾是0的数的可能性是 ,摆出中间是0的数的可能性是 。
例5:下面有五张扑克牌,三张红桃,两张梅花。
(1)翻过去洗好后任意摸出两张,两张是红桃,小军赢;两张是梅花,玲玲赢;
这两个规则哪个公平?哪个不公平?说明理由,并写出来。
(2)翻过去洗好后任意摸出两张,和大于3,玲玲赢;和小于或等于3,小军赢。
(1)翻过去洗好后任意摸出两张,两张是红桃,小军赢;两张是梅花,玲玲赢;
(1)翻过去洗好后任意摸出两张,两张是红桃,小军赢;两张是梅花,玲玲赢;
任意摸出两张,一共有10种情况。
两张是红桃的有3种情况,所以小军赢的可能性是
两张是梅花的有1种情况,所以玲玲赢的可能性是
因为他们获胜的可能性不相等,
所以(1)规则不公平。
(2)翻过去洗好后任意摸出两张,和大于3,玲玲赢;和小于或等于3,小军赢。
(2)翻过去洗好后任意摸出两张,和大于3,玲玲赢;和小于或等于3,小军赢。
和:3、4、2、3、5、3、4、4、5、3
和大于3的有5种情况,所以玲玲赢的可能性是
和小于3或等于3的有5种情况,所以小军赢的可能性是
因为他们获胜的可能性相等,
所以(2)规则是公平的。
即学即练
在抛硬币游戏中,如果将一枚均匀的硬币连续抛掷3次,那么三次中不接连出现正面的可能性是多少?
将一枚均匀的硬币连续抛掷3次共有8种情况:
正正正、正正反、正反正、反正正、
正反反、反正反、反反正、反反反。
三次中不接连出现正面共有5种情况:
正反正、正反反、反正反、反反正、反反反。
答:三次中不接连出现正面的可能性是 。
例6:看竖式,在括号里填“可能”或“不可能”。
被除数( )是16
( )是26
( )是36
你敢自己挑战吗?
例6:看竖式,在括号里填“可能”或“不可能”。
被除数( )是16
( )是26
( )是36
16能被4整除
可能
26不能被4整除
不可能
36能被4整除
可能
事件发生的可能性有大小之分,可能性大小通常表示方法:
可能发生该类情况数占总发生情况数的几分之几。
相传古代有个王国,国王非常阴险而多疑,一位正直的大臣得罪了国王,被判死刑,这个国家世代沿袭着一条奇特的法规:凡是死囚,在砍头之前法官要写两张纸条放到盒子里:一张写着“生”,一张写着“死”,让犯人闭着眼睛摸,你猜猜这个犯人会摸到什么?
可是大法官想让这个大臣死,把“生”字抽出来了,换了一个“死”字。你说这个大臣会怎样?
这个大臣有个好朋友,就把这件事告诉了他,让他想办法。结果他想出了一个办法。猜猜看他想出什么办法来了?
第二天,大臣摸出其中的一张纸条,他看也不看,就把纸条塞到嘴里吃了,咽到肚子里了。大法官着急了,其他大臣说:“别着急,看看盒子里剩下的是什么?就知道他摸到的是什么了。”大法官哑口无言。
生死签的故事
可能性
知识点1:事件发生的确定性和不确定性
在一定的条件下,一些事件的结果是可以预知的,即可以确定的,我们用“一定”或“不可能”来描述,一些事件是不可预知的,不确定的,我们用“可能”来描述。
事件发生的可能性
可预知
不可预知
用“一定”“不可能”描述
用“可能”描述
有两个盒子,第一个盒子里装有12个黄球,8个黑球,第二个盒子里装有20个白球。
问第一个盒子里可能摸到白球吗?
第一个盒子里可能摸到黑球吗?
第二个盒子里可能摸到白球吗?
答:第一个盒子里不可能摸到白球
第一个盒子里可能摸到黑球
第二个盒子里一定摸到白球。
知识点2:判断事件发生的可能性大小的方法
个体在总数中所占的数量越多,出现的可能性就越大。
1.选一选。
A
B
他闭着眼要摸出 ,在哪个箱子里更容易摸到?
B中 多些,在B箱子里更容易摸到。
2.有十张扑克牌,红桃有5张,黑桃有3张,方块有2张。从十张扑克牌中任意抽一张扑克牌,抽到什么花色的可能性最大,什么花色的可能性最小?
答:抽到红桃的可能性最大,抽到方块的可能性最小。
基础巩固
例1:分别从下面袋子中摸出一个球,摸到白球的可能性各是多少?
一共有4个球
白球有1个
一共有5个球
白球有1个
一共有4个球
白球有3个
即学即练
如图是一个可自由转动的转盘(转盘已被八等分),任意转动转盘,当转盘停止时,指针所指的数是3的倍数的可能性是多少?
一共有8个数
3的倍数有:3、6、3共3个
答:指针所指的数是3的倍数的可能性是 。
例2:给 涂上红、蓝、黄三种颜色,要使掷出红色的面的可能性比蓝色大,比黄色小,可以怎样涂?
由题意可得出:
蓝色的面最少,黄色的面最多。而正方体只有6个面,分为三部分:1+2+3=6,因此蓝色有1个面,红色有2个面,黄色有3个面。
蓝色:
红色:
黄色:
涂1面
涂2面
涂3面
即学即练
在下面转盘上涂上红色和蓝色,使指针停在蓝色区域的可能性大,请设计一种涂色方案。
由题意可得出:
蓝色的区域多,红色的区域少。
蓝色涂5块,红色涂3块。
你还有其他的涂色方案吗?
例3:掷一骰子,6个面分别标着1~6的数字,标着 “3” 的面朝上的可能性是多少?朝上的面是单数的可能性又是多少?
3
即学即练
口袋有大小相同的6个球,3个红球,3个白球,从中任意摸出两个球。
(1)都摸到红球的可能性是( )。
(2)都摸到白球的可能性是( )。
(3)摸到一个白球,一个红球的可能性是( )。
从6个球中任意摸出两个球,只有3种可能:两个球都是红色、两个球都是白色、一个球是红色一个球是白色。
小结
事件发生的可能性有大小之分,可能性大小通常表示方法:
可能发生该类情况数占总发生情况数的几分之几。
综合拓展
例4:有三张写着数字的卡片,如下图。
小奥:“用它们摆三位数,如果摆出双数我胜,摆出单数你胜。”
朋朋:“你的规则好像不公平……”
他们两人获胜的可能性各是几分之几?小奥的规则是否公平?
2
3
6
你认为规则公平吗?
还是先写出卡片能摆的三位数有多少,分别计算出两人获胜的可能性。
236
263
326
362
623
632
一共能摆出6个三位数
其中双数有4个,单数有2个。
小奥获胜的可能性是
朋朋获胜的可能性是
答:因为他们获胜的可能性不相等,所以小奥的规则不公平。
即学即练
有四张卡片,上面分别写有0,3,1,2,任意取三张摆成一个三位数。
摆出末尾是0的数的可能性是多少?
摆出中间是0的数的可能性是多少?
四张卡片任意取三张摆成一个三位数共有18种情况
摆出末尾是0的数共有6种情况:
120、130、210、230、310、320
摆出中间是0的数共有6种情况:
102、103、201、203、301、302
答:摆出末尾是0的数的可能性是 ,摆出中间是0的数的可能性是 。
例5:下面有五张扑克牌,三张红桃,两张梅花。
(1)翻过去洗好后任意摸出两张,两张是红桃,小军赢;两张是梅花,玲玲赢;
这两个规则哪个公平?哪个不公平?说明理由,并写出来。
(2)翻过去洗好后任意摸出两张,和大于3,玲玲赢;和小于或等于3,小军赢。
(1)翻过去洗好后任意摸出两张,两张是红桃,小军赢;两张是梅花,玲玲赢;
(1)翻过去洗好后任意摸出两张,两张是红桃,小军赢;两张是梅花,玲玲赢;
任意摸出两张,一共有10种情况。
两张是红桃的有3种情况,所以小军赢的可能性是
两张是梅花的有1种情况,所以玲玲赢的可能性是
因为他们获胜的可能性不相等,
所以(1)规则不公平。
(2)翻过去洗好后任意摸出两张,和大于3,玲玲赢;和小于或等于3,小军赢。
(2)翻过去洗好后任意摸出两张,和大于3,玲玲赢;和小于或等于3,小军赢。
和:3、4、2、3、5、3、4、4、5、3
和大于3的有5种情况,所以玲玲赢的可能性是
和小于3或等于3的有5种情况,所以小军赢的可能性是
因为他们获胜的可能性相等,
所以(2)规则是公平的。
即学即练
在抛硬币游戏中,如果将一枚均匀的硬币连续抛掷3次,那么三次中不接连出现正面的可能性是多少?
将一枚均匀的硬币连续抛掷3次共有8种情况:
正正正、正正反、正反正、反正正、
正反反、反正反、反反正、反反反。
三次中不接连出现正面共有5种情况:
正反正、正反反、反正反、反反正、反反反。
答:三次中不接连出现正面的可能性是 。
例6:看竖式,在括号里填“可能”或“不可能”。
被除数( )是16
( )是26
( )是36
你敢自己挑战吗?
例6:看竖式,在括号里填“可能”或“不可能”。
被除数( )是16
( )是26
( )是36
16能被4整除
可能
26不能被4整除
不可能
36能被4整除
可能
事件发生的可能性有大小之分,可能性大小通常表示方法:
可能发生该类情况数占总发生情况数的几分之几。
