25.1.1随机事件 人教版初中数学九年级上册 课件(共21张PPT)
文档属性
| 名称 | 25.1.1随机事件 人教版初中数学九年级上册 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 09:22:27 | ||
图片预览







文档简介
(共21张PPT)
第二十五章 概率初步
25.1.1 随机事件
学习目标:
1.理解必然事件、不可能事件、随机事件的概念;
2.通过实验操作等体会随机事件发生的可能性是有
大小的.
学习重点:
随机事件的特点.
在现实世界中,我们经常遇到无法预料事情发生结果的情况.
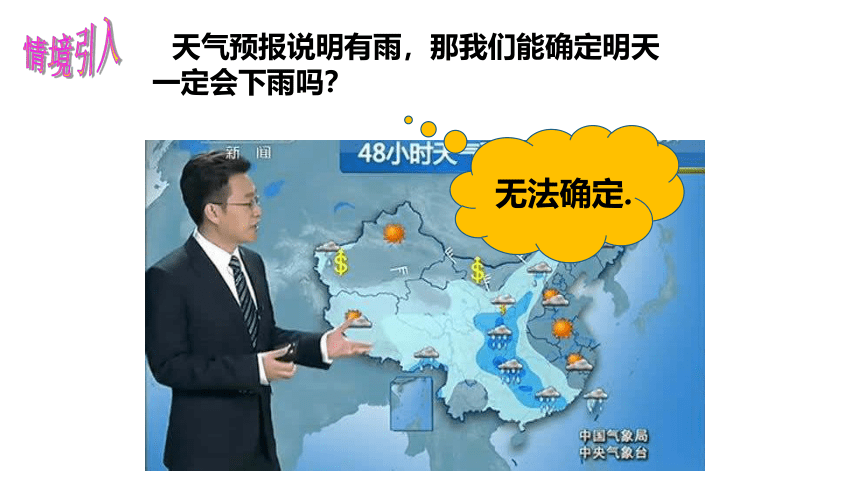
天气预报说明有雨,那我们能确定明天一定会下雨吗?
无法确定.
情境引入
在某一时刻拨打查号台(114),线路一定接通吗?
无法确定.
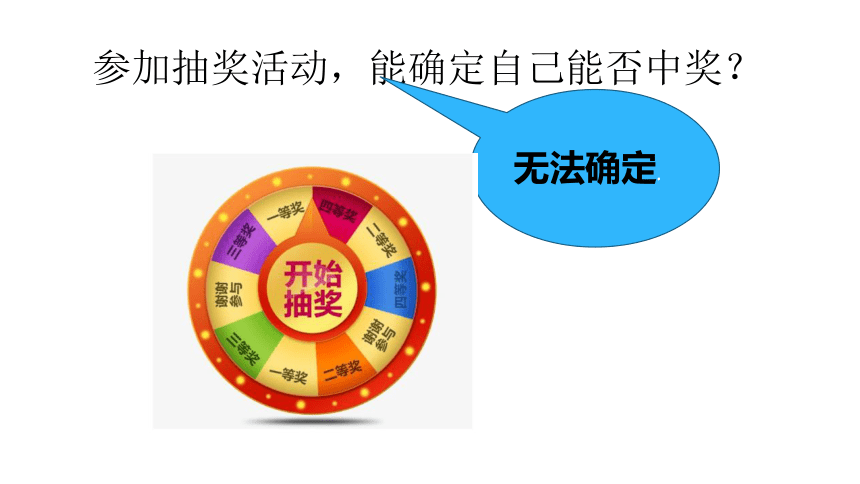
参加抽奖活动,能确定自己能否中奖?
无法确定.
这些事情的发生都给我们不确定的印象.
俗话说:“天有不测风云”,也就是说世界上有很
多事情具有偶然性,人们不能事先判定这些事情是否会
发生.试根据事件发生可能性的不同,把下面的 8 个事
件分类:
思考
(1)某人的体温是 100 ℃
(2) a 2 +b 2 = -1(其中 a,b 都是实数);
(3)太阳从东边升起;
(4)经过城市中某一有交通信号灯的路口,遇到绿灯;
(5)一元二次方程 x 2 + 2x + 3 = 0 无实数解.
(6)掷一枚骰子,向上的一面是 3 点;
(7)鱼离开水可以正常存活 2天;
(8)篮球队员在罚线上投篮一次,未投中.
必然会发生的事件有_______________;
不可能发生的事件有_______________;
可能发生也可能不发生的事件有______________.
思考
掷一枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数。请做这样的小试验:掷一次骰子,在骰子向上的一面上,
(1)可能出现哪些点数?
(2)出现的点数大于0吗?
(3)出现的点数会是7吗?
(4)出现的点数会是5吗?
做简单的小试验:
从1到6 的每一个点数都有可能出现,所有可能的点数共有6种,但事先无法预料掷一次骰子会出现哪一种结果.
出现的点数肯定大于0.
出现的点数不可能是7.
出现的点数可能是5,也可能不是5,事先无法确定.
1、必然事件:在一定条件下,必然发生的事件.
2、不可能事件:在一定条件下,一定不会发生的事件.
3、随机事件:在一定条件下可能发生,也可能不发生的事件.
归纳总结:
你能举一些随机事件的例子吗?
指出下列事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件.
(1)通常加热到100℃时,水沸腾.
(2)懒求队员在罚球线上投篮一次,未投中.
(3)掷一次骰子,向上一面的点数是6.
(4)某个数的绝对值小于0°
(5)三个人性别各不相同.
(6)射击运动员射击一次,命中靶心.
必然事件
随机事件
随机事件
不可能事件
不可能事件
随机事件
做一做
动手做一做,一起交流:
例: 袋子中装有4个黑球,2个白球,这些球的形状,大小,质地等完全相同,即除颜色外无其他差别。在看不到球的条件下,随机从袋子中摸出1个球。
(1)这个球是白球还是黑球?
(2)如果两种球都有可能被摸出,那么摸出黑球和摸出白球的可能性一样大吗?
为了验证你的想法,动手摸一下吧!每名同学随机从袋子中摸出1个球,记下球的颜色,然后把球重新放回袋子并摇匀。汇总全班同学摸球的结果并把结果填在下表中。
球的颜色 黑球 白球
摸取次数
一般地,随机事件发生的可能性是有大小的。
思考:
能否通过改变袋子中某种颜色的球的数量,使“摸出黑球”和“摸出白球”的可能性大小相同?
1.已知地球表面陆地面积与海洋面积的比约为3:7。如果宇宙飞来一块陨石落在地球上,“落在陆地上”与“落在海里”哪种可能性大?
课堂练习
“落在海里”的可能性大
2.桌上倒扣着背面图案相同的5张扑克牌,其中3张黑桃,2张红桃。从中随机抽取1张。
(1)能够事先确定抽取的扑克牌的花色吗?
(2) 你认为抽到哪种花色的可能性大?
(3)能否通过改变某种花色的扑克牌的数量,使“抽到黑桃”和“抽到红桃”的可能性大小相同?
3.列举一些生活中的随机事件,不可能事件和必然事件的例子。
4.一个布袋中有三个白球,七个黄球,他们除了颜色外其余都相同,现在从中摸出四个球。
事件①:摸出四个黄球
事件②:摸出四个白球
事件③:摸出四个球中,至少有一个黄球
事件④:摸出四个球中,至少有一个白球
其中,必然事件有
随机事件有
不可能事件有
①
②
③
④
(3) -a是负数。属于 事件。
必然事件
(2) ,-a是负数。属于不可能事件。
随 机
(1) a2+1>0, 属于 。
a≤0
5.填空题
课堂小结
1、必然事件:在一定条件下,必然发生的事件.
2、不可能事件:在一定条件下,一定不会发生的事件.
3、随机事件:在一定条件下可能发生,也可能不发生的事件.
确定性事件
谢谢!
第二十五章 概率初步
25.1.1 随机事件
学习目标:
1.理解必然事件、不可能事件、随机事件的概念;
2.通过实验操作等体会随机事件发生的可能性是有
大小的.
学习重点:
随机事件的特点.
在现实世界中,我们经常遇到无法预料事情发生结果的情况.
天气预报说明有雨,那我们能确定明天一定会下雨吗?
无法确定.
情境引入
在某一时刻拨打查号台(114),线路一定接通吗?
无法确定.
参加抽奖活动,能确定自己能否中奖?
无法确定.
这些事情的发生都给我们不确定的印象.
俗话说:“天有不测风云”,也就是说世界上有很
多事情具有偶然性,人们不能事先判定这些事情是否会
发生.试根据事件发生可能性的不同,把下面的 8 个事
件分类:
思考
(1)某人的体温是 100 ℃
(2) a 2 +b 2 = -1(其中 a,b 都是实数);
(3)太阳从东边升起;
(4)经过城市中某一有交通信号灯的路口,遇到绿灯;
(5)一元二次方程 x 2 + 2x + 3 = 0 无实数解.
(6)掷一枚骰子,向上的一面是 3 点;
(7)鱼离开水可以正常存活 2天;
(8)篮球队员在罚线上投篮一次,未投中.
必然会发生的事件有_______________;
不可能发生的事件有_______________;
可能发生也可能不发生的事件有______________.
思考
掷一枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数。请做这样的小试验:掷一次骰子,在骰子向上的一面上,
(1)可能出现哪些点数?
(2)出现的点数大于0吗?
(3)出现的点数会是7吗?
(4)出现的点数会是5吗?
做简单的小试验:
从1到6 的每一个点数都有可能出现,所有可能的点数共有6种,但事先无法预料掷一次骰子会出现哪一种结果.
出现的点数肯定大于0.
出现的点数不可能是7.
出现的点数可能是5,也可能不是5,事先无法确定.
1、必然事件:在一定条件下,必然发生的事件.
2、不可能事件:在一定条件下,一定不会发生的事件.
3、随机事件:在一定条件下可能发生,也可能不发生的事件.
归纳总结:
你能举一些随机事件的例子吗?
指出下列事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件.
(1)通常加热到100℃时,水沸腾.
(2)懒求队员在罚球线上投篮一次,未投中.
(3)掷一次骰子,向上一面的点数是6.
(4)某个数的绝对值小于0°
(5)三个人性别各不相同.
(6)射击运动员射击一次,命中靶心.
必然事件
随机事件
随机事件
不可能事件
不可能事件
随机事件
做一做
动手做一做,一起交流:
例: 袋子中装有4个黑球,2个白球,这些球的形状,大小,质地等完全相同,即除颜色外无其他差别。在看不到球的条件下,随机从袋子中摸出1个球。
(1)这个球是白球还是黑球?
(2)如果两种球都有可能被摸出,那么摸出黑球和摸出白球的可能性一样大吗?
为了验证你的想法,动手摸一下吧!每名同学随机从袋子中摸出1个球,记下球的颜色,然后把球重新放回袋子并摇匀。汇总全班同学摸球的结果并把结果填在下表中。
球的颜色 黑球 白球
摸取次数
一般地,随机事件发生的可能性是有大小的。
思考:
能否通过改变袋子中某种颜色的球的数量,使“摸出黑球”和“摸出白球”的可能性大小相同?
1.已知地球表面陆地面积与海洋面积的比约为3:7。如果宇宙飞来一块陨石落在地球上,“落在陆地上”与“落在海里”哪种可能性大?
课堂练习
“落在海里”的可能性大
2.桌上倒扣着背面图案相同的5张扑克牌,其中3张黑桃,2张红桃。从中随机抽取1张。
(1)能够事先确定抽取的扑克牌的花色吗?
(2) 你认为抽到哪种花色的可能性大?
(3)能否通过改变某种花色的扑克牌的数量,使“抽到黑桃”和“抽到红桃”的可能性大小相同?
3.列举一些生活中的随机事件,不可能事件和必然事件的例子。
4.一个布袋中有三个白球,七个黄球,他们除了颜色外其余都相同,现在从中摸出四个球。
事件①:摸出四个黄球
事件②:摸出四个白球
事件③:摸出四个球中,至少有一个黄球
事件④:摸出四个球中,至少有一个白球
其中,必然事件有
随机事件有
不可能事件有
①
②
③
④
(3) -a是负数。属于 事件。
必然事件
(2) ,-a是负数。属于不可能事件。
随 机
(1) a2+1>0, 属于 。
a≤0
5.填空题
课堂小结
1、必然事件:在一定条件下,必然发生的事件.
2、不可能事件:在一定条件下,一定不会发生的事件.
3、随机事件:在一定条件下可能发生,也可能不发生的事件.
确定性事件
谢谢!
同课章节目录
