垂径定理（2）

(共16张PPT)
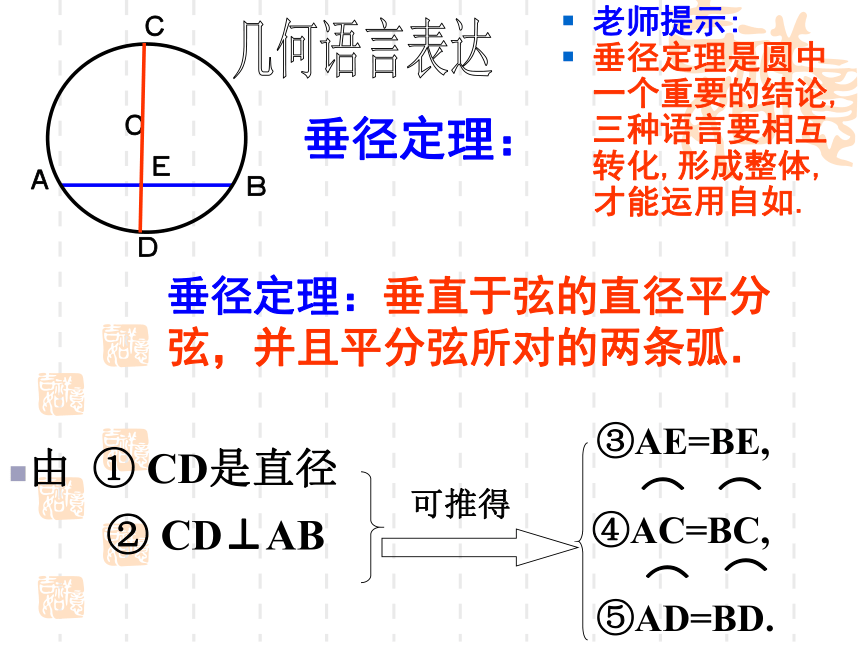
③AE=BE,
由 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
⑤AD=BD.
⌒
⌒
④AC=BC,
Ｄ
Ｃ
Ａ
Ｂ
Ｅ
Ｏ
垂径定理：
老师提示:
垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧．
判断下列说法的正误
①平分弧的直径必平分弧所对的弦( )
　②平分弦的直线必垂直弦( )
③垂直于弦的直径平分这条弦( )
④平分弦的直径垂直于这条弦( )
⑤弦的垂直平分线是圆的直径( )
⑥平分弦所对的一条弧的直径必垂直
这条弦 ( )
⑦在圆中，如果一条直线经过圆心且平分弦，必平分此弦所对的弧( )
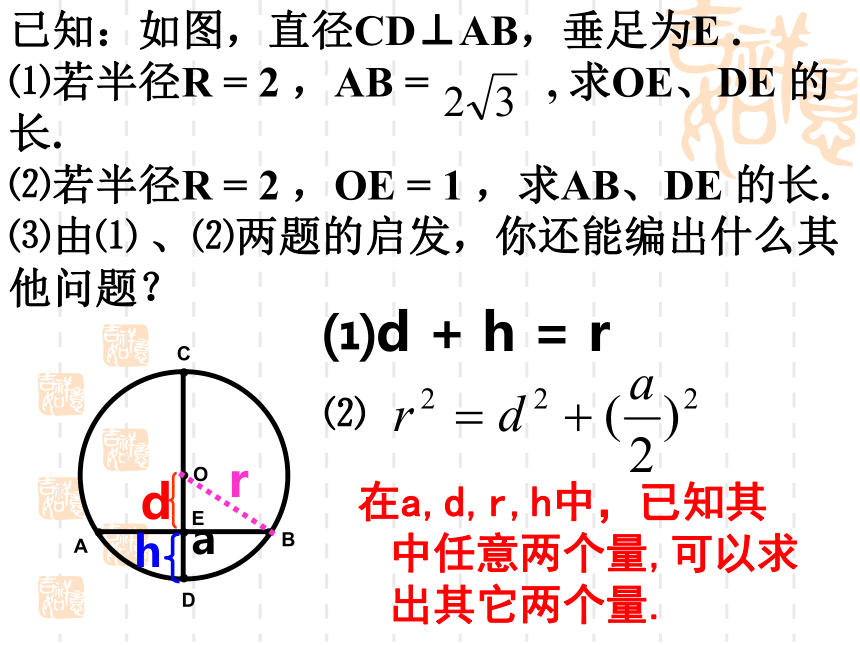
在a,d,r,h中，已知其中任意两个量,可以求出其它两个量.
⑴d + h = r
⑵
已知：如图，直径CD⊥AB，垂足为E .
⑴若半径R = 2 ，AB = , 求OE、DE 的长.
⑵若半径R = 2 ，OE = 1 ，求AB、DE 的长.
⑶由⑴ 、⑵两题的启发，你还能编出什么其他问题？
d
r
a
h
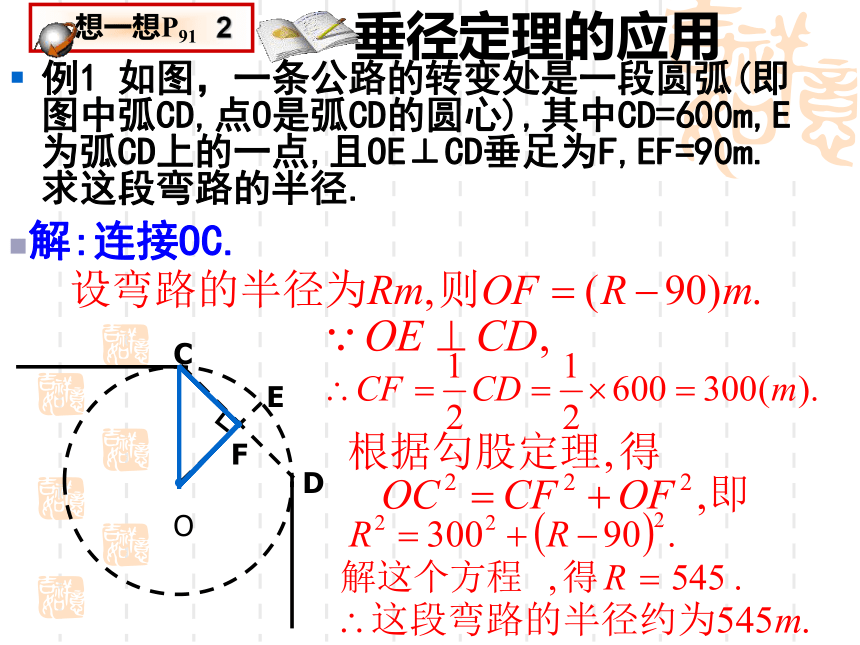
垂径定理的应用
例1 如图，一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径.
想一想P91
2
解:连接OC.
●
O
C
D
E
F
┗
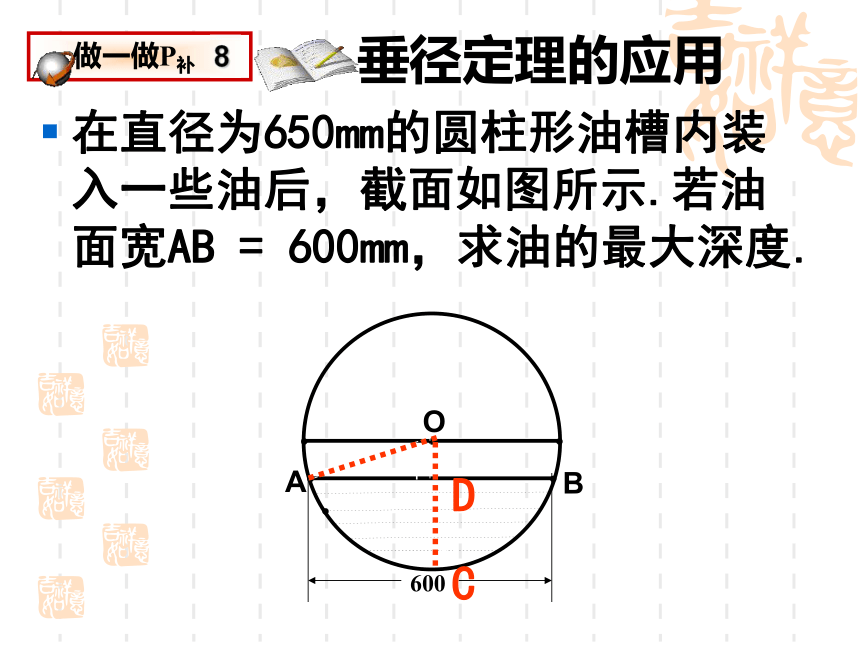
垂径定理的应用
在直径为650mm的圆柱形油槽内装入一些油后，截面如图所示.若油面宽AB = 600mm，求油的最大深度.
做一做P补
8
E
D
┌
600
D
C
在直径为650mm的圆柱形油槽内装入一些油后，截面如图所示.若油面宽AB = 600mm，求油的最大深度.
B
A
O
600
650
D
C
例、某地有一座圆弧形拱桥圆心为Ｏ，桥下水面宽度为７.2 m ，过O作OC⊥AB于D，交圆弧于C，CD=2.4m，现有一艘宽3m，船舱顶部为方形并高出水面（AB）2m的货船要经过拱桥，此货船能否顺利通过这座拱桥？
C
N
M
A
E
H
F
B
D
O
船能过拱桥吗
解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.连结OA、ON，由题设得
在Rt△OAD中，由勾股定理，得
解得 R≈3.9（m）.
在Rt△ONH中，由勾股定理，得
∴此货船能顺利通过这座拱桥.
C
N
M
A
E
H
F
B
D
O
说出你这节课的收获和体验，让大家与你一起分享！！！
1、要把实际问题转变成一个数学问题来解决.
2、熟练地运用垂径定理及其推论、勾股定理，并用方程的思想来解决问题.
3、对于一个圆中的弦长a、圆心到弦的距离d、圆半径r、弓形高h，这四个量中，只要已知其中任意两个量，就可以求出另外两个量，如图有：
⑴d + h = r
⑵
d
r
a
h
别忘记还有我哟！！
教材95页习题24.1
　　　 7、8　；
作业：
结束寄语
不学自知,不问自晓,古今行事,未之有也.
下课了!