1.5.1有理数的乘方课件
图片预览






文档简介
(共25张PPT)
a
边长为a的正方形的面积是 a·a,简记作a2,读作a的平方(或二次方)
棱长为a的正方体的体积是a·a·a,简记作a3,读作a的立方(或三次方)
a
2个 相加可记为:
边长为 的正方形的面积可记为:
3个 相加可为:
棱长为 的正方体的体积可记为:
个 相加可记为:
个 相乘又可记为:
{
n个
an
求n个相同因数的积的运算,叫做乘方
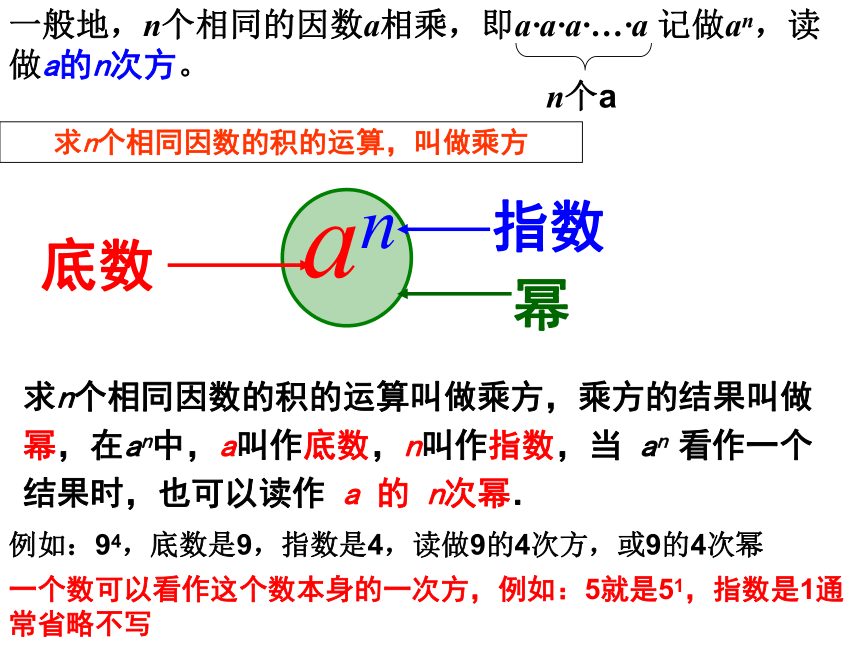
一般地,n个相同的因数a相乘,即a·a·a·…·a 记做an,读做a的n次方。
n个a
例如:94,底数是9,指数是4,读做9的4次方,或9的4次幂
一个数可以看作这个数本身的一次方,例如:5就是51,指数是1通常省略不写
an
底数
指数
幂
求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂,在an中,a叫作底数,n叫作指数,当 an 看作一个结果时,也可以读作 a 的 n次幂.
1.把下列各式写成乘方运算的形式,并指出底数,指数各是什么
1. 5×5×5×5×5
2. (-1.3)(-1.3)(-1.3)(-1.3)
4. m·m ·m ·… ·m
2a个
4、
(- )3
赏析例一
计算:
1、 (-4)3
2、(-2)4
2
3
(- )2
1
5
3、
你发现负数的幂的正负有什么规律?
解: 1、(-4)3=
-
8
27
2
3
(- )3
(- )2
1
5
2
3
(- )
2
3
(- )
2
3
(- )
(- )
1
5
(- )
1
5
=
× ×
=
=
×
=
1
25
3、
4、
2、(-2)4=(-2) ×(-2) ×(-2) ×(-2)=16
(-4) ×(-4) ×(-4)
=-64
当指数是——数时,负数的幂是—数。
当指数是——数时,负数的幂是—数。
奇
负
偶
正
4、
( )3
变形训练
计算:
1、 43
2、24
2
3
( )2
1
5
3、
你发现正数和0的幂有什么规律?
5、 05
=64
=16
=
8
27
=
1
25
=0
正数的任何次幂都是正数,
0的任何正整数次幂都是0。
(1)正数的任何次幂是正数;
(2)负数的偶次幂是正数;负数的奇次幂是负数;
(3)0的任何次幂等于零; 1的任何次幂等于1.
乘方运算的符号规律
3.计算:
1、(-1)10
2、(-1)7
3、83
6、(- )4
1
2
5、
4、-24
2
3
3
= -1
= 1
= 512
=
16
1
=-16
=—
8
3
4.-32与(-3)2 结果相等吗?
- 32读作的32相反数,结果是-9;而(-3)2 读作 -3的平方,结果是9 。
5.请你说说下列各数表示什么?它们一样吗?
(1)23 与 32
(2) 与
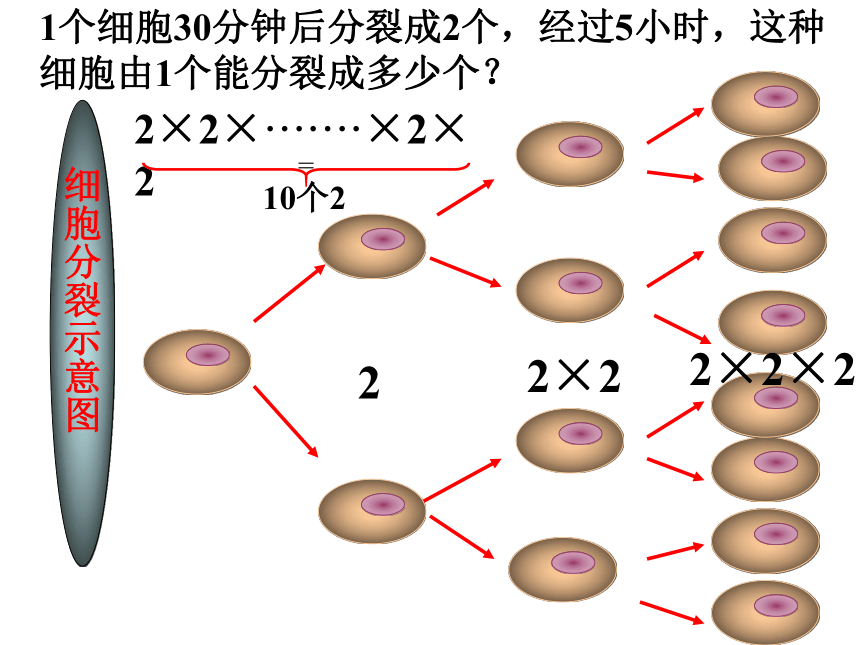
细胞分裂示意图
1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?
2
2×2
2×2×2
2×2×·······×2×2
=
10个2
显示:
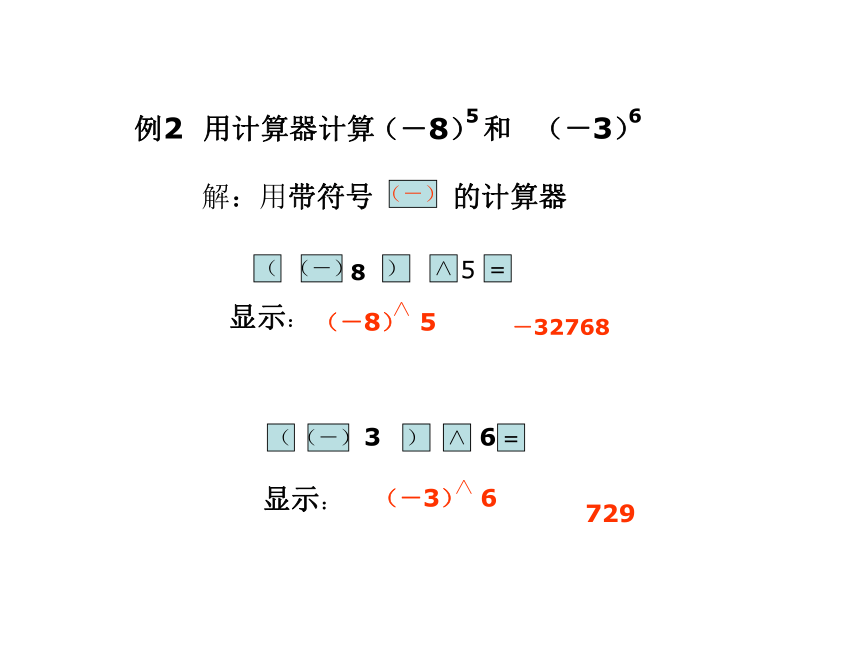
(-8) 5
-32768
(
(-)
)
=
3
6
解:用带符号 的计算器
(-)
(
(-)
)
8
=
5
显示:
(-3) 6
729
例2 用计算器计算 和
(-8)
5
(-3)
6
用带符号转 换键 的计算器
+/-
+/-
8
5
=
显示:-32768
显示: 729
所以 =-32786 =729
(-3)
6
(-8)
5
+/-
=
3
6
(-1)
10
8
3
(-5)
3
0.1
3
(-10)4
(-10)5
(-1)
7
练习
1、计算
(1) (2) (3) (4)
(5) (6) (7) (8)
(-1)
7
(-1)
10
8
3
(-5)
3
0.1
3
1
2
—
(- )
4
(-10)4
(-10)5
1
2
—
(- )
4
解:
=1
=-1
=512
=-125
=0.001
1
16
= —
=10000
=-100000
3.判断下列各题是否正确:
( )① ;
( )② ;
( )③ ;
( )④ ;
对
错
错
错
4.计算:
先乘方、再乘除
运用新知 体会成功:
(1)、(-5)3 (2)、
(3)、5×23 (4)、(5×2)3
(5)、(-2)2 ×(-3)2
(6)、(-2)3÷ 22
-125
256
81
40
1000
36
-2
1.先乘方、再乘除、最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
2×(-3)3-4×(-3)+15
(-2)3+(-3)×[(-4)2+2]-(-3)2÷(-2)
例3 计算
解(1)第①行数是
-2,(-2)2 ,(-2)3 ,(-2)4 , …
(2)对比①②两行中位置对应的数,你有什么发现?第②行数是第①行相应的数加2,即
-2+2,(-2)2+2,(-2)3+2,(-2)4+2,…
例4 观察下面三行数:
-2,4,-8,16,-32,64,… ①
0,6,-6,18,-30,66,… ②
-1,2,-4,8,-16,32,… ③
(1)第①行数按什么规律排列
(2)第②③行数与第第①行数分别有什么关系?
(3)取每行数的第10个数,计算这三个数的和。
对比①③两行中位置对应的数,你有什么发现?第③行是第①行相应的数的0.5倍,即
-2X0.5,(-2)2X0.5,(-2)3X0.5,(-2)4X0.5,…
(3)每行数中的第10个数的和是
(-2)10+[(-2)10+2]+(-2)10X0.5
=1024+(1024+2)+1024X0.5
=1024+1026+512=2562
-2,4,-8,16,-32,64,… ①
0,6,-6,18,-30,66,… ②
-1,2,-4,8,-16,32,… ③
练习
计算:
(1)(-1)10×2+(-2)3÷4
(2)
思路:先算乘方,再算乘除,再算加减
解:原式=1×2+(-8)÷4
=2+(-2)=0
思路:先算乘方,再算乘法,再算减
思路:先算括号内的运算,再从左到右
解:原式=10000+(16-12X2)
=10000-8=9992
(4)(-10)4+[(-4)2-(3+32)X2]
(3)
有理数的混合运算法则
一般地,我们有:n个相同的因数a相乘,即a a … a,记作an
n个
幂
指数
底数
负数的奇次幂是负数
负数的偶次幂是正数
小结:
1.先乘方、再乘除、最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
3.若a为任意有理数,则a2一定是( )
A.正数 B.负数
C.非负数 D.非正数
B
C
结 束 寄 语
不经历风雨,怎能见彩虹!
下 课
a
边长为a的正方形的面积是 a·a,简记作a2,读作a的平方(或二次方)
棱长为a的正方体的体积是a·a·a,简记作a3,读作a的立方(或三次方)
a
2个 相加可记为:
边长为 的正方形的面积可记为:
3个 相加可为:
棱长为 的正方体的体积可记为:
个 相加可记为:
个 相乘又可记为:
{
n个
an
求n个相同因数的积的运算,叫做乘方
一般地,n个相同的因数a相乘,即a·a·a·…·a 记做an,读做a的n次方。
n个a
例如:94,底数是9,指数是4,读做9的4次方,或9的4次幂
一个数可以看作这个数本身的一次方,例如:5就是51,指数是1通常省略不写
an
底数
指数
幂
求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂,在an中,a叫作底数,n叫作指数,当 an 看作一个结果时,也可以读作 a 的 n次幂.
1.把下列各式写成乘方运算的形式,并指出底数,指数各是什么
1. 5×5×5×5×5
2. (-1.3)(-1.3)(-1.3)(-1.3)
4. m·m ·m ·… ·m
2a个
4、
(- )3
赏析例一
计算:
1、 (-4)3
2、(-2)4
2
3
(- )2
1
5
3、
你发现负数的幂的正负有什么规律?
解: 1、(-4)3=
-
8
27
2
3
(- )3
(- )2
1
5
2
3
(- )
2
3
(- )
2
3
(- )
(- )
1
5
(- )
1
5
=
× ×
=
=
×
=
1
25
3、
4、
2、(-2)4=(-2) ×(-2) ×(-2) ×(-2)=16
(-4) ×(-4) ×(-4)
=-64
当指数是——数时,负数的幂是—数。
当指数是——数时,负数的幂是—数。
奇
负
偶
正
4、
( )3
变形训练
计算:
1、 43
2、24
2
3
( )2
1
5
3、
你发现正数和0的幂有什么规律?
5、 05
=64
=16
=
8
27
=
1
25
=0
正数的任何次幂都是正数,
0的任何正整数次幂都是0。
(1)正数的任何次幂是正数;
(2)负数的偶次幂是正数;负数的奇次幂是负数;
(3)0的任何次幂等于零; 1的任何次幂等于1.
乘方运算的符号规律
3.计算:
1、(-1)10
2、(-1)7
3、83
6、(- )4
1
2
5、
4、-24
2
3
3
= -1
= 1
= 512
=
16
1
=-16
=—
8
3
4.-32与(-3)2 结果相等吗?
- 32读作的32相反数,结果是-9;而(-3)2 读作 -3的平方,结果是9 。
5.请你说说下列各数表示什么?它们一样吗?
(1)23 与 32
(2) 与
细胞分裂示意图
1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?
2
2×2
2×2×2
2×2×·······×2×2
=
10个2
显示:
(-8) 5
-32768
(
(-)
)
=
3
6
解:用带符号 的计算器
(-)
(
(-)
)
8
=
5
显示:
(-3) 6
729
例2 用计算器计算 和
(-8)
5
(-3)
6
用带符号转 换键 的计算器
+/-
+/-
8
5
=
显示:-32768
显示: 729
所以 =-32786 =729
(-3)
6
(-8)
5
+/-
=
3
6
(-1)
10
8
3
(-5)
3
0.1
3
(-10)4
(-10)5
(-1)
7
练习
1、计算
(1) (2) (3) (4)
(5) (6) (7) (8)
(-1)
7
(-1)
10
8
3
(-5)
3
0.1
3
1
2
—
(- )
4
(-10)4
(-10)5
1
2
—
(- )
4
解:
=1
=-1
=512
=-125
=0.001
1
16
= —
=10000
=-100000
3.判断下列各题是否正确:
( )① ;
( )② ;
( )③ ;
( )④ ;
对
错
错
错
4.计算:
先乘方、再乘除
运用新知 体会成功:
(1)、(-5)3 (2)、
(3)、5×23 (4)、(5×2)3
(5)、(-2)2 ×(-3)2
(6)、(-2)3÷ 22
-125
256
81
40
1000
36
-2
1.先乘方、再乘除、最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
2×(-3)3-4×(-3)+15
(-2)3+(-3)×[(-4)2+2]-(-3)2÷(-2)
例3 计算
解(1)第①行数是
-2,(-2)2 ,(-2)3 ,(-2)4 , …
(2)对比①②两行中位置对应的数,你有什么发现?第②行数是第①行相应的数加2,即
-2+2,(-2)2+2,(-2)3+2,(-2)4+2,…
例4 观察下面三行数:
-2,4,-8,16,-32,64,… ①
0,6,-6,18,-30,66,… ②
-1,2,-4,8,-16,32,… ③
(1)第①行数按什么规律排列
(2)第②③行数与第第①行数分别有什么关系?
(3)取每行数的第10个数,计算这三个数的和。
对比①③两行中位置对应的数,你有什么发现?第③行是第①行相应的数的0.5倍,即
-2X0.5,(-2)2X0.5,(-2)3X0.5,(-2)4X0.5,…
(3)每行数中的第10个数的和是
(-2)10+[(-2)10+2]+(-2)10X0.5
=1024+(1024+2)+1024X0.5
=1024+1026+512=2562
-2,4,-8,16,-32,64,… ①
0,6,-6,18,-30,66,… ②
-1,2,-4,8,-16,32,… ③
练习
计算:
(1)(-1)10×2+(-2)3÷4
(2)
思路:先算乘方,再算乘除,再算加减
解:原式=1×2+(-8)÷4
=2+(-2)=0
思路:先算乘方,再算乘法,再算减
思路:先算括号内的运算,再从左到右
解:原式=10000+(16-12X2)
=10000-8=9992
(4)(-10)4+[(-4)2-(3+32)X2]
(3)
有理数的混合运算法则
一般地,我们有:n个相同的因数a相乘,即a a … a,记作an
n个
幂
指数
底数
负数的奇次幂是负数
负数的偶次幂是正数
小结:
1.先乘方、再乘除、最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
3.若a为任意有理数,则a2一定是( )
A.正数 B.负数
C.非负数 D.非正数
B
C
结 束 寄 语
不经历风雨,怎能见彩虹!
下 课
