2.7有理数的乘法

(共30张PPT)
§2.7有理数的乘法
复习回顾：
计算下列各式：
（1）2＋2＋2＝_______；
（2）（－2）＋（－2）＋（－2）＝_______；
6
－6
①3+3+3+3=12，
②3+3+3+3=3×4=12.
几个相同加数的和的简便运算叫做乘法运算.
③（-3）+（-3）+（-3）+（-3）=-12
④（-3）+（-3）+（-3）+（-3）
=（-3）×4=-12
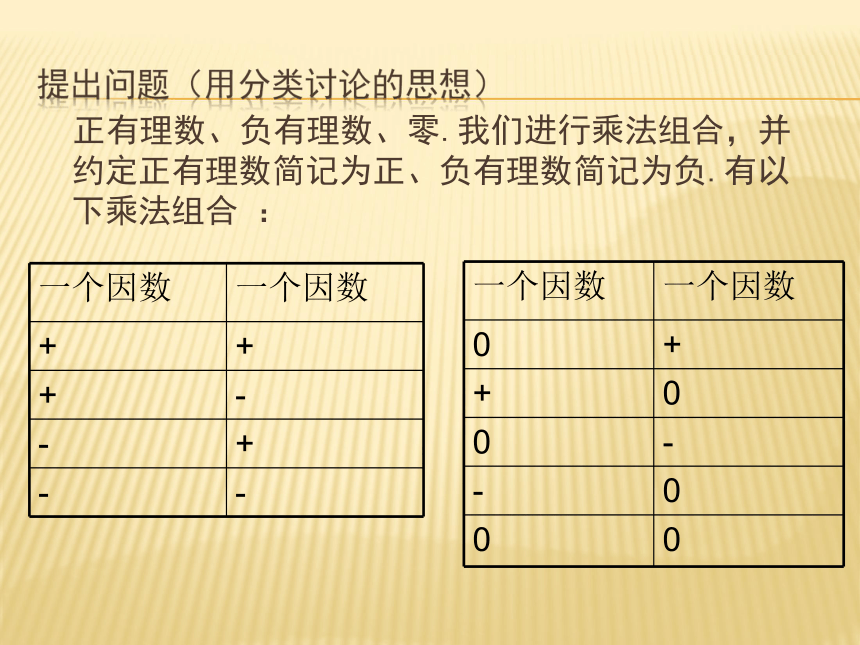
正有理数、负有理数、零.我们进行乘法组合，并约定正有理数简记为正、负有理数简记为负.有以下乘法组合 ：
一个因数 一个因数
0 +
+ 0
0 -
- 0
0 0
一个因数 一个因数
+ +
+ -
- +
- -
l
Ｏ
现规定：向左为负，向右为正;
时间以现在之前为负，现在之后为正．
探究1
l
l
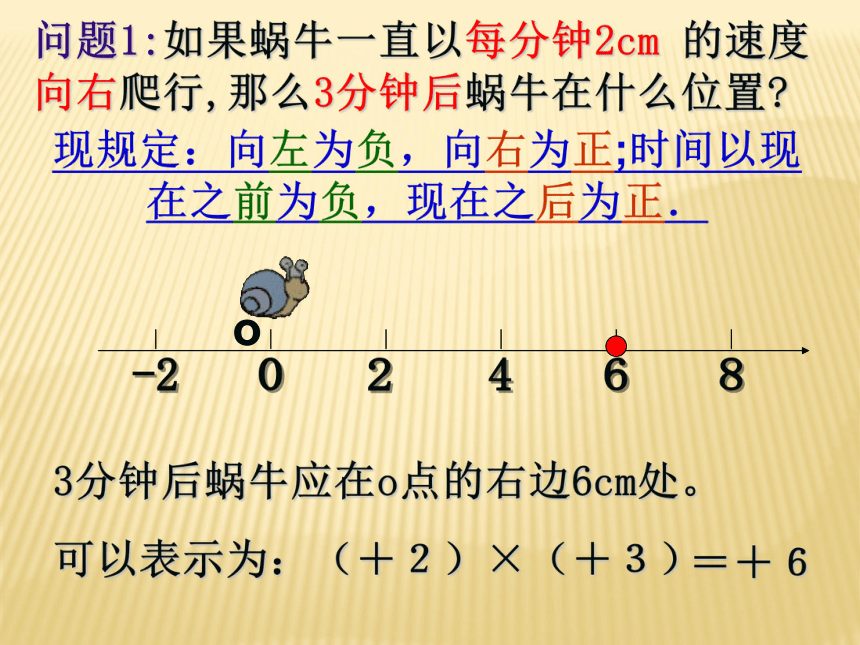
问题1:如果蜗牛一直以每分钟2cm 的速度向右爬行,那么3分钟后蜗牛在什么位置
3分钟后蜗牛应在o点的右边6cm处。
可以表示为：（＋２）×（＋３）
o
＝＋６
现规定：向左为负，向右为正;时间以现在之前为负，现在之后为正．
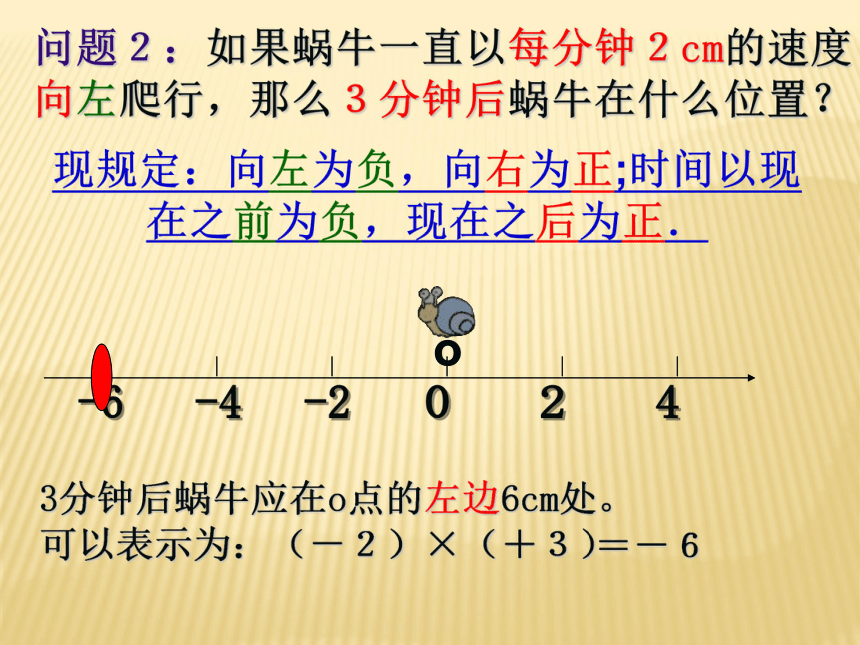
问题２：如果蜗牛一直以每分钟２cm的速度向左爬行，那么３分钟后蜗牛在什么位置？
3分钟后蜗牛应在o点的左边6cm处。
可以表示为：（－２）×（＋３）
o
＝－６
现规定：向左为负，向右为正;时间以现在之前为负，现在之后为正．
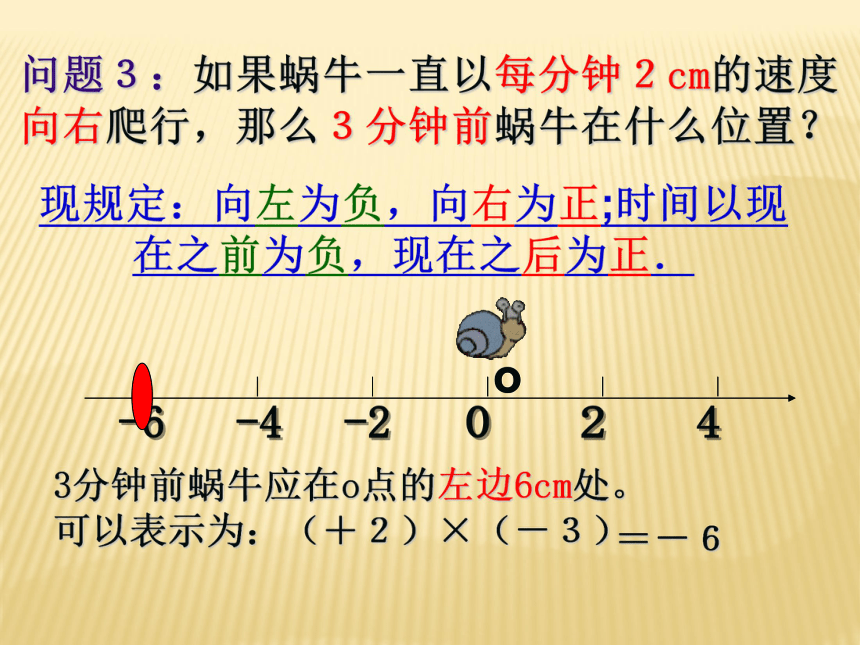
问题３：如果蜗牛一直以每分钟２cm的速度向右爬行，那么３分钟前蜗牛在什么位置？
3分钟前蜗牛应在o点的左边6cm处。
可以表示为：（＋２）×（－３）
o
＝－６
现规定：向左为负，向右为正;时间以现在之前为负，现在之后为正．
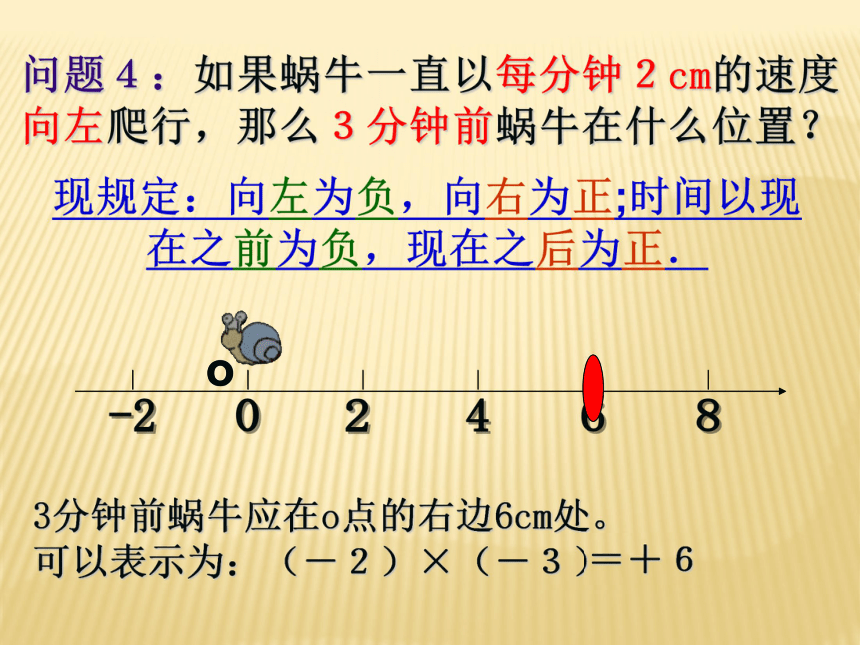
问题４：如果蜗牛一直以每分钟２cm的速度向左爬行，那么３分钟前蜗牛在什么位置？
3分钟前蜗牛应在o点的右边6cm处。
可以表示为：（－２）×（－３）
o
＝＋６
现规定：向左为负，向右为正;时间以现在之前为负，现在之后为正．
（5） 0 × 5 = 0
在原地运动5次
（-5）× 0 = 0
向左方运动0次
结果：被乘数是0或者乘数是0，结果仍为0。
0 × 0 = 0
观察这四个式子：
（＋２）×（＋３）＝＋６　
（－２）×（－３）＝＋６
（－２）×（＋３）＝－６　　
（＋２）×（－３）＝－６
根据你对有理数乘法的思考，总结填空：
正数乘正数积为＿数；负数乘负数积为＿数；
负数乘正数积为＿数；正数乘负数积为＿数；
乘积的绝对值等于各因数绝对值的＿＿。
正
正
负
负
积
(同号得正)
(异号得负)
两数相乘，同号得正,异号得负,
并把绝对值相乘。
任何数同０相乘，都得０。
两数的
符号特征 积的符号 积的绝对值
同 号
异 号
一个数
为0
有理数乘法法则:
+
-
绝对值相乘
绝对值相乘
得 0
先定符号,再定绝对值!
口答：确定下列两数积的符号。
（1） （－4） × （2） （－ ） ×（－9）
（3） 5×（－3） （4） 0.5×0.7
（5） （6）
=－（ ）
=+（ ）
=－（ ）
=+（ ）
=－（ ）
=－（ ）
例1 计算：
巩固练习：
1，计算：
计算步骤：先确定符号,再确定绝对值大小，与0相乘都得0；
2，口答：
20×(-2)=______
(-6)×(-9)=______
(-7)×(+8)=______
4×(-5)=______
(-7)×0=______
+(+5)=______
-(-5)=______
-40
54
-56
-20
0
5
+5
(+6)×（+5）=______
30
-(+5)=______
+(-5)=______
-5
-5
你发现两数相乘的积的符号的确定与数的符号化简有何联系？
3 计算：
在乘法计算时，遇到带分数，应先化为假分数；遇到小数，应先化成分数，再进行计算。
例2 用正负数表示气温的变化量，上升为正，下降为负。登山队攀登一座山峰，每登高1千米，气温的变化量为-6℃，攀登3千米后，气温有什么变化？
答：气温下降18℃。（气温上升-18 ℃ ）
解：（－6）×3=－（6×3）=－18（℃）
2，计算：
1
1
1
1
观察左边四组乘积，它们有什么共同点？
总结:有理数中仍然有:乘积是1的两个数
互为倒数.
数a(a≠0)的倒数是____；
3，写出下列各数的倒数：
注意：带分数或小数先化成假分数或分数，0没有倒数；
4，倒数等于它本身的数有_________;
±1
确定下列积的符号，试分析积的符号与各因数的符号之间有什么规律？
探索研究：
归纳：
当负因数的个数为奇数时，积为____;
当负因数的个数为偶数时，积为____。
结论1：几个不等于0的数相乘，积的符号由______________决定;
结论2：有一个因数为0，则积为____;
　
负因数的个数
负
正
0
1，判断下列积的符号
巩固练习
正
负
负
正
0
负
2，计算：
3、下列运算结果不一定为负数的是____
A.异号两数相乘 B.负数减去一个正数
C.异号两数相加 D.奇数个负因数的乘积
4若两个有理数的和与它们的积都是正数,则这两个数____
A.都是正数 B.是符号相同的非零数
C.都是负数 D.都是非负数
C
A
5如果a,b两数的和小于0，两数的积大于0，则a,b__________；
都小于0
6、下列运算错误的是_____
A.(-2)×(-3)=6 B.(-3)×(-2)×(-4)=-24
C.(-5)×(-2)×(-4)=-40 D.
7已知5个数的积为负数，则其中负因数的个数是_____
D
1或3或5
拓展练习：
(3)、数轴上点A、B、C、D分别对应有理数a,b,c,d ，
用“＞”“＝”“＜”填空：
(1)ac___0 (2)b-a____0
(3)a+b____0 (4)abcd___0
(5)(a+b)(c+d)____0 (6)(a-b)(c-d)____0
＞
＞
＞
＜
＜
＜
1、若ab>0,则必有（ ）
A、a>0 ,b>0 　 B、a<0, b<0
C、 a>0 ,b<0 　D、 a>0 ,b>0或a<0, b<0
2、若ab=0,则一定有（　）
A、a=b=0; B、a=0;
C、a、b至少有一个为０;　
D、 a、b至多有一个为０.
3 、若a+b>0,ab<0,则（　）
A、 a、b异号，且 　
B、 a、b异号，且a>b
C、 a、b异号，其中正数的绝对值大　
D、 a>0>b,或a<0D
C
C
　有理数乘法 　　　有理数加法
同号
异号
任何数与零
讨论对比
得正
得负
得零
得任何数
取相同的符号
　把绝对值相乘
（-2）×（-3）=6
　把绝对值相加
（-2）+（-3）=-5
取绝对值大的加数的符号
把绝对值相乘
（-2）×3= -6
（-2）+3=1
用较大的绝对值减小的绝对值
小结：
1.有理数乘法法则：
两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘,都得0。
2.求两个有理数的运算方法步骤：
先确定积的符号，再把绝对值相乘，当有一个因数为零时，积为零。
3、几个不等于0的数相乘，积的符号由负因数的个数决定; 当负因数的个数为奇数时，积为负;当负因数的个数为偶数时，积为正。