勾股定理电教课件

(共19张PPT)
在中国古代，人们把弯曲成直角的手臂的上半部分称为"勾"，下半部分称为"股"。
勾
股
图1-1
图1-2
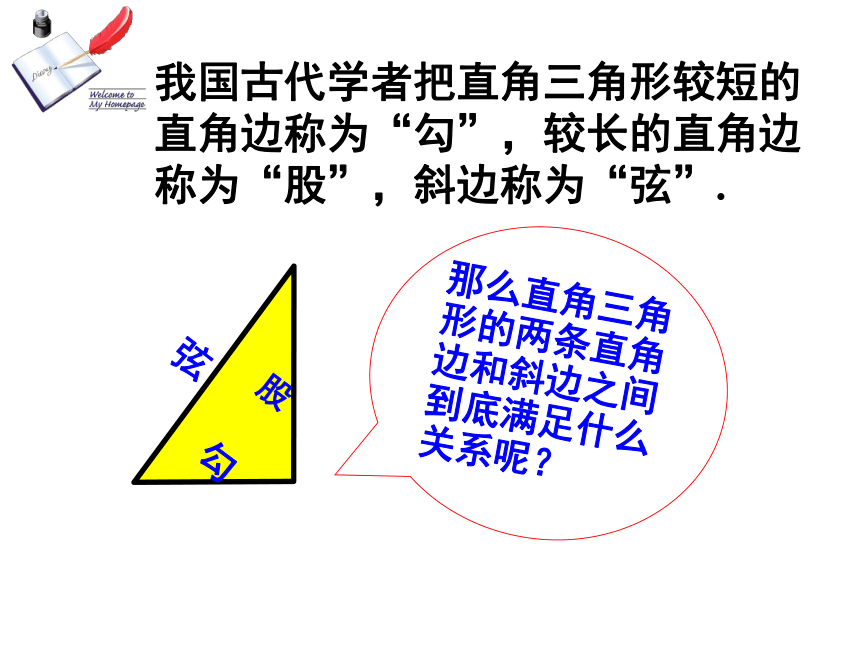
勾
股
弦
那么直角三角形的两条直角边和斜边之间到底满足什么关系呢？
我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.
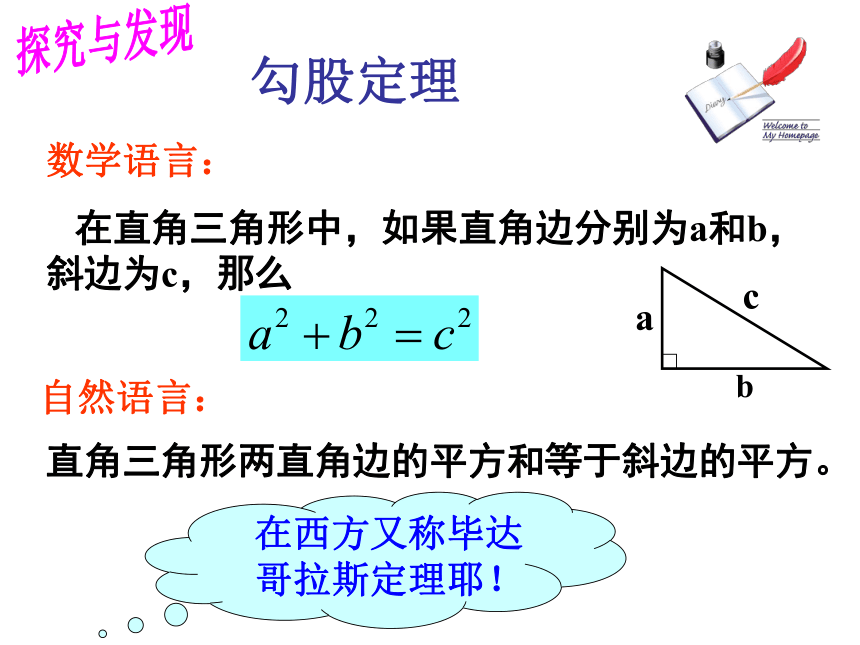
a2 + b2 = c2
b
a
c
a
a
b
b
c
Ⅰ
Ⅱ
Ⅲ
a
a
b
b
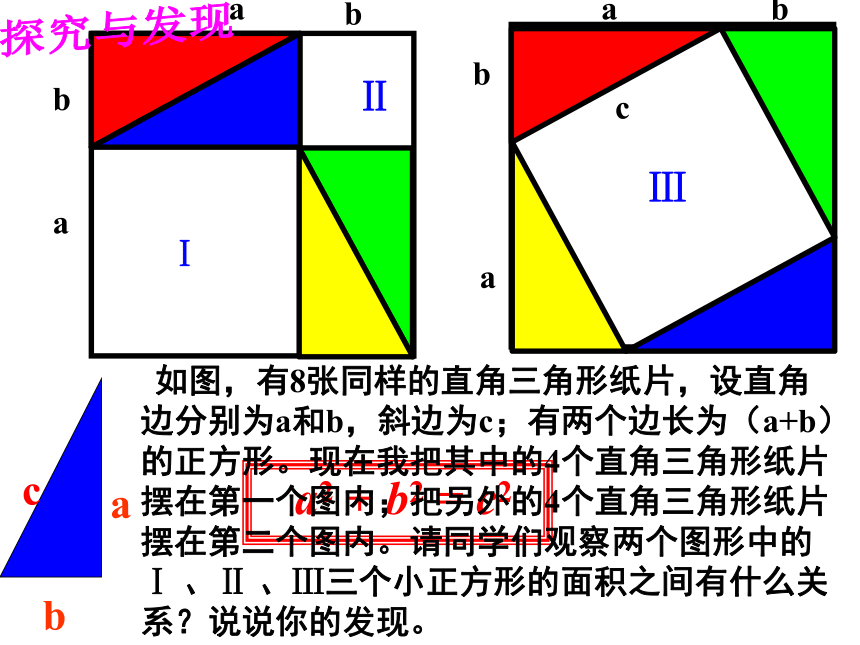
如图，有8张同样的直角三角形纸片，设直角边分别为a和b，斜边为c；有两个边长为（a+b）的正方形。现在我把其中的4个直角三角形纸片摆在第一个图内；把另外的4个直角三角形纸片摆在第二个图内。请同学们观察两个图形中的Ⅰ 、Ⅱ 、Ⅲ三个小正方形的面积之间有什么关系？说说你的发现。
Ⅰ
Ⅱ
勾股定理
直角三角形两直角边的平方和等于斜边的平方。
在直角三角形中，如果直角边分别为a和b，斜边为c，那么
数学语言：
自然语言：
a
b
c
在西方又称毕达哥拉斯定理耶！
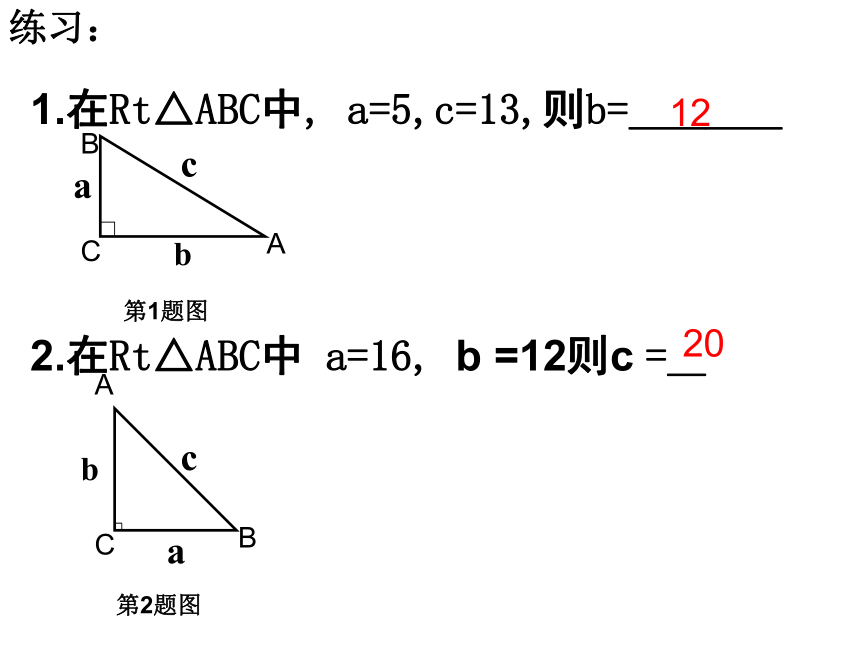
1.在Rt△ABC中, a=5,c=13,则b=＿＿＿＿
12
a
b
c
2.在Rt△ABC中 a=16, b =12则c =＿
a
b
c
第1题图
第2题图
练习：
C
B
A
C
B
A
20
y=0
练习：
3、在Rt△ABC中，斜边AB=1，则AB2+BC2+AC2= 。
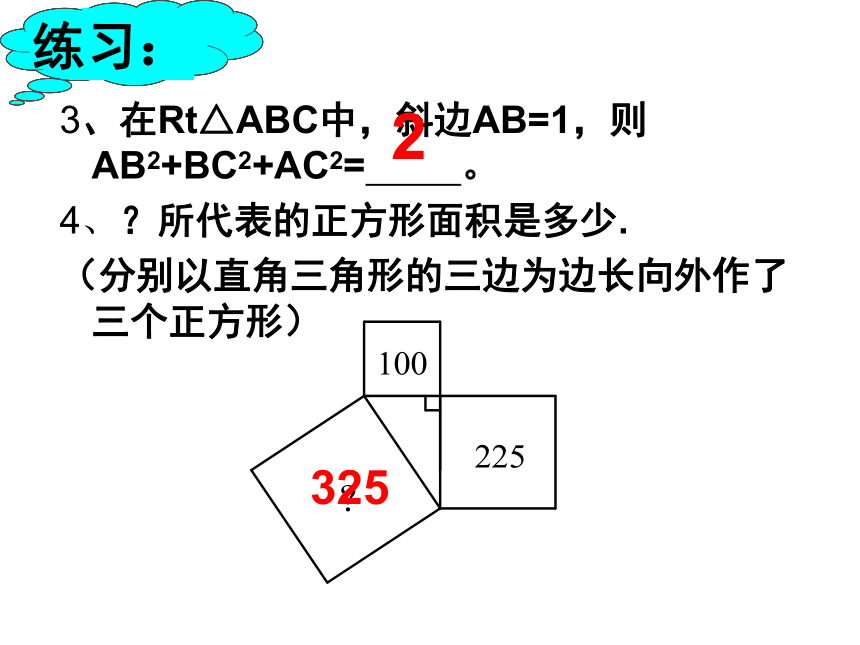
4、？所代表的正方形面积是多少.
（分别以直角三角形的三边为边长向外作了三个正方形）
2
325
勾股定理的应用
例1、如图，从电线杆OA的顶端A点，扯
一根钢丝绳固定在地面上的B点，这根钢
丝绳的长度是多少？
B
O
A
解
如图,在Rt△AOB中，∠O=90°,
AO=8米 ,BO=6米,
由勾股定理，得
AB2=AO2+BO2
=82+62=100
于是 AB= =10
所以，钢丝绳的长度为10米.
100
连接OB,OB与OA垂直,得直角三角形，在此直角三角形中，已知两直角边求斜边，应该用勾股定理.
分析：
8米
6米
索长有几？
明朝程大位的著作《算法统宗》里有一道“荡秋千”的趣题，是用诗歌的形式写的：
平地秋千未起，踏板一尺离地；
送行二步与人齐，五尺人高曾记。
仕女佳人争蹴，终朝笑语欢嬉；
良工高士好奇，算出索长有几？
例2、
现代汉语的意思是：
有一架秋千，当静止时其踏板离地1尺；将它向前推两步（一步为5尺）并使秋千的绳索拉直，其踏板离地5尺.求绳索的长
图1
有一架秋千，当静止时其踏板离地1尺；将它向前推两步（一步为5尺）并使秋千的绳索拉直，其踏板离地5尺.求绳索的长.
分析：画出如图的图形，由题意可知AC= ；CD= ;CF= .Rt OBF中设OB为x尺，你能解答这个题吗？
1尺
10尺
5尺
解：设绳索长为x尺，则OA=OB=x
AC=1，CF=5, BF=CD=10.
AF=CF-AC=5-1=4.
OF=OA-AF=x-4
在Rt△OBF中，由勾股定理得：
OB2=BF2+OF2,即
x2=102+(x-4)2
化简得：8x=116
解得：x=14.5
∴绳索长为14.5尺。
O
A
C
B
D
E
F
例2
a
a
b
b
c
c
∟
∟
∟
你能根据下图验证勾股定理吗？
y=0
总统证法
1) 在直角三角形中，两条直角边分别为a,b, 斜边为c，则c2=____
a2+b2
2) 在RT△ABC中∠C=90°,
⑴若a=4,b=3,则c=____
⑵若c=13,b=5,则a=____
5
12
达标检测
3) 在直角三角形中,如果有两边 为3,4,那么另一边为_________
5或 7
4：如图，一棵大树在一次强烈台风中于离地面5m断倒下，树顶落在离树根12m处.
大树在折断之前高多少？
5m
m
y=0
达标检测
12m
B
A
O
C
13m
两千多年前，古希腊有个哥拉
斯学派，他们首先发现了勾股定理，因此
在国外人们通常称勾股定理为毕达哥拉斯
定理。为了纪念毕达哥拉斯学派，1955
勾 股 世 界
国家之一。早在三千多年前，
国家之一。早在三千多年前，
国家之一。早在三千多年前，
国家之一。早在三千多年前，
国家之一。早在三千多年前，
两千多年前，古希腊有个毕达哥拉斯学派，他们首先发现了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯定理。
我国是最早了解勾股定理的国家之一。早在三千多年前，周朝数学家商高就提出 “勾三、股四、弦五”，它被记载于我国古代著名的数学著作《周髀算经》中。
勾股定理的历史
我国有记载的最早勾股定理的证明是三国时，我国古代数学家赵爽在他所著的《勾股圆方图注》中，用四个全等的直角三角形拼成一个中空的正方形来证明的。
这个图也叫弦图。
我国数学家华罗庚曾经建议，要探知其他星球上有没有“人”，我们可以发射左面的图形，如果他们是“文明人”，必定认识这种“语言”。
宇宙探索
课后延伸
1、解决问题：印度数学家拜斯达罗（公元1114～1185年）的著作中，有个有趣的“荷花问题”，是以诗歌的形式出现的：
湖静浪平六月天，荷花半尺出水面；
忽来一阵狂风急，吹倒花儿水中偃．
湖面之上不复见，入秋渔翁始发现；
残花离根二尺遥，试问水深尺若干？
2、通过查阅资料，了解勾股定理的文化背景。和它的更多证明方法。
3、 思考一下，知道三角形的三边长，你能否判断它是否为直角三角形？
心有多大，舞台就有多大！
同学们，放飞你们的思想，努力学习吧！