2021-2022学年京改版数学九年级上册19.1二次函数同步训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年京改版数学九年级上册19.1二次函数同步训练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 240.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 10:00:43 | ||
图片预览



文档简介
19.1二次函数——同步训练
一、单选题(共15题)
1.抛物线y=x,y=﹣2019x+2020,y=2019x共有的性质是( )
A.开口向上 B.都有最低点
C.当x>0时,y随x的增大而增大 D.对称轴是y轴
2.若二次函数y=的图像经过A(-1,a),B(2,b),C(4.5,c)三点,则a、b、c 的大小关系是( )
A. B. C. D.
3.抛物线的顶点坐标为( )
A. B. C. D.
4.已知二次函数y=﹣x2+2x﹣3,用配方法化为y=a(x﹣h)2+k的形式,结果是( )
A.y=﹣(x﹣1)2﹣2 B.y=﹣(x﹣1)2+2 C.y=﹣(x﹣1)2+4 D.y=﹣(x+1)2﹣4
5.抛物线的顶点为,与轴的一个交点在点和之间,其部分图象如图所示,则以下结论:①;②;③;④方程以有两个的实根,其中正确的个数为( )
A.1 B.2 C.3 D.4
6.若点A(-,y1),B(-1,y2),C (,y3)为二次函数y=-x2-4x+m的图象上的三个点,则y1,y2,y3的大小关系为( )
A.y2>y1>y3 B.y1>y3>y2 C.y3>y2>y1 D.y2>y3>y1
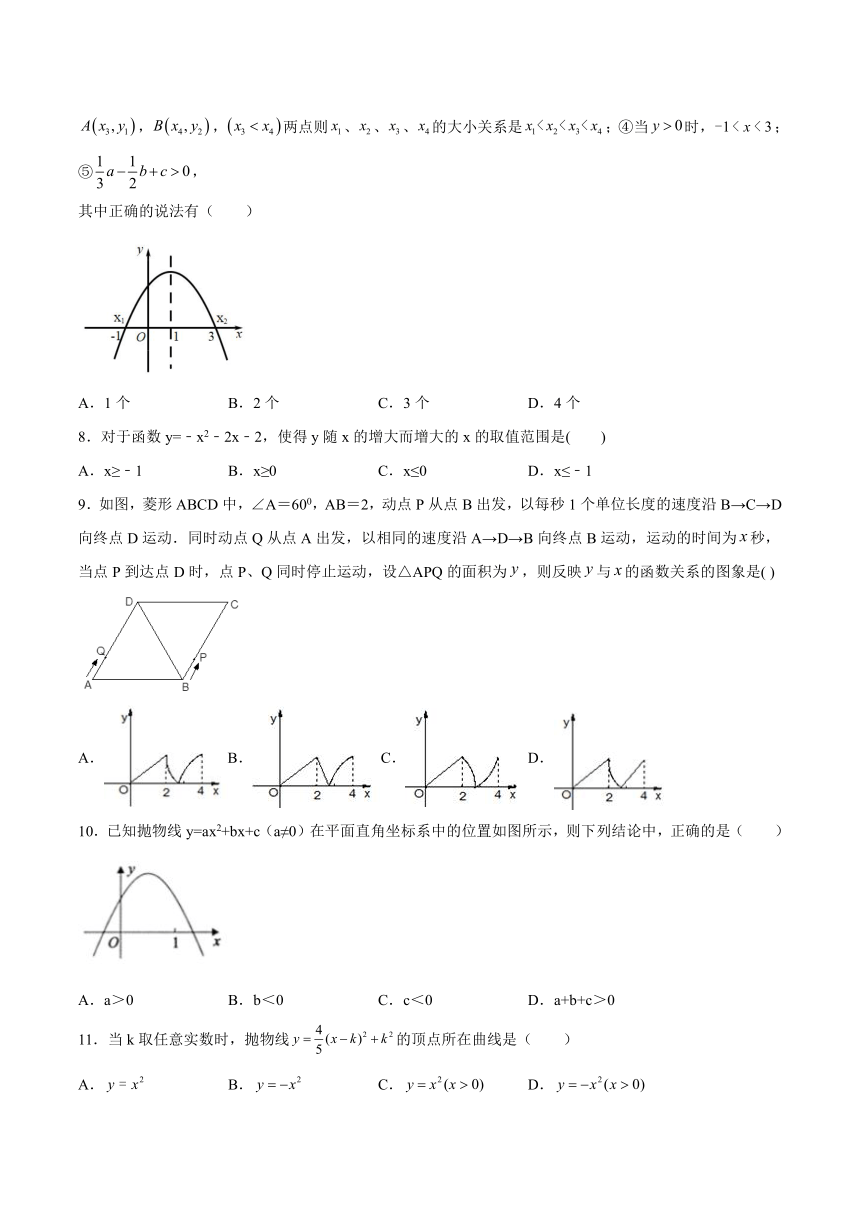
7.二次函数的图象如图所示,给出下列说法:
①;②方程的根为、;③若直线与的图象相交于,,两点则、、、的大小关系是;④当时,;⑤,
其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
8.对于函数y=﹣x2﹣2x﹣2,使得y随x的增大而增大的x的取值范围是( )
A.x≥﹣1 B.x≥0 C.x≤0 D.x≤﹣1
9.如图,菱形ABCD中,∠A=600,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为,则反映与的函数关系的图象是( )
A.B.C. D.
10.已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中,正确的是( )
A.a>0 B.b<0 C.c<0 D.a+b+c>0
11.当k取任意实数时,抛物线的顶点所在曲线是( )
A. B. C. D.
12.如图,函数的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),
对称轴是x =-1.在下列结论中,错误的是( )
A.顶点坐标为(-1,4) B.函数的解析式为
C.当时,y随x的增大而增大 D.抛物线与x轴的另一个交点是(-3,0)
13.若抛物线y=x2﹣2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位,再沿铅直方向向上平移三个单位,则原抛物线图象的解析式应变为( )
A.y=(x﹣2)2+3 B.y=(x﹣2)2+5 C.y=x2﹣1 D.y=x2+4
14.如图,二次函数的图象经过点,下列说法正确的是( )
A. B. C. D.图象的对称轴是直线
15.如图为某菜农搭建的一个横截面为抛物线的大棚,有关尺寸如图所示,某菜农身高1.6米,则他在不弯腰的情况下在大棚内左右活动的范围是( )
A.米 B.米 C.1.6米 D.0.8米
二、填空题(共6题)
16.抛物线与抛物线的关系:
向____(h>0)或向_____(h<0)平移|h|个单位长度,再向____(h>0)或向____(h<0)平移|k|个单位长度,得到
17.若用长的篱笆围成长方形的生物园来饲养动物,则生物园的最大面积为_______.
18.函数的图象是__________,对称轴是__________,顶点是__________;当x__________时,y随x的增大而增大;当x__________时,y随x的增大而减小;当__________时,y有最__________值.
19.如图所示,二次函数的图像与轴交于点,对称轴为直线.则方程的两个根为_____.
20.抛物线与x轴的正半轴交于A、B两点,与y轴交于C点,且线段AB的长为1,△ABC的面积为1,则b的值为_____________
21.如图,在平面直角坐标系中,过点P(m,0)作x轴的垂线,分别交抛物线y=x2+2与直线y=﹣x于A、B,以线段AB为对角线作正方形ACBD,则正方形ACBD的面积的最小值为_____.
三、解答题(共4题)
22.如图所示,在矩形ABCD中,AB=6厘米,BC=12厘米,点P在线段AB上,P从点A开始沿AB边以1厘米/秒的速度向点B移动.点E为线段BC的中点,点Q从E点开始,沿EC以1厘米/秒的速度向点C移动.如果P、Q同时分别从A、E出发,写出出发时间t与△BPQ的面积S的函数关系式,求出t的取值范围.
23.某超市3月份购进一批牛肉销售,比去年同期进价降16元/千克,去年3月份购买80千克的牛肉的钱,今年3月份可以购买100千克的牛肉.
(1)今年3月份购进这批牛肉每千克多少元?
(2)若今年3月份该超市购进牛肉后每天的牛肉销售量(千克)与销售单价(元/千克)满足如图所示的一次函数关系.求与之间的函数关系式;
(3)这批牛肉的销售单价定为x元/千克,每天的所有其他成本共计为200元/天,且66≤x≤80,求今年3月份该超市销售牛肉每天利润的取值范围?(利润=销售收入-进货金额-其他成本)
24.函数图象在探索函数的性质中有非常重要的作用,如图一是函数y=x2﹣1的图象,通过图象可以探究它的对称性,增减性,最值等情况.下面对函数y=|x2﹣1|展开探索.经历分析解析式、列表、描点、连线等过程得到函数y=|x2﹣1|的图象如图二所示:
x … ﹣3 ﹣ ﹣2 ﹣ ﹣1 ﹣ 0 1 2 3 …
y … 8 3 a 0 1 b 0 3 8 …
(1)表格中a= ,b= ;
(2)观察发现:函数y=|x2﹣1|的图象是轴对称图形,写出该函数图象的对称轴;
(3)拓展应用:①如果y随x的增大而增大,则x的取值范围是 ;
②已知方程|x2﹣1|=k(k是一个常数)有两个解,则k的取值范围是 .
25.已知抛物线的最高点为P(3,4),且经过点A(0,1),求的解析式。
参考答案
1.D2.D3.C4.A5.B6.A7.D8.D9.A10.D11.A12.C13.C14.D15.B
16.右 左 上 下
17.16m2
18.抛物线 y轴(或直线) 0 小
19.,
20.-3.
21.
22.S=﹣t2+18(0≤t<6)
23.(1)64元;(2)y=-10x+840;(3)160≤w≤800.
24.(1)a=,b=;(2)x=0;(3)①x>1或﹣1<x<0;②k>1或k=0.
25.
一、单选题(共15题)
1.抛物线y=x,y=﹣2019x+2020,y=2019x共有的性质是( )
A.开口向上 B.都有最低点
C.当x>0时,y随x的增大而增大 D.对称轴是y轴
2.若二次函数y=的图像经过A(-1,a),B(2,b),C(4.5,c)三点,则a、b、c 的大小关系是( )
A. B. C. D.
3.抛物线的顶点坐标为( )
A. B. C. D.
4.已知二次函数y=﹣x2+2x﹣3,用配方法化为y=a(x﹣h)2+k的形式,结果是( )
A.y=﹣(x﹣1)2﹣2 B.y=﹣(x﹣1)2+2 C.y=﹣(x﹣1)2+4 D.y=﹣(x+1)2﹣4
5.抛物线的顶点为,与轴的一个交点在点和之间,其部分图象如图所示,则以下结论:①;②;③;④方程以有两个的实根,其中正确的个数为( )
A.1 B.2 C.3 D.4
6.若点A(-,y1),B(-1,y2),C (,y3)为二次函数y=-x2-4x+m的图象上的三个点,则y1,y2,y3的大小关系为( )
A.y2>y1>y3 B.y1>y3>y2 C.y3>y2>y1 D.y2>y3>y1
7.二次函数的图象如图所示,给出下列说法:
①;②方程的根为、;③若直线与的图象相交于,,两点则、、、的大小关系是;④当时,;⑤,
其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
8.对于函数y=﹣x2﹣2x﹣2,使得y随x的增大而增大的x的取值范围是( )
A.x≥﹣1 B.x≥0 C.x≤0 D.x≤﹣1
9.如图,菱形ABCD中,∠A=600,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为,则反映与的函数关系的图象是( )
A.B.C. D.
10.已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中,正确的是( )
A.a>0 B.b<0 C.c<0 D.a+b+c>0
11.当k取任意实数时,抛物线的顶点所在曲线是( )
A. B. C. D.
12.如图,函数的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),
对称轴是x =-1.在下列结论中,错误的是( )
A.顶点坐标为(-1,4) B.函数的解析式为
C.当时,y随x的增大而增大 D.抛物线与x轴的另一个交点是(-3,0)
13.若抛物线y=x2﹣2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位,再沿铅直方向向上平移三个单位,则原抛物线图象的解析式应变为( )
A.y=(x﹣2)2+3 B.y=(x﹣2)2+5 C.y=x2﹣1 D.y=x2+4
14.如图,二次函数的图象经过点,下列说法正确的是( )
A. B. C. D.图象的对称轴是直线
15.如图为某菜农搭建的一个横截面为抛物线的大棚,有关尺寸如图所示,某菜农身高1.6米,则他在不弯腰的情况下在大棚内左右活动的范围是( )
A.米 B.米 C.1.6米 D.0.8米
二、填空题(共6题)
16.抛物线与抛物线的关系:
向____(h>0)或向_____(h<0)平移|h|个单位长度,再向____(h>0)或向____(h<0)平移|k|个单位长度,得到
17.若用长的篱笆围成长方形的生物园来饲养动物,则生物园的最大面积为_______.
18.函数的图象是__________,对称轴是__________,顶点是__________;当x__________时,y随x的增大而增大;当x__________时,y随x的增大而减小;当__________时,y有最__________值.
19.如图所示,二次函数的图像与轴交于点,对称轴为直线.则方程的两个根为_____.
20.抛物线与x轴的正半轴交于A、B两点,与y轴交于C点,且线段AB的长为1,△ABC的面积为1,则b的值为_____________
21.如图,在平面直角坐标系中,过点P(m,0)作x轴的垂线,分别交抛物线y=x2+2与直线y=﹣x于A、B,以线段AB为对角线作正方形ACBD,则正方形ACBD的面积的最小值为_____.
三、解答题(共4题)
22.如图所示,在矩形ABCD中,AB=6厘米,BC=12厘米,点P在线段AB上,P从点A开始沿AB边以1厘米/秒的速度向点B移动.点E为线段BC的中点,点Q从E点开始,沿EC以1厘米/秒的速度向点C移动.如果P、Q同时分别从A、E出发,写出出发时间t与△BPQ的面积S的函数关系式,求出t的取值范围.
23.某超市3月份购进一批牛肉销售,比去年同期进价降16元/千克,去年3月份购买80千克的牛肉的钱,今年3月份可以购买100千克的牛肉.
(1)今年3月份购进这批牛肉每千克多少元?
(2)若今年3月份该超市购进牛肉后每天的牛肉销售量(千克)与销售单价(元/千克)满足如图所示的一次函数关系.求与之间的函数关系式;
(3)这批牛肉的销售单价定为x元/千克,每天的所有其他成本共计为200元/天,且66≤x≤80,求今年3月份该超市销售牛肉每天利润的取值范围?(利润=销售收入-进货金额-其他成本)
24.函数图象在探索函数的性质中有非常重要的作用,如图一是函数y=x2﹣1的图象,通过图象可以探究它的对称性,增减性,最值等情况.下面对函数y=|x2﹣1|展开探索.经历分析解析式、列表、描点、连线等过程得到函数y=|x2﹣1|的图象如图二所示:
x … ﹣3 ﹣ ﹣2 ﹣ ﹣1 ﹣ 0 1 2 3 …
y … 8 3 a 0 1 b 0 3 8 …
(1)表格中a= ,b= ;
(2)观察发现:函数y=|x2﹣1|的图象是轴对称图形,写出该函数图象的对称轴;
(3)拓展应用:①如果y随x的增大而增大,则x的取值范围是 ;
②已知方程|x2﹣1|=k(k是一个常数)有两个解,则k的取值范围是 .
25.已知抛物线的最高点为P(3,4),且经过点A(0,1),求的解析式。
参考答案
1.D2.D3.C4.A5.B6.A7.D8.D9.A10.D11.A12.C13.C14.D15.B
16.右 左 上 下
17.16m2
18.抛物线 y轴(或直线) 0 小
19.,
20.-3.
21.
22.S=﹣t2+18(0≤t<6)
23.(1)64元;(2)y=-10x+840;(3)160≤w≤800.
24.(1)a=,b=;(2)x=0;(3)①x>1或﹣1<x<0;②k>1或k=0.
25.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
