2021-2022学年京改版数学九年级上册19.2反比例函数同步训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年京改版数学九年级上册19.2反比例函数同步训练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 342.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 09:59:19 | ||
图片预览

文档简介
19.2反比例函数——同步训练
一、单选题(共15题)
1.对于每一象限内的双曲线,都随的增大而增大,则的取值范围是( )
A. B. C. D.
2.下列选项中,y是x的反比例函数的是( )
A. B. C. D.
3.若反比例函数的图象经过第二、四象限,则为( )
A.1 B.-1 C.±1 D.
4.若点、、都在反比例函数的图象,则下列各式中正确的是( )
A. B. C. D.
5.已知正比例函数y1=kx与反比例函数y2=- (k≠0),则下列说法正确的是( )
A.当k>0时,正比例函数y1随x的增大而减小
B.当x>0时,y1C.两个函数的图象的交点关于原点对称
D.当k>0时,在第四象限内,反比例函数y2随x的增大而增大
6.某药品研究所开发一种抗新冠肺炎的新药,经大量动物实验,首次用于临床人体实验,测得成人服药后血液中药物浓度(微克/毫升)与服药时间小时之间的函数关系如图所示(当时,与成反比),若血液中药物浓度不低于4微克/毫升的持续时间不低于6.5小时,则称药物治疗有效.根据图象信息计算并判断下列选项错误的是( )
A.当血液中药物浓度上升时,与之间的函数关系式是.
B.当血液中药物浓度下降时,与之间的函数关系式是.
C.血液中药物浓度不低于4微克/毫升的持续时间为5个小时.
D.这种抗菌新药不可以作为有效药物投入生产.
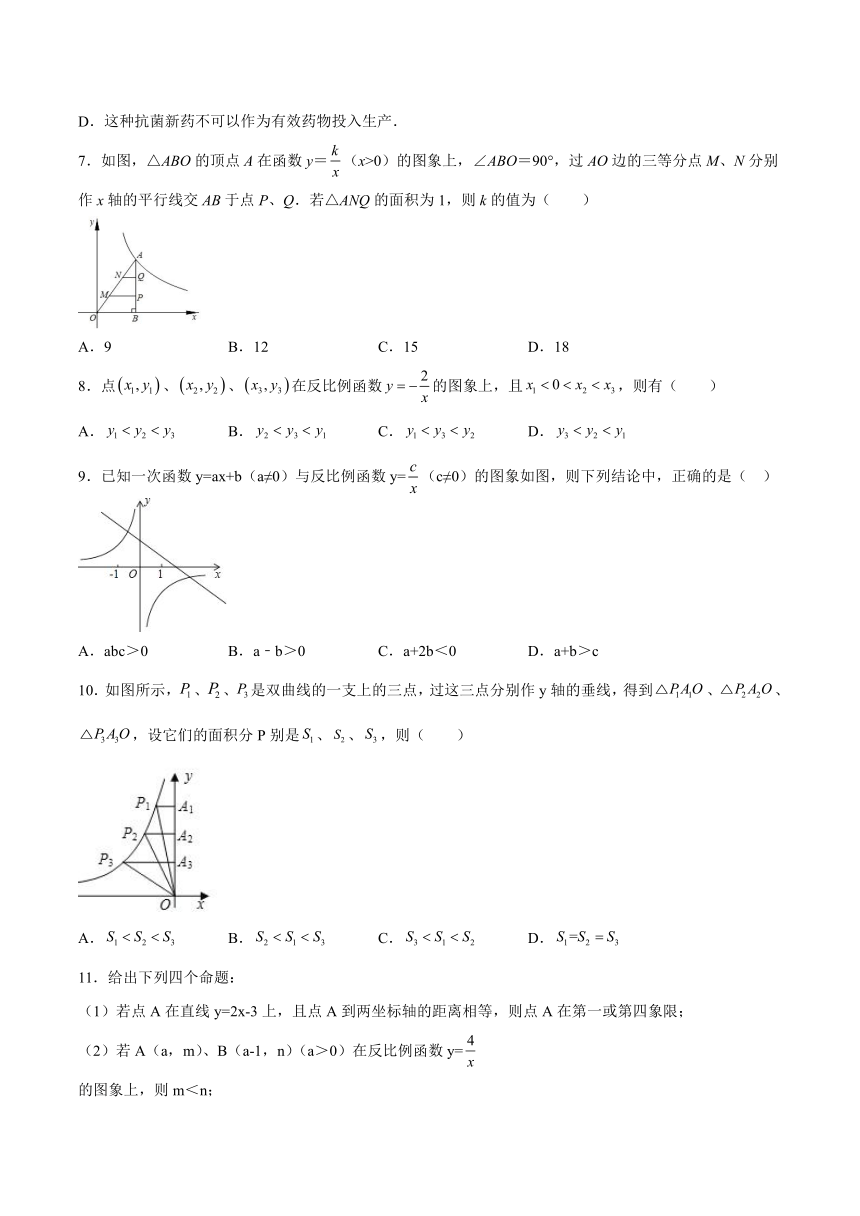
7.如图,△ABO的顶点A在函数y=(x>0)的图象上,∠ABO=90°,过AO边的三等分点M、N分别作x轴的平行线交AB于点P、Q.若△ANQ的面积为1,则k的值为( )
A.9 B.12 C.15 D.18
8.点、、在反比例函数的图象上,且,则有( )
A. B. C. D.
9.已知一次函数y=ax+b(a≠0)与反比例函数y=(c≠0)的图象如图,则下列结论中,正确的是( )
A.abc>0 B.a﹣b>0 C.a+2b<0 D.a+b>c
10.如图所示,、、是双曲线的一支上的三点,过这三点分别作y轴的垂线,得到、、,设它们的面积分P别是、、,则( )
A. B. C. D.
11.给出下列四个命题:
(1)若点A在直线y=2x-3上,且点A到两坐标轴的距离相等,则点A在第一或第四象限;
(2)若A(a,m)、B(a-1,n)(a>0)在反比例函数y=
的图象上,则m<n;
(3)一次函数y=-2x-3的图象不经过第三象限;
(4)二次函数y=-2x2-8x+1的最大值是9.
正确命题的个数是( )
A.1个 B.2个 C.3个 D.4个
12.函数与在同一坐标系中的大致图象是( )
A. B. C. D.
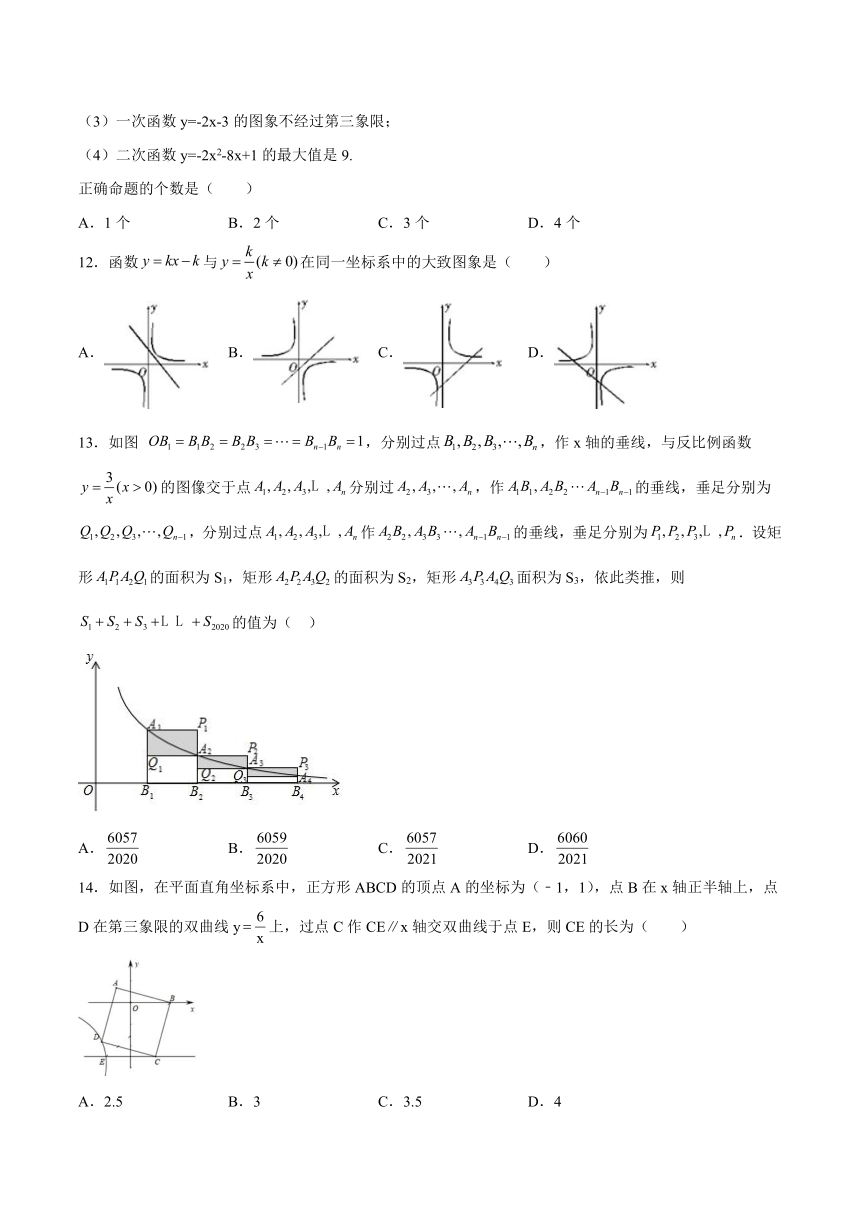
13.如图 ,分别过点,作x轴的垂线,与反比例函数的图像交于点分别过,作的垂线,垂足分别为,分别过点作的垂线,垂足分别为.设矩形的面积为S1,矩形的面积为S2,矩形面积为S3,依此类推,则的值为( )
A. B. C. D.
14.如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(﹣1,1),点B在x轴正半轴上,点D在第三象限的双曲线y上,过点C作CE∥x轴交双曲线于点E,则CE的长为( )
A.2.5 B.3 C.3.5 D.4
15.如图,直线AB交反比例函数于P,Q两点,点A,B分别在x轴,y轴上,连接OQ,恰有OQ⊥AB,连接OP,若OP:QA=:1,△OPQ的面积为12,则k的值为( )
A. B. C. D.
二、填空题(共6题)
16.写一个反比例函数的解析式,使它的图象在第一、三象限:_____.
17.如图,平行四边形ABCD的顶点为A、C在双曲线上,B、D在双曲线上,k1=2k2(k1>0),AB∥y轴,S△ABCD=24,则k1=_____.
18.写出图象经过点(﹣1,1)的一个函数的解析式是 .
19.反比例函数的图象过点(﹣2,﹣3),则此函数的解析式是_______.
20.如图,直线与双曲线交于点,,点是直线上一动点,且点在第二象限.连接并延长交双曲线于点.过点作轴,垂足为点.过点作轴,垂足为.若点的坐标为,点的坐标为,设的面积为,的面积为,当时,点的横坐标的取值范围为______.
21.如图,在 x 轴上取 OB1=B1B2=B2B3=…=a,过 B1、B2、B3…分别作 x 轴的垂线,交反比例函数y= (x>0)的图象于 A1、A2 、A3 …,连接 OA1、B1A2、B2 A3 …,则 S△A n B n B n-1=_____.
三、解答题(共4题)
22.如图,在平面直角坐标系中,反比例函数的图象经过点A(1, 2),B(m ,n)(m>1),过点B作y轴的垂线,垂足为C.
(1)求该反比例函数解析式;
(2)当△ABC面积为2时,求点B的坐标
23.如图,在平面直角坐标系中,直线l经过原点,且与反比例函数图象 y=交于点 A(1,2),点B(m,-2).分别过A,B作AC⊥y轴于C,BD⊥y轴于D,再以AC,BD为半径作⊙A和⊙B.
(1)求反比例函数的解析式及m的值;
(2)求图中阴影部分的面积.
24.已知质量一定的某物体的体积V(m3)是密度ρ(kg/m3)的反比例函数,其图象如图所示:
(1)请写出该物体的体积V与密度ρ的函数关系式;
(2)当该物体的密度ρ=3.2Kg/m3时,它的体积v是多少?
(3)如果将该物体的体积控制在10m3~40m3之间,那么该物体的密度应在什么范围内变化?
25.如图,一次函数的图象与反比例函数的图象相交于点A(2,3)
和点B,与轴相交于点C(8,0) .
(1)求这两个函数的解析式;
(2)当取何值时,.
参考答案
1.B2.C3.B4.C5.D6.C7.D8.B9.A10.D11.B12.C13.D14.C
15.A
16.
17.8.
18.y=﹣x
19..
20.-6<x<-2
21.
22.(1),(2)(3,)
23.(1)y=, m=-1;(2)π.
24.(1)V=;(2)10(m)3;(3)该物体的密度在0.8Kg/m3~3.2Kg/m3的范围内变化.
25.(1)=x+4,=.
(2)当x<0或2<x<6时,
一、单选题(共15题)
1.对于每一象限内的双曲线,都随的增大而增大,则的取值范围是( )
A. B. C. D.
2.下列选项中,y是x的反比例函数的是( )
A. B. C. D.
3.若反比例函数的图象经过第二、四象限,则为( )
A.1 B.-1 C.±1 D.
4.若点、、都在反比例函数的图象,则下列各式中正确的是( )
A. B. C. D.
5.已知正比例函数y1=kx与反比例函数y2=- (k≠0),则下列说法正确的是( )
A.当k>0时,正比例函数y1随x的增大而减小
B.当x>0时,y1
D.当k>0时,在第四象限内,反比例函数y2随x的增大而增大
6.某药品研究所开发一种抗新冠肺炎的新药,经大量动物实验,首次用于临床人体实验,测得成人服药后血液中药物浓度(微克/毫升)与服药时间小时之间的函数关系如图所示(当时,与成反比),若血液中药物浓度不低于4微克/毫升的持续时间不低于6.5小时,则称药物治疗有效.根据图象信息计算并判断下列选项错误的是( )
A.当血液中药物浓度上升时,与之间的函数关系式是.
B.当血液中药物浓度下降时,与之间的函数关系式是.
C.血液中药物浓度不低于4微克/毫升的持续时间为5个小时.
D.这种抗菌新药不可以作为有效药物投入生产.
7.如图,△ABO的顶点A在函数y=(x>0)的图象上,∠ABO=90°,过AO边的三等分点M、N分别作x轴的平行线交AB于点P、Q.若△ANQ的面积为1,则k的值为( )
A.9 B.12 C.15 D.18
8.点、、在反比例函数的图象上,且,则有( )
A. B. C. D.
9.已知一次函数y=ax+b(a≠0)与反比例函数y=(c≠0)的图象如图,则下列结论中,正确的是( )
A.abc>0 B.a﹣b>0 C.a+2b<0 D.a+b>c
10.如图所示,、、是双曲线的一支上的三点,过这三点分别作y轴的垂线,得到、、,设它们的面积分P别是、、,则( )
A. B. C. D.
11.给出下列四个命题:
(1)若点A在直线y=2x-3上,且点A到两坐标轴的距离相等,则点A在第一或第四象限;
(2)若A(a,m)、B(a-1,n)(a>0)在反比例函数y=
的图象上,则m<n;
(3)一次函数y=-2x-3的图象不经过第三象限;
(4)二次函数y=-2x2-8x+1的最大值是9.
正确命题的个数是( )
A.1个 B.2个 C.3个 D.4个
12.函数与在同一坐标系中的大致图象是( )
A. B. C. D.
13.如图 ,分别过点,作x轴的垂线,与反比例函数的图像交于点分别过,作的垂线,垂足分别为,分别过点作的垂线,垂足分别为.设矩形的面积为S1,矩形的面积为S2,矩形面积为S3,依此类推,则的值为( )
A. B. C. D.
14.如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(﹣1,1),点B在x轴正半轴上,点D在第三象限的双曲线y上,过点C作CE∥x轴交双曲线于点E,则CE的长为( )
A.2.5 B.3 C.3.5 D.4
15.如图,直线AB交反比例函数于P,Q两点,点A,B分别在x轴,y轴上,连接OQ,恰有OQ⊥AB,连接OP,若OP:QA=:1,△OPQ的面积为12,则k的值为( )
A. B. C. D.
二、填空题(共6题)
16.写一个反比例函数的解析式,使它的图象在第一、三象限:_____.
17.如图,平行四边形ABCD的顶点为A、C在双曲线上,B、D在双曲线上,k1=2k2(k1>0),AB∥y轴,S△ABCD=24,则k1=_____.
18.写出图象经过点(﹣1,1)的一个函数的解析式是 .
19.反比例函数的图象过点(﹣2,﹣3),则此函数的解析式是_______.
20.如图,直线与双曲线交于点,,点是直线上一动点,且点在第二象限.连接并延长交双曲线于点.过点作轴,垂足为点.过点作轴,垂足为.若点的坐标为,点的坐标为,设的面积为,的面积为,当时,点的横坐标的取值范围为______.
21.如图,在 x 轴上取 OB1=B1B2=B2B3=…=a,过 B1、B2、B3…分别作 x 轴的垂线,交反比例函数y= (x>0)的图象于 A1、A2 、A3 …,连接 OA1、B1A2、B2 A3 …,则 S△A n B n B n-1=_____.
三、解答题(共4题)
22.如图,在平面直角坐标系中,反比例函数的图象经过点A(1, 2),B(m ,n)(m>1),过点B作y轴的垂线,垂足为C.
(1)求该反比例函数解析式;
(2)当△ABC面积为2时,求点B的坐标
23.如图,在平面直角坐标系中,直线l经过原点,且与反比例函数图象 y=交于点 A(1,2),点B(m,-2).分别过A,B作AC⊥y轴于C,BD⊥y轴于D,再以AC,BD为半径作⊙A和⊙B.
(1)求反比例函数的解析式及m的值;
(2)求图中阴影部分的面积.
24.已知质量一定的某物体的体积V(m3)是密度ρ(kg/m3)的反比例函数,其图象如图所示:
(1)请写出该物体的体积V与密度ρ的函数关系式;
(2)当该物体的密度ρ=3.2Kg/m3时,它的体积v是多少?
(3)如果将该物体的体积控制在10m3~40m3之间,那么该物体的密度应在什么范围内变化?
25.如图,一次函数的图象与反比例函数的图象相交于点A(2,3)
和点B,与轴相交于点C(8,0) .
(1)求这两个函数的解析式;
(2)当取何值时,.
参考答案
1.B2.C3.B4.C5.D6.C7.D8.B9.A10.D11.B12.C13.D14.C
15.A
16.
17.8.
18.y=﹣x
19..
20.-6<x<-2
21.
22.(1),(2)(3,)
23.(1)y=, m=-1;(2)π.
24.(1)V=;(2)10(m)3;(3)该物体的密度在0.8Kg/m3~3.2Kg/m3的范围内变化.
25.(1)=x+4,=.
(2)当x<0或2<x<6时,
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
