2021-2022学年人教版八年级数学上册14.2乘法公式 同步达标测试 (word版含解析)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册14.2乘法公式 同步达标测试 (word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 134.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 11:54:13 | ||
图片预览



文档简介
2021-2022学年人教版八年级数学上册《14.2乘法公式》同步达标测试(附答案)
一.选择题(共8小题,满分40分)
1.若x2+mx+k是一个完全平方式,则k等于( )
A. B. C. D.m2
2.下列运算中,正确的是( )
A.(a﹣2)2=a2﹣4 B.(a+3)2=a2+9
C.(a﹣1)(a﹣2)=a2﹣3a+2 D.(a﹣2)(2﹣a)=a2﹣4
3.当n为正整数时,代数式(2n+1)2﹣(2n﹣1)2一定是下面哪个数的倍数( )
A.3 B.5 C.7 D.8
4.若a+b=6,a2﹣b2=30,则a﹣b=( )
A.5 B.6 C.10 D.15
5.(3+2)×(32+22)×(34+24)×(38+28)计算结果等于( )
A.1 B.316﹣216 C.332+232 D.332﹣232
6.如图1,在边长为a的正方形中剪去一个边长为b(b<a)的小正方形,把剩下部分拼成一个梯形(如图2),利用这两个图形的面积,可以验证的等式是( )
A.a2+b2=(a+b)(a﹣b) B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)2=a2+2ab+b2 D.a2﹣b2=(a+b)(a﹣b)
7.如图是将正方形ABCD和正方形CEFG拼在一起的图形,点B,C,E在同一条直线上,连结BD,BF.若阴影部分△BDF的面积为8,则正方形ABCD的边长为( )
A.2 B.3 C.4 D.6
8.若x满足(2021﹣x)2+(x﹣2020)2=2019,则(2021﹣x)(x﹣2020)的值是( )
A.﹣1006 B.﹣1007 C.﹣1008 D.﹣1009
二.填空题(共8小题,满分40分)
9.若a2﹣b2=﹣,a+b=﹣,则a﹣b的值为 .
10.若x+y=4,xy=3,则x2+y2= .
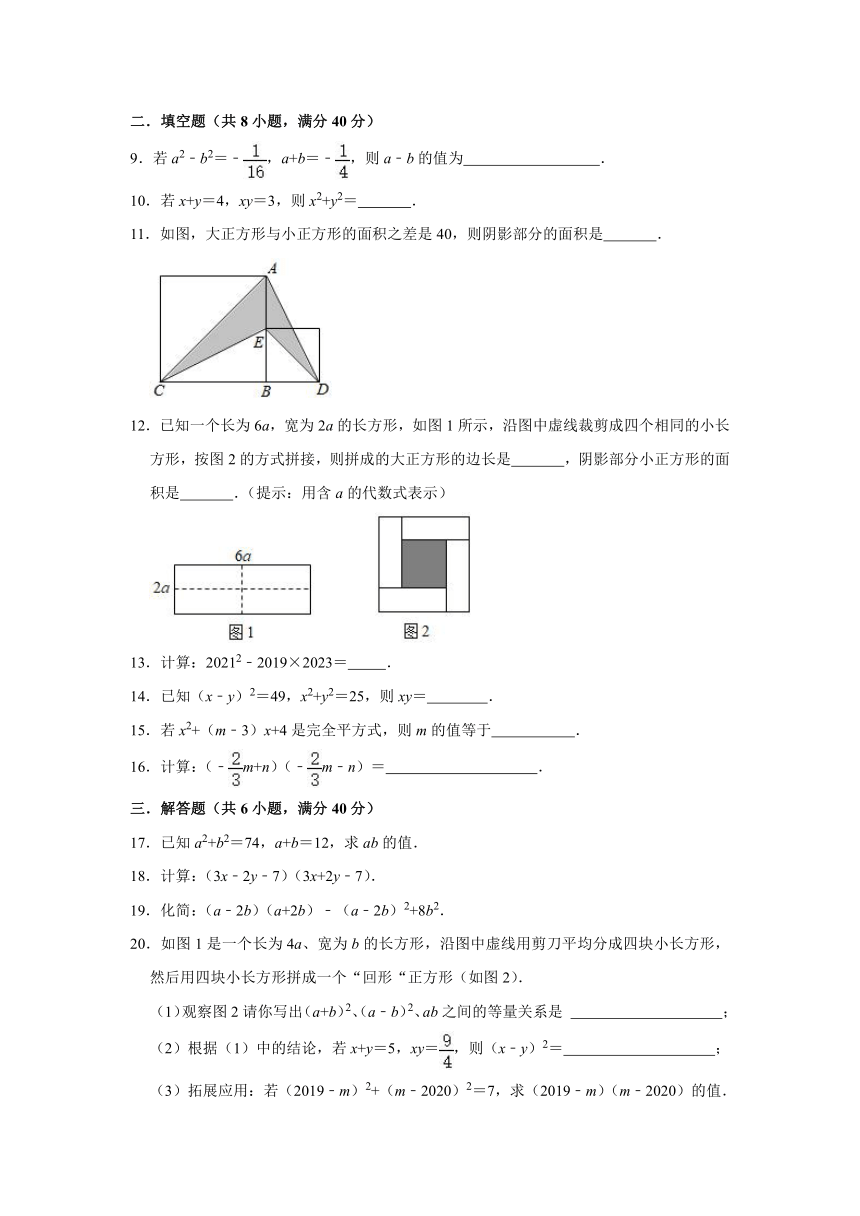
11.如图,大正方形与小正方形的面积之差是40,则阴影部分的面积是 .
12.已知一个长为6a,宽为2a的长方形,如图1所示,沿图中虚线裁剪成四个相同的小长方形,按图2的方式拼接,则拼成的大正方形的边长是 ,阴影部分小正方形的面积是 .(提示:用含a的代数式表示)
13.计算:20212﹣2019×2023= .
14.已知(x﹣y)2=49,x2+y2=25,则xy= .
15.若x2+(m﹣3)x+4是完全平方式,则m的值等于 .
16.计算:(﹣m+n)(﹣m﹣n)= .
三.解答题(共6小题,满分40分)
17.已知a2+b2=74,a+b=12,求ab的值.
18.计算:(3x﹣2y﹣7)(3x+2y﹣7).
19.化简:(a﹣2b)(a+2b)﹣(a﹣2b)2+8b2.
20.如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形“正方形(如图2).
(1)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(2)根据(1)中的结论,若x+y=5,xy=,则(x﹣y)2= ;
(3)拓展应用:若(2019﹣m)2+(m﹣2020)2=7,求(2019﹣m)(m﹣2020)的值.
21.我们将(a+b)2=a2+2ab+b2进行变形,如:a2+b2=(a+b)2﹣2ab,ab=等.根据以上变形解决下列问题:
(1)已知a2+b2=8,(a+b)2=48,则ab= .
(2)已知,若x满足(25﹣x)(x﹣10)=﹣15,求(25﹣x)2+(x﹣10)2的值.
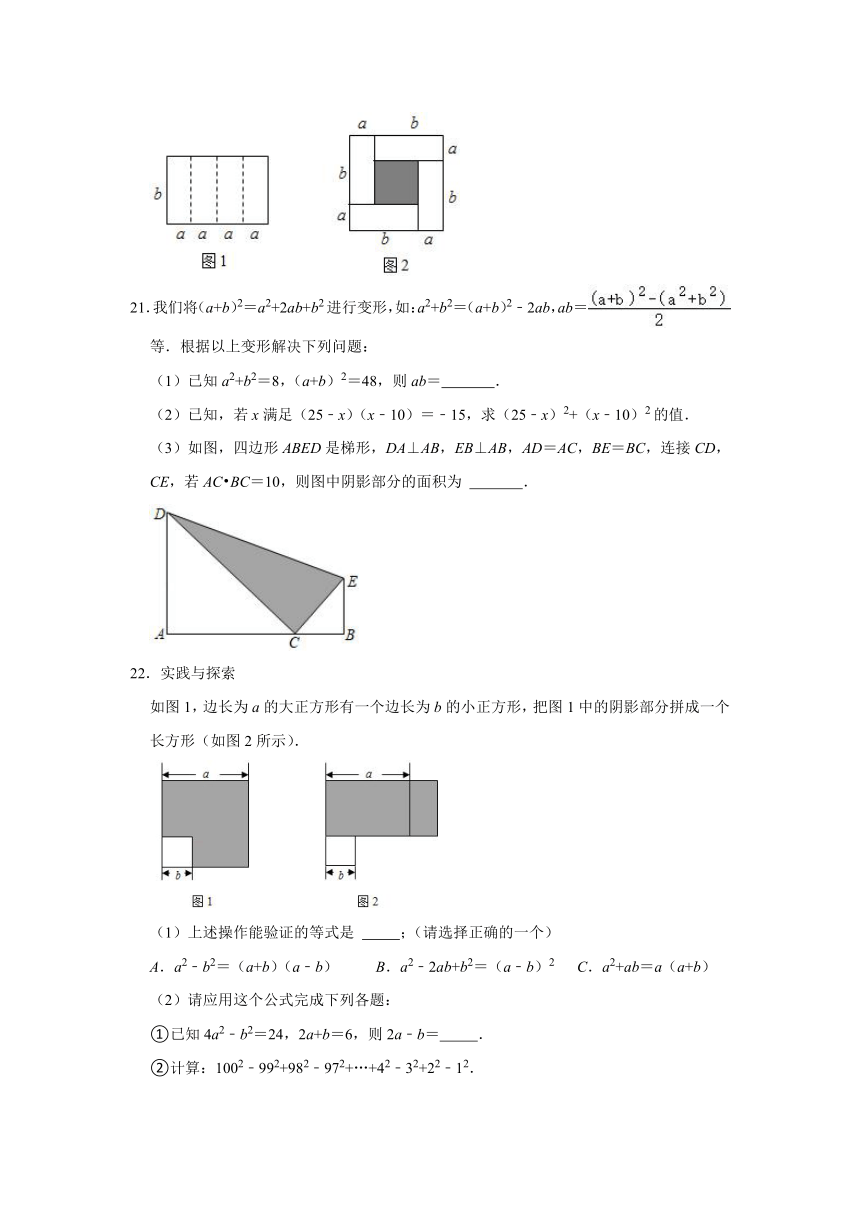
(3)如图,四边形ABED是梯形,DA⊥AB,EB⊥AB,AD=AC,BE=BC,连接CD,CE,若AC BC=10,则图中阴影部分的面积为 .
22.实践与探索
如图1,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A.a2﹣b2=(a+b)(a﹣b) B.a2﹣2ab+b2=(a﹣b)2 C.a2+ab=a(a+b)
(2)请应用这个公式完成下列各题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= .
②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12.
参考答案
一.选择题(共8小题,满分40分)
1.解:∵x2+mx+k是一个完全平方式,
∴x2+mx+k=x2+2×m x+k=(x+m)2,
∴k=m2.
故选:A.
2.解:A、(a﹣2)2=a2﹣4a+4,原计算错误,故此选项不符合题意;
B、(a+3)2=a2+6a+9,原计算错误,故此选项不符合题意;
C、(a﹣1)(a﹣2)=a2﹣3a+2,原计算正确,故此选项符合题意;
D、(a﹣2)(2﹣a)=﹣(a﹣2)(a﹣2)=﹣a2+4a﹣4,原计算错误,故此选项不符合题意;
故选:C.
3.解:(2n+1)2﹣(2n﹣1)2
=[(2n+1)﹣(2n﹣1)][(2n+1)+(2n﹣1)]
=8n,
故当n是正整数时,(2n+1)2﹣(2n﹣1)2是8的倍数.
故选:D.
4.解:∵a+b=6,a2﹣b2=30,
∴(a+b)(a﹣b)=30,
∴a﹣b=30÷6=5,
故选:A.
5.解:(3+2)×(32+22)×(34+24)×(38+28)
=(3﹣2)(3+2)×(32+22)×(34+24)×(38+28)
=(32﹣22)×(32+22)×(34+24)×(38+28)
=(34﹣24)×(34+24)×(38+28)
=(38﹣28)×(38+28)
=316﹣216.
故选:B.
6.解:∵图1中的阴影部分面积为:a2﹣b2,图2中阴影部分面积为:(2b+2a)(a﹣b),
∴a2﹣b2=(2b+2a)(a﹣b),即a2﹣b2=(a+b)(a﹣b),
故选:D.
7.解:如图,连接CF,
∵四边形ABCD和四边形CGFE都是正方形,
∴∠BDC=45°,∠GCF=45°,
∴∠BDC=∠GCF,
∴BD∥CF,
∴S△BDF=S△BCD=8,
∴S△BDF=BC×BC÷2=8.
BC=4,
故选:C.
8.解:设2021﹣x=a,x﹣2020=b,则(2021﹣x)2+(x﹣2020)2=a2+b2=2019,a+b=(2021﹣x)+(x﹣2020)=1,
所以,(2021﹣x)(x﹣2020)=ab=[(a+b)2﹣(a2+b2)]=×(12﹣2019)=﹣1009;
故选:D.
二.填空题(共8小题,满分40分)
9.解:因为a2﹣b2=﹣,
所以(a+b)(a﹣b)=﹣,
因为a+b=﹣,
所以a﹣b=﹣÷(﹣)=.
故答案为:.
10.解:∵x+y=4,xy=3,
∴x2+y2=(x+y)2﹣2xy
=42﹣2×3
=10.
故答案为10.
11.解:设大正方形的边长为a,小正方形的边长为b,
根据题意得a2﹣b2=40,
∴(a+b)(a﹣b)=40;
∵S阴=S△ACD﹣S△CDE,
∴S阴=×CD×AB﹣×CD×BE
=(a+b)a﹣(a+b)b
=(a+b)(a﹣b)
∵(a+b)(a﹣b)=40,
∴S阴=×40
=20.
故答案为:20.
12.解:由图可得,
图2中每个小长方形的长为3a,宽为a,
则拼成的大正方形的边长是:3a+a=4a,
阴影部分小正方形的边长是:3a﹣a=2a,
阴影部分小正方形的面积是:(2a)2=4a2,
故答案为:4a,4a2.
13.解:20212﹣2019×2023
=20212﹣(2021﹣2)(2021+2)
=20212﹣20212+22
=4.
故答案为:4.
14.解:因为(x﹣y)2=49,x2+y2=25,
所以x2+y2﹣(x﹣y)2=2xy=25﹣49=﹣24,、
所以xy=﹣12.
故答案为:﹣12.
15.解:∵多项式x2+(m﹣3)x+4是完全平方式,
∴(m﹣3)=±4,
解得:m=7或m=﹣1,
则m的值为﹣1或7.
故答案为:m=7或﹣1.
16.解:原式=(﹣m)2﹣n2
=(m)2﹣n2,
=m2﹣n2
故答案为:m2﹣n2.
三.解答题(共6小题,满分40分)
17.解:∵a2+b2=74,a+b=12,
∴(a+b)2=a2+b2+2ab=74+2ab=144.
∴ab=35.
18.解:原式=(3x﹣7)2﹣(2y)2
=9x2﹣42x+49﹣4y2.
19.解:原式=a2﹣4b2﹣a2+4ab﹣4b2+8b2
=4ab.
20.解:(1)由题意可得,图2的面积为:(a+b)2=(a﹣b)2+4ab,
故答案为:(a+b)2=(a﹣b)2+4ab;
(2)由(1)题结论(a+b)2=(a﹣b)2+4ab,
可得(a﹣b)2=(a+b)2﹣4ab,
∴x+y=5,xy=时,
(x﹣y)2
=(x+y)2﹣4xy
=52﹣4×
=25﹣9=16,
故答案为:16;
(3)由完全平方公式(a+b)2=a2+2ab+b2,
可得ab=,
∴当(2019﹣m)2+(m﹣2020)2=7时,
(2019﹣m)(m﹣2020)
=
=
=
=﹣3.
21.(1)∵a2+b2=8,(a+b)2=48,
∴ab===20,
(2)设25﹣x=a,x﹣10=b,
由(a+b)2=a2+2ab+b2进行变形得,
a2+b2=(a+b)2﹣2ab,
∴(25﹣x)2+(x﹣10)2
=[(25﹣x)+(x﹣10)] ﹣2(25﹣x)(x﹣10)
=15 ﹣2×(﹣15)
=225+30
=255,
(3)设AD=AC=a,BE=BC=b,
则图中阴影部分的面积为(a+b)(a+b)﹣(a +b )
=[(a+b) ﹣(a +b )]
=×2ab
=ab
=10
22.解:(1)图1中阴影部分的面积为两个正方形的面积差,即a2﹣b2,
图2中的阴影部分是长为(a+b),宽为(a﹣b)的长方形,因此面积为(a+b)(a﹣b),
所以有a2﹣b2=(a+b)(a﹣b),
故答案为:A;
(2)①∵4a2﹣b2=24,
∴(2a+b)(2a﹣b)=24,
又∵2a+b=6,
∴6(2a﹣b)=24,
即2a﹣b=4,
故答案为:4;
②∵1002﹣992=(100+99)(100﹣99)=100+99,
982﹣972=(98+97)(98﹣97)=98+97,
…
22﹣12=(2+1)(2﹣1)=2+1,
∴原式=100+99+98+97+…+4+3+2+1=5050
一.选择题(共8小题,满分40分)
1.若x2+mx+k是一个完全平方式,则k等于( )
A. B. C. D.m2
2.下列运算中,正确的是( )
A.(a﹣2)2=a2﹣4 B.(a+3)2=a2+9
C.(a﹣1)(a﹣2)=a2﹣3a+2 D.(a﹣2)(2﹣a)=a2﹣4
3.当n为正整数时,代数式(2n+1)2﹣(2n﹣1)2一定是下面哪个数的倍数( )
A.3 B.5 C.7 D.8
4.若a+b=6,a2﹣b2=30,则a﹣b=( )
A.5 B.6 C.10 D.15
5.(3+2)×(32+22)×(34+24)×(38+28)计算结果等于( )
A.1 B.316﹣216 C.332+232 D.332﹣232
6.如图1,在边长为a的正方形中剪去一个边长为b(b<a)的小正方形,把剩下部分拼成一个梯形(如图2),利用这两个图形的面积,可以验证的等式是( )
A.a2+b2=(a+b)(a﹣b) B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)2=a2+2ab+b2 D.a2﹣b2=(a+b)(a﹣b)
7.如图是将正方形ABCD和正方形CEFG拼在一起的图形,点B,C,E在同一条直线上,连结BD,BF.若阴影部分△BDF的面积为8,则正方形ABCD的边长为( )
A.2 B.3 C.4 D.6
8.若x满足(2021﹣x)2+(x﹣2020)2=2019,则(2021﹣x)(x﹣2020)的值是( )
A.﹣1006 B.﹣1007 C.﹣1008 D.﹣1009
二.填空题(共8小题,满分40分)
9.若a2﹣b2=﹣,a+b=﹣,则a﹣b的值为 .
10.若x+y=4,xy=3,则x2+y2= .
11.如图,大正方形与小正方形的面积之差是40,则阴影部分的面积是 .
12.已知一个长为6a,宽为2a的长方形,如图1所示,沿图中虚线裁剪成四个相同的小长方形,按图2的方式拼接,则拼成的大正方形的边长是 ,阴影部分小正方形的面积是 .(提示:用含a的代数式表示)
13.计算:20212﹣2019×2023= .
14.已知(x﹣y)2=49,x2+y2=25,则xy= .
15.若x2+(m﹣3)x+4是完全平方式,则m的值等于 .
16.计算:(﹣m+n)(﹣m﹣n)= .
三.解答题(共6小题,满分40分)
17.已知a2+b2=74,a+b=12,求ab的值.
18.计算:(3x﹣2y﹣7)(3x+2y﹣7).
19.化简:(a﹣2b)(a+2b)﹣(a﹣2b)2+8b2.
20.如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形“正方形(如图2).
(1)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(2)根据(1)中的结论,若x+y=5,xy=,则(x﹣y)2= ;
(3)拓展应用:若(2019﹣m)2+(m﹣2020)2=7,求(2019﹣m)(m﹣2020)的值.
21.我们将(a+b)2=a2+2ab+b2进行变形,如:a2+b2=(a+b)2﹣2ab,ab=等.根据以上变形解决下列问题:
(1)已知a2+b2=8,(a+b)2=48,则ab= .
(2)已知,若x满足(25﹣x)(x﹣10)=﹣15,求(25﹣x)2+(x﹣10)2的值.
(3)如图,四边形ABED是梯形,DA⊥AB,EB⊥AB,AD=AC,BE=BC,连接CD,CE,若AC BC=10,则图中阴影部分的面积为 .
22.实践与探索
如图1,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A.a2﹣b2=(a+b)(a﹣b) B.a2﹣2ab+b2=(a﹣b)2 C.a2+ab=a(a+b)
(2)请应用这个公式完成下列各题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= .
②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12.
参考答案
一.选择题(共8小题,满分40分)
1.解:∵x2+mx+k是一个完全平方式,
∴x2+mx+k=x2+2×m x+k=(x+m)2,
∴k=m2.
故选:A.
2.解:A、(a﹣2)2=a2﹣4a+4,原计算错误,故此选项不符合题意;
B、(a+3)2=a2+6a+9,原计算错误,故此选项不符合题意;
C、(a﹣1)(a﹣2)=a2﹣3a+2,原计算正确,故此选项符合题意;
D、(a﹣2)(2﹣a)=﹣(a﹣2)(a﹣2)=﹣a2+4a﹣4,原计算错误,故此选项不符合题意;
故选:C.
3.解:(2n+1)2﹣(2n﹣1)2
=[(2n+1)﹣(2n﹣1)][(2n+1)+(2n﹣1)]
=8n,
故当n是正整数时,(2n+1)2﹣(2n﹣1)2是8的倍数.
故选:D.
4.解:∵a+b=6,a2﹣b2=30,
∴(a+b)(a﹣b)=30,
∴a﹣b=30÷6=5,
故选:A.
5.解:(3+2)×(32+22)×(34+24)×(38+28)
=(3﹣2)(3+2)×(32+22)×(34+24)×(38+28)
=(32﹣22)×(32+22)×(34+24)×(38+28)
=(34﹣24)×(34+24)×(38+28)
=(38﹣28)×(38+28)
=316﹣216.
故选:B.
6.解:∵图1中的阴影部分面积为:a2﹣b2,图2中阴影部分面积为:(2b+2a)(a﹣b),
∴a2﹣b2=(2b+2a)(a﹣b),即a2﹣b2=(a+b)(a﹣b),
故选:D.
7.解:如图,连接CF,
∵四边形ABCD和四边形CGFE都是正方形,
∴∠BDC=45°,∠GCF=45°,
∴∠BDC=∠GCF,
∴BD∥CF,
∴S△BDF=S△BCD=8,
∴S△BDF=BC×BC÷2=8.
BC=4,
故选:C.
8.解:设2021﹣x=a,x﹣2020=b,则(2021﹣x)2+(x﹣2020)2=a2+b2=2019,a+b=(2021﹣x)+(x﹣2020)=1,
所以,(2021﹣x)(x﹣2020)=ab=[(a+b)2﹣(a2+b2)]=×(12﹣2019)=﹣1009;
故选:D.
二.填空题(共8小题,满分40分)
9.解:因为a2﹣b2=﹣,
所以(a+b)(a﹣b)=﹣,
因为a+b=﹣,
所以a﹣b=﹣÷(﹣)=.
故答案为:.
10.解:∵x+y=4,xy=3,
∴x2+y2=(x+y)2﹣2xy
=42﹣2×3
=10.
故答案为10.
11.解:设大正方形的边长为a,小正方形的边长为b,
根据题意得a2﹣b2=40,
∴(a+b)(a﹣b)=40;
∵S阴=S△ACD﹣S△CDE,
∴S阴=×CD×AB﹣×CD×BE
=(a+b)a﹣(a+b)b
=(a+b)(a﹣b)
∵(a+b)(a﹣b)=40,
∴S阴=×40
=20.
故答案为:20.
12.解:由图可得,
图2中每个小长方形的长为3a,宽为a,
则拼成的大正方形的边长是:3a+a=4a,
阴影部分小正方形的边长是:3a﹣a=2a,
阴影部分小正方形的面积是:(2a)2=4a2,
故答案为:4a,4a2.
13.解:20212﹣2019×2023
=20212﹣(2021﹣2)(2021+2)
=20212﹣20212+22
=4.
故答案为:4.
14.解:因为(x﹣y)2=49,x2+y2=25,
所以x2+y2﹣(x﹣y)2=2xy=25﹣49=﹣24,、
所以xy=﹣12.
故答案为:﹣12.
15.解:∵多项式x2+(m﹣3)x+4是完全平方式,
∴(m﹣3)=±4,
解得:m=7或m=﹣1,
则m的值为﹣1或7.
故答案为:m=7或﹣1.
16.解:原式=(﹣m)2﹣n2
=(m)2﹣n2,
=m2﹣n2
故答案为:m2﹣n2.
三.解答题(共6小题,满分40分)
17.解:∵a2+b2=74,a+b=12,
∴(a+b)2=a2+b2+2ab=74+2ab=144.
∴ab=35.
18.解:原式=(3x﹣7)2﹣(2y)2
=9x2﹣42x+49﹣4y2.
19.解:原式=a2﹣4b2﹣a2+4ab﹣4b2+8b2
=4ab.
20.解:(1)由题意可得,图2的面积为:(a+b)2=(a﹣b)2+4ab,
故答案为:(a+b)2=(a﹣b)2+4ab;
(2)由(1)题结论(a+b)2=(a﹣b)2+4ab,
可得(a﹣b)2=(a+b)2﹣4ab,
∴x+y=5,xy=时,
(x﹣y)2
=(x+y)2﹣4xy
=52﹣4×
=25﹣9=16,
故答案为:16;
(3)由完全平方公式(a+b)2=a2+2ab+b2,
可得ab=,
∴当(2019﹣m)2+(m﹣2020)2=7时,
(2019﹣m)(m﹣2020)
=
=
=
=﹣3.
21.(1)∵a2+b2=8,(a+b)2=48,
∴ab===20,
(2)设25﹣x=a,x﹣10=b,
由(a+b)2=a2+2ab+b2进行变形得,
a2+b2=(a+b)2﹣2ab,
∴(25﹣x)2+(x﹣10)2
=[(25﹣x)+(x﹣10)] ﹣2(25﹣x)(x﹣10)
=15 ﹣2×(﹣15)
=225+30
=255,
(3)设AD=AC=a,BE=BC=b,
则图中阴影部分的面积为(a+b)(a+b)﹣(a +b )
=[(a+b) ﹣(a +b )]
=×2ab
=ab
=10
22.解:(1)图1中阴影部分的面积为两个正方形的面积差,即a2﹣b2,
图2中的阴影部分是长为(a+b),宽为(a﹣b)的长方形,因此面积为(a+b)(a﹣b),
所以有a2﹣b2=(a+b)(a﹣b),
故答案为:A;
(2)①∵4a2﹣b2=24,
∴(2a+b)(2a﹣b)=24,
又∵2a+b=6,
∴6(2a﹣b)=24,
即2a﹣b=4,
故答案为:4;
②∵1002﹣992=(100+99)(100﹣99)=100+99,
982﹣972=(98+97)(98﹣97)=98+97,
…
22﹣12=(2+1)(2﹣1)=2+1,
∴原式=100+99+98+97+…+4+3+2+1=5050
