15.1.4(3)_多项式乘以多项式课件_人教新课标版
文档属性
| 名称 | 15.1.4(3)_多项式乘以多项式课件_人教新课标版 |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-29 11:15:01 | ||
图片预览







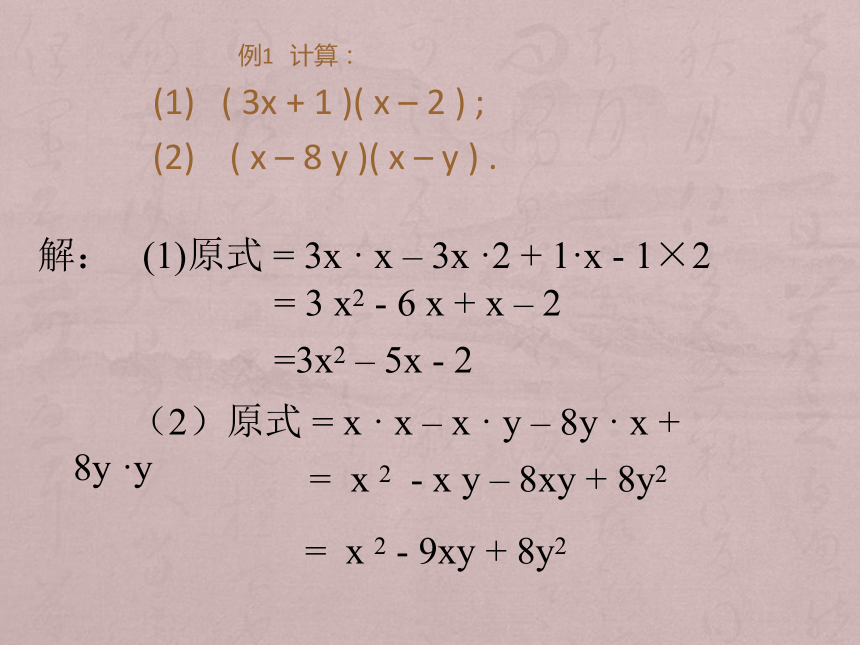
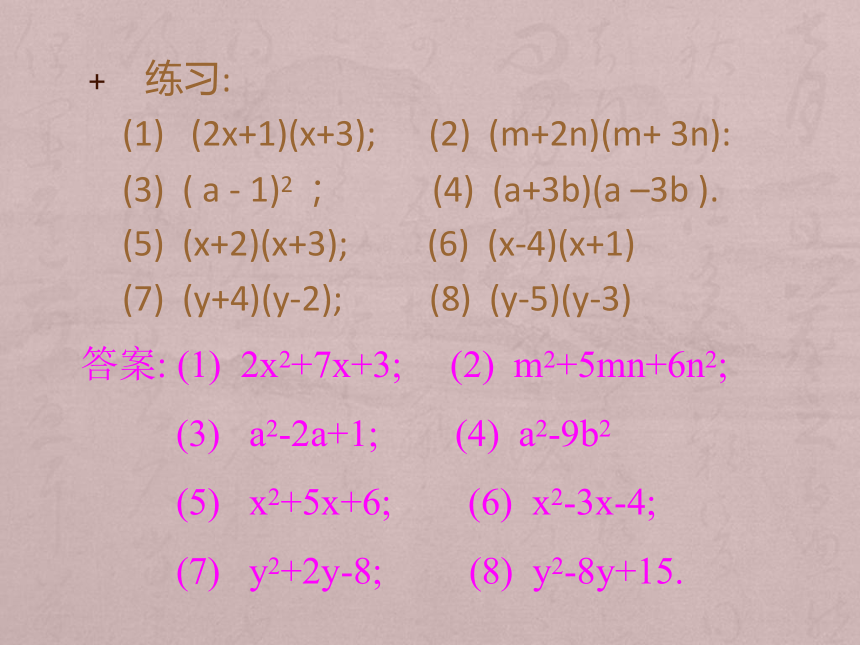
文档简介
(共24张PPT)
如何进行单项式乘单项式的运算?
单×单
=(系数×系数)(同底数幂×同底数幂)(单独的幂)
知识 & 回顾
( 2a2b3c) (-3ab)
= -6a3b4c
如何进行单项式乘多项式的运算?
知识 & 回顾
单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加.
=
为了把校园建设成为花园式的学
校,经研究决定将原有的长为a米,
宽为b米的足球场向宿舍楼方向加长
m米,向厕所方向加宽n米,扩建成为美化校园绿草地。你是学校的小主人,你能帮助学校计算出扩展后绿地的面积吗?
a
m
b
n
方案一:S=a b + a n + b m + m n
a
m
b
n
方案二:S= b ( a + m ) + n ( a + m )
方案三: S= a ( b + n ) + m ( b + n )
方案四: S=( a + m ) ( b + n )
∴( a + m )( b + n ) = a ( b + n ) + m ( b + n )
=a b + a n + b m +m n
观察上述式子,你能的得到(x-3)(x-6)的结果吗
或( a + m )( b + n ) = b ( a + m ) + n ( a+m)
= a b + b m + a n + m n
( x – 3 )( y – 6 ) = x ( y – 6 ) – 3 ( y – 6 )
= x y – 6x – 3y + 18
∵四种方案算出的面积相等
归纳得出: 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)( m+n)=am+an+bm+bn
( a+b)(m+n)
= a(m+n)+b(m+n)
= am+an+bm+bn
例1 计算:
(1) ( 3x + 1 )( x – 2 ) ;
(2) ( x – 8 y )( x – y ) .
解: (1)原式 = 3x · x – 3x ·2 + 1·x - 1×2
(2)原式 = x · x – x · y – 8y · x + 8y ·y
= 3 x2 - 6 x + x – 2
=3x2 – 5x - 2
= x 2 - x y – 8xy + 8y2
= x 2 - 9xy + 8y2
练习:
(1) (2x+1)(x+3); (2) (m+2n)(m+ 3n):
(3) ( a - 1)2 ; (4) (a+3b)(a –3b ).
(5) (x+2)(x+3); (6) (x-4)(x+1)
(7) (y+4)(y-2); (8) (y-5)(y-3)
答案: (1) 2x2+7x+3; (2) m2+5mn+6n2;
(3) a2-2a+1; (4) a2-9b2
(5) x2+5x+6; (6) x2-3x-4;
(7) y2+2y-8; (8) y2-8y+15.
计算:
(1) ( 3x -1 )( x +2 ) ;
(2) ( x – 3y )( x – y ) .
(3) (x+y)(x2-xy+y2)
1.计算下列各式:
练习:
(1) (2x+1)(x+3); (2) (m+2n)(m+ 3n):
(3) ( a - 1)2 ; (4) (a+3b)(a –3b ).
(5) (x+2)(x+3); (6) (x-4)(x+1)
(7) (y+4)(y-2); (8) (y-5)(y-3)
(x+2)(x+3) = x2 + 5x+6;
(x-4)(x+1) = x2 – 3x-4
(y+4)(y-2) = y2 + 2y-8
(y-5)(y-3). = y2- 8y+15
观察上述式子,你可以 得出一个什么规律吗?
(x+p)(x+q) = x2 + (p+q) x + p q
根据上述结论计算:
(1) (x+1)(x+2)=
(2) (x+1)(x-2)=
(3) (x-1)(x+2)=
(4) (x-1)(x-2)=
x2+3x+2
x2-x-2
x2+x-2
x2-3x+2
(x+p)(x+q) = x2 + (p+q) x + p q
拓展与应用
练习:
确定下列各式中m的值:
(1) (x+4)(x+9) = x2 + m x + 36
(2) (x-2)(x-18) = x + m x + 36
(3) (x+3)(x+p) = x + m x + 36
(4) (x-6) (x-p) = x + m x + 36
(5) (x+p)(x+q) = x + m x + 36
(p,q为正整数)
(1) m =13
(2) m = - 20
(3) p =12, m= 15
(4) p= -6, m= -12
(5) p = 4,q = 9, m =13
p=2,q = 18, m=20
p = 3, q =12, m=15
p=6, q= 6, m=12
确定下列各式中m与p的值:
(1) (x+4)(x+9) = x2 + m x + 36
(2) (x-2)(x-18) = x2 + m x + 36
(3) (x+3)(x+p) = x2 + m x + 36
(4) (x-6) (x-p) = x2 + m x + 36
(5) (x+p)(x+q) = x2 + m x + 36
(1) m =13
(2) m = - 20
(3) p =12, m= 15
(4) p= 6, m= -12
(5) p = 4,q = 9, m =13
p=2,q = 18, m=20
p = 3, q =12, m=15
p=6, q= 6, m=12
拓展与应用
(x+p)(x+q) = x2 + (p+q) x + p q
(p,q为正整数)
…………
拓展提高
c
c
a
b
1、有一长方形耕地,其中长为a,宽为b,现要在该耕地上种植两块防风带,如图所示的绿色部分,其中横向防风带为长方形,纵向防风带为平行四边形,则剩余耕地面积为( )
A、bc-ab+ac+c2
B、ab-bc-ac+c2
C、a2+ab+bc-ac
D、b2-bc+a2-ab
B
2、如果(x+a)(x+b)的积中不含x的一次项,那么a、b一定满足( )
A、互为倒数 B、互为相反数
C、a=b=0 D、ab=0
拓展提高
B
3.若(x2+px+q)(x2-3x+2)的乘积中不含x2和x3项,求p,q的值
4、观察下列各式:
(x-1)(x+1)=x2-1
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
……
根据前面各式的规律可得到:
(x-1)(xn+xn-1+xn-2+……+x+1)=________
拓展提高
Xn+1-1
5、观察下列各式:
(x-1)(x2+x+1)=x3-1
(2a+b)(4a2-2ab+b2)=8a3+b3
(m-3n)(m2+3mn+9n2)=m3-27n3
(1)请你用字母表示出上述计算的规律;
(2)利用上面的规律计算:
拓展提高
小 结
1、多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)( m+n)=am+an+bm+bn
2、多项式与多项式相乘时,多项式的每一项都应该带上它前面的正负号。多项式是单项式的和,每一项都包括前面的符号,在计算时一定要注意确定各项的符号。
4、在数学知识的学习中,“转化”思想是的重要思想方法。在今天的学习中,第一步是“转化”为多项式与单项式相乘,第二步是“转化”为单项式乘法。即将新的知识、方法化为已知的数学知识、方法。从而使学习能够进行。
3、(x+p)(x+q) = x2 + (p+q) x + p q
课外作业:
课本P.150 第11题
解方程与不等式:
(1) (x-3)(x-2)+18 = (x+9)(x+1);
(2) (3x+4)(3x-4) <9(x-2)(x+3).
如何进行单项式乘单项式的运算?
单×单
=(系数×系数)(同底数幂×同底数幂)(单独的幂)
知识 & 回顾
( 2a2b3c) (-3ab)
= -6a3b4c
如何进行单项式乘多项式的运算?
知识 & 回顾
单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加.
=
为了把校园建设成为花园式的学
校,经研究决定将原有的长为a米,
宽为b米的足球场向宿舍楼方向加长
m米,向厕所方向加宽n米,扩建成为美化校园绿草地。你是学校的小主人,你能帮助学校计算出扩展后绿地的面积吗?
a
m
b
n
方案一:S=a b + a n + b m + m n
a
m
b
n
方案二:S= b ( a + m ) + n ( a + m )
方案三: S= a ( b + n ) + m ( b + n )
方案四: S=( a + m ) ( b + n )
∴( a + m )( b + n ) = a ( b + n ) + m ( b + n )
=a b + a n + b m +m n
观察上述式子,你能的得到(x-3)(x-6)的结果吗
或( a + m )( b + n ) = b ( a + m ) + n ( a+m)
= a b + b m + a n + m n
( x – 3 )( y – 6 ) = x ( y – 6 ) – 3 ( y – 6 )
= x y – 6x – 3y + 18
∵四种方案算出的面积相等
归纳得出: 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)( m+n)=am+an+bm+bn
( a+b)(m+n)
= a(m+n)+b(m+n)
= am+an+bm+bn
例1 计算:
(1) ( 3x + 1 )( x – 2 ) ;
(2) ( x – 8 y )( x – y ) .
解: (1)原式 = 3x · x – 3x ·2 + 1·x - 1×2
(2)原式 = x · x – x · y – 8y · x + 8y ·y
= 3 x2 - 6 x + x – 2
=3x2 – 5x - 2
= x 2 - x y – 8xy + 8y2
= x 2 - 9xy + 8y2
练习:
(1) (2x+1)(x+3); (2) (m+2n)(m+ 3n):
(3) ( a - 1)2 ; (4) (a+3b)(a –3b ).
(5) (x+2)(x+3); (6) (x-4)(x+1)
(7) (y+4)(y-2); (8) (y-5)(y-3)
答案: (1) 2x2+7x+3; (2) m2+5mn+6n2;
(3) a2-2a+1; (4) a2-9b2
(5) x2+5x+6; (6) x2-3x-4;
(7) y2+2y-8; (8) y2-8y+15.
计算:
(1) ( 3x -1 )( x +2 ) ;
(2) ( x – 3y )( x – y ) .
(3) (x+y)(x2-xy+y2)
1.计算下列各式:
练习:
(1) (2x+1)(x+3); (2) (m+2n)(m+ 3n):
(3) ( a - 1)2 ; (4) (a+3b)(a –3b ).
(5) (x+2)(x+3); (6) (x-4)(x+1)
(7) (y+4)(y-2); (8) (y-5)(y-3)
(x+2)(x+3) = x2 + 5x+6;
(x-4)(x+1) = x2 – 3x-4
(y+4)(y-2) = y2 + 2y-8
(y-5)(y-3). = y2- 8y+15
观察上述式子,你可以 得出一个什么规律吗?
(x+p)(x+q) = x2 + (p+q) x + p q
根据上述结论计算:
(1) (x+1)(x+2)=
(2) (x+1)(x-2)=
(3) (x-1)(x+2)=
(4) (x-1)(x-2)=
x2+3x+2
x2-x-2
x2+x-2
x2-3x+2
(x+p)(x+q) = x2 + (p+q) x + p q
拓展与应用
练习:
确定下列各式中m的值:
(1) (x+4)(x+9) = x2 + m x + 36
(2) (x-2)(x-18) = x + m x + 36
(3) (x+3)(x+p) = x + m x + 36
(4) (x-6) (x-p) = x + m x + 36
(5) (x+p)(x+q) = x + m x + 36
(p,q为正整数)
(1) m =13
(2) m = - 20
(3) p =12, m= 15
(4) p= -6, m= -12
(5) p = 4,q = 9, m =13
p=2,q = 18, m=20
p = 3, q =12, m=15
p=6, q= 6, m=12
确定下列各式中m与p的值:
(1) (x+4)(x+9) = x2 + m x + 36
(2) (x-2)(x-18) = x2 + m x + 36
(3) (x+3)(x+p) = x2 + m x + 36
(4) (x-6) (x-p) = x2 + m x + 36
(5) (x+p)(x+q) = x2 + m x + 36
(1) m =13
(2) m = - 20
(3) p =12, m= 15
(4) p= 6, m= -12
(5) p = 4,q = 9, m =13
p=2,q = 18, m=20
p = 3, q =12, m=15
p=6, q= 6, m=12
拓展与应用
(x+p)(x+q) = x2 + (p+q) x + p q
(p,q为正整数)
…………
拓展提高
c
c
a
b
1、有一长方形耕地,其中长为a,宽为b,现要在该耕地上种植两块防风带,如图所示的绿色部分,其中横向防风带为长方形,纵向防风带为平行四边形,则剩余耕地面积为( )
A、bc-ab+ac+c2
B、ab-bc-ac+c2
C、a2+ab+bc-ac
D、b2-bc+a2-ab
B
2、如果(x+a)(x+b)的积中不含x的一次项,那么a、b一定满足( )
A、互为倒数 B、互为相反数
C、a=b=0 D、ab=0
拓展提高
B
3.若(x2+px+q)(x2-3x+2)的乘积中不含x2和x3项,求p,q的值
4、观察下列各式:
(x-1)(x+1)=x2-1
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
……
根据前面各式的规律可得到:
(x-1)(xn+xn-1+xn-2+……+x+1)=________
拓展提高
Xn+1-1
5、观察下列各式:
(x-1)(x2+x+1)=x3-1
(2a+b)(4a2-2ab+b2)=8a3+b3
(m-3n)(m2+3mn+9n2)=m3-27n3
(1)请你用字母表示出上述计算的规律;
(2)利用上面的规律计算:
拓展提高
小 结
1、多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)( m+n)=am+an+bm+bn
2、多项式与多项式相乘时,多项式的每一项都应该带上它前面的正负号。多项式是单项式的和,每一项都包括前面的符号,在计算时一定要注意确定各项的符号。
4、在数学知识的学习中,“转化”思想是的重要思想方法。在今天的学习中,第一步是“转化”为多项式与单项式相乘,第二步是“转化”为单项式乘法。即将新的知识、方法化为已知的数学知识、方法。从而使学习能够进行。
3、(x+p)(x+q) = x2 + (p+q) x + p q
课外作业:
课本P.150 第11题
解方程与不等式:
(1) (x-3)(x-2)+18 = (x+9)(x+1);
(2) (3x+4)(3x-4) <9(x-2)(x+3).
