2021--2022学年苏科版八年级数学上册4.3. 实数 课件(共23张PPT)
文档属性
| 名称 | 2021--2022学年苏科版八年级数学上册4.3. 实数 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 344.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 09:44:24 | ||
图片预览




文档简介
(共23张PPT)
2021
4.3 实数(1)
八年级上册
复习回顾
1
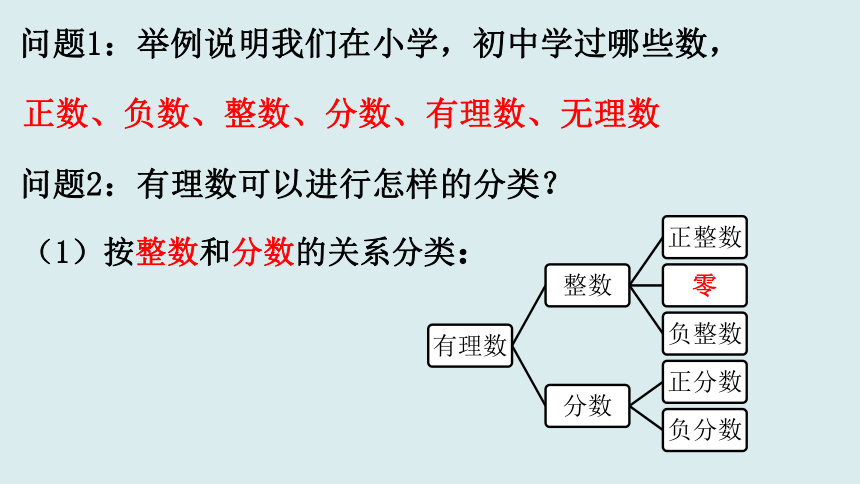
问题1:举例说明我们在小学,初中学过哪些数,
问题2:有理数可以进行怎样的分类?
正数、负数、整数、分数、有理数、无理数
(1)按整数和分数的关系分类:
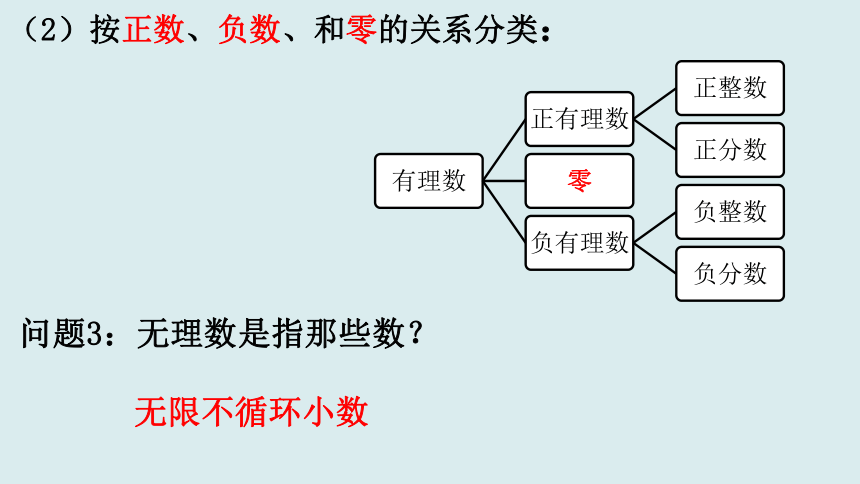
(2)按正数、负数、和零的关系分类:
问题3:无理数是指那些数?
无限不循环小数
教学新知
2
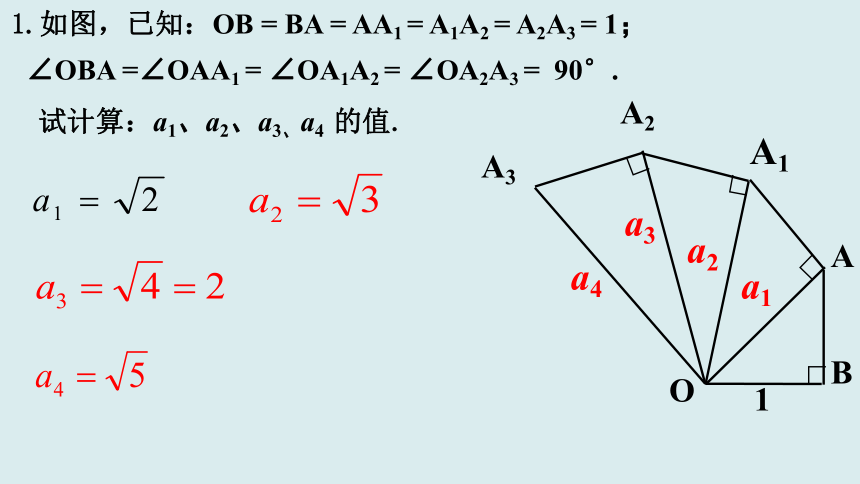
1.如图,已知:OB = BA = AA1 = A1A2 = A2A3 = 1;
∠OBA =∠OAA1 = ∠OA1A2 = ∠OA2A3 = 90°.
试计算:a1、a2、a3、a4 的值.
a1
a2
a3
a4
B
A
∟
∟
∟
∟
A1
A2
A3
O
1
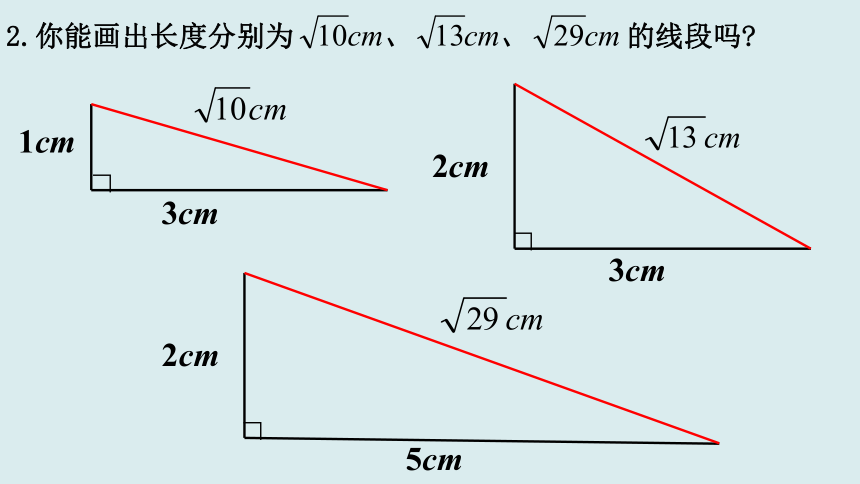
2.你能画出长度分别为 的线段吗
∟
3cm
1cm
∟
3cm
2cm
∟
5cm
2cm
我们知道这里的 是 .
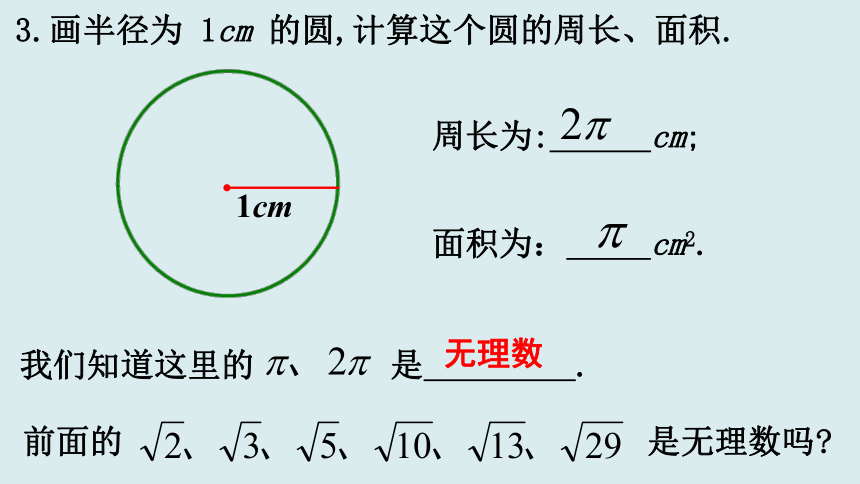
3.画半径为 1cm 的圆,计算这个圆的周长、面积.
1cm
周长为: cm;
面积为: cm2.
无理数
前面的 是无理数吗
无理数的概念:
无限不循环小数称为无理数.
= 1.414 213 562 373 095 048 801 688 7…
它是一个无限不循环小数.
故为无理数.
同样地:
等都是无理数.
另外,像0.1010010001… ,它是人为构造的无限不循环小数,因此也是无理数.
无理数的常见类型:
根号型, 如:
型, 如:
构造型(有一定的规律,但不循环的无限小数)
如:
0.123456789101112…、0.1010010001… 等.
开方开不尽的数
例1、判断下列数哪些是有理数?哪些是无理数?
解:
有理数是:
无理数是:
思考:那么,有理数和无理数合在一起叫什么呢?
实数的概念:
有理数和无理数统称为实数.
实数
有理数
无理数
0
正无理数
负无理数
正有理数
负有理数
有限小数或
无限循环小数.
无限不循环小数.
(1)可按有理数和无理数进行分类:
(2)可按正实数、0、负实数进行分类:
思考:有理数都可以用数轴上的点来表示,
那么,无理数可以用数轴上的点来表示吗?
1
O
2
-2
-1
∟
A
上图中, 点 A 表示 .
∟
B
点 B 表示 .
每一个实数都可以用数轴上的一个点来表示,数轴上的每一个点都表示一个实数,因此,实数与数轴上的点是一一对应的.
从图中可以看出,无理数可以用数轴上的点来表示。
课堂练习
3
一、判断
1.实数不是有理数就是无理数.( )
2.无理数都是无限不循环小数.( )
3.无理数都是无限小数.( )
4.带根号的数都是无理数.( )
5.无理数一定都带根号.( )
6.两个无理数之积不一定是无理数.( )
7.两个无理数之和一定是无理数.( )
8.数轴上的任何一点都可以表示实数.( )
×
×
×
,-6 ,9.3 ,42 ,0 ,-0.33 ,0.333... , 1.41421356 , -2π ,3.3030030003... , -3.1415926
正数集合:____________________________________
负数集合:____________________________________
有理数集合:__________________________________
无理数集合:__________________________________
(2)无理数集合: …
2、把下列各数填人相应的集合内:
(1)有理数集合: …
(3)正实数集合: …
(4)负实数集合: …
课堂小结
4
实数
无理数
无限不循环的小数叫做无理数.
实数及其分类
实数与数轴上的点的关系
有理数
无理数
0
正无理数
负无理数
正有理数
负有理数
拓展提升
5
1、在实数 , , π, 中,是无理数的是( )
A. B.
C.π D.
C
2.和数轴上的点一一对应的数是( )
A.整数 B.有理数
C.无理数 D.实数
D
3、在数轴上找出表示 的点.
O
-3
-2
-1
3
2
1
2021
4.3 实数(1)
八年级上册
复习回顾
1
问题1:举例说明我们在小学,初中学过哪些数,
问题2:有理数可以进行怎样的分类?
正数、负数、整数、分数、有理数、无理数
(1)按整数和分数的关系分类:
(2)按正数、负数、和零的关系分类:
问题3:无理数是指那些数?
无限不循环小数
教学新知
2
1.如图,已知:OB = BA = AA1 = A1A2 = A2A3 = 1;
∠OBA =∠OAA1 = ∠OA1A2 = ∠OA2A3 = 90°.
试计算:a1、a2、a3、a4 的值.
a1
a2
a3
a4
B
A
∟
∟
∟
∟
A1
A2
A3
O
1
2.你能画出长度分别为 的线段吗
∟
3cm
1cm
∟
3cm
2cm
∟
5cm
2cm
我们知道这里的 是 .
3.画半径为 1cm 的圆,计算这个圆的周长、面积.
1cm
周长为: cm;
面积为: cm2.
无理数
前面的 是无理数吗
无理数的概念:
无限不循环小数称为无理数.
= 1.414 213 562 373 095 048 801 688 7…
它是一个无限不循环小数.
故为无理数.
同样地:
等都是无理数.
另外,像0.1010010001… ,它是人为构造的无限不循环小数,因此也是无理数.
无理数的常见类型:
根号型, 如:
型, 如:
构造型(有一定的规律,但不循环的无限小数)
如:
0.123456789101112…、0.1010010001… 等.
开方开不尽的数
例1、判断下列数哪些是有理数?哪些是无理数?
解:
有理数是:
无理数是:
思考:那么,有理数和无理数合在一起叫什么呢?
实数的概念:
有理数和无理数统称为实数.
实数
有理数
无理数
0
正无理数
负无理数
正有理数
负有理数
有限小数或
无限循环小数.
无限不循环小数.
(1)可按有理数和无理数进行分类:
(2)可按正实数、0、负实数进行分类:
思考:有理数都可以用数轴上的点来表示,
那么,无理数可以用数轴上的点来表示吗?
1
O
2
-2
-1
∟
A
上图中, 点 A 表示 .
∟
B
点 B 表示 .
每一个实数都可以用数轴上的一个点来表示,数轴上的每一个点都表示一个实数,因此,实数与数轴上的点是一一对应的.
从图中可以看出,无理数可以用数轴上的点来表示。
课堂练习
3
一、判断
1.实数不是有理数就是无理数.( )
2.无理数都是无限不循环小数.( )
3.无理数都是无限小数.( )
4.带根号的数都是无理数.( )
5.无理数一定都带根号.( )
6.两个无理数之积不一定是无理数.( )
7.两个无理数之和一定是无理数.( )
8.数轴上的任何一点都可以表示实数.( )
×
×
×
,-6 ,9.3 ,42 ,0 ,-0.33 ,0.333... , 1.41421356 , -2π ,3.3030030003... , -3.1415926
正数集合:____________________________________
负数集合:____________________________________
有理数集合:__________________________________
无理数集合:__________________________________
(2)无理数集合: …
2、把下列各数填人相应的集合内:
(1)有理数集合: …
(3)正实数集合: …
(4)负实数集合: …
课堂小结
4
实数
无理数
无限不循环的小数叫做无理数.
实数及其分类
实数与数轴上的点的关系
有理数
无理数
0
正无理数
负无理数
正有理数
负有理数
拓展提升
5
1、在实数 , , π, 中,是无理数的是( )
A. B.
C.π D.
C
2.和数轴上的点一一对应的数是( )
A.整数 B.有理数
C.无理数 D.实数
D
3、在数轴上找出表示 的点.
O
-3
-2
-1
3
2
1
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
