2021-2022学年人教版七年级数学上册第一章 有理数1.4.2有理数的除法课件(共15张PPT)
文档属性
| 名称 | 2021-2022学年人教版七年级数学上册第一章 有理数1.4.2有理数的除法课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 466.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 09:45:38 | ||
图片预览





文档简介
(共15张PPT)
1.4.2 有理数的除法
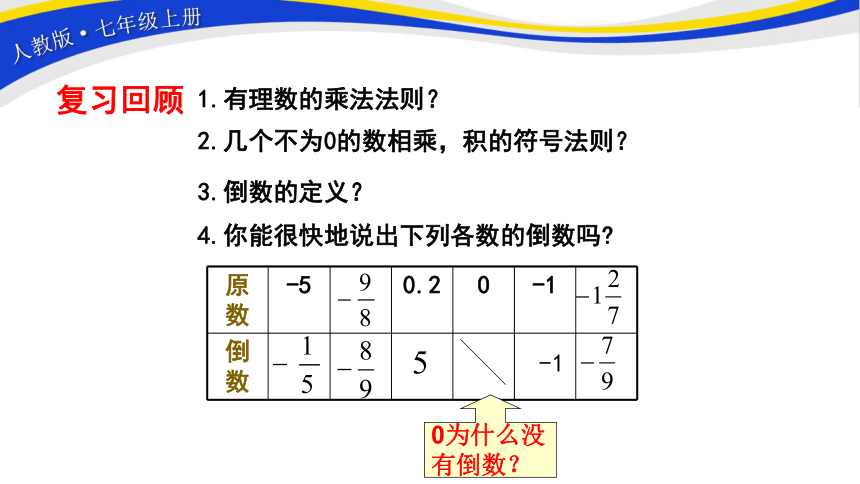
复习回顾
1.有理数的乘法法则?
3.倒数的定义?
2.几个不为0的数相乘,积的符号法则?
4.你能很快地说出下列各数的倒数吗
原数 -5 0.2 0 -1
倒数
0为什么没有倒数?
-1
探究活动
怎样计算8÷(-4)呢?
8÷(-4)=
8×( )=
-2
于是
8×( )
8÷(-4)=
-2
因为(-2)×(-4)=8
所以8÷(-4)=-2
换其他数的除法进行类似讨论,是否仍有除以a(a≠0)可以转化为乘 ?
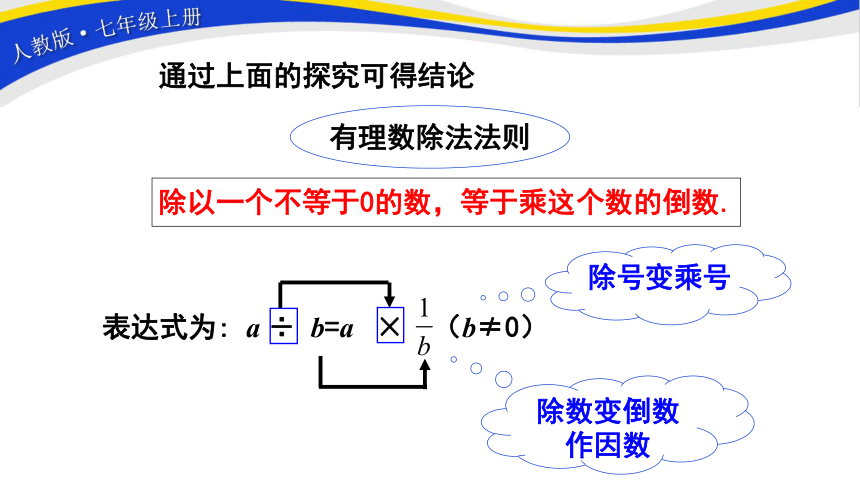
有理数除法法则
除以一个不等于0的数,等于乘这个数的倒数.
除号变乘号
除数变倒数作因数
通过上面的探究可得结论
表达式为: a ÷ b=a × (b≠0)
利用上面的除法法则计算下列各题:
(1) 27÷ (-9) =
(2) (-72)÷(-9)=
(3) 0÷ (-2) =
(4) 48÷ (-6) =
(5) (-18)÷6=
(7) (-27)÷(-9)=
-3
8
0
-8
-3
3
思考:从上面我们能发现商的符号有什么规律?
有理数除法法则的另一种说法:
两数相除,同号得 ,异号得 ,并把绝对值相 .0除以任何一个不等于0的数,都得 .
正
负
除
0
观察一下上面的算式,看看商的符号及其绝对值与除数、被除数有什么关系?
观察思考
到现在为止我们有了两个除法法则,那么两个法则是不是都可以用于解决两数相除呢?
1.两个法则都可以用来求两个有理数相除.
2.如果两数相除,能够整除的就选择法则二,不能够整除的就选择用法则一.
思考:
要点归纳:
例题讲授
例1
解:
=5
原式=+(15÷3)
(同号得正,绝对值相除)
(2)(-15)÷(-3)
牛刀小试
-3
9
0
-50
3
例3 化简下列分数
解:(1)原式
(2)原式
分数可以理解为分子除以分母.
例4 计算
解:(1)原式
(2)原式
方法归纳
(1)有理数除法化为有理数乘法,可利用有理数乘法运算律简化运算.
(2)乘除混合运算按从左到右的顺序进行计算,通常先把除法化为乘法,再确定积的符号,最后求出结果.
课堂检测
解:原式=( )×( )
=
(1)( )÷( )
解:原式=
解:原式=
1.有理数除法法则1:除以一个数等于乘以这个数的倒数.
有理数除法法则2:两个有理数相除,同号得正,异号得负,
并把绝对值相除.0除以任何非0的数都得0.
课堂小结
2.有理数乘除混合运算:按从左到右的顺序进行计算,通常先把除法化为乘法,再确定积的符号,最后求出结果.
作业布置
课本38页习题1.4 第4题,第12题
1.4.2 有理数的除法
复习回顾
1.有理数的乘法法则?
3.倒数的定义?
2.几个不为0的数相乘,积的符号法则?
4.你能很快地说出下列各数的倒数吗
原数 -5 0.2 0 -1
倒数
0为什么没有倒数?
-1
探究活动
怎样计算8÷(-4)呢?
8÷(-4)=
8×( )=
-2
于是
8×( )
8÷(-4)=
-2
因为(-2)×(-4)=8
所以8÷(-4)=-2
换其他数的除法进行类似讨论,是否仍有除以a(a≠0)可以转化为乘 ?
有理数除法法则
除以一个不等于0的数,等于乘这个数的倒数.
除号变乘号
除数变倒数作因数
通过上面的探究可得结论
表达式为: a ÷ b=a × (b≠0)
利用上面的除法法则计算下列各题:
(1) 27÷ (-9) =
(2) (-72)÷(-9)=
(3) 0÷ (-2) =
(4) 48÷ (-6) =
(5) (-18)÷6=
(7) (-27)÷(-9)=
-3
8
0
-8
-3
3
思考:从上面我们能发现商的符号有什么规律?
有理数除法法则的另一种说法:
两数相除,同号得 ,异号得 ,并把绝对值相 .0除以任何一个不等于0的数,都得 .
正
负
除
0
观察一下上面的算式,看看商的符号及其绝对值与除数、被除数有什么关系?
观察思考
到现在为止我们有了两个除法法则,那么两个法则是不是都可以用于解决两数相除呢?
1.两个法则都可以用来求两个有理数相除.
2.如果两数相除,能够整除的就选择法则二,不能够整除的就选择用法则一.
思考:
要点归纳:
例题讲授
例1
解:
=5
原式=+(15÷3)
(同号得正,绝对值相除)
(2)(-15)÷(-3)
牛刀小试
-3
9
0
-50
3
例3 化简下列分数
解:(1)原式
(2)原式
分数可以理解为分子除以分母.
例4 计算
解:(1)原式
(2)原式
方法归纳
(1)有理数除法化为有理数乘法,可利用有理数乘法运算律简化运算.
(2)乘除混合运算按从左到右的顺序进行计算,通常先把除法化为乘法,再确定积的符号,最后求出结果.
课堂检测
解:原式=( )×( )
=
(1)( )÷( )
解:原式=
解:原式=
1.有理数除法法则1:除以一个数等于乘以这个数的倒数.
有理数除法法则2:两个有理数相除,同号得正,异号得负,
并把绝对值相除.0除以任何非0的数都得0.
课堂小结
2.有理数乘除混合运算:按从左到右的顺序进行计算,通常先把除法化为乘法,再确定积的符号,最后求出结果.
作业布置
课本38页习题1.4 第4题,第12题
