2021-2022学年冀教版九年级数学下 册第29章直线与圆的位置关系复习与小结课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学下 册第29章直线与圆的位置关系复习与小结课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 11:29:44 | ||
图片预览





文档简介
(共21张PPT)
复习与小结
第二十九章 直线与圆的位置关系
冀教版九下
一、点与圆的位置关系
d:
1.利用d与r的数量关系确定点与圆的位置关系
圆心到点的距离
r:
圆的半径
点在圆内
d点在圆上
d=r
点在圆外
d>r
2.利用夹角与弦所对的圆周角比大小确定点与圆的位置关系
等于圆周角
大于圆周角
小于圆周角
点在圆内
点在圆上
点在圆外
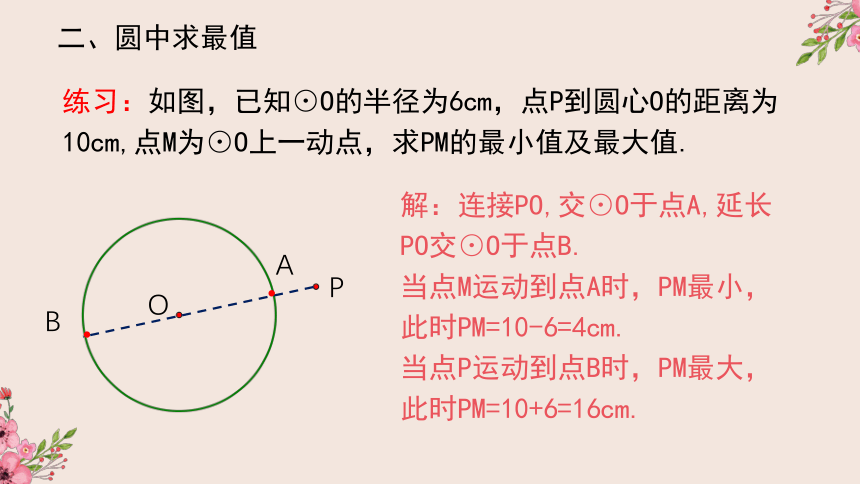
练习:如图,已知⊙O的半径为6cm,点P到圆心O的距离为10cm,点M为⊙O上一动点,求PM的最小值及最大值.
O
P
●
●
A
B
解:连接PO,交⊙O于点A,延长PO交⊙O于点B.
当点M运动到点A时,PM最小,此时PM=10-6=4cm.
当点P运动到点B时,PM最大,
此时PM=10+6=16cm.
二、圆中求最值
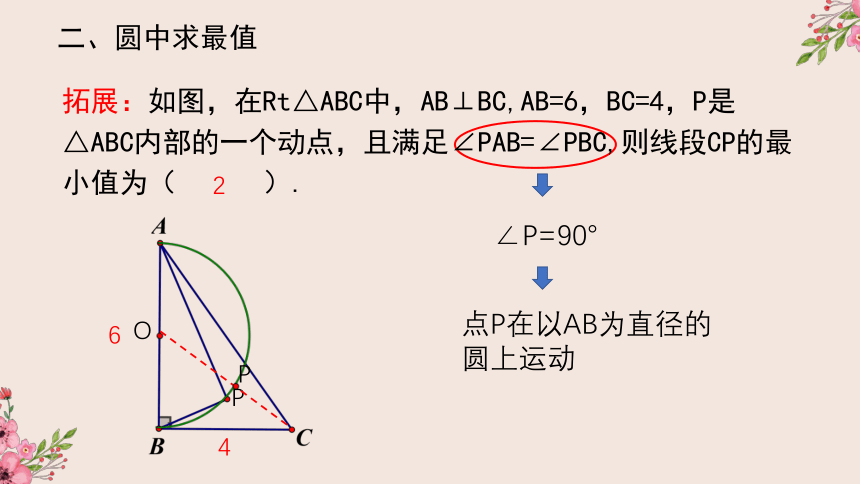
拓展:如图,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP的最小值为( ).
二、圆中求最值
6
4
P
P
O
2
∠P=90°
点P在以AB为直径的圆上运动
三、直线与圆的位置关系
d:
1.利用d与r的数量关系确定点与圆的位置关系
圆心到直线的距离
r:
圆的半径
相交
d相切
d=r
相离
d>r
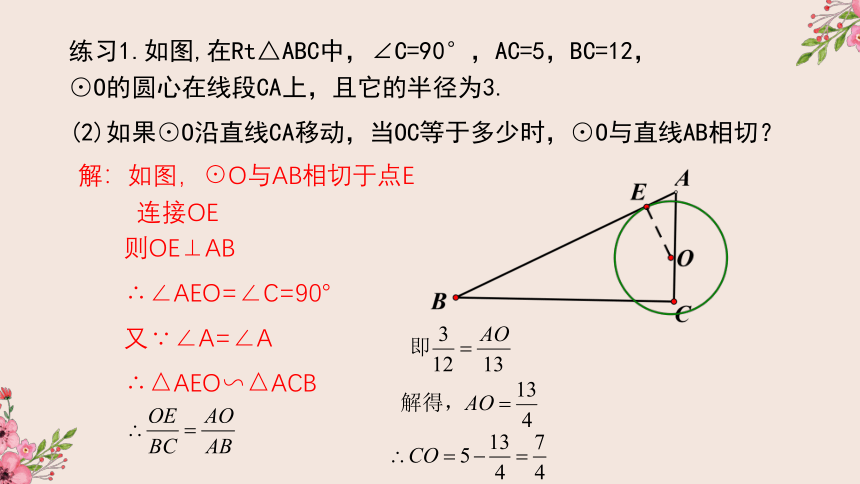
练习1.如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,⊙O的圆心在线段CA上,且它的半径为3.
(1)当点O与点C重合时,⊙O与直线AB具有怎样的位置关系?
解:过点C作CD⊥AB于点D
∴d>r
∴⊙O与直线AB相离
练习1.如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,⊙O的圆心在线段CA上,且它的半径为3.
(2)如果⊙O沿直线CA移动,当OC等于多少时,⊙O与直线AB相切?
解:如图,⊙O与AB相切于点E
连接OE
则OE⊥AB
∴∠AEO=∠C=90°
又∵∠A=∠A
∴△AEO∽△ACB
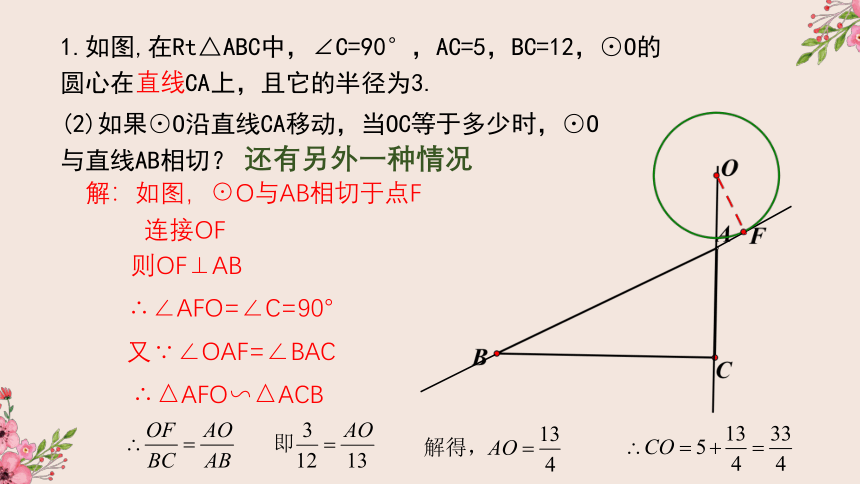
1.如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,⊙O的圆心在线段CA上,且它的半径为3.
(2)如果⊙O沿直线CA移动,当OC等于多少时,⊙O与直线AB相切?
解:如图,⊙O与AB相切于点F
连接OF
则OF⊥AB
∴∠AFO=∠C=90°
又∵∠OAF=∠BAC
∴△AFO∽△ACB
直线
还有另外一种情况
三、切线的判定与性质
1.切线的判定
①直线与圆有唯一公共点时,直线与圆相切.
②d=r时,直线与圆相切.
③直线经过半径的外端且与半径垂直时,直线与圆相切.
练习2.已知,如图,AB为⊙O的直径,C为⊙O上一点,点D在AB的延长线上,且∠DCB=∠A.
(1)求证:CD为⊙O的切线
∴AB为⊙O的直径
1
2
∴∠ACB=90°
即∠1+∠2=90°
∵OA=OC
∴∠A=∠1
∵∠DCB=∠A
∴∠DCB=∠1
∴∠2+∠DCB=90°
∴OC⊥CD
又∵OC为⊙O半径
∴CD为⊙O的切线
练习2.已知,如图,AB为⊙O的直径,C为⊙O上一点,点D在AB的延长线上,且∠DCB=∠A.
(2)若∠D=30°,BD=10cm,求⊙O的半径.
∴OD=2OC
∴OB=BD=10
在Rt△OCD中
∠D=30°
∵OD=OB+BD
∴⊙O的半径为10cm.
三、切线的判定与性质
2.切线的性质
①直线与圆相切时,d=r.
②圆的切线垂直于过切点的半径.
练习3.已知:如图,AB为⊙O的直径,C为⊙O上的一点上一点,AD和过点C的切线互相垂直,垂足为D.
(1)求证:AC平分∠DAB
想一想:
当已知条件中出现切线时,最常用到的辅助线时什么?
连接圆心和切点
得到垂直
练习3.已知:如图,AB为⊙O的直径,C为⊙O上的一点上一点,AD和过点C的切线互相垂直,垂足为D.
(1)求证:AC平分∠DAB
∵CD是⊙O的切线
∴OC⊥CD
∵AD⊥CD
∴OC∥AD
证明:连接OC
1
2
3
∴∠1=∠2
∵OA=OC
∴∠2=∠3
∴∠1=∠3
∴AC平分∠DAB
练习3.已知:如图,AB为⊙O的直径,C为⊙O上的一点上一点,AD和过点C的切线互相垂直,垂足为D.
(2)过点O作线段AC的垂线OE,垂足是E,
想一想:
(1)通常用什么知识求线段长?
勾股
相似
三角函数
面积
?
(2)结合图形以及已知中给出的数据,用哪一种比较合适?
相似
△ADC∽△AEO
∵OE⊥AC
由(1)得,∠EAC=∠BAC
∴△ADC∽△AEO
解:
又∵∠ADC=∠AEO=90°
四、切线长定理与旧知的链接
练习4.已知:如图,AB为⊙O的直径,E为⊙O外一点,EB,EC分别切⊙O于点B,C.求证:AC∥OE.
证明:∵EB,EC是⊙O的切线
∴EC=EB
∠CED=∠BED
∴ED⊥BC(三线合一)
∵AB为⊙O的直径
∴∠ACB=90°
∴AC∥OE
练习4.已知:如图,AB为⊙O的直径,E为⊙O外一点,EB,EC分别切⊙O于点B,C.求证:AC∥OE.
∵EB,EC是⊙O的切线
∴EC=EB
点E在BC的中垂线上
∵OC=OB
∴点O在BC的中垂线上
两点确定一条直线
∴OE垂直平分BC
证明:连接OC
∵AB为⊙O的直径
∴∠ACB=90°
∴AC∥OE
∴OE⊥BC
四、切线长定理与旧知的链接
练习4.已知:如图,AB为⊙O的直径,E为⊙O外一点,EB,EC分别切⊙O于点B,C.求证:AC∥OE.
证明:∵∠COB,∠A同对弧BC
∴∠COB=2∠A
∴∠COE=∠BOE
∴∠COB=2∠BOE
∴∠A=∠BOE
∴AC∥OE
∵EB,EC是⊙O的切线
四、切线长定理与旧知的链接
同学们再见
复习与小结
第二十九章 直线与圆的位置关系
冀教版九下
一、点与圆的位置关系
d:
1.利用d与r的数量关系确定点与圆的位置关系
圆心到点的距离
r:
圆的半径
点在圆内
d
d=r
点在圆外
d>r
2.利用夹角与弦所对的圆周角比大小确定点与圆的位置关系
等于圆周角
大于圆周角
小于圆周角
点在圆内
点在圆上
点在圆外
练习:如图,已知⊙O的半径为6cm,点P到圆心O的距离为10cm,点M为⊙O上一动点,求PM的最小值及最大值.
O
P
●
●
A
B
解:连接PO,交⊙O于点A,延长PO交⊙O于点B.
当点M运动到点A时,PM最小,此时PM=10-6=4cm.
当点P运动到点B时,PM最大,
此时PM=10+6=16cm.
二、圆中求最值
拓展:如图,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP的最小值为( ).
二、圆中求最值
6
4
P
P
O
2
∠P=90°
点P在以AB为直径的圆上运动
三、直线与圆的位置关系
d:
1.利用d与r的数量关系确定点与圆的位置关系
圆心到直线的距离
r:
圆的半径
相交
d
d=r
相离
d>r
练习1.如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,⊙O的圆心在线段CA上,且它的半径为3.
(1)当点O与点C重合时,⊙O与直线AB具有怎样的位置关系?
解:过点C作CD⊥AB于点D
∴d>r
∴⊙O与直线AB相离
练习1.如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,⊙O的圆心在线段CA上,且它的半径为3.
(2)如果⊙O沿直线CA移动,当OC等于多少时,⊙O与直线AB相切?
解:如图,⊙O与AB相切于点E
连接OE
则OE⊥AB
∴∠AEO=∠C=90°
又∵∠A=∠A
∴△AEO∽△ACB
1.如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,⊙O的圆心在线段CA上,且它的半径为3.
(2)如果⊙O沿直线CA移动,当OC等于多少时,⊙O与直线AB相切?
解:如图,⊙O与AB相切于点F
连接OF
则OF⊥AB
∴∠AFO=∠C=90°
又∵∠OAF=∠BAC
∴△AFO∽△ACB
直线
还有另外一种情况
三、切线的判定与性质
1.切线的判定
①直线与圆有唯一公共点时,直线与圆相切.
②d=r时,直线与圆相切.
③直线经过半径的外端且与半径垂直时,直线与圆相切.
练习2.已知,如图,AB为⊙O的直径,C为⊙O上一点,点D在AB的延长线上,且∠DCB=∠A.
(1)求证:CD为⊙O的切线
∴AB为⊙O的直径
1
2
∴∠ACB=90°
即∠1+∠2=90°
∵OA=OC
∴∠A=∠1
∵∠DCB=∠A
∴∠DCB=∠1
∴∠2+∠DCB=90°
∴OC⊥CD
又∵OC为⊙O半径
∴CD为⊙O的切线
练习2.已知,如图,AB为⊙O的直径,C为⊙O上一点,点D在AB的延长线上,且∠DCB=∠A.
(2)若∠D=30°,BD=10cm,求⊙O的半径.
∴OD=2OC
∴OB=BD=10
在Rt△OCD中
∠D=30°
∵OD=OB+BD
∴⊙O的半径为10cm.
三、切线的判定与性质
2.切线的性质
①直线与圆相切时,d=r.
②圆的切线垂直于过切点的半径.
练习3.已知:如图,AB为⊙O的直径,C为⊙O上的一点上一点,AD和过点C的切线互相垂直,垂足为D.
(1)求证:AC平分∠DAB
想一想:
当已知条件中出现切线时,最常用到的辅助线时什么?
连接圆心和切点
得到垂直
练习3.已知:如图,AB为⊙O的直径,C为⊙O上的一点上一点,AD和过点C的切线互相垂直,垂足为D.
(1)求证:AC平分∠DAB
∵CD是⊙O的切线
∴OC⊥CD
∵AD⊥CD
∴OC∥AD
证明:连接OC
1
2
3
∴∠1=∠2
∵OA=OC
∴∠2=∠3
∴∠1=∠3
∴AC平分∠DAB
练习3.已知:如图,AB为⊙O的直径,C为⊙O上的一点上一点,AD和过点C的切线互相垂直,垂足为D.
(2)过点O作线段AC的垂线OE,垂足是E,
想一想:
(1)通常用什么知识求线段长?
勾股
相似
三角函数
面积
?
(2)结合图形以及已知中给出的数据,用哪一种比较合适?
相似
△ADC∽△AEO
∵OE⊥AC
由(1)得,∠EAC=∠BAC
∴△ADC∽△AEO
解:
又∵∠ADC=∠AEO=90°
四、切线长定理与旧知的链接
练习4.已知:如图,AB为⊙O的直径,E为⊙O外一点,EB,EC分别切⊙O于点B,C.求证:AC∥OE.
证明:∵EB,EC是⊙O的切线
∴EC=EB
∠CED=∠BED
∴ED⊥BC(三线合一)
∵AB为⊙O的直径
∴∠ACB=90°
∴AC∥OE
练习4.已知:如图,AB为⊙O的直径,E为⊙O外一点,EB,EC分别切⊙O于点B,C.求证:AC∥OE.
∵EB,EC是⊙O的切线
∴EC=EB
点E在BC的中垂线上
∵OC=OB
∴点O在BC的中垂线上
两点确定一条直线
∴OE垂直平分BC
证明:连接OC
∵AB为⊙O的直径
∴∠ACB=90°
∴AC∥OE
∴OE⊥BC
四、切线长定理与旧知的链接
练习4.已知:如图,AB为⊙O的直径,E为⊙O外一点,EB,EC分别切⊙O于点B,C.求证:AC∥OE.
证明:∵∠COB,∠A同对弧BC
∴∠COB=2∠A
∴∠COE=∠BOE
∴∠COB=2∠BOE
∴∠A=∠BOE
∴AC∥OE
∵EB,EC是⊙O的切线
四、切线长定理与旧知的链接
同学们再见
