2021--2022学年华东师大版九年级数学上册25.2.2 频率与概率 课件(共15张PPT)
文档属性
| 名称 | 2021--2022学年华东师大版九年级数学上册25.2.2 频率与概率 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 12:10:27 | ||
图片预览




文档简介
(共15张PPT)
检测互评
自学互助
质疑互究
展示互导
总结提升
第25章 随机事件的概率
25.2.2频率与概率
空白演示
在此输入您的封面副标题
频率=
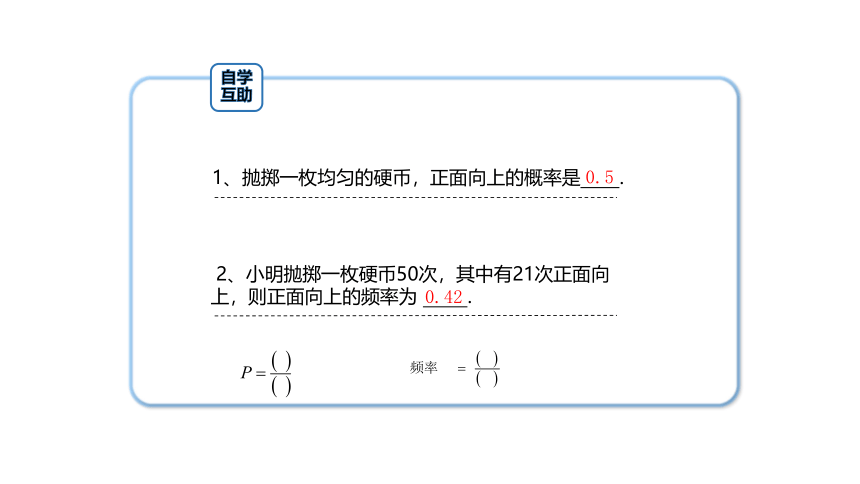
自学互助
1、抛掷一枚均匀的硬币,正面向上的概率是 .
2、小明抛掷一枚硬币50次,其中有21次正面向上,则正面向上的频率为 .
0.5
0.42
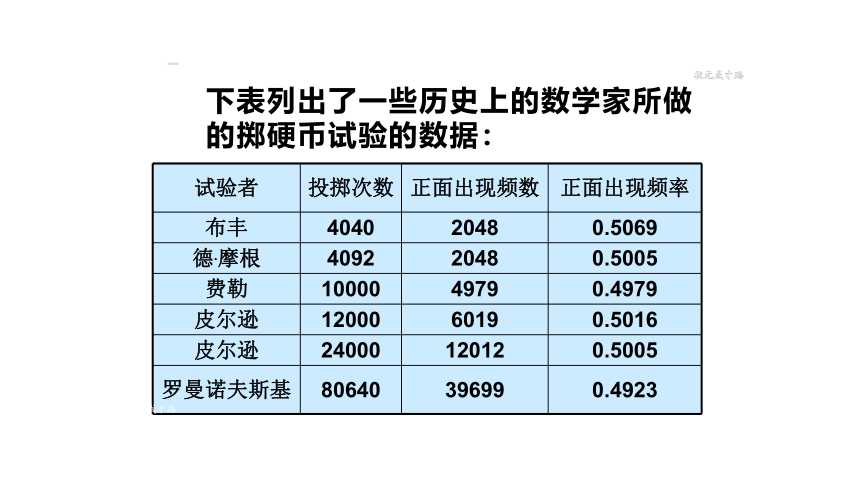
下表列出了一些历史上的数学家所做的掷硬币试验的数据:
试验者 投掷次数 正面出现频数 正面出现频率
布丰 4040 2048 0.5069
德.摩根 4092 2048 0.5005
费勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
罗曼诺夫斯基 80640 39699 0.4923
做一做:小明、小凡和小颖都想去看周末电影,但只有一张电影票.三人决定一起做游戏,谁获胜谁就去看电影.游戏规则如下:
连续抛掷两枚均匀的硬币,如果两枚正面朝上,则小明获胜;如果两枚反面朝上,则小颖获胜;如果一枚正面朝上、一枚反面朝上,小凡获胜.
小明
小颖
小凡
质疑互究
“掷两枚硬币”所有结果如下:
正正
正反
反正
反反
①
②
①
②
①
②
①
②
P(小明获胜)=
P(小颖胜)=
∴这个游戏不公平.
解:
P(小凡胜)=
开始
第一枚
第二枚
所有可能出现的结果
(正、正)
(正、反)
(反、正)
(反、反)
还有别的方法吗?
问题引入
画树状图:按事件发生的次序,列出事件可能出现的结果.
第一枚硬币 第二枚硬币 所有可能出现的结果
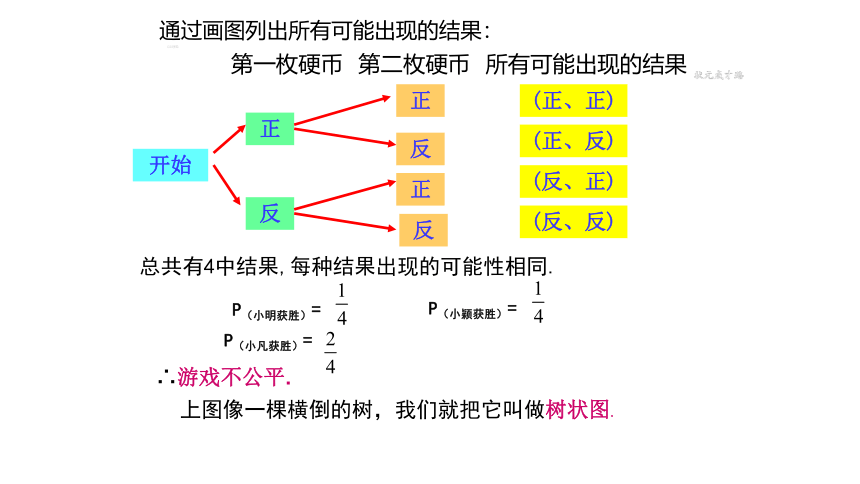
通过画图列出所有可能出现的结果:
开始
正
反
正
反
正
反
(正、正)
(正、反)
(反、正)
(反、反)
总共有4中结果,每种结果出现的可能性相同.
P(小明获胜)=
P(小颖获胜)=
P(小凡获胜)=
上图像一棵横倒的树,我们就把它叫做树状图.
∴游戏不公平.
①
①
①
②
②
①
①
②
②
②
①
②
第1枚硬币
第
2
枚硬币
反
正
正
反
正
正
反
正
正
反
反
反
还可以用列表法求概率
列表如下:
(正、正)
(反、正)
(正、反)
(反、反)
第二枚硬币
第一枚硬币
正
反
正
反
总共有4中结果,每种结果出现的可能性相同.
叫列表法
利用树状图或表格,我们可以不重复、不遗漏地列出所有可能性相同的结果,从而比较方便地求出我们关注事件发生的概率.
结论
P(小明获胜)=
P(小颖获胜)=
P(小凡获胜)=
∴游戏不公平.
“配紫色”游戏
游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
红
白
黄
蓝
绿
A盘
B盘
展示互导
解:所有可能出现的结果如下:
“配紫色”游戏
第二个 转盘 第一个 转盘
黄
蓝
绿
红
(红,黄)
(红,蓝)
(红,绿)
白
(白,黄)
(白,蓝)
(白,绿)
红
白
黄
蓝
绿
A盘
B盘
总共有6种结果,每种结果出现的可能性相同,而可以配成紫色的结果有1种:(红,蓝),因此P(游戏者获胜)=1/6。
1200
红
红
蓝
蓝
用如图所示的转盘进行“配紫色”游戏.
小颖制作了下图,并据此求出游戏者获胜的 概率是1/2.
“配紫色”游戏的变异
对此你有什么评论?
开始
红
蓝
红
蓝
红
蓝
(红,红)
(红,蓝)
(蓝,红)
(蓝,蓝)
“配紫色”游戏的变异
解:所有可能出现的结果如下:
1200
红1
红
蓝
蓝
红2
(蓝,蓝)
(蓝,红)
蓝色
(红2,蓝)
(红2,红)
红色2
(红1,蓝)
(红1,红)
红色1
蓝色
红色
总共有6种结果,每种结果出现的可能性相同,而可以配成紫色的结果有3种:(红1,蓝)(红2,蓝),(蓝,红)因此P(游戏者获胜)=1/2。
1、将一枚图钉随意向上抛起,求图钉落定后钉尖触地的概率.
虽然一枚图钉被抛起后落定的结果只有两种:“钉尖朝上”“钉尖触地”,但由于图钉的形状比较特殊,我们无法用分析的方法预测P(钉尖朝上)与P(钉尖触地)的数值,因此,只能让重复试验来帮忙.
46.0%
四、检测互评。
1、在一个不透明的口袋中装有4个红球和若干个白球,他们除颜色外其他完全相同。通过多次摸球实验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )
A、6个 B、15个 C、13个 D、12个
2、某鱼塘里养了100条鲤鱼、若干条草鱼和50条罗非鱼,通过多次捕捞实验后发现,捕捞到草鱼的频率稳定在0.4左右,可估计该鱼塘中草鱼的数量为 .
检测互评
自学互助
质疑互究
展示互导
总结提升
第25章 随机事件的概率
25.2.2频率与概率
空白演示
在此输入您的封面副标题
频率=
自学互助
1、抛掷一枚均匀的硬币,正面向上的概率是 .
2、小明抛掷一枚硬币50次,其中有21次正面向上,则正面向上的频率为 .
0.5
0.42
下表列出了一些历史上的数学家所做的掷硬币试验的数据:
试验者 投掷次数 正面出现频数 正面出现频率
布丰 4040 2048 0.5069
德.摩根 4092 2048 0.5005
费勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
罗曼诺夫斯基 80640 39699 0.4923
做一做:小明、小凡和小颖都想去看周末电影,但只有一张电影票.三人决定一起做游戏,谁获胜谁就去看电影.游戏规则如下:
连续抛掷两枚均匀的硬币,如果两枚正面朝上,则小明获胜;如果两枚反面朝上,则小颖获胜;如果一枚正面朝上、一枚反面朝上,小凡获胜.
小明
小颖
小凡
质疑互究
“掷两枚硬币”所有结果如下:
正正
正反
反正
反反
①
②
①
②
①
②
①
②
P(小明获胜)=
P(小颖胜)=
∴这个游戏不公平.
解:
P(小凡胜)=
开始
第一枚
第二枚
所有可能出现的结果
(正、正)
(正、反)
(反、正)
(反、反)
还有别的方法吗?
问题引入
画树状图:按事件发生的次序,列出事件可能出现的结果.
第一枚硬币 第二枚硬币 所有可能出现的结果
通过画图列出所有可能出现的结果:
开始
正
反
正
反
正
反
(正、正)
(正、反)
(反、正)
(反、反)
总共有4中结果,每种结果出现的可能性相同.
P(小明获胜)=
P(小颖获胜)=
P(小凡获胜)=
上图像一棵横倒的树,我们就把它叫做树状图.
∴游戏不公平.
①
①
①
②
②
①
①
②
②
②
①
②
第1枚硬币
第
2
枚硬币
反
正
正
反
正
正
反
正
正
反
反
反
还可以用列表法求概率
列表如下:
(正、正)
(反、正)
(正、反)
(反、反)
第二枚硬币
第一枚硬币
正
反
正
反
总共有4中结果,每种结果出现的可能性相同.
叫列表法
利用树状图或表格,我们可以不重复、不遗漏地列出所有可能性相同的结果,从而比较方便地求出我们关注事件发生的概率.
结论
P(小明获胜)=
P(小颖获胜)=
P(小凡获胜)=
∴游戏不公平.
“配紫色”游戏
游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
红
白
黄
蓝
绿
A盘
B盘
展示互导
解:所有可能出现的结果如下:
“配紫色”游戏
第二个 转盘 第一个 转盘
黄
蓝
绿
红
(红,黄)
(红,蓝)
(红,绿)
白
(白,黄)
(白,蓝)
(白,绿)
红
白
黄
蓝
绿
A盘
B盘
总共有6种结果,每种结果出现的可能性相同,而可以配成紫色的结果有1种:(红,蓝),因此P(游戏者获胜)=1/6。
1200
红
红
蓝
蓝
用如图所示的转盘进行“配紫色”游戏.
小颖制作了下图,并据此求出游戏者获胜的 概率是1/2.
“配紫色”游戏的变异
对此你有什么评论?
开始
红
蓝
红
蓝
红
蓝
(红,红)
(红,蓝)
(蓝,红)
(蓝,蓝)
“配紫色”游戏的变异
解:所有可能出现的结果如下:
1200
红1
红
蓝
蓝
红2
(蓝,蓝)
(蓝,红)
蓝色
(红2,蓝)
(红2,红)
红色2
(红1,蓝)
(红1,红)
红色1
蓝色
红色
总共有6种结果,每种结果出现的可能性相同,而可以配成紫色的结果有3种:(红1,蓝)(红2,蓝),(蓝,红)因此P(游戏者获胜)=1/2。
1、将一枚图钉随意向上抛起,求图钉落定后钉尖触地的概率.
虽然一枚图钉被抛起后落定的结果只有两种:“钉尖朝上”“钉尖触地”,但由于图钉的形状比较特殊,我们无法用分析的方法预测P(钉尖朝上)与P(钉尖触地)的数值,因此,只能让重复试验来帮忙.
46.0%
四、检测互评。
1、在一个不透明的口袋中装有4个红球和若干个白球,他们除颜色外其他完全相同。通过多次摸球实验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )
A、6个 B、15个 C、13个 D、12个
2、某鱼塘里养了100条鲤鱼、若干条草鱼和50条罗非鱼,通过多次捕捞实验后发现,捕捞到草鱼的频率稳定在0.4左右,可估计该鱼塘中草鱼的数量为 .
