点与圆的位置关系(2)

(共18张PPT)
24.2与圆有关的位置关系
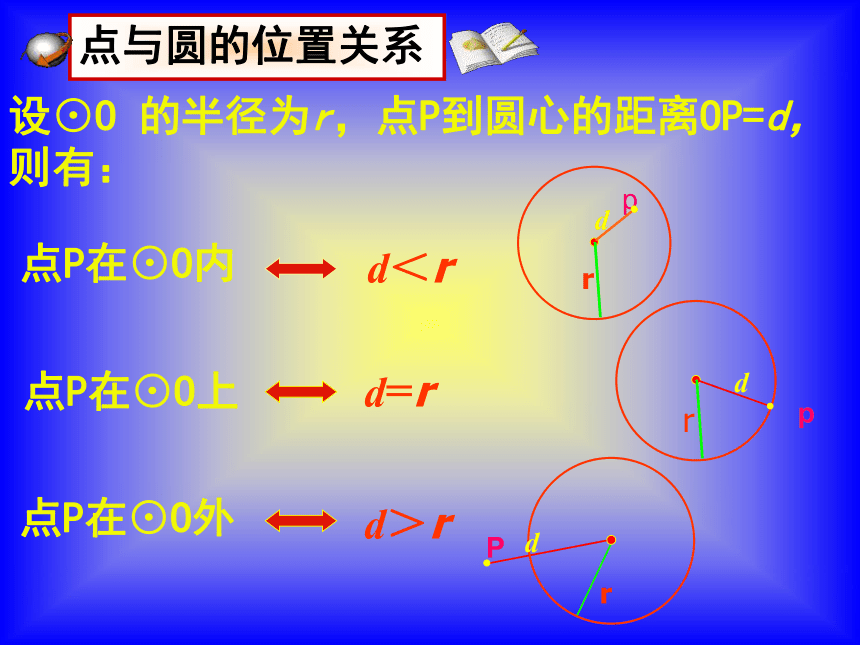
设⊙O 的半径为r，点P到圆心的距离OP=d，则有：
点P在⊙O内
点P在⊙O上
点P在⊙O外
点与圆的位置关系
d＜r
d=r
d＞r
r
p
d
p
r
d
P
r
d
回顾与思考
确定圆的条件:圆心和半径
两点确定一条直线.对于圆来说,是否也有几点确定的问题呢
1、平面上有一点A，经过已知A点的圆有几个？圆心在哪里？
探究与实践
●O
●A
●O
●O
●O
●O
无数个，圆心为点A以外任意一点，半径为这点与点A的距离
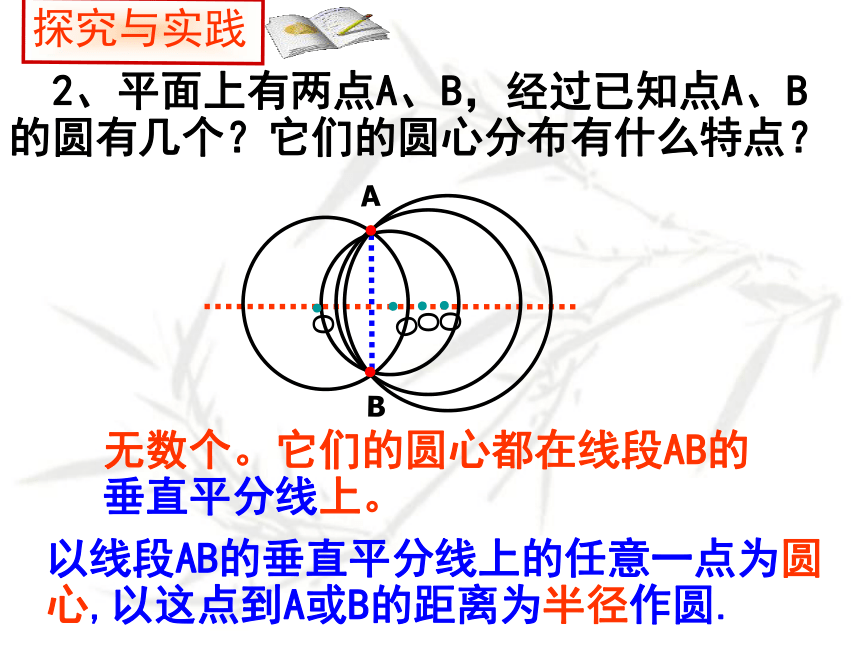
2、平面上有两点A、B，经过已知点A、B的圆有几个？它们的圆心分布有什么特点？
探究与实践
●O
● O
●O
●O
A
B
以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
无数个。它们的圆心都在线段AB的垂直平分线上。
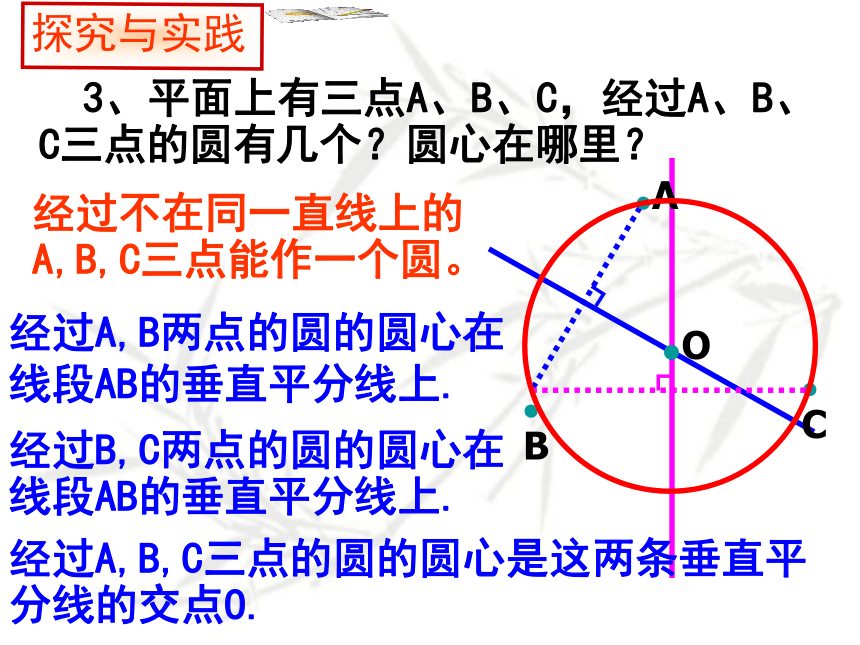
3、平面上有三点A、B、C，经过A、B、C三点的圆有几个？圆心在哪里？
探究与实践
┓
●B
●C
经过B,C两点的圆的圆心在线段AB的垂直平分线上.
┏
●A
经过A,B,C三点的圆的圆心是这两条垂直平分线的交点O.
●O
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
经过不在同一直线上的
A,B,C三点能作一个圆。
探究与实践
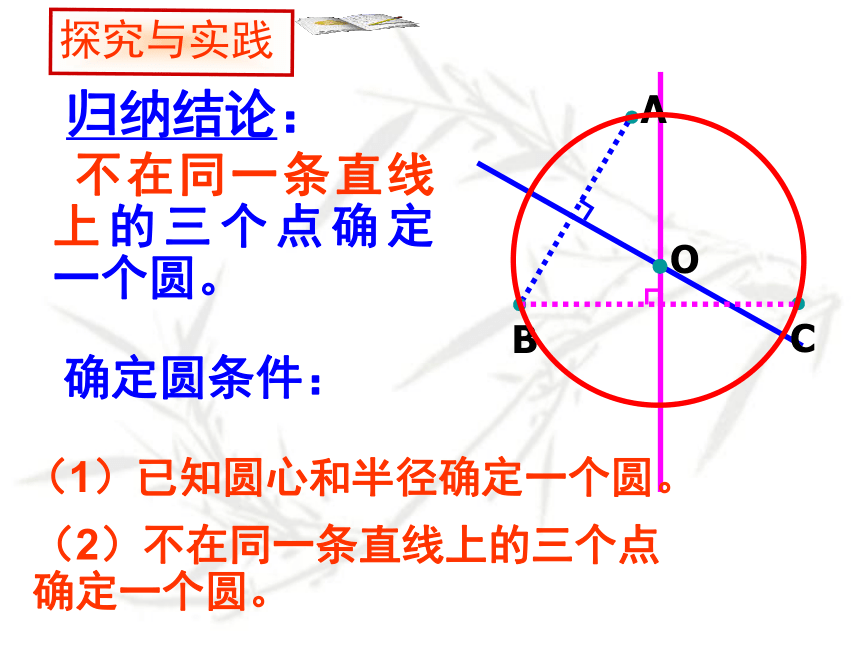
不在同一条直线上的三个点确定一个圆。
┓
●B
●C
┏
●A
●O
归纳结论：
确定圆条件：
（2）不在同一条直线上的三个点
确定一个圆。
（1）已知圆心和半径确定一个圆。
经过三角形三个顶点可以画一个圆，并且只能画一个．
一个三角形的外接圆有几个？
一个圆的内接三角形有几个？
经过三角形三个顶点的圆叫做三角形的外接圆。
三角形的外心就是三角形三条边的垂直平分线的交点，它到三角形三个顶点的距离相等。
这个三角形叫做这个圆的内接三角形。
三角形外接圆的圆心叫做这个三角形的外心。
●O
A
B
C
有关概念
分别画一个锐角三角形、直角三角形和钝角三角形，再画出它们的外接圆，观察并叙述各三角形与它的外心的位置关系.
做一做
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
练一练
1、判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆( ).
(2)任意一个圆有且只有一个内接三角形( )
(3)经过三点一定可以确定一个圆( )
(4)三角形的外心到三角形各顶点的距离
相等( )
2、若一个三角形的外心在一边上，则此三角形的形状为( )
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等腰三角形
√
×
×
√
B
E
D
C
B
A
如图，已知等边△ABC中，AB=6cm，求它的外接圆半径。
典型例题1
O
如图，已知Rt△ABC中，∠C=900
若 AC=12cm，BC=5cm，
求的外接圆半径。
C
B
A
O
O
如图，等腰△ABC中，
，求外接圆的半径。
A
D
C
B
思考：经过同一直线上的A,B,C三点能作出一个圆吗？
探究与实践
A
B
C
l1
l2
P
从命题结论的反面出发，假设命题的结论不成立，由此经过推理得出矛盾，由矛盾断定所作假设不正确，从而得到原命题成立。这种方法叫反证法。
反证法：
求证：在一个三角形中，至少有一个内角大于或等于600 .
典型例题2
已知：△ABC
求证：△ABC中至少有一个内角大于或等于600 .
B
C
A
即△ABC中至少有一个内角大于或等于60°.
证明：假设△ABC的三个内角都小于60°,
即∠A＜60°,∠B＜60°,∠C＜60°,
∴∠A＋∠B＋∠C＜180°,
这与“三角形的内角和等于180°”相矛盾，所以假设不成立，原命题的结论成立。
用反证法证明：一个三角形中不能有两个直角。
练一练
已知：△ABC
求证：△ABC中不能有两个直角
B
C
A
即△ABC中不能有两个直角。
证明：假设△ABC中有两个直角,
即∠A＝90°,∠B＝90°,
∴∠A＋∠B＋∠C＞180°,
这与“三角形的内角和等于180°”相矛盾，所以假设不成立，原命题的结论成立。
这节课你学到了哪些知识？有什么感想
回顾与思考
用数量关系判断点和圆的位置关系。
不在同一直线上的三点确定一个圆。
求解特殊三角形直角三角形、等边三角形、等腰三角形的外接圆半径。
在求解等腰三角形外接圆半径时，运用了方程的思想，希望同学们能够掌握这种方法，领会其思想。
从命题结论的反面出发，假设命题的结论不成立，由此经过推理得出矛盾，由矛盾断定所作假设不正确，从而得到原命题成立。这种方法叫反证法。