24.1.3 弧、弦、圆心角的关系
文档属性
| 名称 | 24.1.3 弧、弦、圆心角的关系 |  | |
| 格式 | zip | ||
| 文件大小 | 207.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-29 15:25:55 | ||
图片预览


文档简介
(共23张PPT)
圆是轴对称图形.圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
圆也是中心对称图形.
它的对称中心就是圆心.
圆是轴对称图形吗?如果是,它的对称轴是什么 你能找到多少条对称轴?
圆是中心对称图形吗?
●O
●O
A
B
一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.
这是圆特有的一个性质:圆的旋转不变性
·
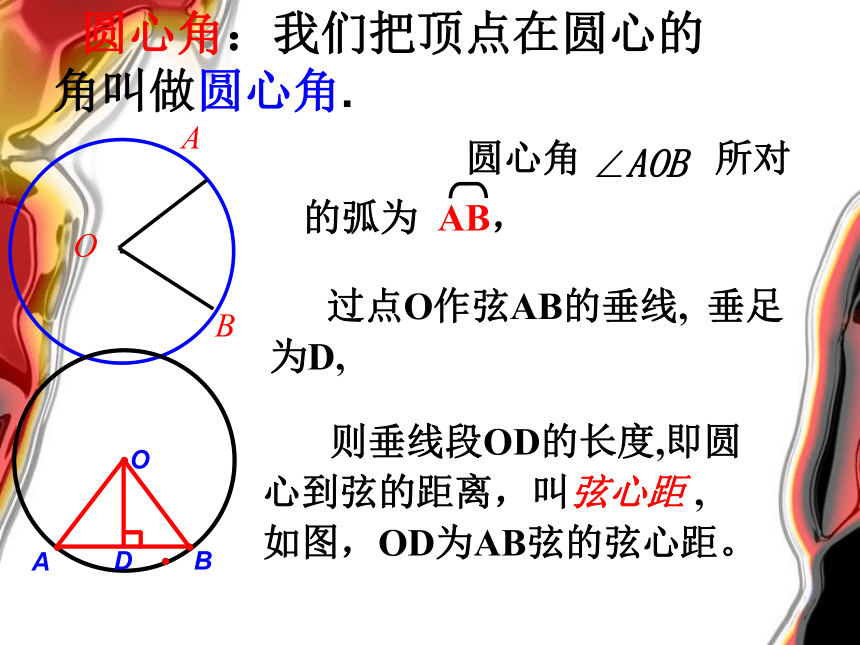
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
圆心角 所对
的弧为 AB,
过点O作弦AB的垂线, 垂足
为D,
则垂线段OD的长度,即圆心到弦的距离,叫弦心距 ,
如图,OD为AB弦的弦心距。
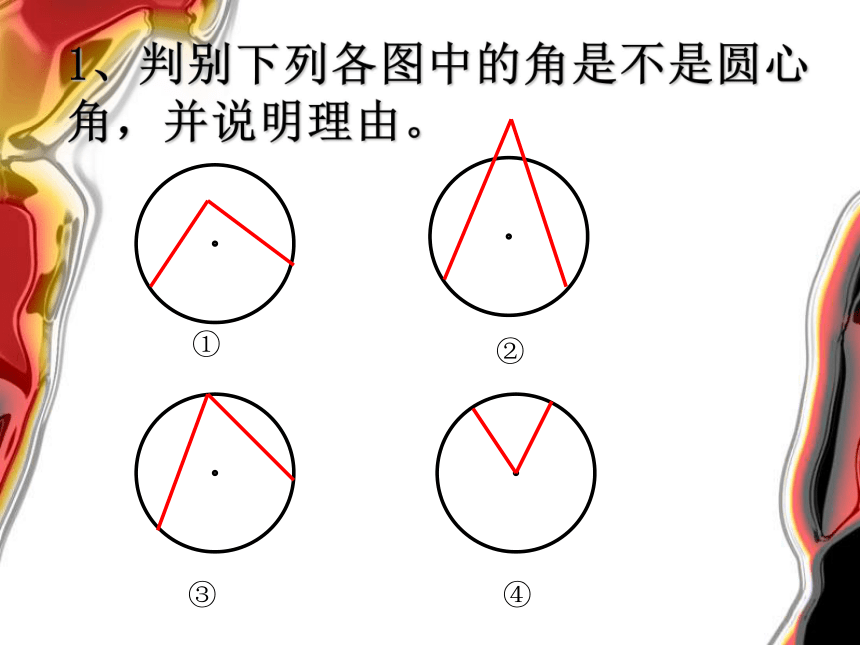
1、判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
·
O
A
B
·
O
A
B
A′
B′
A′
B′
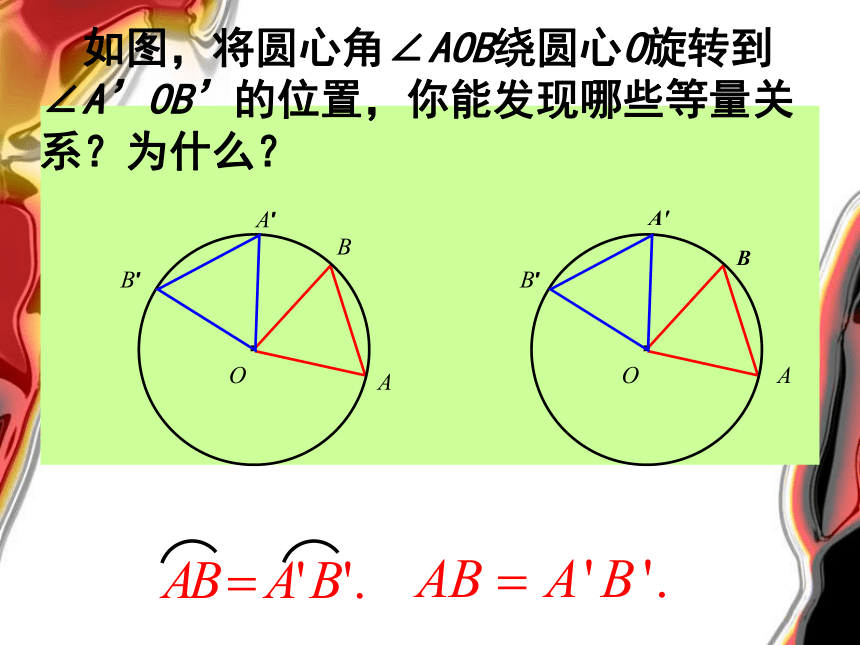
如图,将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置,你能发现哪些等量关系?为什么?
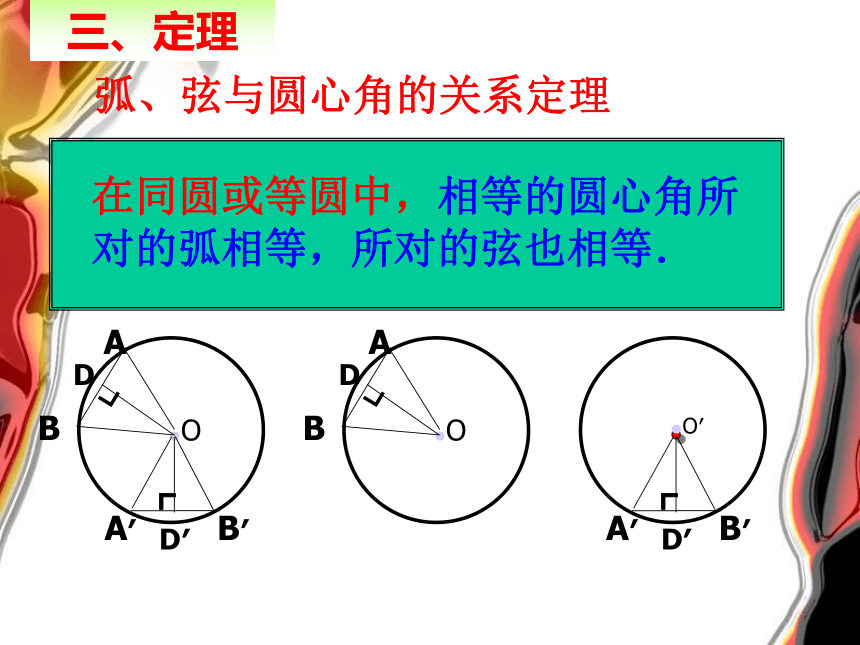
弧、弦与圆心角的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
三、定理
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
┓
D
●O′
A′
B′
D′
┏
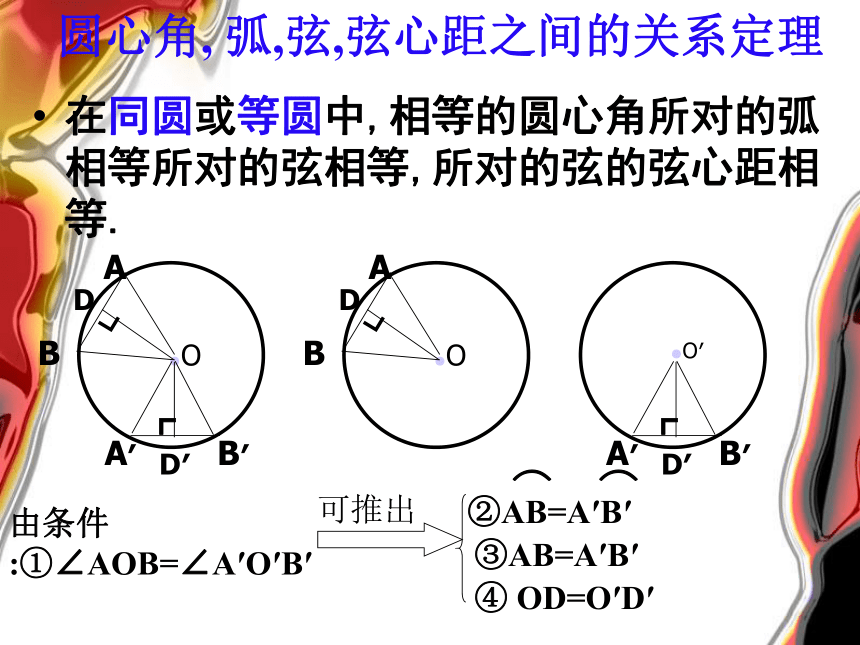
圆心角, 弧,弦,弦心距之间的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
┓
D
●O′
A′
B′
D′
┏
由条件:①∠AOB=∠A′O′B′
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
可推出
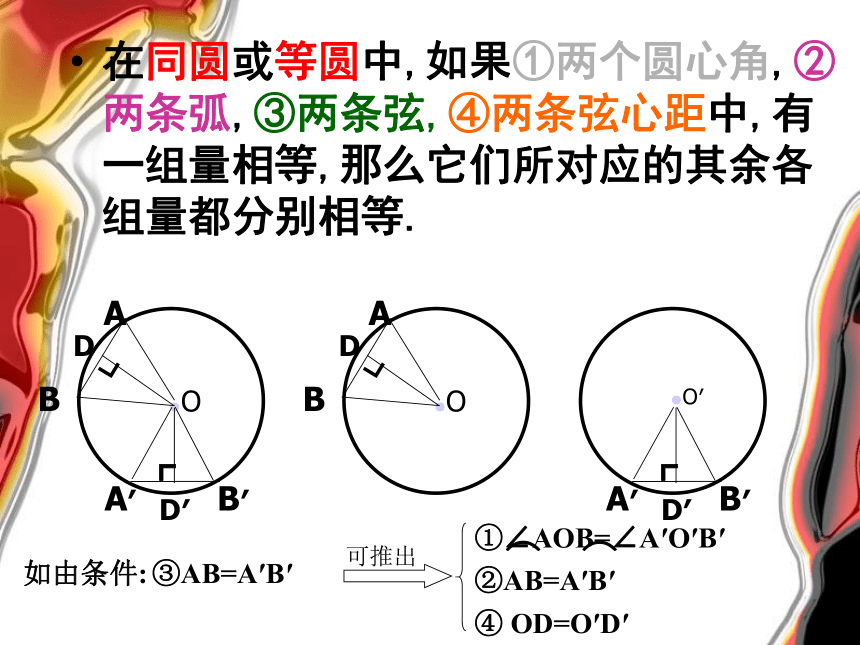
在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
┓
D
●O′
A′
B′
D′
┏
如由条件:
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
可推出
①∠AOB=∠A′O′B′
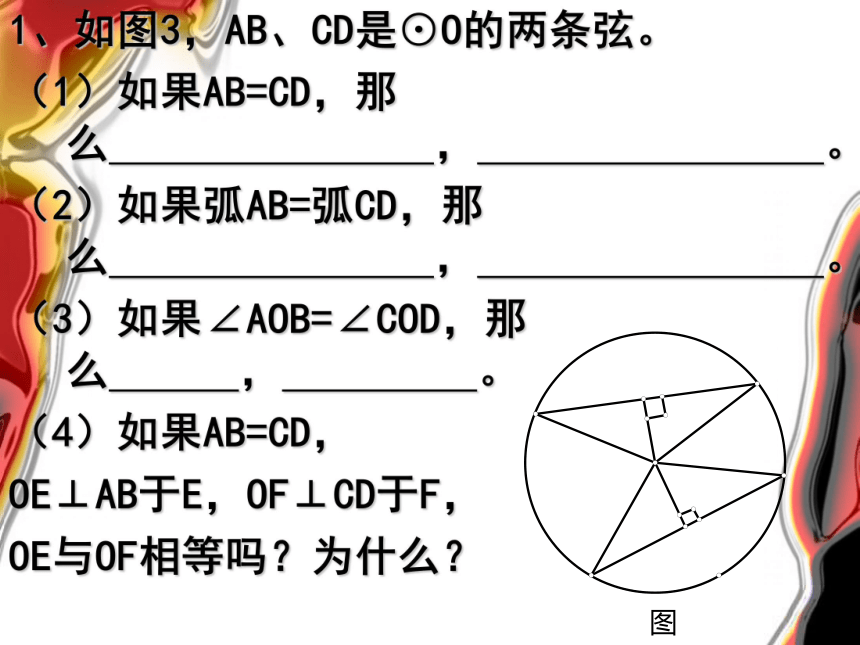
1、如图3,AB、CD是⊙O的两条弦。
(1)如果AB=CD,那么 , 。
(2)如果弧AB=弧CD,那么 , 。
(3)如果∠AOB=∠COD,那么 , 。
(4)如果AB=CD,
OE⊥AB于E,OF⊥CD于F,
OE与OF相等吗?为什么?
4、在⊙O中,一条弦AB所对的劣弧为圆周的1/4,则弦AB所对的圆心角为 。
5、在半径为2的⊙O中,圆心O到弦AB的距离为1,则弦AB所对的圆心角的度数为 。
6、如图5,在⊙O中
弧AB=弧AC,∠C=75°,
求∠A的度数。
基础训练
例题解析
证明: ∵弧AB=弧AC
∴AB=AC,△ABC是等腰三角形
又 ∠ACB=60°
∴△ABC是等边三角形,AB=BC=CA
∴∠AOB=∠BOC=∠AOC
例1 如图1,在⊙O中,弧AB=弧AC,∠ACB=60°,
求证∠AOB=∠BOC=∠AOC。
2、如图4,AB是⊙O的直径,弧BC=弧CD=弧DE,∠COD=35°,求∠AOE的度数。
基础训练
3、如图,已知AD=BC、求证AB=CD
. O
A
B
C
D
变式:如图,如果弧AB=弧CD,
求证:AD=CB
4、如图,已知AB、CD是⊙O中互相垂直的两条直径,又两条弦AE、CF垂直相交与点G,试证明:AE=CF
P
. O
A
B
C
D
┌
┐
G
E
F
如图7所示,CD为⊙O的弦,在CD上取CE=DF,连结OE、OF,并延长交⊙O于点A、B。
(1)试判断△OEF的形状,并说明理由;
(2)求证:弧AC=弧BD
拓展训练
例题解析
例2 已知:如图2,AB、CD是⊙O的弦,且AB与CD不平行,M、N分别是AB、CD的中点,AB=CD,那么∠AMN与∠CNM的大小关系是什么?为什么?
解:连结OM、ON,
∵M、N分别为弦AB、CD的中点,
∴∠AMO=∠CNO=90°
∵ AB=CD
∴ OM=ON
∴∠OMN=∠CNM
∴∠AMN=∠CNM
D
O
B
A
C
M
N
3、如图,点O是∠EPF角平分线上的一点,以O为圆心的圆和角的两边分别交于点A、B和C、D。
求证:AB= CD。
O
A
B
P
C
D
E
F
M
N
基础练习
如图,⊙O中两条相等的弦AB、CD分别延长到E、F,使BE= DF。
求证:EF的垂直平分线必经过点O。
O
A
B
C
D
E
F
M
N
课后思考题
A
B
O
M
N
P
如图,MN为圆O的直径,已知点A是半圆上个三等分点,点B是弧AN的中点,点P是半径ON上的动点,若圆O的半径为1,求AP+BP的最小值.
如图已知弧AD所对的圆心角为90度,点B,C将弧AD三等分,弦AD与半径0B,OC相交于点E,F,
求证:AE=BC=FD
D
C
A
B
O
八、作业
1、教材87-88页
2,3, 10,12
圆是轴对称图形.圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
圆也是中心对称图形.
它的对称中心就是圆心.
圆是轴对称图形吗?如果是,它的对称轴是什么 你能找到多少条对称轴?
圆是中心对称图形吗?
●O
●O
A
B
一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.
这是圆特有的一个性质:圆的旋转不变性
·
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
圆心角 所对
的弧为 AB,
过点O作弦AB的垂线, 垂足
为D,
则垂线段OD的长度,即圆心到弦的距离,叫弦心距 ,
如图,OD为AB弦的弦心距。
1、判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
·
O
A
B
·
O
A
B
A′
B′
A′
B′
如图,将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置,你能发现哪些等量关系?为什么?
弧、弦与圆心角的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
三、定理
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
┓
D
●O′
A′
B′
D′
┏
圆心角, 弧,弦,弦心距之间的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
┓
D
●O′
A′
B′
D′
┏
由条件:①∠AOB=∠A′O′B′
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
可推出
在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
┓
D
●O′
A′
B′
D′
┏
如由条件:
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
可推出
①∠AOB=∠A′O′B′
1、如图3,AB、CD是⊙O的两条弦。
(1)如果AB=CD,那么 , 。
(2)如果弧AB=弧CD,那么 , 。
(3)如果∠AOB=∠COD,那么 , 。
(4)如果AB=CD,
OE⊥AB于E,OF⊥CD于F,
OE与OF相等吗?为什么?
4、在⊙O中,一条弦AB所对的劣弧为圆周的1/4,则弦AB所对的圆心角为 。
5、在半径为2的⊙O中,圆心O到弦AB的距离为1,则弦AB所对的圆心角的度数为 。
6、如图5,在⊙O中
弧AB=弧AC,∠C=75°,
求∠A的度数。
基础训练
例题解析
证明: ∵弧AB=弧AC
∴AB=AC,△ABC是等腰三角形
又 ∠ACB=60°
∴△ABC是等边三角形,AB=BC=CA
∴∠AOB=∠BOC=∠AOC
例1 如图1,在⊙O中,弧AB=弧AC,∠ACB=60°,
求证∠AOB=∠BOC=∠AOC。
2、如图4,AB是⊙O的直径,弧BC=弧CD=弧DE,∠COD=35°,求∠AOE的度数。
基础训练
3、如图,已知AD=BC、求证AB=CD
. O
A
B
C
D
变式:如图,如果弧AB=弧CD,
求证:AD=CB
4、如图,已知AB、CD是⊙O中互相垂直的两条直径,又两条弦AE、CF垂直相交与点G,试证明:AE=CF
P
. O
A
B
C
D
┌
┐
G
E
F
如图7所示,CD为⊙O的弦,在CD上取CE=DF,连结OE、OF,并延长交⊙O于点A、B。
(1)试判断△OEF的形状,并说明理由;
(2)求证:弧AC=弧BD
拓展训练
例题解析
例2 已知:如图2,AB、CD是⊙O的弦,且AB与CD不平行,M、N分别是AB、CD的中点,AB=CD,那么∠AMN与∠CNM的大小关系是什么?为什么?
解:连结OM、ON,
∵M、N分别为弦AB、CD的中点,
∴∠AMO=∠CNO=90°
∵ AB=CD
∴ OM=ON
∴∠OMN=∠CNM
∴∠AMN=∠CNM
D
O
B
A
C
M
N
3、如图,点O是∠EPF角平分线上的一点,以O为圆心的圆和角的两边分别交于点A、B和C、D。
求证:AB= CD。
O
A
B
P
C
D
E
F
M
N
基础练习
如图,⊙O中两条相等的弦AB、CD分别延长到E、F,使BE= DF。
求证:EF的垂直平分线必经过点O。
O
A
B
C
D
E
F
M
N
课后思考题
A
B
O
M
N
P
如图,MN为圆O的直径,已知点A是半圆上个三等分点,点B是弧AN的中点,点P是半径ON上的动点,若圆O的半径为1,求AP+BP的最小值.
如图已知弧AD所对的圆心角为90度,点B,C将弧AD三等分,弦AD与半径0B,OC相交于点E,F,
求证:AE=BC=FD
D
C
A
B
O
八、作业
1、教材87-88页
2,3, 10,12
同课章节目录
