四川省绵阳市第一高级中学2021-2022学年高一上学期期中教学质量测试数学试卷(PDF版含答案解析)
文档属性
| 名称 | 四川省绵阳市第一高级中学2021-2022学年高一上学期期中教学质量测试数学试卷(PDF版含答案解析) |  | |
| 格式 | |||
| 文件大小 | 400.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-20 21:44:29 | ||
图片预览



文档简介
秘密 * 启用前 【考试时间:2021 年 11 月 4 日 14:30-16:30】
高中 2021 级第 1 学期期中教学质量测试
数学试题
(时间:120分钟 满分:150分)
温馨提示:
1、请用 0.5毫米黑色签字笔将班级、考号、姓名填写在答卷相应栏目内(非网阅模式还应在机读卡
上填写),再用 2B铅笔在答卷(或机读卡)上填涂考号和科目。
2、选择题答案用 2B铅笔填涂在答卷(或机读卡)上,非选择题用 0.5毫米黑色签字笔书写在答卷
对应栏目内。
第Ⅰ卷(选择题,共 60分)
一.选择题(共 12个小题,每个小题 5分,共 60分。每小题只.有.一.个.选项符合题意)
1.下列描述正确的有( )
(1 2 2)很小的实数可以构成集合; (2)集合 y y x 与 x, y y x 集合是同一个集合;
(3)1,
3 , 6 , 1 ,0.5这些数组成的集合有 5个元素; (4)偶数集可以表示为 x x 2k ,k Z .
2 4 2
A.3个 B.2个 C.1个 D.0个
2.计算 lg 4 lg 25 ( )
A. 2 B.3 C. 4 D.10
3.已知函数 y f (x)的对应关系如下表,函数 y g(x)的图象是如图的曲线 ABC,其中 A(1,3),
B(2,1),C(3, 2),则 f (g(2))的值为( )
A.3 B.2 C.1 D.0
4.已知集合 A={1,3, m},B={1,m},A∪B=A,则 m等于( )
A.0或 3 B.0或 3
C.1或 3 D.1或 3
5.下列是从集合 A到集合 B的函数的是( )
A. A=B=N﹡,对应法则 f : x y x 3
1
1, (x 0)
B. A=R,B={0,1},对应法则 f : x y
0, (x 0)
C. A=B=R,对应法则 f : x y x
1
D. A=Z,B=Q,对应法则 f : x y
x
6.以下四组数中大小比较正确的是 ( )
A. 0.2 -0.1 B. 0.50.3 0.40.3 C. log3.1 log 3.1 D. 0.40.3 0.10.7
7.函数 f x 2x 1 ln 1 x 的定义域是( )
4
A. 1,2 B. 2,1 C. 2,1 D. 2,1
1
8.若 f(x)满足关系式 f(x)+2f( )=3x,则 f(2)的值为( )
x
3 3
A.﹣1 B.1 C. D.
2 2
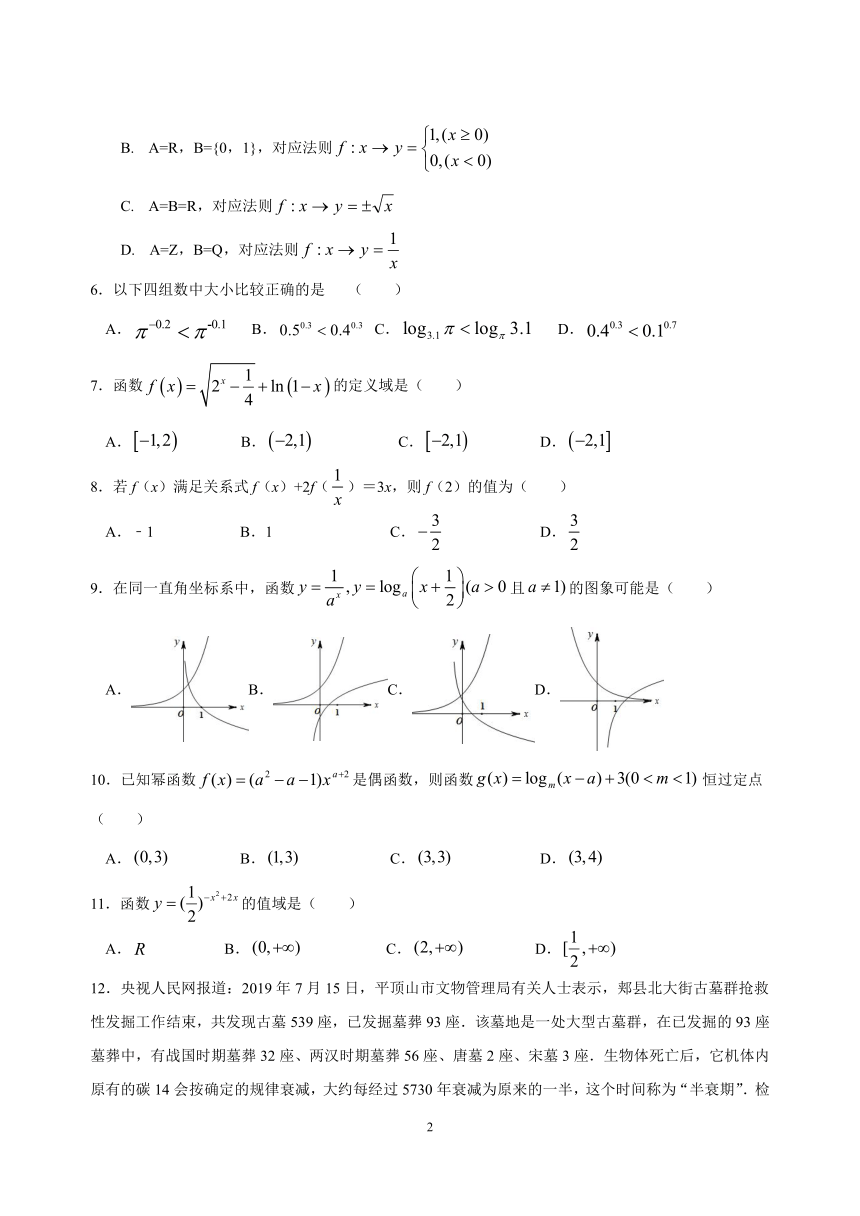
y 19.在同一直角坐标系中,函数 x , y
1
log a x (a 0且 a 1)的图象可能是( )a 2
A. B. C. D.
10.已知幂函数 f (x) (a2 a 1)x a 2 是偶函数,则函数 g(x) logm(x a) 3(0 m 1) 恒过定点
( )
A. (0,3) B. (1,3) C. (3,3) D. (3,4)
1 2
11.函数 y ( ) x 2x的值域是( )
2
A. R B. (0, ) C. (2, ) [
1
D. , )
2
12.央视人民网报道:2019年 7月 15日,平顶山市文物管理局有关人士表示,郏县北大街古墓群抢救
性发掘工作结束,共发现古墓 539座,已发掘墓葬 93座.该墓地是一处大型古墓群,在已发掘的 93座
墓葬中,有战国时期墓葬 32座、两汉时期墓葬 56座、唐墓 2座、宋墓 3座.生物体死亡后,它机体内
原有的碳 14会按确定的规律衰减,大约每经过 5730年衰减为原来的一半,这个时间称为“半衰期”.检
2
测一墓葬女尸出土时碳 14的残余量约占原始含量的 79%,则可推断为该墓葬属于( )时期(辅助
数据: log2 0.79 0.34)
参考时间轴:
A.战国 B.唐朝 C.宋朝 D.两汉
第Ⅱ卷(非选择题,共 90分)
二.填空题(本大题共 4个小题,每小题 5分,共 20分)
13.若 log2 log 1 log2 x 0,则 x ________.
2
14 x.若函数 y a 1(a 0,a 1)与直线 y 2a的图象有两个公共点,
则a的取值范围是 。
15.函数 f x log 22 x 3x 4 的单调减区间为__________.
16.给出下列四个结论
①所以的幂函数都经过定点(0,0)与(1,1);
②已知函数 y loga 2 ax (a 0且 a 1)在 0,1 上是减函数,则 a的取值范围是 1,2 ;
③在同一坐标系中,函数 y log x与 y log2 1 x的图象关于 x轴对称;
2
④在同一坐标系中,函数 y 2x 与 y log2x的图象关于直线 y x对称.
其中正.确.结.论.的序号是__________.
三.解答题(本大题共 6个小题,共 70分)
1
2
2 1 1
a 3 b 1 a 2 b3 1 317(10 log分) (1) (2) log 25 lg ln e 2 2 ; 5a>0,b>0 100
6 a b5
3
18(12分) 已知集合 A x 3 x 7 ,B x 2 x 10 ,C x a x a 1 .
(Ⅰ)求 A∪ B; (Ⅱ)求 (CRA)∩ B; (Ⅲ)若C A,求 a的取值范围.
19 (12分)已知 a 0且满足不等式 22a 1 25a 2 .
(1) 求不等式 loga 3x 1 loga 7 5x ;
(2)若函数 y loga 2x 1 在区间 3,6 有最小值为 2,求实数 a值.
x
20 a 1(12分)已知函数 f (x) (a>1).
a x 1
(1)判断函数 f (x)的奇偶性;
(2)求 f (x)的值域;
(3)证明 f (x)在(-∞,+∞)上是增函数.
21(12分) 某商品在近 30天内每件的销售价格 P元和时间 t(t∈N)的关系如图所示.
(1)请确定销售价格 P(元)和时间 t(天)的函数解析式;
(2)该商品的日销售量 Q(件)与时间 t(天)的关系是:Q=﹣t+40(0≤t≤30,t∈N),求该商品
的日销售金额 y(元)与时间 t(天)的函数解析式;
(3)求该商品的日销售金额 y(元)的最大值,并指出日销售金额最大的一天是 30天中的哪一天?
22(12分) 已知二次函数 f x 满足 f (0) 2,且 f (x 1) f (x) 2x 3 .
(1)求 f x 的解析式;
(2)设函数 h(x) f (x) 2tx,当 x [1, )时,求 h x 的最小值;
(3)设函数 g x log 1 x+m若对任意 x1 [1, 4],总存在 x2 [1, 4],使得 f x1 g x2 成立,
2
求 m的取值范围.
4
数学试题答案
1【答案】C 2.【答案】A 3【答案】B
4【答案】B 5【答案】B
6【答案】A 解:对 A, y x为增函数,故 0.2 -0.1,正确;对 B, y x0.3在第一象限为增函
数,故 0.50.3 0.40.3 ,错误;对 C,log3.1 1, log 3.1 1,故 log 0.33.1 log 3.1,错误;对 D,0.4 0.10.3,
0.10.3 0.10.7 ,故 0.40.3 0.10.7,错误; 故选:A
2x 1 0
7【答案】C 解:由题意得,{ 4 2 x 1,故函数 f (x)的定义域为 2,1 ,故选 C.1 x 0
1
1
f (2) 2 f 6,①
2
8【答案】A 解:∵f(x)满足关系式 f(x)+2f( )=3x, ∴
x f 1 3 2 f (2) ,②
2 2
①﹣②×2得﹣3f(2)=3, ∴f(2)=﹣1, 故选:A
1
9.【答案】C 解:当0 a 1时,函数 y a x过定点 (0,1)且单调递减,则函数 y 过定点 (0,1)且
ax
y log x 1 1单调递增,函数 a 过定点 ( ,0)且单调递减,C选项符合;当 a 1时,函数 y a x过定
2 2
点 (0,1) 1
1 1
且单调递增,则函数 y 过定点 (0,1)x 且单调递减,函数 y loga x 过定点 ( ,0)且单a 2 2
调递增,各选项均不符合.
10【答案】C 解:因为 f (x) (a2 a 1)x a 2 是幂函数,所以 a2 a 1 1得 a 2或 a 1,
又 f (x) (a2 a 1)x a 2 是偶函数,所以 a 2,函数 g(x) logm (x 2) 3(0 m 1)恒过定点 (3,3)
1 t 1 t 1
11【答案】D 解:令 t x2 2x,则 y ( ) ,而 t x2 2x (x 1)2 1 1,所以 y ( ) .
2 2 2
t
P t 1 573012【答案】D 解:生物体内碳 14 的含量 与死亡年数 之间的函数关系式为P (t 0)
2
t
1 5730P 0.79
t log 0.79 t 5730 log 1 0.79 5730 log2 0.79 1948
2 5730 1 22
2019 1948 71,对应朝代为汉
1
13【答案】 2 解 log 1 log2 x 1 log2 x
1
2,故 x 2 .故答案为: 22
0 114【答案】( ,)
2
15【答案】 ( , 1) 解:函数 f (x) log x22 3x 4 ,
则 x2 3x 4 0 x 4 x 1 0 x 4或 x 1,故函数 f x 的定义域为 x 4或 x 1,
由 y log2 x是单调递增函数,可知函数 f x 的单调减区间即 y x2 3x 4的单调减区间,
x 3当 ,
时,函数 y x2 3x 4单调递减,结合 f x 的定义域,
2
2
可得函数 f (x) log2 x 3x 4 的单调减区间为 ( , 1).
16【答案】③ ④ 对于①,终边在 y轴上的角的集合是 , ①错误;
a 1
对于②,函数 y loga 2 ax (a 0且 a 1)在 0,1 上是减函数, 2 a 0,解得 a 的取值范围
是 1,2 ,②错误;对于③,在同一坐标系中,函数 y log2x与 y log 1 x的图象关于 x轴对称,③
2
正确;对于④,在同一坐标系中,函数 y 2x 与 y log2x的图象关于直线 y x对称,④正确.
7
17【答案】(1)1 (2)
2
1
2
2 1 1
1
a 3 b a 2 b3 1 1 1 1
解:(1) a 3 b 2 a 2 b3 1 1 1 1 1 5 a 3 2 6 b 2 3 6 1
6 5 1 5a b a 6 b6
1
3 3
log5 25 lg
1
ln e 2log2 log 52 lg10 2 ln e2 2log2 2 2 1 7 3
(2) 100
5 2 2
18【答案】(Ⅰ) x 2 x 10 ;(Ⅱ) (CRA) B {2 x 3或7 x 10};(Ⅲ)3 a 6
【详解】 (Ⅰ) A B {x | 2 x 10};
(Ⅱ)CRA {x | x 3或 x 7},∴ (CRA) B {2 x 3或7 x 10};
2
a 3
C A a 1 7(Ⅲ)∵ ,∴ ,解得3 a 6
3 , 7 1119【答案】(1) ;(2) .
4 5 11
解:(1)∵22a+1>25a-2. ∴2a+1>5a-2,即 3a<3∴a<1, ∵a>0,a<1 ∴0<a<1.
∵loga(3x+1)<loga(7-5x).
1
x>
3x 1>0 3
7 3 7 3 7
∴等价为 7 5x>0 , 即 x< , ∴ <x< , 即不等式的解集为( , ).
5 4 5 4 5
3x 1>7 5x 3
x> 4
(2)∵0<a<1∴函数 y=loga(2x-1)在区间[3,6]上为减函数,
1
∴当 x=6时,y有最小值为-2, 即 log 11=-2 a-2= =11 a= 11a , ∴ 2 , 解得 .a 11
20【答案】(1)是奇函数.(2)值域为(-1,1).(3)见解析.
a x 1 1 a x
解:(1)f(x) 定义域为 R f x f x 所以函数是奇函数.
a x 1 1 a x
a x 1 a x 2
(2) f x 1 2 2 1 ,令 t a x ,t 0,则 y 1 , t 0
a x 1 a x 1 ax 1 t 1
2
由反比例函数性质可知:函数 y 1 , t 0单调递增,所以 f(x)的值域为(-1,1).
t 1
a x1 1 a x2 1 a x1 1 a x2 1 a x1 1 a x2 1
(3)设 x1 x2,则 f x1 f x2 =a x 1 1 a x2 1 a x1 1 a x2 1
∵ a 1, x x1 x2 x11 x2 ,∴a a . 又∵ a 1 0,a x2 1 0
∴ f (x1) f (x2 ) 0, 即 f (x1) f (x2 ),函数 f(x)在(-∞,+∞)上是增函数.
t 19,0 t 25, t N
21【答案】(1) P ;
t 100,25 t 30, t N
t 2 21t 760, 0 t 25, t N (3)第 25 天,日销售金额有最大值 1125 元. 3 由y
t
2 140t 4000, 25 t 30, t N
3
19 b a 1
解:(1)当 0≤t<25,t∈N,设 P=at+b,将(0,19),(25,44)代入得 ,解之得 ,
44 25a b b 19
∴P=t+19(0≤t<25,t∈N),当 25≤t≤30,t∈N,同理可得 P=﹣t+100,
t 19,0 t 25, t N
综上所述:销售价格 P(元)和时间 t(天)的函数解析式为 P .
t 100,25 t 30, t N
t 19 t 40 ,0 t 25, t N
(2)由题意得,y=P Q,由(1)得 y , t 100 t 40 ,25 t 100, t N
t 2 21t 760, 0 t 25, t N
即y
t 2 140t 4000, 25 t 30, t N
2
3 t 21t 760, 0 t 25, t N 由y
t
2 140t 4000, 25 t 30, t N
当 0≤t<25,t∈N,由二次函数的图象和性质知 t=10,或 t=11时,y取最大值 870元
当 25≤t≤30,t∈N,由二次函数的图象和性质知 t=25时,y取最大值 1125元
综上所述,在第 25天,日销售金额有最大值 1125元
5 2t, t 2,
22【答案】(1) f (x) x2 2x 2;(2) h(x)min 2 ;(3)m 7
t 2t 1,t 2.
解:(1)设 f (x) ax2 bx c(a 0) .①∵ f (0) 2,∴ f (0) c 2 ,又∵ f (x 1) f (x) x 1,
∴a(x 1)2 b(x 1) 2 ax2 bx 2 2x 3,可得 2ax a b 2x 3,
2a 1, a 1,
∴ 解得 即 f (x) x2 2x 2 .
a b 3, b 2,
(2)由题意知, h(x) x2 2(1 t)x 2 , x [1, ) ,对称轴为 x t 1.
①当 t 1 1,即 t 2时,函数 h(x)在[1, )上单调递增, 即 h(x)min h(1) 5 2t;
②当 t 1 1,即 t 2时,函数 h(x)在[1, t 1)上单调递减,在[t 1, )上单调递增,
5 2t, t 2,
即 h(x)min h(t 1) t
2 2t 1. 综上, h(x)min t 2 2t 1,t 2.
(3)由题意可知 f (x)min g(x)min ,∵函数 f x 在[1, 4]上单调递增,故最小值为 f (x)min f (1) 5 ,
函数 g x 在[1, 4]上单调递减,故最小值为 g(x)min g(4) 2 m ,∴5 2 m ,解得m 7 .
4
高中 2021 级第 1 学期期中教学质量测试
数学试题
(时间:120分钟 满分:150分)
温馨提示:
1、请用 0.5毫米黑色签字笔将班级、考号、姓名填写在答卷相应栏目内(非网阅模式还应在机读卡
上填写),再用 2B铅笔在答卷(或机读卡)上填涂考号和科目。
2、选择题答案用 2B铅笔填涂在答卷(或机读卡)上,非选择题用 0.5毫米黑色签字笔书写在答卷
对应栏目内。
第Ⅰ卷(选择题,共 60分)
一.选择题(共 12个小题,每个小题 5分,共 60分。每小题只.有.一.个.选项符合题意)
1.下列描述正确的有( )
(1 2 2)很小的实数可以构成集合; (2)集合 y y x 与 x, y y x 集合是同一个集合;
(3)1,
3 , 6 , 1 ,0.5这些数组成的集合有 5个元素; (4)偶数集可以表示为 x x 2k ,k Z .
2 4 2
A.3个 B.2个 C.1个 D.0个
2.计算 lg 4 lg 25 ( )
A. 2 B.3 C. 4 D.10
3.已知函数 y f (x)的对应关系如下表,函数 y g(x)的图象是如图的曲线 ABC,其中 A(1,3),
B(2,1),C(3, 2),则 f (g(2))的值为( )
A.3 B.2 C.1 D.0
4.已知集合 A={1,3, m},B={1,m},A∪B=A,则 m等于( )
A.0或 3 B.0或 3
C.1或 3 D.1或 3
5.下列是从集合 A到集合 B的函数的是( )
A. A=B=N﹡,对应法则 f : x y x 3
1
1, (x 0)
B. A=R,B={0,1},对应法则 f : x y
0, (x 0)
C. A=B=R,对应法则 f : x y x
1
D. A=Z,B=Q,对应法则 f : x y
x
6.以下四组数中大小比较正确的是 ( )
A. 0.2 -0.1 B. 0.50.3 0.40.3 C. log3.1 log 3.1 D. 0.40.3 0.10.7
7.函数 f x 2x 1 ln 1 x 的定义域是( )
4
A. 1,2 B. 2,1 C. 2,1 D. 2,1
1
8.若 f(x)满足关系式 f(x)+2f( )=3x,则 f(2)的值为( )
x
3 3
A.﹣1 B.1 C. D.
2 2
y 19.在同一直角坐标系中,函数 x , y
1
log a x (a 0且 a 1)的图象可能是( )a 2
A. B. C. D.
10.已知幂函数 f (x) (a2 a 1)x a 2 是偶函数,则函数 g(x) logm(x a) 3(0 m 1) 恒过定点
( )
A. (0,3) B. (1,3) C. (3,3) D. (3,4)
1 2
11.函数 y ( ) x 2x的值域是( )
2
A. R B. (0, ) C. (2, ) [
1
D. , )
2
12.央视人民网报道:2019年 7月 15日,平顶山市文物管理局有关人士表示,郏县北大街古墓群抢救
性发掘工作结束,共发现古墓 539座,已发掘墓葬 93座.该墓地是一处大型古墓群,在已发掘的 93座
墓葬中,有战国时期墓葬 32座、两汉时期墓葬 56座、唐墓 2座、宋墓 3座.生物体死亡后,它机体内
原有的碳 14会按确定的规律衰减,大约每经过 5730年衰减为原来的一半,这个时间称为“半衰期”.检
2
测一墓葬女尸出土时碳 14的残余量约占原始含量的 79%,则可推断为该墓葬属于( )时期(辅助
数据: log2 0.79 0.34)
参考时间轴:
A.战国 B.唐朝 C.宋朝 D.两汉
第Ⅱ卷(非选择题,共 90分)
二.填空题(本大题共 4个小题,每小题 5分,共 20分)
13.若 log2 log 1 log2 x 0,则 x ________.
2
14 x.若函数 y a 1(a 0,a 1)与直线 y 2a的图象有两个公共点,
则a的取值范围是 。
15.函数 f x log 22 x 3x 4 的单调减区间为__________.
16.给出下列四个结论
①所以的幂函数都经过定点(0,0)与(1,1);
②已知函数 y loga 2 ax (a 0且 a 1)在 0,1 上是减函数,则 a的取值范围是 1,2 ;
③在同一坐标系中,函数 y log x与 y log2 1 x的图象关于 x轴对称;
2
④在同一坐标系中,函数 y 2x 与 y log2x的图象关于直线 y x对称.
其中正.确.结.论.的序号是__________.
三.解答题(本大题共 6个小题,共 70分)
1
2
2 1 1
a 3 b 1 a 2 b3 1 317(10 log分) (1) (2) log 25 lg ln e 2 2 ; 5a>0,b>0 100
6 a b5
3
18(12分) 已知集合 A x 3 x 7 ,B x 2 x 10 ,C x a x a 1 .
(Ⅰ)求 A∪ B; (Ⅱ)求 (CRA)∩ B; (Ⅲ)若C A,求 a的取值范围.
19 (12分)已知 a 0且满足不等式 22a 1 25a 2 .
(1) 求不等式 loga 3x 1 loga 7 5x ;
(2)若函数 y loga 2x 1 在区间 3,6 有最小值为 2,求实数 a值.
x
20 a 1(12分)已知函数 f (x) (a>1).
a x 1
(1)判断函数 f (x)的奇偶性;
(2)求 f (x)的值域;
(3)证明 f (x)在(-∞,+∞)上是增函数.
21(12分) 某商品在近 30天内每件的销售价格 P元和时间 t(t∈N)的关系如图所示.
(1)请确定销售价格 P(元)和时间 t(天)的函数解析式;
(2)该商品的日销售量 Q(件)与时间 t(天)的关系是:Q=﹣t+40(0≤t≤30,t∈N),求该商品
的日销售金额 y(元)与时间 t(天)的函数解析式;
(3)求该商品的日销售金额 y(元)的最大值,并指出日销售金额最大的一天是 30天中的哪一天?
22(12分) 已知二次函数 f x 满足 f (0) 2,且 f (x 1) f (x) 2x 3 .
(1)求 f x 的解析式;
(2)设函数 h(x) f (x) 2tx,当 x [1, )时,求 h x 的最小值;
(3)设函数 g x log 1 x+m若对任意 x1 [1, 4],总存在 x2 [1, 4],使得 f x1 g x2 成立,
2
求 m的取值范围.
4
数学试题答案
1【答案】C 2.【答案】A 3【答案】B
4【答案】B 5【答案】B
6【答案】A 解:对 A, y x为增函数,故 0.2 -0.1,正确;对 B, y x0.3在第一象限为增函
数,故 0.50.3 0.40.3 ,错误;对 C,log3.1 1, log 3.1 1,故 log 0.33.1 log 3.1,错误;对 D,0.4 0.10.3,
0.10.3 0.10.7 ,故 0.40.3 0.10.7,错误; 故选:A
2x 1 0
7【答案】C 解:由题意得,{ 4 2 x 1,故函数 f (x)的定义域为 2,1 ,故选 C.1 x 0
1
1
f (2) 2 f 6,①
2
8【答案】A 解:∵f(x)满足关系式 f(x)+2f( )=3x, ∴
x f 1 3 2 f (2) ,②
2 2
①﹣②×2得﹣3f(2)=3, ∴f(2)=﹣1, 故选:A
1
9.【答案】C 解:当0 a 1时,函数 y a x过定点 (0,1)且单调递减,则函数 y 过定点 (0,1)且
ax
y log x 1 1单调递增,函数 a 过定点 ( ,0)且单调递减,C选项符合;当 a 1时,函数 y a x过定
2 2
点 (0,1) 1
1 1
且单调递增,则函数 y 过定点 (0,1)x 且单调递减,函数 y loga x 过定点 ( ,0)且单a 2 2
调递增,各选项均不符合.
10【答案】C 解:因为 f (x) (a2 a 1)x a 2 是幂函数,所以 a2 a 1 1得 a 2或 a 1,
又 f (x) (a2 a 1)x a 2 是偶函数,所以 a 2,函数 g(x) logm (x 2) 3(0 m 1)恒过定点 (3,3)
1 t 1 t 1
11【答案】D 解:令 t x2 2x,则 y ( ) ,而 t x2 2x (x 1)2 1 1,所以 y ( ) .
2 2 2
t
P t 1 573012【答案】D 解:生物体内碳 14 的含量 与死亡年数 之间的函数关系式为P (t 0)
2
t
1 5730P 0.79
t log 0.79 t 5730 log 1 0.79 5730 log2 0.79 1948
2 5730 1 22
2019 1948 71,对应朝代为汉
1
13【答案】 2 解 log 1 log2 x 1 log2 x
1
2,故 x 2 .故答案为: 22
0 114【答案】( ,)
2
15【答案】 ( , 1) 解:函数 f (x) log x22 3x 4 ,
则 x2 3x 4 0 x 4 x 1 0 x 4或 x 1,故函数 f x 的定义域为 x 4或 x 1,
由 y log2 x是单调递增函数,可知函数 f x 的单调减区间即 y x2 3x 4的单调减区间,
x 3当 ,
时,函数 y x2 3x 4单调递减,结合 f x 的定义域,
2
2
可得函数 f (x) log2 x 3x 4 的单调减区间为 ( , 1).
16【答案】③ ④ 对于①,终边在 y轴上的角的集合是 , ①错误;
a 1
对于②,函数 y loga 2 ax (a 0且 a 1)在 0,1 上是减函数, 2 a 0,解得 a 的取值范围
是 1,2 ,②错误;对于③,在同一坐标系中,函数 y log2x与 y log 1 x的图象关于 x轴对称,③
2
正确;对于④,在同一坐标系中,函数 y 2x 与 y log2x的图象关于直线 y x对称,④正确.
7
17【答案】(1)1 (2)
2
1
2
2 1 1
1
a 3 b a 2 b3 1 1 1 1
解:(1) a 3 b 2 a 2 b3 1 1 1 1 1 5 a 3 2 6 b 2 3 6 1
6 5 1 5a b a 6 b6
1
3 3
log5 25 lg
1
ln e 2log2 log 52 lg10 2 ln e2 2log2 2 2 1 7 3
(2) 100
5 2 2
18【答案】(Ⅰ) x 2 x 10 ;(Ⅱ) (CRA) B {2 x 3或7 x 10};(Ⅲ)3 a 6
【详解】 (Ⅰ) A B {x | 2 x 10};
(Ⅱ)CRA {x | x 3或 x 7},∴ (CRA) B {2 x 3或7 x 10};
2
a 3
C A a 1 7(Ⅲ)∵ ,∴ ,解得3 a 6
3 , 7 1119【答案】(1) ;(2) .
4 5 11
解:(1)∵22a+1>25a-2. ∴2a+1>5a-2,即 3a<3∴a<1, ∵a>0,a<1 ∴0<a<1.
∵loga(3x+1)<loga(7-5x).
1
x>
3x 1>0 3
7 3 7 3 7
∴等价为 7 5x>0 , 即 x< , ∴ <x< , 即不等式的解集为( , ).
5 4 5 4 5
3x 1>7 5x 3
x> 4
(2)∵0<a<1∴函数 y=loga(2x-1)在区间[3,6]上为减函数,
1
∴当 x=6时,y有最小值为-2, 即 log 11=-2 a-2= =11 a= 11a , ∴ 2 , 解得 .a 11
20【答案】(1)是奇函数.(2)值域为(-1,1).(3)见解析.
a x 1 1 a x
解:(1)f(x) 定义域为 R f x f x 所以函数是奇函数.
a x 1 1 a x
a x 1 a x 2
(2) f x 1 2 2 1 ,令 t a x ,t 0,则 y 1 , t 0
a x 1 a x 1 ax 1 t 1
2
由反比例函数性质可知:函数 y 1 , t 0单调递增,所以 f(x)的值域为(-1,1).
t 1
a x1 1 a x2 1 a x1 1 a x2 1 a x1 1 a x2 1
(3)设 x1 x2,则 f x1 f x2 =a x 1 1 a x2 1 a x1 1 a x2 1
∵ a 1, x x1 x2 x11 x2 ,∴a a . 又∵ a 1 0,a x2 1 0
∴ f (x1) f (x2 ) 0, 即 f (x1) f (x2 ),函数 f(x)在(-∞,+∞)上是增函数.
t 19,0 t 25, t N
21【答案】(1) P ;
t 100,25 t 30, t N
t 2 21t 760, 0 t 25, t N (3)第 25 天,日销售金额有最大值 1125 元. 3 由y
t
2 140t 4000, 25 t 30, t N
3
19 b a 1
解:(1)当 0≤t<25,t∈N,设 P=at+b,将(0,19),(25,44)代入得 ,解之得 ,
44 25a b b 19
∴P=t+19(0≤t<25,t∈N),当 25≤t≤30,t∈N,同理可得 P=﹣t+100,
t 19,0 t 25, t N
综上所述:销售价格 P(元)和时间 t(天)的函数解析式为 P .
t 100,25 t 30, t N
t 19 t 40 ,0 t 25, t N
(2)由题意得,y=P Q,由(1)得 y , t 100 t 40 ,25 t 100, t N
t 2 21t 760, 0 t 25, t N
即y
t 2 140t 4000, 25 t 30, t N
2
3 t 21t 760, 0 t 25, t N 由y
t
2 140t 4000, 25 t 30, t N
当 0≤t<25,t∈N,由二次函数的图象和性质知 t=10,或 t=11时,y取最大值 870元
当 25≤t≤30,t∈N,由二次函数的图象和性质知 t=25时,y取最大值 1125元
综上所述,在第 25天,日销售金额有最大值 1125元
5 2t, t 2,
22【答案】(1) f (x) x2 2x 2;(2) h(x)min 2 ;(3)m 7
t 2t 1,t 2.
解:(1)设 f (x) ax2 bx c(a 0) .①∵ f (0) 2,∴ f (0) c 2 ,又∵ f (x 1) f (x) x 1,
∴a(x 1)2 b(x 1) 2 ax2 bx 2 2x 3,可得 2ax a b 2x 3,
2a 1, a 1,
∴ 解得 即 f (x) x2 2x 2 .
a b 3, b 2,
(2)由题意知, h(x) x2 2(1 t)x 2 , x [1, ) ,对称轴为 x t 1.
①当 t 1 1,即 t 2时,函数 h(x)在[1, )上单调递增, 即 h(x)min h(1) 5 2t;
②当 t 1 1,即 t 2时,函数 h(x)在[1, t 1)上单调递减,在[t 1, )上单调递增,
5 2t, t 2,
即 h(x)min h(t 1) t
2 2t 1. 综上, h(x)min t 2 2t 1,t 2.
(3)由题意可知 f (x)min g(x)min ,∵函数 f x 在[1, 4]上单调递增,故最小值为 f (x)min f (1) 5 ,
函数 g x 在[1, 4]上单调递减,故最小值为 g(x)min g(4) 2 m ,∴5 2 m ,解得m 7 .
4
同课章节目录
