第二章 第1课时 勾股定理(1) 课时训练(含答案)
文档属性
| 名称 | 第二章 第1课时 勾股定理(1) 课时训练(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 34.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-30 00:00:00 | ||
图片预览

文档简介
第二章 勾股定理与平方根
第1课时 勾股定理(1)
【基础巩固】
1.已知一直角三角形两直角边的长分别是3,4,则斜边的长是_______.
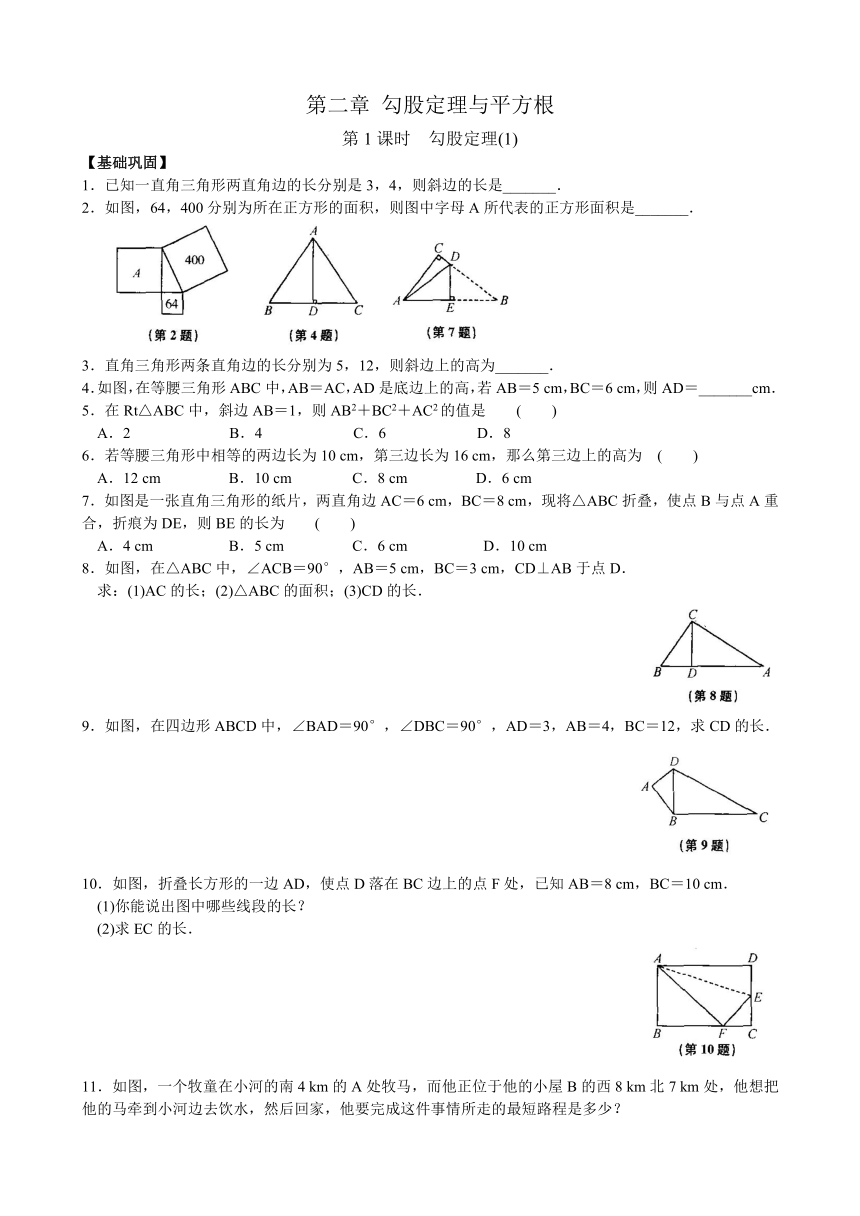
2.如图,64,400分别为所在正方形的面积,则图中字母A所代表的正方形面积是_______.
3.直角三角形两条直角边的长分别为5,12,则斜边上的高为_______.
4.如图,在等腰三角形ABC中,AB=AC,AD是底边上的高,若AB=5 cm,BC=6 cm,则AD=_______cm.
5.在Rt△ABC中,斜边AB=1,则AB2+BC2+AC2的值是 ( )
A.2 B.4 C.6 D.8
6.若等腰三角形中相等的两边长为10 cm,第三边长为16 cm,那么第三边上的高为 ( )
A.12 cm B.10 cm C.8 cm D.6 cm
7.如图是一张直角三角形的纸片,两直角边AC=6 cm,BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为 ( )
A.4 cm B.5 cm C.6 cm D.10 cm
8.如图,在△ABC中,∠ACB=90°,AB=5 cm,BC=3 cm,CD⊥AB于点D.
求:(1)AC的长;(2)△ABC的面积;(3)CD的长.
9.如图,在四边形ABCD中,∠BAD=90°,∠DBC=90°,AD=3,AB=4,BC=12,求CD的长.
10.如图,折叠长方形的一边AD,使点D落在BC边上的点F处,已知AB=8 cm,BC=10 cm.
(1)你能说出图中哪些线段的长?
(2)求EC的长.
11.如图,一个牧童在小河的南4 km的A处牧马,而他正位于他的小屋B的西8 km北7 km处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?
【拓展提优】
12.一个直角三角形三边的长为连续自然数,则这三个数分别为_______.
13.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形A、B、C、D的面积的和是_______.
14.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了_______步路(假设2步为1 m),却踩伤了花草.
15.如图,利用图①或图②两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为_______,该定理的结论其数学表达式是_______.
16.已知一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度从港口A出发向东南方向航行,离开港口1小时后,两船相距 ( )
A.10海里
B.15海里
C.20海里
D.25海里
17.如图,有一个直角三角形纸片,两直角边AC=6 cm,BC=8 cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
18.如图是一个三级台阶,它的每一级的长、宽、高分别为20 dm,3 dm,2 dm,A和B是这个台阶两相对的端点,A点有一只昆虫想到B点去吃可口的食物,则昆虫沿着台阶爬到B点的最短路程是多少?
19.若Rt△ABC三边的长分别是x,x+1和5,则△ABC的周长=_______.△ABC的面积=_______.
20.如图,已知在△ABC中,AD⊥BC.AB+CD=AC+BD,求证:AB=AC.
参考答案
【基础巩固】
1.5 2.336 3. 4.4 5.A 6.D 7.B 8.(1)4 (2)6 (3) 9.CD=13 10.(1)AF=AD=BC=10,DC=AB=8,BF=6,CF=4 (2)EC=3 11.17 km
【拓展提优】
12.3,4,5 13.49 cm2 14.4 15.勾股定理 16.C 17.CD=3
18.25 dm
19.12或30 6或30
20.略
第1课时 勾股定理(1)
【基础巩固】
1.已知一直角三角形两直角边的长分别是3,4,则斜边的长是_______.
2.如图,64,400分别为所在正方形的面积,则图中字母A所代表的正方形面积是_______.
3.直角三角形两条直角边的长分别为5,12,则斜边上的高为_______.
4.如图,在等腰三角形ABC中,AB=AC,AD是底边上的高,若AB=5 cm,BC=6 cm,则AD=_______cm.
5.在Rt△ABC中,斜边AB=1,则AB2+BC2+AC2的值是 ( )
A.2 B.4 C.6 D.8
6.若等腰三角形中相等的两边长为10 cm,第三边长为16 cm,那么第三边上的高为 ( )
A.12 cm B.10 cm C.8 cm D.6 cm
7.如图是一张直角三角形的纸片,两直角边AC=6 cm,BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为 ( )
A.4 cm B.5 cm C.6 cm D.10 cm
8.如图,在△ABC中,∠ACB=90°,AB=5 cm,BC=3 cm,CD⊥AB于点D.
求:(1)AC的长;(2)△ABC的面积;(3)CD的长.
9.如图,在四边形ABCD中,∠BAD=90°,∠DBC=90°,AD=3,AB=4,BC=12,求CD的长.
10.如图,折叠长方形的一边AD,使点D落在BC边上的点F处,已知AB=8 cm,BC=10 cm.
(1)你能说出图中哪些线段的长?
(2)求EC的长.
11.如图,一个牧童在小河的南4 km的A处牧马,而他正位于他的小屋B的西8 km北7 km处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?
【拓展提优】
12.一个直角三角形三边的长为连续自然数,则这三个数分别为_______.
13.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形A、B、C、D的面积的和是_______.
14.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了_______步路(假设2步为1 m),却踩伤了花草.
15.如图,利用图①或图②两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为_______,该定理的结论其数学表达式是_______.
16.已知一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度从港口A出发向东南方向航行,离开港口1小时后,两船相距 ( )
A.10海里
B.15海里
C.20海里
D.25海里
17.如图,有一个直角三角形纸片,两直角边AC=6 cm,BC=8 cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
18.如图是一个三级台阶,它的每一级的长、宽、高分别为20 dm,3 dm,2 dm,A和B是这个台阶两相对的端点,A点有一只昆虫想到B点去吃可口的食物,则昆虫沿着台阶爬到B点的最短路程是多少?
19.若Rt△ABC三边的长分别是x,x+1和5,则△ABC的周长=_______.△ABC的面积=_______.
20.如图,已知在△ABC中,AD⊥BC.AB+CD=AC+BD,求证:AB=AC.
参考答案
【基础巩固】
1.5 2.336 3. 4.4 5.A 6.D 7.B 8.(1)4 (2)6 (3) 9.CD=13 10.(1)AF=AD=BC=10,DC=AB=8,BF=6,CF=4 (2)EC=3 11.17 km
【拓展提优】
12.3,4,5 13.49 cm2 14.4 15.勾股定理 16.C 17.CD=3
18.25 dm
19.12或30 6或30
20.略
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
