第二章 第2课时 勾股定理(2) 课时训练(含答案)
文档属性
| 名称 | 第二章 第2课时 勾股定理(2) 课时训练(含答案) | 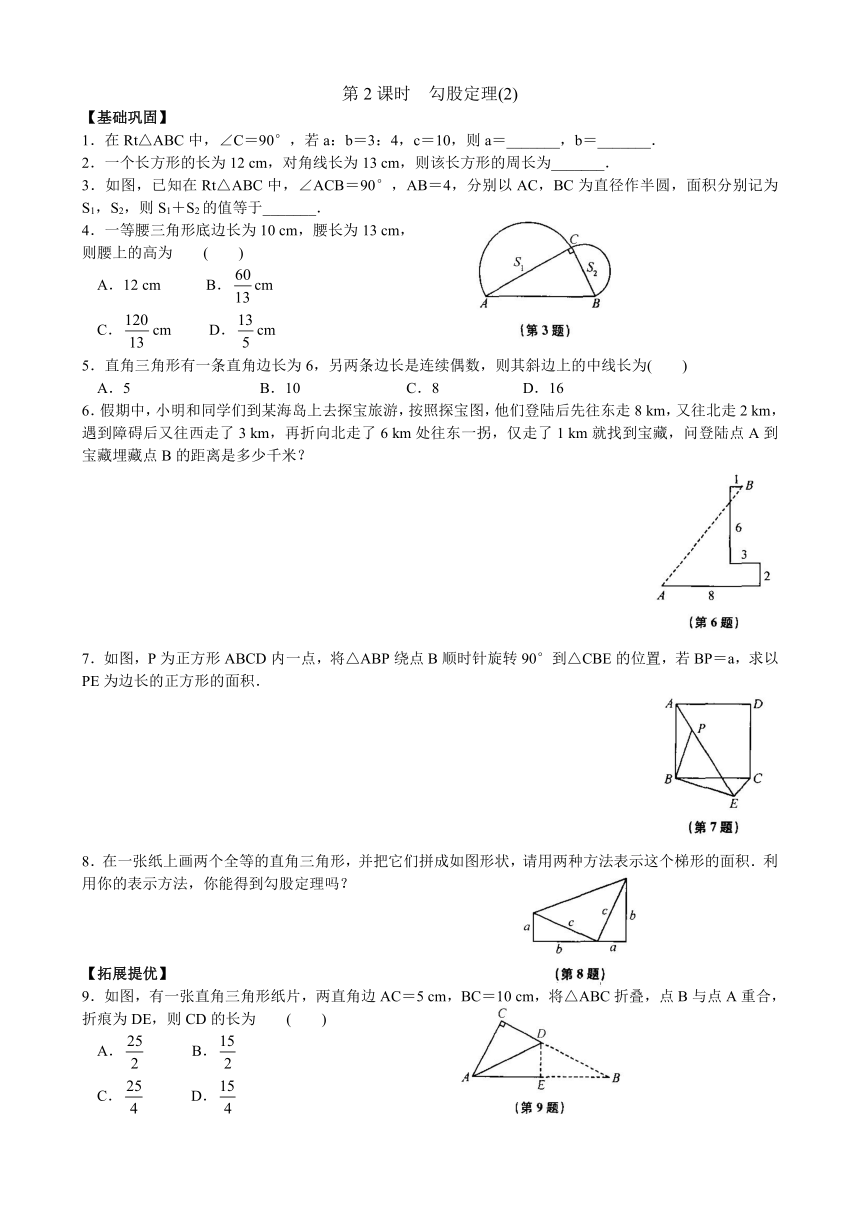 | |
| 格式 | zip | ||
| 文件大小 | 35.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-30 00:07:37 | ||
图片预览

文档简介
第2课时 勾股定理(2)
【基础巩固】
1.在Rt△ABC中,∠C=90°,若a:b=3:4,c=10,则a=_______,b=_______.
2.一个长方形的长为12 cm,对角线长为13 cm,则该长方形的周长为_______.
3.如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于_______.
4.一等腰三角形底边长为10 cm,腰长为13 cm,
则腰上的高为 ( )
A.12 cm B.cm
C.cm D.cm
5.直角三角形有一条直角边长为6,另两条边长是连续偶数,则其斜边上的中线长为( )
A.5 B.10 C.8 D.16
6.假期中,小明和同学们到某海岛上去探宝旅游,按照探宝图,他们登陆后先往东走8 km,又往北走2 km,遇到障碍后又往西走了3 km,再折向北走了6 km处往东一拐,仅走了1 km就找到宝藏,问登陆点A到宝藏埋藏点B的距离是多少千米?
7.如图,P为正方形ABCD内一点,将△ABP绕点B顺时针旋转90°到△CBE的位置,若BP=a,求以PE为边长的正方形的面积.
8.在一张纸上画两个全等的直角三角形,并把它们拼成如图形状,请用两种方法表示这个梯形的面积.利用你的表示方法,你能得到勾股定理吗?
【拓展提优】
9.如图,有一张直角三角形纸片,两直角边AC=5 cm,BC=10 cm,将△ABC折叠,点B与点A重合,折痕为DE,则CD的长为 ( )
A. B.
C. D.
10.已知一个直角三角形的两边长分别为3和4,则第三边长的平方是 ( )
A.25 B.14 C.7 D.7或25
11.有一个长为12 cm,宽为4 cm,高为3 cm的长方体形铁盒,在其内部要放一根笔直的铁丝,则铁丝最长达到_______cm.
12.已知Rt△ABC的周长是24,斜边上的中线长是5,则S△ABC=_______.
13.如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为_______.
14.如图,在四边形ABCD中,已知AB:BC:CD:DA=2:2;3:1,且∠B=90°,则∠DAB=_______.
15.如图是用硬纸板做成的四个全等的直角三角形,两直角边长分别为a,b,斜边长为c和一个边长为c的正方形,请你将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图.
(2)证明勾股定理.
16.如图是一个高18 m,底面周长为5m的圆柱形水塔,现制造一个螺旋形登梯,为了减小坡度,要求登梯绕塔环绕一周半到达顶端,问登梯至少多长?(建议:拿一张白纸动手操作,你一定会发现其中的奥妙)
17.如图是一株美丽的勾股树,其中所有的四边形都是正方形,
所有的三角形都是直角三角形,若正方形A、B、C、D的边长
分别是3,5,2,3,则最大正方形E的面积是 ( )
A.13 B.26 C.47 D.94
18.如图,自△ABC内的任一点P,作三角形三条边的垂线:PD⊥BC,PE⊥CA,PF⊥AB,若BD=BF,CD=CE.
求证:AE=AF.
参考答案
【基础巩固】
1.6 8 2.34 cm 3.2π 4.C 5.A 6.10.km 7.2a2 8.略
【拓展提优】
9.D 10.D 11.13 12.24 13. 14.135° 15.(1)略 (2)略 16.19cm
17.C 18.略
【基础巩固】
1.在Rt△ABC中,∠C=90°,若a:b=3:4,c=10,则a=_______,b=_______.
2.一个长方形的长为12 cm,对角线长为13 cm,则该长方形的周长为_______.
3.如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于_______.
4.一等腰三角形底边长为10 cm,腰长为13 cm,
则腰上的高为 ( )
A.12 cm B.cm
C.cm D.cm
5.直角三角形有一条直角边长为6,另两条边长是连续偶数,则其斜边上的中线长为( )
A.5 B.10 C.8 D.16
6.假期中,小明和同学们到某海岛上去探宝旅游,按照探宝图,他们登陆后先往东走8 km,又往北走2 km,遇到障碍后又往西走了3 km,再折向北走了6 km处往东一拐,仅走了1 km就找到宝藏,问登陆点A到宝藏埋藏点B的距离是多少千米?
7.如图,P为正方形ABCD内一点,将△ABP绕点B顺时针旋转90°到△CBE的位置,若BP=a,求以PE为边长的正方形的面积.
8.在一张纸上画两个全等的直角三角形,并把它们拼成如图形状,请用两种方法表示这个梯形的面积.利用你的表示方法,你能得到勾股定理吗?
【拓展提优】
9.如图,有一张直角三角形纸片,两直角边AC=5 cm,BC=10 cm,将△ABC折叠,点B与点A重合,折痕为DE,则CD的长为 ( )
A. B.
C. D.
10.已知一个直角三角形的两边长分别为3和4,则第三边长的平方是 ( )
A.25 B.14 C.7 D.7或25
11.有一个长为12 cm,宽为4 cm,高为3 cm的长方体形铁盒,在其内部要放一根笔直的铁丝,则铁丝最长达到_______cm.
12.已知Rt△ABC的周长是24,斜边上的中线长是5,则S△ABC=_______.
13.如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为_______.
14.如图,在四边形ABCD中,已知AB:BC:CD:DA=2:2;3:1,且∠B=90°,则∠DAB=_______.
15.如图是用硬纸板做成的四个全等的直角三角形,两直角边长分别为a,b,斜边长为c和一个边长为c的正方形,请你将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图.
(2)证明勾股定理.
16.如图是一个高18 m,底面周长为5m的圆柱形水塔,现制造一个螺旋形登梯,为了减小坡度,要求登梯绕塔环绕一周半到达顶端,问登梯至少多长?(建议:拿一张白纸动手操作,你一定会发现其中的奥妙)
17.如图是一株美丽的勾股树,其中所有的四边形都是正方形,
所有的三角形都是直角三角形,若正方形A、B、C、D的边长
分别是3,5,2,3,则最大正方形E的面积是 ( )
A.13 B.26 C.47 D.94
18.如图,自△ABC内的任一点P,作三角形三条边的垂线:PD⊥BC,PE⊥CA,PF⊥AB,若BD=BF,CD=CE.
求证:AE=AF.
参考答案
【基础巩固】
1.6 8 2.34 cm 3.2π 4.C 5.A 6.10.km 7.2a2 8.略
【拓展提优】
9.D 10.D 11.13 12.24 13. 14.135° 15.(1)略 (2)略 16.19cm
17.C 18.略
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
