北师大版八年级数学上册第一章勾股定理单元检测卷(Word版,含答案解析)
文档属性
| 名称 | 北师大版八年级数学上册第一章勾股定理单元检测卷(Word版,含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 385.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 14:29:58 | ||
图片预览

文档简介
北师大版八年级上册第一章
勾股定理
一、单选题
1.(2019八下·南岸期中)有四个三角形,分别满足下列条件,其中直角三角形有( )
( 1 )一个内角等于另外两个内角之差:(2)三个内角度数之比为3:4:5;(3)三边长度之比为5:12:13;(4)三边长分别为7、24、25.
A. 1个 B. 2个 C. 3个 D. 4个
2.(2019八下·丹江口期末)矩形ABCD中,已知AB=5,AD=12,则AC长为( )
A. 9 B. 13 C. 17 D. 20
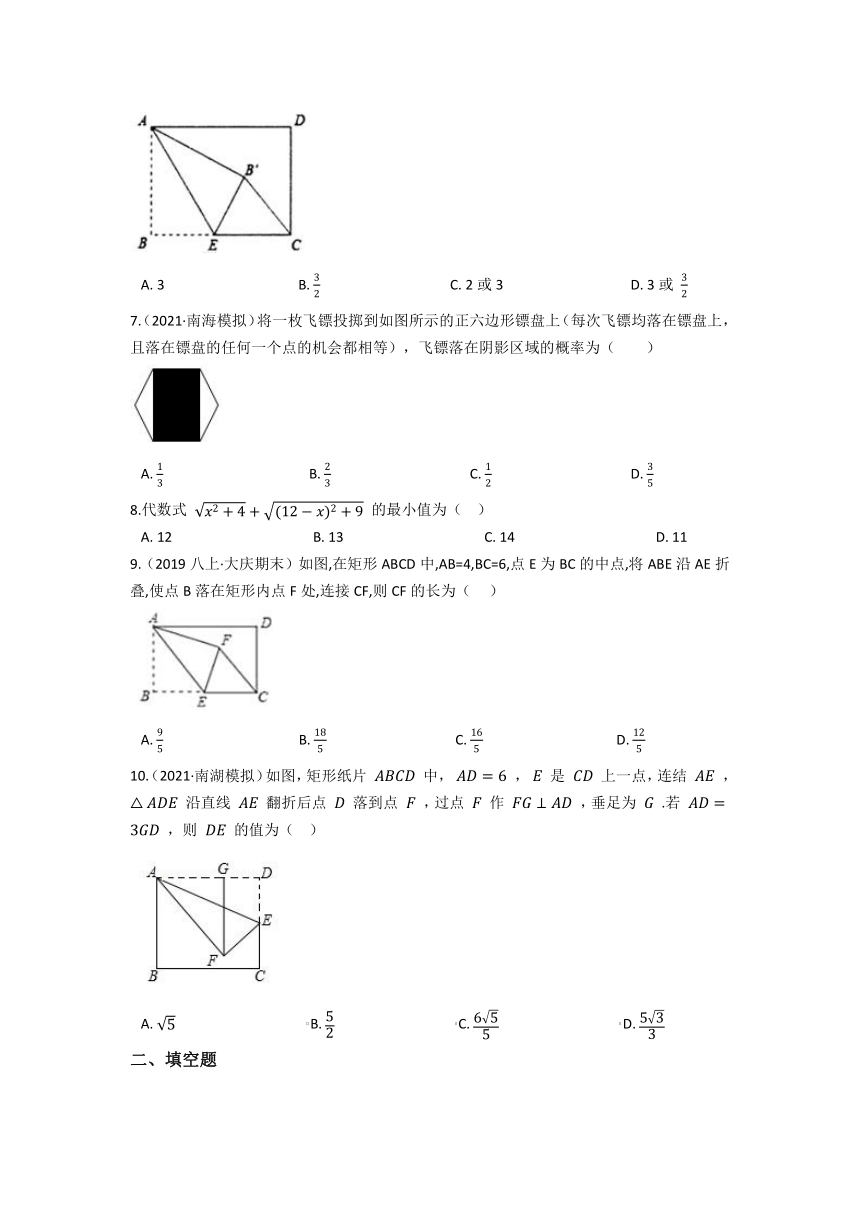
3.(2020八下·江夏月考)如图,网格中每个小正方形的边长均为1,点A,B,C都在格点上,以A为圆心,AB为半径画弧,交最上方的网格线于点D,则图中线段CD的长是( )
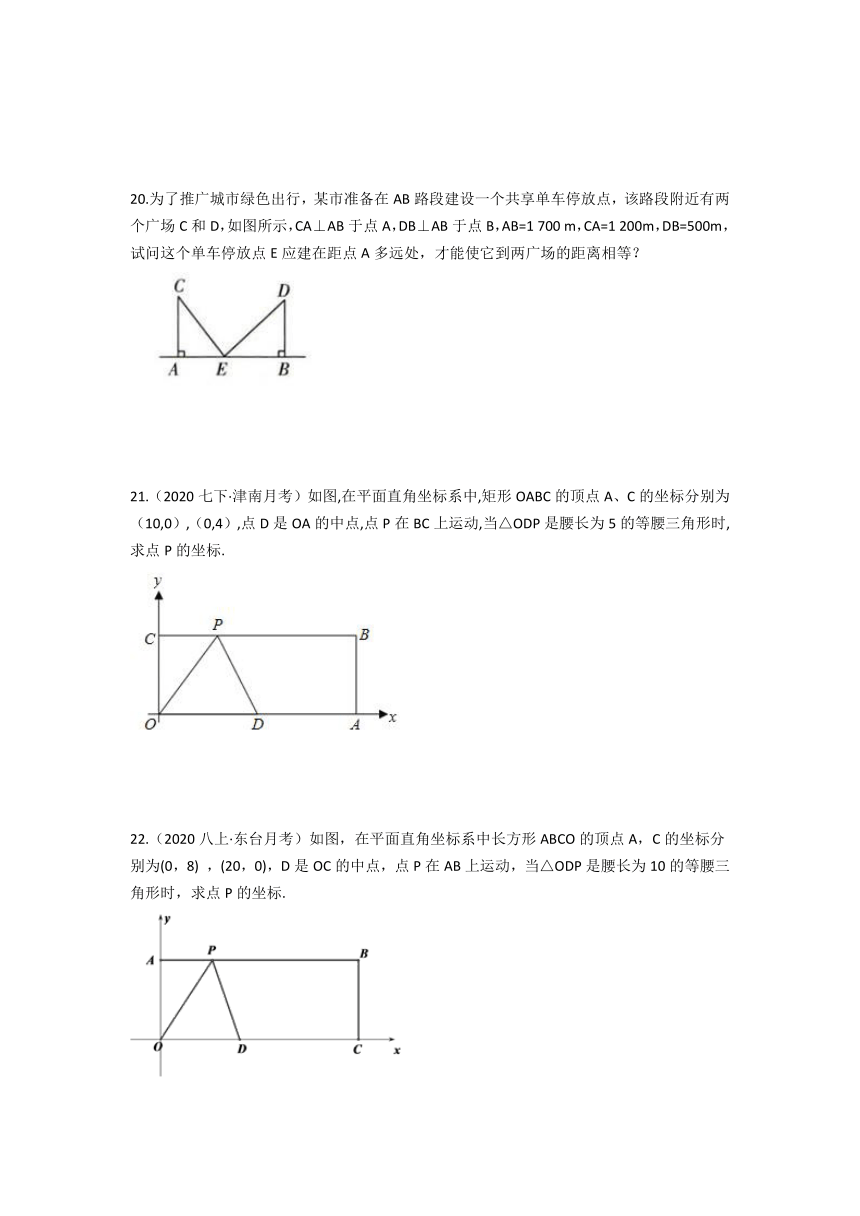
A. 0.8 B. C. D. 3-
4.(2020·昆明模拟)如图,折叠矩形ABCD的一边AD , 使点D落在BC边的点F处,已知折痕AE=5 cm , 且tan∠EFC= ,那么矩形ABCD的周长为( )
A. 18 B. 25 C. 32 D. 36
5.(2020八上·盐城期中)如图,在赵爽弦图中,已知直角三角形的短直角边长为a,长直角边长为b,大正方形的面积为20,小正方形的面积为4,则 的值是( )
A. 10 B. 8 C. 7 D. 5
6.(2019八下·武安期末)如图,矩形 中, , ,点 是 边上一点,连接 ,把 沿 折叠,使点 落在点 处,当 为直角三角形时, 的长为( )
A. 3 B. C. 2或3 D. 3或
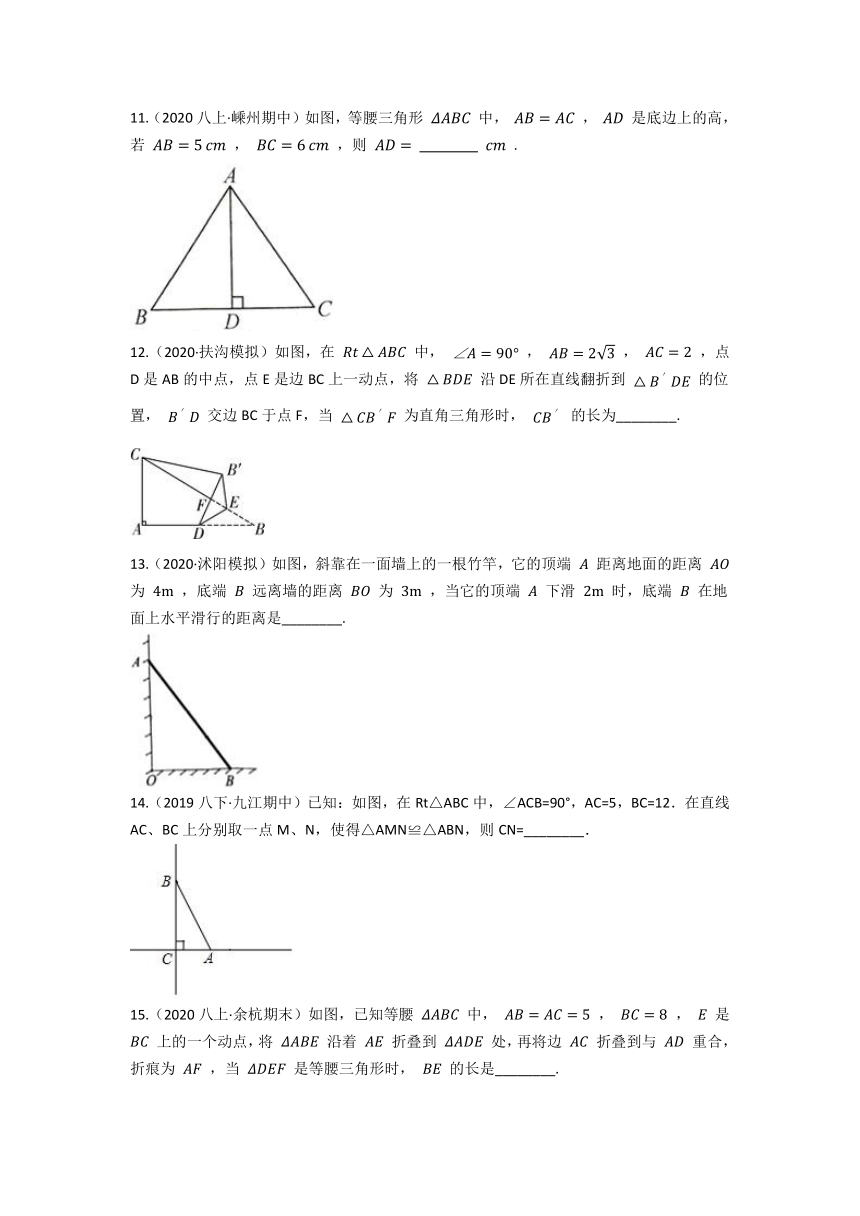
7.(2021·南海模拟)将一枚飞镖投掷到如图所示的正六边形镖盘上(每次飞镖均落在镖盘上,且落在镖盘的任何一个点的机会都相等),飞镖落在阴影区域的概率为( )
A. B. C. D.
8.代数式 的最小值为( )
A. 12 B. 13 C. 14 D. 11
9.(2019八上·大庆期末)如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )
A. B. C. D.
10.(2021·南湖模拟)如图,矩形纸片 中, , 是 上一点,连结 , 沿直线 翻折后点 落到点 ,过点 作 ,垂足为 .若 ,则 的值为( )
A. B. C. D.
二、填空题
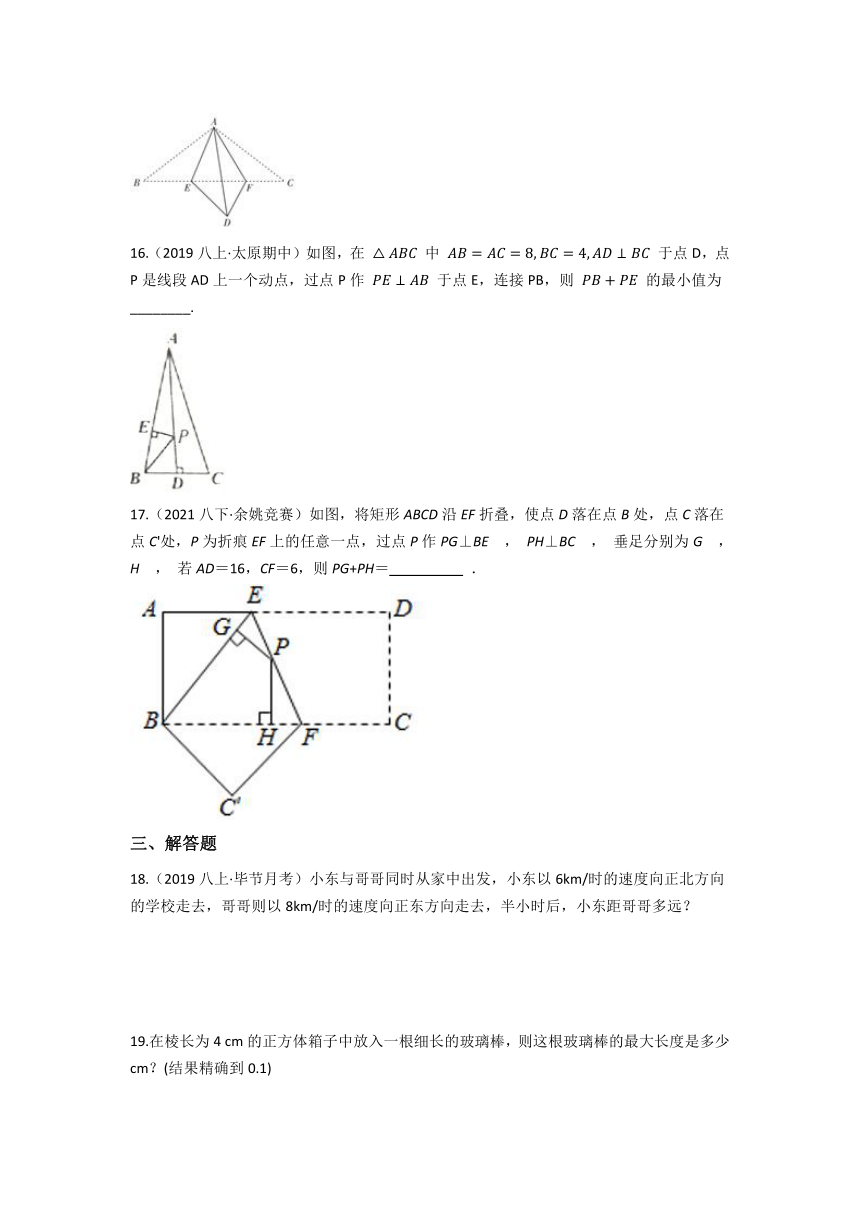
11.(2020八上·嵊州期中)如图,等腰三角形 中, , 是底边上的高,若 , ,则 .
12.(2020·扶沟模拟)如图,在 中, , , ,点D是AB的中点,点E是边BC上一动点,将 沿DE所在直线翻折到 的位置, 交边BC于点F,当 为直角三角形时, 的长为________.
13.(2020·沭阳模拟)如图,斜靠在一面墙上的一根竹竿,它的顶端 距离地面的距离 为 ,底端 远离墙的距离 为 ,当它的顶端 下滑 时,底端 在地面上水平滑行的距离是________.
14.(2019八下·九江期中)已知:如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12.在直线AC、BC上分别取一点M、N,使得△AMN≌△ABN,则CN=________.
15.(2020八上·余杭期末)如图,已知等腰 中, , , 是 上的一个动点,将 沿着 折叠到 处,再将边 折叠到与 重合,折痕为 ,当 是等腰三角形时, 的长是________.
16.(2019八上·太原期中)如图,在 中 于点D,点P是线段AD上一个动点,过点P作 于点E,连接PB,则 的最小值为________.
17.(2021八下·余姚竞赛)如图,将矩形ABCD沿EF折叠,使点D落在点B处,点C落在点C'处,P为折痕EF上的任意一点,过点P作PG⊥BE , PH⊥BC , 垂足分别为G , H , 若AD=16,CF=6,则PG+PH= .
三、解答题
18.(2019八上·毕节月考)小东与哥哥同时从家中出发,小东以6km/时的速度向正北方向的学校走去,哥哥则以8km/时的速度向正东方向走去,半小时后,小东距哥哥多远?
19.在棱长为4 cm的正方体箱子中放入一根细长的玻璃棒,则这根玻璃棒的最大长度是多少cm?(结果精确到0.1)
20.为了推广城市绿色出行,某市准备在AB路段建设一个共享单车停放点,该路段附近有两个广场C和D,如图所示,CA⊥AB于点A,DB⊥AB于点B,AB=1 700 m,CA=1 200m,DB=500m,试问这个单车停放点E应建在距点A多远处,才能使它到两广场的距离相等?
21.(2020七下·津南月考)如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,求点P的坐标.
22.(2020八上·东台月考)如图,在平面直角坐标系中长方形ABCO的顶点A,C的坐标分别为(0,8) ,(20,0),D是OC的中点,点P在AB上运动,当△ODP是腰长为10的等腰三角形时,求点P的坐标.
23.(2020八下·邯郸月考)如图,将矩形ABCD沿EF折叠,使点C恰好落在AB边的中点C'上,点D落在D'处,C'D'交AE于点M.若AB=6,BC=9,求线段ED.
答案解析部分
一、单选题
1.【答案】 C
【考点】三角形内角和定理,勾股定理的逆定理
【解析】【解答】解:(1)∵一个内角等于另外两个内角之差,∴∠A=∠B﹣∠C,∵∠A+∠B+∠C=180°,
∴∠B=90°,故是直角三角形;
( 2 )∵三个内角度数之比为3:4:5;∴设较小的角为3x,则其于两角为4x,5x,则三个角分别为45°,60°,75°,故不是直角三角形;
( 3 )因为三边符合勾股定理的逆定理,故是直角三角形;
( 4 )因为三边符合勾股定理的逆定理,故是直角三角形.
所以有三个直角三角形,故答案为:C.
【分析】(1)(2)由题意结合三角形内角和定理可求得三角形内角的度数,从而根据直角三角形的定义即可判断求解;
(3)(4)由题意结合勾股定理的逆定理即可判断求解.
2.【答案】 B
【考点】勾股定理,矩形的性质
【解析】【解答】解:如图,
矩形ABCD中,∠BAD=90°,AB=5,AD=12,∴ 13,∴AC=BD=13.
故答案为:B.
【分析】由勾股定理可求出BD长,由矩形的性质可得AC=BD=13.
3.【答案】 D
【考点】勾股定理
【解析】【解答】如图,连接AD
由题意得:
故答案为:D.
【分析】如图(见解析),先根据正方形的边长、圆的性质可得AD、CE、AE的长,再根据勾股定理可求出DE的长,然后根据线段的和差即可得.
4.【答案】 D
【考点】勾股定理,矩形的性质
【解析】【解答】解:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,
由折叠的性质得:∠AFE=∠D=90°,EF=ED , AF=AD ,
∴tan∠EFC= = ,
设CE=3k , 则CF=4k ,
由勾股定理得DE=EF= =5k ,
∴DC=AB=8k ,
∵∠AFB+∠BAF=90°,∠AFB+∠EFC=90°,
∴∠BAF=∠EFC ,
∴tan∠BAF= =tan∠EFC= ,
∴BF=6k , AF=BC=AD=10k ,
在Rt△AFE中,由勾股定理得AE= = =5 k=5 ,
解得:k=1,
∴矩形ABCD的周长=2(AB+BC)=2(8k+10k)=36(cm),
故答案为:D .
【分析】先求出tan∠EFC= = ,再利用勾股定理求出AE=5 ,最后计算求解即可。
5.【答案】 B
【考点】勾股定理的应用
【解析】【解答】解:设大正方形的边长为c,则c2=20,小正方形的面积(a b)2=4,
∵a2+b2=c2=20,(a b)2=4,
∴a2+b2 2ab=4,即20 2ab=4.
∴ab=8.
故答案为:B.
【分析】
6.【答案】 D
【考点】勾股定理的应用,矩形的性质,翻折变换(折叠问题)
【解析】【解答】当△CEB′为直角三角形时,有两种情况:
①当点B′落在矩形内部时,如答图1所示。
连结AC,
在Rt△ABC中,AB=3,BC=4,
∴AC=
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A. B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,
∴EB=EB′,AB=AB′=3,
∴CB′=5 3=2,
设BE=x,则EB′=x,CE=4 x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2 ,
∴x2+22=(4 x)2,解得x= ,
∴BE= ;
②当点B′落在AD边上时,如答图2所示。
此时ABEB′为正方形,
∴BE=AB=3.
综上所述,BE的长为 或3.
故答案为:D.
【分析】当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如答图1所示.连结AC,先利用勾股定理计算出AC=5,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=3,可计算出CB′=2,设BE=x,则EB′=x,CE=4-x,然后在Rt△CEB′中运用勾股定理可计算出x.②当点B′落在AD边上时,如答图2所示.此时ABEB′为正方形.
7.【答案】 B
【考点】勾股定理,概率公式
【解析】【解答】解:设正六边形的边长为a , 过A作AG⊥BF , 垂足为G , 如图,
∵六边形ABCDEF是正六边形,
∴AF=AB=BC=CD=DE=EF ,
∴
∴
∴
∴由勾股定理得FG= ,
∴BF=
∴
∴白色部分的面积 ,阴影区域的面积是a× a= a2 ,
所以正六边形的面积为
则飞镖落在阴影区域的概率为 .
故答案为:B .
【分析】利用阴影部分的面积除以正六边形的面积,求出答案即可。
8.【答案】 B
【考点】线段的性质:两点之间线段最短,勾股定理的应用
【解析】【解答】解:如图所示:
设P点坐标为P(x,0),
原式可化为 + ,
即 =AP, =BP,
AB= =13.
代数式 的最小值为13.
故答案为:B.
【分析】设P点坐标为P(x,0),根据两点间的距离公式,原式可化为 + ,即 =AP, =BP,只有当A、B、P三点在同一直线上的时候,AB=AP+BP最小,根据勾股定理算出AB的长从而得出答案。
9.【答案】 B
【考点】勾股定理,矩形的性质,翻折变换(折叠问题)
【解析】【解答】连接BF,由折叠可知AE垂直平分BF,
∵BC=6,点E为BC的中点,
∴BE=3,
又∵AB=4,
∴AE= =5,
∵ ,
∴ ,
∴BH= ,则BF= ,
∵FE=BE=EC,
∴∠BFC=90°,
∴CF= = .
故答案为:B.
【分析】连接BF,由折叠可知AE垂直平分BF,根据勾股定理求得AE=5,利用直角三角形面积的两种表示法求得BH= ,即可得BF= ,再证明∠BFC=90°,最后利用勾股定理求得CF= .
10.【答案】 C
【考点】勾股定理,矩形的性质,翻折变换(折叠问题)
【解析】【解答】如图,作 于点H.
∵AD=6,AD=3GD,
∴GD=2,AG=4.
由题意可知AF=AD=6,EF=DE.
∴在 中, .
由所作辅助线可知四边形 为矩形,
∴HE=GD=2, .
设 ,则 ,
∴ .
∴在 中, ,即 ,
解得: .
故 .
故答案为:C.
【分析】作 于点H,根据折叠的性质,结合题意求出AF和AG的长,然后根据勾股定理求出GF,设 ,然后把相关线段用含x的代数式表示,在 中,根据勾股定理构建方程求解,即可解答.
二、填空题
11.【答案】 4
【考点】等腰三角形的性质,勾股定理
【解析】【解答】解:∵等腰三角形 中, , 是底边上的高,
∴AD是△ABC中BC边上的中线,
∴BD=DC,
∵ ,
∴DB=3cm,
∵ ,
∴ ,
故答案为:4.
【分析】根据等腰三角形的三线合一,可知BD=3,在直角三角形ABD中利用勾股定理,即可求得AD的长.
12.【答案】 或2
【考点】全等三角形的判定与性质,勾股定理,翻折变换(折叠问题)
【解析】【解答】解:∵在 中, , , , ,∵点 为 的中点, ,
①如解图①,
图①
当 时, , ,
, ,
;
②如解图②,连接 ,
图②
当 时,
, , ,
,
.综上所述, 的长为 或2.
故答案为: 或2 .
【分析】由题意可分两种情况讨论求解:①当∠CFB =90°时,根据30度角的直角三角形的性质可知∠B=30°,且DF=BD,则B F的值可求解,于是根据线段的构成得CF=BC-BF,于是在直角三角形CB F中,用勾股定理可求得CB 的长;②当CB F=90时,易证CDA△≌△CDB ,则CB =CA可求解.综合两种情况可求解.
13.【答案】 ( )m
【考点】勾股定理的应用
【解析】【解答】解:如图,根据题意有AC=2,OA=4,OB=3,AB=CD,BD即为所求.
∵OA=4,OB=3
∴
∵AC=2,
∴
∴
∴
故答案为:( )m.
【分析】先根据题意作出图形,然后先利用勾股定理求出AB的长度,然后再利用勾股定理求出OD的长度,从而可得到BD的长度.
14.【答案】 或 .
【考点】三角形全等的判定,勾股定理
【解析】【解答】①如图1所示:
若△AMN≌△ABN,则BN=MN,且AM=AB=13,∴CM=8,
设CN=x,在Rt△MCN中,MC2+CN2=MN2 , 即82+x2=(12–x)2 ,
解得x= ,∴CN= ;
②如图2所示:
若△AMN≌△ABN,则BN=MN,且AM=AB=13,∴CM=18,
设CN=x,则BN=MN=x+12,
在Rt△MCN中,MC2+CN2=MN2 ,
即182+x2=(12+x)2 , 解得x= ,∴CN= ;
综上所述:CN的长为 或 .
故答案为 或 .
【分析】分两种情况:①当∠BAN=∠MAN,且AM=AB时,则BN=MN,且AM=AB=13,求出CM,设CN=x,在Rt△MCN中,由勾股定理得出方程,解方程即可;
②当∠BAN=∠MAN,且AM=AB时,则BN=MN,且AM=AB=13,求出CM=18,设CN=x,则BN=MN=x+12,在Rt△MCN中,由勾股定理得出方程,解方程即可.
15.【答案】 , ,
【考点】三角形全等的判定,等腰三角形的性质,勾股定理,翻折变换(折叠问题)
【解析】【解答】解:由折叠可知:∠B=∠ADE, ∠C=∠ADF,AB=AD=5,AC=AD=5,BE=ED,DF=FC
过A作AM⊥BC于M
∵AB=AC
∴BM=CM= BC=4,∠B=∠C
∴∠B=∠ADE=∠C=∠ADF
由勾股定理可知:
①当DE=DF=a时,
则BE=ED=DF=FC=a,EM=BM-BE=4-x
∵∠ADE=∠ADF
∴AD⊥BC
又∵AM⊥BC
∴A、M、D三点共线,∠EMD=90°
∴DM=AD-AM=5-3=2
在Rt△EMD中:
∴
解得:
②当DE=EF时,
∵BE=ED
∴BE=EF
连接BD,延长AE交BD于G
∵AB=AD,BE=ED
∴AG垂直平分BD
∴BG=DG
设EM=b则BE=EF=4-b
∴FC=8-(8-2b)=2b
∴FD=FC=2b
在△BMD中: BG=DG,BE=EF
∴EG是△BMD的中位线
∴
∴GE=EM=b
∵∠BME=∠AHE=90°,∠BEG=∠AEM
∴
∴BG=AM=3
在Rt△BEG中:
∴
∴
∴BE=4-
③当DF=EF时,
∵CF=DF
∴CF=EF
连接CD,延长AF交CD于H
∵AC=AD,DF=FC
∴AH垂直平分CD
∴DH=CH
设FM=c则FC=FD=4-c
∴BE=8-(8-2c)=2c
∴BE=ED=2c
在△ECD中: EF=FC,DH=HC
∴FH是△ECD的中位线
∴
∴FH=FM=c
∵∠AMF=∠CHF=90°,∠AFM=∠CFH
∴
∴CH=AM=3
在Rt△FCH中:
∴
∴
∴BE=
故答案为: , ,
【分析】分DE=DF,EF=ED,EF=FD,三种情况进行讨论,结合等腰三角形的性质及全等三角形判定和性质即可解决.
16.【答案】
【考点】等腰三角形的性质,勾股定理,轴对称的应用-最短距离问题
【解析】【解答】∵
∴点B与点C关于AD对称
过点C作CE⊥AB于一点即为点P,此时 最小
∵
∴BD=2
在Rt△ABC中,
∵S△ABC=
∴
得
故此题填
【分析】根据题意点B与点C关于AD对称,所以过点C作AB的垂线,与AD的交点即点P,求出CE即可得到答案
17.【答案】 8
【考点】勾股定理,矩形的性质,翻折变换(折叠问题)
【解析】【解答】解:过点E作EQ⊥BC于点Q,连接BP,如图所示:
、
∵四边形ABCD为矩形,
∴AD=BC,AD∥BC,∠C=90°,
∴∠DEF=∠EFB,
由折叠可知∠BEF=∠FED,C'F=CF,BC=CD,∠C=∠C'=90°,
∴BE=BF,
∴ ,
∴EQ=PG+PH ,
∵ AD=16,CF=6,
∴BF=BC-CF=AD-CF=10,
在Rt△BC'F中,由勾股定理得 ,
∴CD=8,
∵AD∥BC,EQ⊥BC,
∴EQ=PG+PH=8 ,
故答案为:8.
【分析】过点E作EQ⊥BC于点Q,连接BP,先由矩形的性质即可求出AD=BC,AD∥BC,∠C=90°,进而得到∠DEF=∠EFB,再由折叠的性质即可得到∠BEF=∠FED,C'F=CF,BC=CD,∠C=∠C'=90°,进而得到BE=BF,运用等面积法表示△BEF的面积即可得到EQ=PG+PH ,在Rt△BC'F中,依据勾股定理即可求出BC'的长,进而可以求解.
三、解答题
18.【答案】 解:由题意得,AC=6× =3km,BC=8× =4km,∠ACB=90°,
则AB= =5km.
【考点】勾股定理的应用
【解析】【分析】据题意求出小东与哥哥各自行走的距离,根据勾股定理计算即可.
19.【答案】 解:如图 ,玻璃棒最大长度为正方体的体对角线AC的长,
因为BC2 =BD2+CD2 =42+42=32,
所以AC2 =AB2+BC2 =42+32= 48.
因为6.922≈47.886, 6.932≈48.025,
所以6.92 cm答:玻璃棒的最大长度为6.9 cm.
【考点】勾股定理
【解析】【分析】要运用两次勾股定理,首先求得底面的对角线,在利用勾股定理即可求解。
20.【答案】 解:设AE=x m时,它到两广场的距离相等,
则BE=(1 700- x)m,
由题意得1 2002+x2=(1 700-x)2+ 5002 ,
解得x=500.
答:这个单车停放点E应建在距点A500 m处,它到两广场的距离相等.
【考点】勾股定理的应用
【解析】【分析】设AE的长度为x,根据其到两个广场的距离相等列出方程,解方程得到答案即可。
21.【答案】 解:(1)OD是等腰三角形的底边时,P就是OD的垂直平分线与CB的交点,此时OP=PD≠5;
(2)OD是等腰三角形的一条腰时:
①若点O是顶角顶点时,P点就是以点O为圆心,以5为半径的弧与CB的交点,
在直角△OPC中,CP= =3,则P的坐标是(3,4);
②若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,
过D作DM⊥BC于点M,
在直角△PDM中,PM= =3,
当P在M的左边时,CP=5-3=2,则P的坐标是(2,4);
当P在M的右侧时,CP=5+3=8,则P的坐标是(8,4).
故P的坐标为:(3,4)或(2,4)或(8,4).
【考点】勾股定理,矩形的性质
【解析】【分析】分类讨论,利用勾股定理进行求解即可。
22.【答案】 解:∵A(0,8),C(20,0),四边形OABC是矩形,D是OC的中点,
∴OA=8,OD=10,∠OAB=∠COA= ,
①当OP=OD=10时,
过点P作PE⊥OC轴于点E,则PE=8.
在Rt△PEO中,由勾股定理得:OE= ,
即P点的坐标是(6,8);
②当DP=OD=10时,
过P作PE⊥OC于E,
则PE=OA=8,
由勾股定理得:DE= ,
OE=10-6=4,
即P点坐标是(4,8);
③当OP=DP=10时,
由勾股定理得:DE=OE= ,
即OD=DE+OE=12≠10,即此时不存在;
④当OD=PD时,
过点P作PE⊥OC轴于点E,则PE=8
在Rt△PED中,由勾股定理得:DE= ,
∴OE=OD+DE=10+6=16
∴此时点P坐标为(16,8).
故P点的坐标为:(6,8)或(4,8)或(16,8).
【考点】等腰三角形的性质,勾股定理,矩形的性质
【解析】【分析】由点A、C的坐标以及矩形的性质可得OA=8,OD=10,∠OAB=∠COA=90°,①当OP=OD=10时,过点P作PE⊥OC轴于点E,则PE=8,在Rt△PEO中,由勾股定理求得OE,据此可得点P的坐标;②当DP=OD=10时,过P作PE⊥OC于E,则PE=OA=8,由勾股定理求出DE,进而得OE,据此可得点P的坐标;③当OP=DP=10时,由勾股定理得:DE=OE=6,求出OD,判断出此种情况不存在;④当OD=PD时,过点P作PE⊥OC轴于点E,则PE=8,在Rt△PED中,由勾股定理求得DE,进而求出OE,据此可得点P的坐标.
23.【答案】 解:如图,连接C'E,
设DE=D'E=x,
∵在矩形ABCD中,AB=6,BC=9,
∴CD=AB=6,AD=BC=9,∠A=∠D=90°,
∴AE=AD-DE=9-x,
∵折叠,
∴∠D'=∠D=90°,C'D'=CD=6,
∵点C'为AB边的中点,
∴AC'= AB=3,
在Rt△AEC'中,C'E2=AE2+AC'2=32+(9-x)2 ,
在Rt△C'D'E中,C'E2=C'D'2+D'E2=62+x2 ,
∴32+(9-x)2=62+x2 ,
解得x=3,
∴线段ED的长为3.
【考点】勾股定理
【解析】【分析】连接C'E,设DE=D'E=x,则AE=9-x,利用两次勾股定理分别表示出C'E2 , 进而得到方程求解即可.
勾股定理
一、单选题
1.(2019八下·南岸期中)有四个三角形,分别满足下列条件,其中直角三角形有( )
( 1 )一个内角等于另外两个内角之差:(2)三个内角度数之比为3:4:5;(3)三边长度之比为5:12:13;(4)三边长分别为7、24、25.
A. 1个 B. 2个 C. 3个 D. 4个
2.(2019八下·丹江口期末)矩形ABCD中,已知AB=5,AD=12,则AC长为( )
A. 9 B. 13 C. 17 D. 20
3.(2020八下·江夏月考)如图,网格中每个小正方形的边长均为1,点A,B,C都在格点上,以A为圆心,AB为半径画弧,交最上方的网格线于点D,则图中线段CD的长是( )
A. 0.8 B. C. D. 3-
4.(2020·昆明模拟)如图,折叠矩形ABCD的一边AD , 使点D落在BC边的点F处,已知折痕AE=5 cm , 且tan∠EFC= ,那么矩形ABCD的周长为( )
A. 18 B. 25 C. 32 D. 36
5.(2020八上·盐城期中)如图,在赵爽弦图中,已知直角三角形的短直角边长为a,长直角边长为b,大正方形的面积为20,小正方形的面积为4,则 的值是( )
A. 10 B. 8 C. 7 D. 5
6.(2019八下·武安期末)如图,矩形 中, , ,点 是 边上一点,连接 ,把 沿 折叠,使点 落在点 处,当 为直角三角形时, 的长为( )
A. 3 B. C. 2或3 D. 3或
7.(2021·南海模拟)将一枚飞镖投掷到如图所示的正六边形镖盘上(每次飞镖均落在镖盘上,且落在镖盘的任何一个点的机会都相等),飞镖落在阴影区域的概率为( )
A. B. C. D.
8.代数式 的最小值为( )
A. 12 B. 13 C. 14 D. 11
9.(2019八上·大庆期末)如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )
A. B. C. D.
10.(2021·南湖模拟)如图,矩形纸片 中, , 是 上一点,连结 , 沿直线 翻折后点 落到点 ,过点 作 ,垂足为 .若 ,则 的值为( )
A. B. C. D.
二、填空题
11.(2020八上·嵊州期中)如图,等腰三角形 中, , 是底边上的高,若 , ,则 .
12.(2020·扶沟模拟)如图,在 中, , , ,点D是AB的中点,点E是边BC上一动点,将 沿DE所在直线翻折到 的位置, 交边BC于点F,当 为直角三角形时, 的长为________.
13.(2020·沭阳模拟)如图,斜靠在一面墙上的一根竹竿,它的顶端 距离地面的距离 为 ,底端 远离墙的距离 为 ,当它的顶端 下滑 时,底端 在地面上水平滑行的距离是________.
14.(2019八下·九江期中)已知:如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12.在直线AC、BC上分别取一点M、N,使得△AMN≌△ABN,则CN=________.
15.(2020八上·余杭期末)如图,已知等腰 中, , , 是 上的一个动点,将 沿着 折叠到 处,再将边 折叠到与 重合,折痕为 ,当 是等腰三角形时, 的长是________.
16.(2019八上·太原期中)如图,在 中 于点D,点P是线段AD上一个动点,过点P作 于点E,连接PB,则 的最小值为________.
17.(2021八下·余姚竞赛)如图,将矩形ABCD沿EF折叠,使点D落在点B处,点C落在点C'处,P为折痕EF上的任意一点,过点P作PG⊥BE , PH⊥BC , 垂足分别为G , H , 若AD=16,CF=6,则PG+PH= .
三、解答题
18.(2019八上·毕节月考)小东与哥哥同时从家中出发,小东以6km/时的速度向正北方向的学校走去,哥哥则以8km/时的速度向正东方向走去,半小时后,小东距哥哥多远?
19.在棱长为4 cm的正方体箱子中放入一根细长的玻璃棒,则这根玻璃棒的最大长度是多少cm?(结果精确到0.1)
20.为了推广城市绿色出行,某市准备在AB路段建设一个共享单车停放点,该路段附近有两个广场C和D,如图所示,CA⊥AB于点A,DB⊥AB于点B,AB=1 700 m,CA=1 200m,DB=500m,试问这个单车停放点E应建在距点A多远处,才能使它到两广场的距离相等?
21.(2020七下·津南月考)如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,求点P的坐标.
22.(2020八上·东台月考)如图,在平面直角坐标系中长方形ABCO的顶点A,C的坐标分别为(0,8) ,(20,0),D是OC的中点,点P在AB上运动,当△ODP是腰长为10的等腰三角形时,求点P的坐标.
23.(2020八下·邯郸月考)如图,将矩形ABCD沿EF折叠,使点C恰好落在AB边的中点C'上,点D落在D'处,C'D'交AE于点M.若AB=6,BC=9,求线段ED.
答案解析部分
一、单选题
1.【答案】 C
【考点】三角形内角和定理,勾股定理的逆定理
【解析】【解答】解:(1)∵一个内角等于另外两个内角之差,∴∠A=∠B﹣∠C,∵∠A+∠B+∠C=180°,
∴∠B=90°,故是直角三角形;
( 2 )∵三个内角度数之比为3:4:5;∴设较小的角为3x,则其于两角为4x,5x,则三个角分别为45°,60°,75°,故不是直角三角形;
( 3 )因为三边符合勾股定理的逆定理,故是直角三角形;
( 4 )因为三边符合勾股定理的逆定理,故是直角三角形.
所以有三个直角三角形,故答案为:C.
【分析】(1)(2)由题意结合三角形内角和定理可求得三角形内角的度数,从而根据直角三角形的定义即可判断求解;
(3)(4)由题意结合勾股定理的逆定理即可判断求解.
2.【答案】 B
【考点】勾股定理,矩形的性质
【解析】【解答】解:如图,
矩形ABCD中,∠BAD=90°,AB=5,AD=12,∴ 13,∴AC=BD=13.
故答案为:B.
【分析】由勾股定理可求出BD长,由矩形的性质可得AC=BD=13.
3.【答案】 D
【考点】勾股定理
【解析】【解答】如图,连接AD
由题意得:
故答案为:D.
【分析】如图(见解析),先根据正方形的边长、圆的性质可得AD、CE、AE的长,再根据勾股定理可求出DE的长,然后根据线段的和差即可得.
4.【答案】 D
【考点】勾股定理,矩形的性质
【解析】【解答】解:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,
由折叠的性质得:∠AFE=∠D=90°,EF=ED , AF=AD ,
∴tan∠EFC= = ,
设CE=3k , 则CF=4k ,
由勾股定理得DE=EF= =5k ,
∴DC=AB=8k ,
∵∠AFB+∠BAF=90°,∠AFB+∠EFC=90°,
∴∠BAF=∠EFC ,
∴tan∠BAF= =tan∠EFC= ,
∴BF=6k , AF=BC=AD=10k ,
在Rt△AFE中,由勾股定理得AE= = =5 k=5 ,
解得:k=1,
∴矩形ABCD的周长=2(AB+BC)=2(8k+10k)=36(cm),
故答案为:D .
【分析】先求出tan∠EFC= = ,再利用勾股定理求出AE=5 ,最后计算求解即可。
5.【答案】 B
【考点】勾股定理的应用
【解析】【解答】解:设大正方形的边长为c,则c2=20,小正方形的面积(a b)2=4,
∵a2+b2=c2=20,(a b)2=4,
∴a2+b2 2ab=4,即20 2ab=4.
∴ab=8.
故答案为:B.
【分析】
6.【答案】 D
【考点】勾股定理的应用,矩形的性质,翻折变换(折叠问题)
【解析】【解答】当△CEB′为直角三角形时,有两种情况:
①当点B′落在矩形内部时,如答图1所示。
连结AC,
在Rt△ABC中,AB=3,BC=4,
∴AC=
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A. B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,
∴EB=EB′,AB=AB′=3,
∴CB′=5 3=2,
设BE=x,则EB′=x,CE=4 x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2 ,
∴x2+22=(4 x)2,解得x= ,
∴BE= ;
②当点B′落在AD边上时,如答图2所示。
此时ABEB′为正方形,
∴BE=AB=3.
综上所述,BE的长为 或3.
故答案为:D.
【分析】当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如答图1所示.连结AC,先利用勾股定理计算出AC=5,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=3,可计算出CB′=2,设BE=x,则EB′=x,CE=4-x,然后在Rt△CEB′中运用勾股定理可计算出x.②当点B′落在AD边上时,如答图2所示.此时ABEB′为正方形.
7.【答案】 B
【考点】勾股定理,概率公式
【解析】【解答】解:设正六边形的边长为a , 过A作AG⊥BF , 垂足为G , 如图,
∵六边形ABCDEF是正六边形,
∴AF=AB=BC=CD=DE=EF ,
∴
∴
∴
∴由勾股定理得FG= ,
∴BF=
∴
∴白色部分的面积 ,阴影区域的面积是a× a= a2 ,
所以正六边形的面积为
则飞镖落在阴影区域的概率为 .
故答案为:B .
【分析】利用阴影部分的面积除以正六边形的面积,求出答案即可。
8.【答案】 B
【考点】线段的性质:两点之间线段最短,勾股定理的应用
【解析】【解答】解:如图所示:
设P点坐标为P(x,0),
原式可化为 + ,
即 =AP, =BP,
AB= =13.
代数式 的最小值为13.
故答案为:B.
【分析】设P点坐标为P(x,0),根据两点间的距离公式,原式可化为 + ,即 =AP, =BP,只有当A、B、P三点在同一直线上的时候,AB=AP+BP最小,根据勾股定理算出AB的长从而得出答案。
9.【答案】 B
【考点】勾股定理,矩形的性质,翻折变换(折叠问题)
【解析】【解答】连接BF,由折叠可知AE垂直平分BF,
∵BC=6,点E为BC的中点,
∴BE=3,
又∵AB=4,
∴AE= =5,
∵ ,
∴ ,
∴BH= ,则BF= ,
∵FE=BE=EC,
∴∠BFC=90°,
∴CF= = .
故答案为:B.
【分析】连接BF,由折叠可知AE垂直平分BF,根据勾股定理求得AE=5,利用直角三角形面积的两种表示法求得BH= ,即可得BF= ,再证明∠BFC=90°,最后利用勾股定理求得CF= .
10.【答案】 C
【考点】勾股定理,矩形的性质,翻折变换(折叠问题)
【解析】【解答】如图,作 于点H.
∵AD=6,AD=3GD,
∴GD=2,AG=4.
由题意可知AF=AD=6,EF=DE.
∴在 中, .
由所作辅助线可知四边形 为矩形,
∴HE=GD=2, .
设 ,则 ,
∴ .
∴在 中, ,即 ,
解得: .
故 .
故答案为:C.
【分析】作 于点H,根据折叠的性质,结合题意求出AF和AG的长,然后根据勾股定理求出GF,设 ,然后把相关线段用含x的代数式表示,在 中,根据勾股定理构建方程求解,即可解答.
二、填空题
11.【答案】 4
【考点】等腰三角形的性质,勾股定理
【解析】【解答】解:∵等腰三角形 中, , 是底边上的高,
∴AD是△ABC中BC边上的中线,
∴BD=DC,
∵ ,
∴DB=3cm,
∵ ,
∴ ,
故答案为:4.
【分析】根据等腰三角形的三线合一,可知BD=3,在直角三角形ABD中利用勾股定理,即可求得AD的长.
12.【答案】 或2
【考点】全等三角形的判定与性质,勾股定理,翻折变换(折叠问题)
【解析】【解答】解:∵在 中, , , , ,∵点 为 的中点, ,
①如解图①,
图①
当 时, , ,
, ,
;
②如解图②,连接 ,
图②
当 时,
, , ,
,
.综上所述, 的长为 或2.
故答案为: 或2 .
【分析】由题意可分两种情况讨论求解:①当∠CFB =90°时,根据30度角的直角三角形的性质可知∠B=30°,且DF=BD,则B F的值可求解,于是根据线段的构成得CF=BC-BF,于是在直角三角形CB F中,用勾股定理可求得CB 的长;②当CB F=90时,易证CDA△≌△CDB ,则CB =CA可求解.综合两种情况可求解.
13.【答案】 ( )m
【考点】勾股定理的应用
【解析】【解答】解:如图,根据题意有AC=2,OA=4,OB=3,AB=CD,BD即为所求.
∵OA=4,OB=3
∴
∵AC=2,
∴
∴
∴
故答案为:( )m.
【分析】先根据题意作出图形,然后先利用勾股定理求出AB的长度,然后再利用勾股定理求出OD的长度,从而可得到BD的长度.
14.【答案】 或 .
【考点】三角形全等的判定,勾股定理
【解析】【解答】①如图1所示:
若△AMN≌△ABN,则BN=MN,且AM=AB=13,∴CM=8,
设CN=x,在Rt△MCN中,MC2+CN2=MN2 , 即82+x2=(12–x)2 ,
解得x= ,∴CN= ;
②如图2所示:
若△AMN≌△ABN,则BN=MN,且AM=AB=13,∴CM=18,
设CN=x,则BN=MN=x+12,
在Rt△MCN中,MC2+CN2=MN2 ,
即182+x2=(12+x)2 , 解得x= ,∴CN= ;
综上所述:CN的长为 或 .
故答案为 或 .
【分析】分两种情况:①当∠BAN=∠MAN,且AM=AB时,则BN=MN,且AM=AB=13,求出CM,设CN=x,在Rt△MCN中,由勾股定理得出方程,解方程即可;
②当∠BAN=∠MAN,且AM=AB时,则BN=MN,且AM=AB=13,求出CM=18,设CN=x,则BN=MN=x+12,在Rt△MCN中,由勾股定理得出方程,解方程即可.
15.【答案】 , ,
【考点】三角形全等的判定,等腰三角形的性质,勾股定理,翻折变换(折叠问题)
【解析】【解答】解:由折叠可知:∠B=∠ADE, ∠C=∠ADF,AB=AD=5,AC=AD=5,BE=ED,DF=FC
过A作AM⊥BC于M
∵AB=AC
∴BM=CM= BC=4,∠B=∠C
∴∠B=∠ADE=∠C=∠ADF
由勾股定理可知:
①当DE=DF=a时,
则BE=ED=DF=FC=a,EM=BM-BE=4-x
∵∠ADE=∠ADF
∴AD⊥BC
又∵AM⊥BC
∴A、M、D三点共线,∠EMD=90°
∴DM=AD-AM=5-3=2
在Rt△EMD中:
∴
解得:
②当DE=EF时,
∵BE=ED
∴BE=EF
连接BD,延长AE交BD于G
∵AB=AD,BE=ED
∴AG垂直平分BD
∴BG=DG
设EM=b则BE=EF=4-b
∴FC=8-(8-2b)=2b
∴FD=FC=2b
在△BMD中: BG=DG,BE=EF
∴EG是△BMD的中位线
∴
∴GE=EM=b
∵∠BME=∠AHE=90°,∠BEG=∠AEM
∴
∴BG=AM=3
在Rt△BEG中:
∴
∴
∴BE=4-
③当DF=EF时,
∵CF=DF
∴CF=EF
连接CD,延长AF交CD于H
∵AC=AD,DF=FC
∴AH垂直平分CD
∴DH=CH
设FM=c则FC=FD=4-c
∴BE=8-(8-2c)=2c
∴BE=ED=2c
在△ECD中: EF=FC,DH=HC
∴FH是△ECD的中位线
∴
∴FH=FM=c
∵∠AMF=∠CHF=90°,∠AFM=∠CFH
∴
∴CH=AM=3
在Rt△FCH中:
∴
∴
∴BE=
故答案为: , ,
【分析】分DE=DF,EF=ED,EF=FD,三种情况进行讨论,结合等腰三角形的性质及全等三角形判定和性质即可解决.
16.【答案】
【考点】等腰三角形的性质,勾股定理,轴对称的应用-最短距离问题
【解析】【解答】∵
∴点B与点C关于AD对称
过点C作CE⊥AB于一点即为点P,此时 最小
∵
∴BD=2
在Rt△ABC中,
∵S△ABC=
∴
得
故此题填
【分析】根据题意点B与点C关于AD对称,所以过点C作AB的垂线,与AD的交点即点P,求出CE即可得到答案
17.【答案】 8
【考点】勾股定理,矩形的性质,翻折变换(折叠问题)
【解析】【解答】解:过点E作EQ⊥BC于点Q,连接BP,如图所示:
、
∵四边形ABCD为矩形,
∴AD=BC,AD∥BC,∠C=90°,
∴∠DEF=∠EFB,
由折叠可知∠BEF=∠FED,C'F=CF,BC=CD,∠C=∠C'=90°,
∴BE=BF,
∴ ,
∴EQ=PG+PH ,
∵ AD=16,CF=6,
∴BF=BC-CF=AD-CF=10,
在Rt△BC'F中,由勾股定理得 ,
∴CD=8,
∵AD∥BC,EQ⊥BC,
∴EQ=PG+PH=8 ,
故答案为:8.
【分析】过点E作EQ⊥BC于点Q,连接BP,先由矩形的性质即可求出AD=BC,AD∥BC,∠C=90°,进而得到∠DEF=∠EFB,再由折叠的性质即可得到∠BEF=∠FED,C'F=CF,BC=CD,∠C=∠C'=90°,进而得到BE=BF,运用等面积法表示△BEF的面积即可得到EQ=PG+PH ,在Rt△BC'F中,依据勾股定理即可求出BC'的长,进而可以求解.
三、解答题
18.【答案】 解:由题意得,AC=6× =3km,BC=8× =4km,∠ACB=90°,
则AB= =5km.
【考点】勾股定理的应用
【解析】【分析】据题意求出小东与哥哥各自行走的距离,根据勾股定理计算即可.
19.【答案】 解:如图 ,玻璃棒最大长度为正方体的体对角线AC的长,
因为BC2 =BD2+CD2 =42+42=32,
所以AC2 =AB2+BC2 =42+32= 48.
因为6.922≈47.886, 6.932≈48.025,
所以6.92 cm
【考点】勾股定理
【解析】【分析】要运用两次勾股定理,首先求得底面的对角线,在利用勾股定理即可求解。
20.【答案】 解:设AE=x m时,它到两广场的距离相等,
则BE=(1 700- x)m,
由题意得1 2002+x2=(1 700-x)2+ 5002 ,
解得x=500.
答:这个单车停放点E应建在距点A500 m处,它到两广场的距离相等.
【考点】勾股定理的应用
【解析】【分析】设AE的长度为x,根据其到两个广场的距离相等列出方程,解方程得到答案即可。
21.【答案】 解:(1)OD是等腰三角形的底边时,P就是OD的垂直平分线与CB的交点,此时OP=PD≠5;
(2)OD是等腰三角形的一条腰时:
①若点O是顶角顶点时,P点就是以点O为圆心,以5为半径的弧与CB的交点,
在直角△OPC中,CP= =3,则P的坐标是(3,4);
②若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,
过D作DM⊥BC于点M,
在直角△PDM中,PM= =3,
当P在M的左边时,CP=5-3=2,则P的坐标是(2,4);
当P在M的右侧时,CP=5+3=8,则P的坐标是(8,4).
故P的坐标为:(3,4)或(2,4)或(8,4).
【考点】勾股定理,矩形的性质
【解析】【分析】分类讨论,利用勾股定理进行求解即可。
22.【答案】 解:∵A(0,8),C(20,0),四边形OABC是矩形,D是OC的中点,
∴OA=8,OD=10,∠OAB=∠COA= ,
①当OP=OD=10时,
过点P作PE⊥OC轴于点E,则PE=8.
在Rt△PEO中,由勾股定理得:OE= ,
即P点的坐标是(6,8);
②当DP=OD=10时,
过P作PE⊥OC于E,
则PE=OA=8,
由勾股定理得:DE= ,
OE=10-6=4,
即P点坐标是(4,8);
③当OP=DP=10时,
由勾股定理得:DE=OE= ,
即OD=DE+OE=12≠10,即此时不存在;
④当OD=PD时,
过点P作PE⊥OC轴于点E,则PE=8
在Rt△PED中,由勾股定理得:DE= ,
∴OE=OD+DE=10+6=16
∴此时点P坐标为(16,8).
故P点的坐标为:(6,8)或(4,8)或(16,8).
【考点】等腰三角形的性质,勾股定理,矩形的性质
【解析】【分析】由点A、C的坐标以及矩形的性质可得OA=8,OD=10,∠OAB=∠COA=90°,①当OP=OD=10时,过点P作PE⊥OC轴于点E,则PE=8,在Rt△PEO中,由勾股定理求得OE,据此可得点P的坐标;②当DP=OD=10时,过P作PE⊥OC于E,则PE=OA=8,由勾股定理求出DE,进而得OE,据此可得点P的坐标;③当OP=DP=10时,由勾股定理得:DE=OE=6,求出OD,判断出此种情况不存在;④当OD=PD时,过点P作PE⊥OC轴于点E,则PE=8,在Rt△PED中,由勾股定理求得DE,进而求出OE,据此可得点P的坐标.
23.【答案】 解:如图,连接C'E,
设DE=D'E=x,
∵在矩形ABCD中,AB=6,BC=9,
∴CD=AB=6,AD=BC=9,∠A=∠D=90°,
∴AE=AD-DE=9-x,
∵折叠,
∴∠D'=∠D=90°,C'D'=CD=6,
∵点C'为AB边的中点,
∴AC'= AB=3,
在Rt△AEC'中,C'E2=AE2+AC'2=32+(9-x)2 ,
在Rt△C'D'E中,C'E2=C'D'2+D'E2=62+x2 ,
∴32+(9-x)2=62+x2 ,
解得x=3,
∴线段ED的长为3.
【考点】勾股定理
【解析】【分析】连接C'E,设DE=D'E=x,则AE=9-x,利用两次勾股定理分别表示出C'E2 , 进而得到方程求解即可.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
