苏科版八上第二章 第11课时 勾股定理与平方根单元复习
文档属性
| 名称 | 苏科版八上第二章 第11课时 勾股定理与平方根单元复习 |
|
|
| 格式 | zip | ||
| 文件大小 | 66.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-30 00:00:00 | ||
图片预览


文档简介
第11课时 勾股定理与平方根单元复习
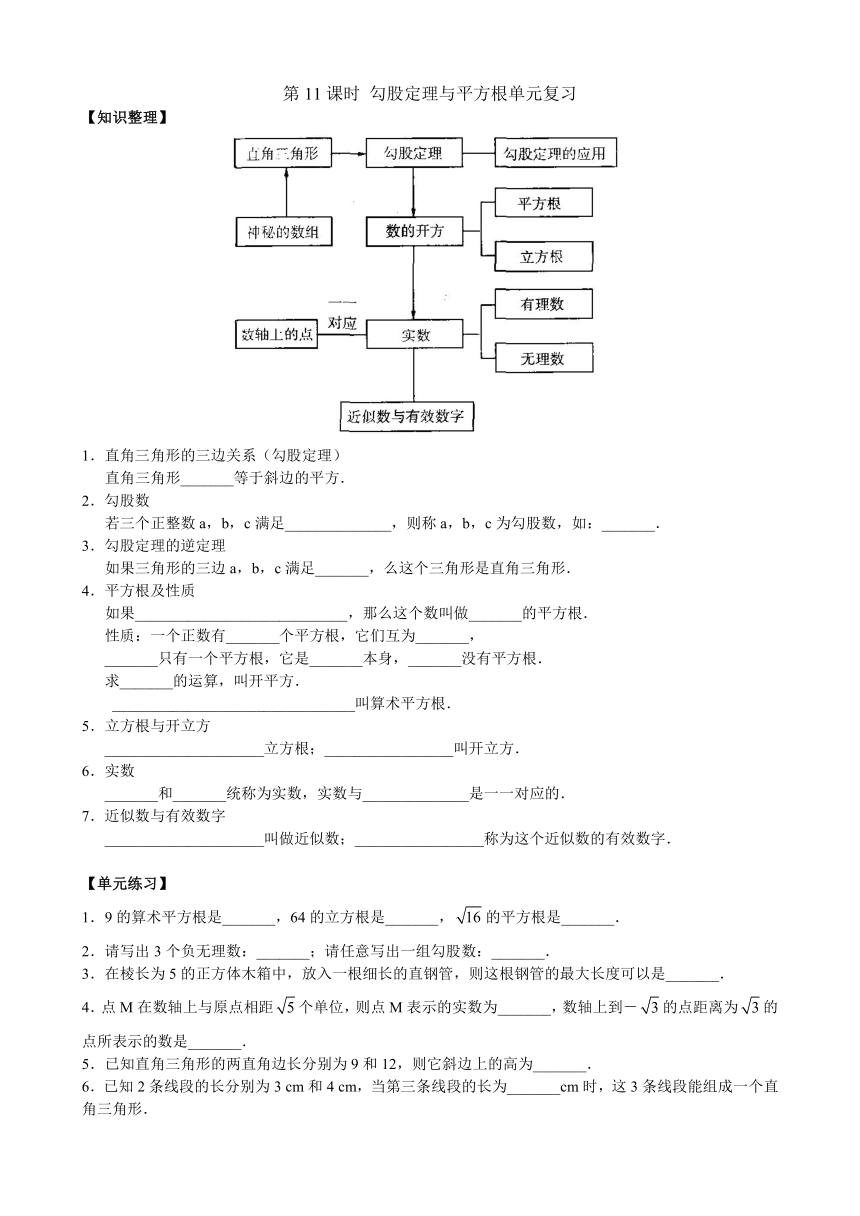
【知识整理】
1.直角三角形的三边关系(勾股定理)
直角三角形_______等于斜边的平方.
2.勾股数
若三个正整数a,b,c满足______________,则称a,b,c为勾股数,如:_______.
3.勾股定理的逆定理
如果三角形的三边a,b,c满足_______,么这个三角形是直角三角形.
4.平方根及性质
如果____________________________,那么这个数叫做_______的平方根.
性质:一个正数有_______个平方根,它们互为_______,
_______只有一个平方根,它是_______本身,_______没有平方根.
求_______的运算,叫开平方.
________________________________叫算术平方根.
5.立方根与开立方
_____________________立方根;_________________叫开立方.
6.实数
_______和_______统称为实数,实数与______________是一一对应的.
7.近似数与有效数字
_____________________叫做近似数;_________________称为这个近似数的有效数字.
【单元练习】
1.9的算术平方根是_______,64的立方根是_______,的平方根是_______.
2.请写出3个负无理数:_______;请任意写出一组勾股数:_______.
3.在棱长为5的正方体木箱中,放入一根细长的直钢管,则这根钢管的最大长度可以是_______.
4.点M在数轴上与原点相距个单位,则点M表示的实数为_______,数轴上到-的点距离为的点所表示的数是_______.
5.已知直角三角形的两直角边长分别为9和12,则它斜边上的高为_______.
6.已知2条线段的长分别为3 cm和4 cm,当第三条线段的长为_______cm时,这3条线段能组成一个直角三角形.
7.如图,在锐角三角形ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点.则BM+MN的最小值是_______.
8.在5,0.1,,,,,这八个实数中,无理数的个数是 ( )
A.5 B.4 C.3 D.2
9.下列运算:①;②;③;④;⑤,其中错误的有 ( )
A.2个 B.3个 C.4个 D.5个
10.下列长度的各组线段中,能够组成直角三角形的是 ( )
A.5,6,7 B.5,11,12 C.7,20,25 D.8,15,17
11.如果梯子的底端离建筑物5m,13 m长的梯子可以达到建筑物的高度是 ( )
A.12 m B.13 m C.14 m D.15 m
12.对于四舍五入得到的近似数2.81×104,下列说法正确的是 ( )
A.有3个有效数字,精确到百位
B.有5个有效数字,精确到个位
C.有2个有效数字,精确到万位
D.有3个有效数字,精确到百分位
13.如图是由4个边长为1的正方形构成的“田字格”,只用没有刻度的直尺在这个“田字格”中最多可以作出长度为的线段有 ( )
A.4条 B.6条 C.8条 D.10条
14.代数式的最小值是 ( )
A.0 B.3 C. D.不存在
15.已知x,y都是实数,且,试求xy的值.
16.已知实数a,b互为相反数,c,d互为倒数,x的绝对值为.求代数式x2+(a+b+cd)x+的值.
17.如图是一块由边长为20 cm的正方形地砖铺设的广场,一只鸽子落在点A处,它想先后吃到小朋友撒在B、C处的鸟食,则鸽子至少需要走多远的路程?
18.如图甲是第七届国际数学教育大会的会徽,会徽的主体图案是由如图乙的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1.如果把图乙中的直角三角形继续作下去,那么OA1,OA2,…OA25这些线段中有多少条线段的长度为正整数?
19.如图,在Rt△ABC中∠C=90°,D、E分别为BC、AC的中点,AD=5,BE=2,求AB的长.
20.学校科技小组研制了一套信号发射、接收系统,在对系统进行测试中,如图,小明从路口A处出发,沿东南方向笔直公路行进,并发射信号,小华同时从A处出发,沿西南方向笔直公路行进,并接收信号,若小明的步行速度为39 m/min,小华的步行速度为52 m/min,恰好在出发后30 min时信号开始不清晰.
(1)你能求出他们研制的信号收发系统的信号传送半径吗?(以信号清晰为界限)
(2)通过计算,你能找到题中数据与勾股数3,4,5的联系吗?试从中寻找求解决问题的简便算法.
21.勾股定理有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了两枚以勾股图为背景的邮票,所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR使得∠R=90°,点H在边QR上,点D、E在边PR上,点G、F在边PQ上,求△PQR的周长.
22.有一块直角三角形的绿地,量得两直角边长分别为6m,8m现在要将绿地扩充成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.
参考答案
1.3 4 ±2 2.略 3.5 4.± 0或-2 5.7 2 6.或5 7.4
8.C 9.C 10.D 11.A 12.A 13.C 14.B
15.8 16.7± 17.18 cm 18.5条 19.2
20.(1)1950m (2) 1950m 21.27+13
22.三种情况:(1)如图①32m.(2)如图②(20+4)m.(3)如图③
【知识整理】
1.直角三角形的三边关系(勾股定理)
直角三角形_______等于斜边的平方.
2.勾股数
若三个正整数a,b,c满足______________,则称a,b,c为勾股数,如:_______.
3.勾股定理的逆定理
如果三角形的三边a,b,c满足_______,么这个三角形是直角三角形.
4.平方根及性质
如果____________________________,那么这个数叫做_______的平方根.
性质:一个正数有_______个平方根,它们互为_______,
_______只有一个平方根,它是_______本身,_______没有平方根.
求_______的运算,叫开平方.
________________________________叫算术平方根.
5.立方根与开立方
_____________________立方根;_________________叫开立方.
6.实数
_______和_______统称为实数,实数与______________是一一对应的.
7.近似数与有效数字
_____________________叫做近似数;_________________称为这个近似数的有效数字.
【单元练习】
1.9的算术平方根是_______,64的立方根是_______,的平方根是_______.
2.请写出3个负无理数:_______;请任意写出一组勾股数:_______.
3.在棱长为5的正方体木箱中,放入一根细长的直钢管,则这根钢管的最大长度可以是_______.
4.点M在数轴上与原点相距个单位,则点M表示的实数为_______,数轴上到-的点距离为的点所表示的数是_______.
5.已知直角三角形的两直角边长分别为9和12,则它斜边上的高为_______.
6.已知2条线段的长分别为3 cm和4 cm,当第三条线段的长为_______cm时,这3条线段能组成一个直角三角形.
7.如图,在锐角三角形ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点.则BM+MN的最小值是_______.
8.在5,0.1,,,,,这八个实数中,无理数的个数是 ( )
A.5 B.4 C.3 D.2
9.下列运算:①;②;③;④;⑤,其中错误的有 ( )
A.2个 B.3个 C.4个 D.5个
10.下列长度的各组线段中,能够组成直角三角形的是 ( )
A.5,6,7 B.5,11,12 C.7,20,25 D.8,15,17
11.如果梯子的底端离建筑物5m,13 m长的梯子可以达到建筑物的高度是 ( )
A.12 m B.13 m C.14 m D.15 m
12.对于四舍五入得到的近似数2.81×104,下列说法正确的是 ( )
A.有3个有效数字,精确到百位
B.有5个有效数字,精确到个位
C.有2个有效数字,精确到万位
D.有3个有效数字,精确到百分位
13.如图是由4个边长为1的正方形构成的“田字格”,只用没有刻度的直尺在这个“田字格”中最多可以作出长度为的线段有 ( )
A.4条 B.6条 C.8条 D.10条
14.代数式的最小值是 ( )
A.0 B.3 C. D.不存在
15.已知x,y都是实数,且,试求xy的值.
16.已知实数a,b互为相反数,c,d互为倒数,x的绝对值为.求代数式x2+(a+b+cd)x+的值.
17.如图是一块由边长为20 cm的正方形地砖铺设的广场,一只鸽子落在点A处,它想先后吃到小朋友撒在B、C处的鸟食,则鸽子至少需要走多远的路程?
18.如图甲是第七届国际数学教育大会的会徽,会徽的主体图案是由如图乙的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1.如果把图乙中的直角三角形继续作下去,那么OA1,OA2,…OA25这些线段中有多少条线段的长度为正整数?
19.如图,在Rt△ABC中∠C=90°,D、E分别为BC、AC的中点,AD=5,BE=2,求AB的长.
20.学校科技小组研制了一套信号发射、接收系统,在对系统进行测试中,如图,小明从路口A处出发,沿东南方向笔直公路行进,并发射信号,小华同时从A处出发,沿西南方向笔直公路行进,并接收信号,若小明的步行速度为39 m/min,小华的步行速度为52 m/min,恰好在出发后30 min时信号开始不清晰.
(1)你能求出他们研制的信号收发系统的信号传送半径吗?(以信号清晰为界限)
(2)通过计算,你能找到题中数据与勾股数3,4,5的联系吗?试从中寻找求解决问题的简便算法.
21.勾股定理有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了两枚以勾股图为背景的邮票,所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR使得∠R=90°,点H在边QR上,点D、E在边PR上,点G、F在边PQ上,求△PQR的周长.
22.有一块直角三角形的绿地,量得两直角边长分别为6m,8m现在要将绿地扩充成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.
参考答案
1.3 4 ±2 2.略 3.5 4.± 0或-2 5.7 2 6.或5 7.4
8.C 9.C 10.D 11.A 12.A 13.C 14.B
15.8 16.7± 17.18 cm 18.5条 19.2
20.(1)1950m (2) 1950m 21.27+13
22.三种情况:(1)如图①32m.(2)如图②(20+4)m.(3)如图③
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
