苏科版八上第二章 第9课时 勾股定理的应用(1) 课时训练
文档属性
| 名称 | 苏科版八上第二章 第9课时 勾股定理的应用(1) 课时训练 | 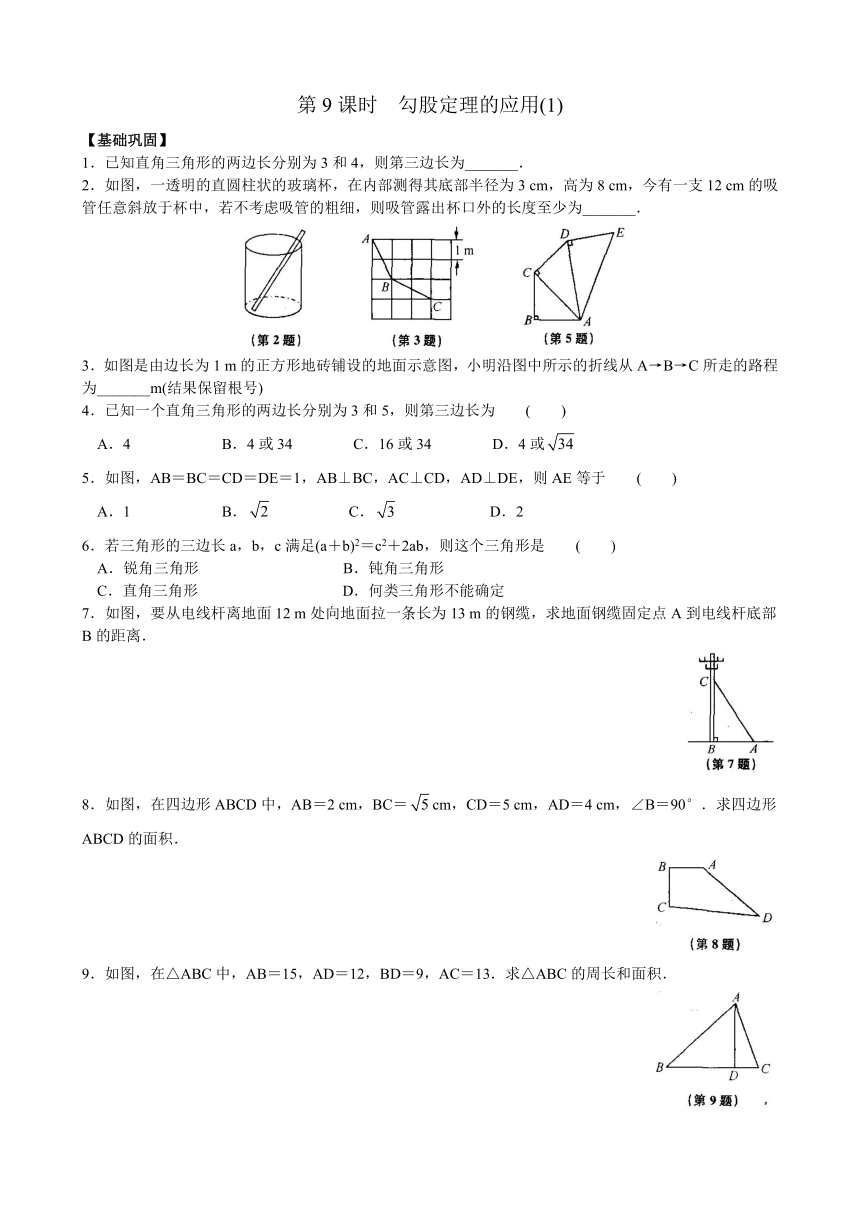 | |
| 格式 | zip | ||
| 文件大小 | 33.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-30 08:58:19 | ||
图片预览

文档简介
第9课时 勾股定理的应用(1)
【基础巩固】
1.已知直角三角形的两边长分别为3和4,则第三边长为_______.
2.如图,一透明的直圆柱状的玻璃杯,在内部测得其底部半径为3 cm,高为8 cm,今有一支12 cm的吸管任意斜放于杯中,若不考虑吸管的粗细,则吸管露出杯口外的长度至少为_______.
3.如图是由边长为1 m的正方形地砖铺设的地面示意图,小明沿图中所示的折线从A→B→C所走的路程为_______m(结果保留根号)
4.已知一个直角三角形的两边长分别为3和5,则第三边长为 ( )
A.4 B.4或34 C.16或34 D.4或
5.如图,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则AE等于 ( )
A.1 B. C. D.2
6.若三角形的三边长a,b,c满足(a+b)2=c2+2ab,则这个三角形是 ( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.何类三角形不能确定
7.如图,要从电线杆离地面12 m处向地面拉一条长为13 m的钢缆,求地面钢缆固定点A到电线杆底部B的距离.
8.如图,在四边形ABCD中,AB=2 cm,BC=cm,CD=5 cm,AD=4 cm,∠B=90°.求四边形ABCD的面积.
9.如图,在△ABC中,AB=15,AD=12,BD=9,AC=13.求△ABC的周长和面积.
10.如图,某菜农要修建一个育苗棚,棚宽a=12 m,高b=5 m,长d=20 m,请你帮他算一下覆盖在顶上的塑料薄膜的面积.
【拓展提优】
11.已知a,b,c为三个正整数,如果a+b+c=12,那么以a,b,c为边能组成的三角形是:①等腰三角形;②等边三角形;③直角三角形;④钝角三角形,以上符合条件的正确结论是_______.(只填序号)
12.如图,3×3网格中一个四边形ABCD,若小方格正方形的边长为1,则四边形ABCD的周长_______.
13.一架2.5 m长的梯子斜靠在一竖直的墙上,这时梯脚距离墙角0.7 m,如果梯子的顶端沿墙下滑0.4 m,那么梯脚移动的距离是 ( )
A.1.5 m B.0.9 m C.0.8 m D.0.5m
14.如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是 ( )
A.5 B.25 C.10+5 D.35
15.一张长方形纸片宽AB=8 cm,长BC=10 cm现将纸片折叠,使顶点D落在BC边上的点F处(折痕为AE),求EC的长.
16.如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5 cm,求AB的长.
17.[问题情境]
勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
[定理表述]
请你根据图①中的直角三角形叙述勾股定理(用文字及符号语言叙述);
[尝试证明]
以图①中的直角三角形为基础,可以构造出以a,b为底,以a+b为高的直角梯形(如图②),请你利用图②,验证勾股定理;
[知识拓展]
利用图②中的直角梯形,我们可以证明<.其证明步骤如下:
因为BC=a+b,AD=_______,
又因为在直角梯形ABCD中,有BC_______AD(填大小关系),即_______.
参考答案
【基础巩固】
1.5 2.2 3.2 4.D 5.D 6.C 7.5m 8.(6+)cm2
9.周长:42 面积:84 10.260m2
【拓展提优】
11.①②③ 12.3+2 13.C 14.B 15.3 cm 16.10 cm
17.[定理表述]如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
[尝试证明]略
[知识拓展]c <
【基础巩固】
1.已知直角三角形的两边长分别为3和4,则第三边长为_______.
2.如图,一透明的直圆柱状的玻璃杯,在内部测得其底部半径为3 cm,高为8 cm,今有一支12 cm的吸管任意斜放于杯中,若不考虑吸管的粗细,则吸管露出杯口外的长度至少为_______.
3.如图是由边长为1 m的正方形地砖铺设的地面示意图,小明沿图中所示的折线从A→B→C所走的路程为_______m(结果保留根号)
4.已知一个直角三角形的两边长分别为3和5,则第三边长为 ( )
A.4 B.4或34 C.16或34 D.4或
5.如图,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则AE等于 ( )
A.1 B. C. D.2
6.若三角形的三边长a,b,c满足(a+b)2=c2+2ab,则这个三角形是 ( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.何类三角形不能确定
7.如图,要从电线杆离地面12 m处向地面拉一条长为13 m的钢缆,求地面钢缆固定点A到电线杆底部B的距离.
8.如图,在四边形ABCD中,AB=2 cm,BC=cm,CD=5 cm,AD=4 cm,∠B=90°.求四边形ABCD的面积.
9.如图,在△ABC中,AB=15,AD=12,BD=9,AC=13.求△ABC的周长和面积.
10.如图,某菜农要修建一个育苗棚,棚宽a=12 m,高b=5 m,长d=20 m,请你帮他算一下覆盖在顶上的塑料薄膜的面积.
【拓展提优】
11.已知a,b,c为三个正整数,如果a+b+c=12,那么以a,b,c为边能组成的三角形是:①等腰三角形;②等边三角形;③直角三角形;④钝角三角形,以上符合条件的正确结论是_______.(只填序号)
12.如图,3×3网格中一个四边形ABCD,若小方格正方形的边长为1,则四边形ABCD的周长_______.
13.一架2.5 m长的梯子斜靠在一竖直的墙上,这时梯脚距离墙角0.7 m,如果梯子的顶端沿墙下滑0.4 m,那么梯脚移动的距离是 ( )
A.1.5 m B.0.9 m C.0.8 m D.0.5m
14.如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是 ( )
A.5 B.25 C.10+5 D.35
15.一张长方形纸片宽AB=8 cm,长BC=10 cm现将纸片折叠,使顶点D落在BC边上的点F处(折痕为AE),求EC的长.
16.如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5 cm,求AB的长.
17.[问题情境]
勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
[定理表述]
请你根据图①中的直角三角形叙述勾股定理(用文字及符号语言叙述);
[尝试证明]
以图①中的直角三角形为基础,可以构造出以a,b为底,以a+b为高的直角梯形(如图②),请你利用图②,验证勾股定理;
[知识拓展]
利用图②中的直角梯形,我们可以证明<.其证明步骤如下:
因为BC=a+b,AD=_______,
又因为在直角梯形ABCD中,有BC_______AD(填大小关系),即_______.
参考答案
【基础巩固】
1.5 2.2 3.2 4.D 5.D 6.C 7.5m 8.(6+)cm2
9.周长:42 面积:84 10.260m2
【拓展提优】
11.①②③ 12.3+2 13.C 14.B 15.3 cm 16.10 cm
17.[定理表述]如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
[尝试证明]略
[知识拓展]c <
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
