新人教版九年级上册24.2.2.3切线长定理
文档属性
| 名称 | 新人教版九年级上册24.2.2.3切线长定理 |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-30 09:04:09 | ||
图片预览

文档简介
(共27张PPT)
新课学习
P
A
O
B
1、如何过⊙O外一点P画出⊙O的切线?
2、这样的切线能画出几条?
如下左图,借助三角板,我们可以画出PA是⊙O的切线。
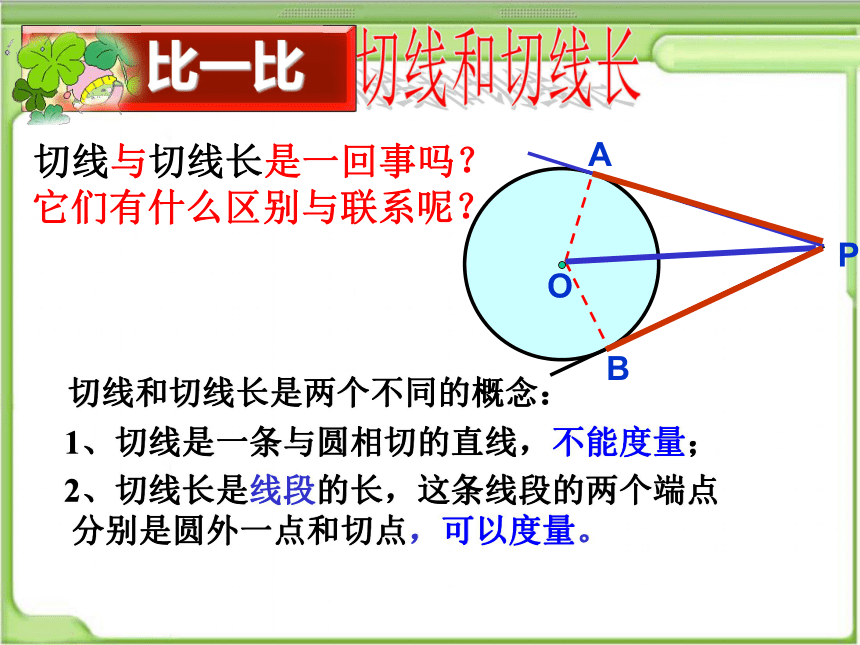
画一画
在经过圆外一点做圆的切线,这一点和切点之间的线段的长叫做这点到圆的切线长
F
A
P
B
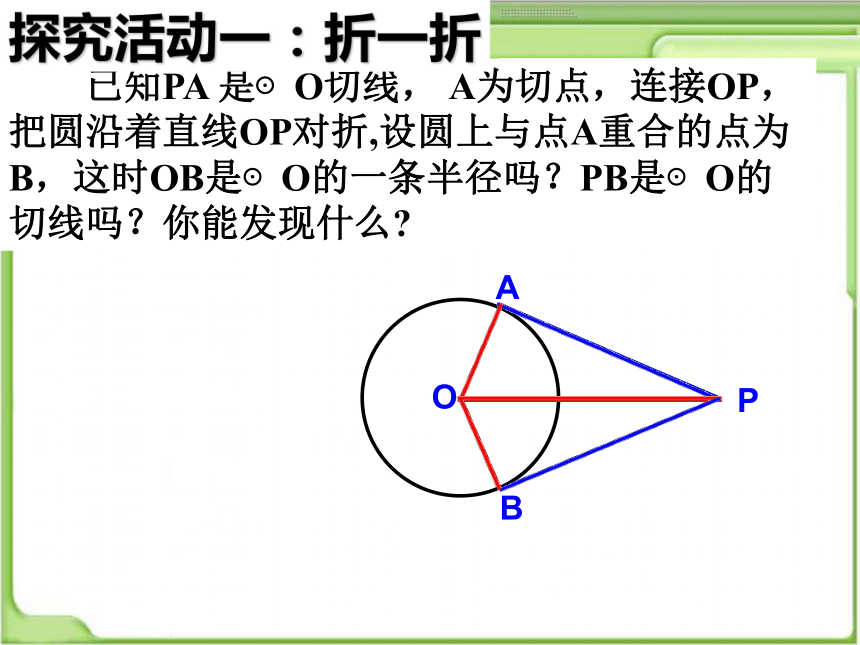
切线和切线长是两个不同的概念:
1、切线是一条与圆相切的直线,不能度量;
2、切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。
比一比
切线与切线长是一回事吗?
它们有什么区别与联系呢?
B
P
O
A
已知PA 是⊙O切线, A为切点,连接OP,把圆沿着直线OP对折,设圆上与点A重合的点为B,这时OB是⊙O的一条半径吗?PB是⊙O的切线吗?你能发现什么
探究活动一:折一折
P
A
O
B
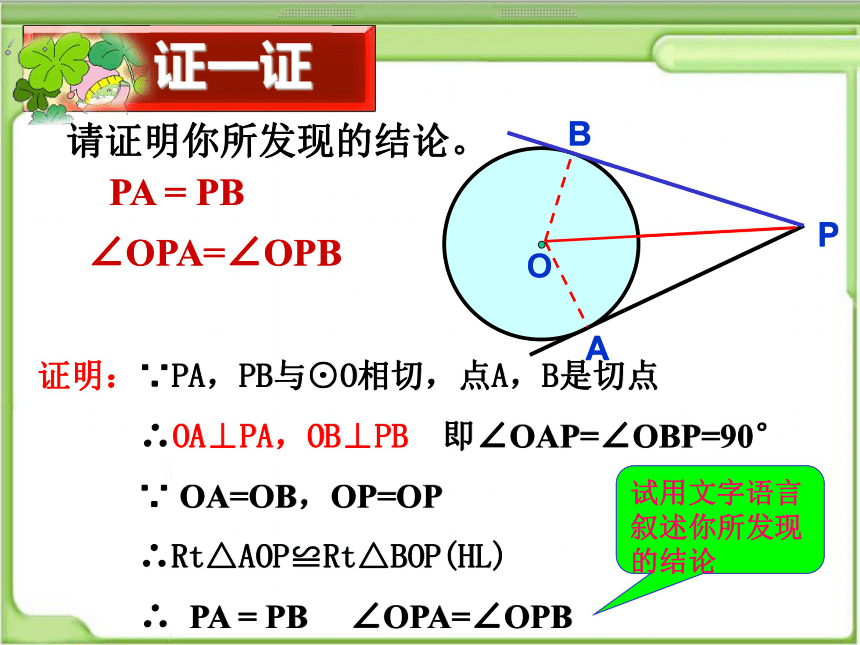
请证明你所发现的结论。
A
P
O
B
PA = PB
∠OPA=∠OPB
证明:∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB ∠OPA=∠OPB
试用文字语言叙述你所发现的结论
证一证
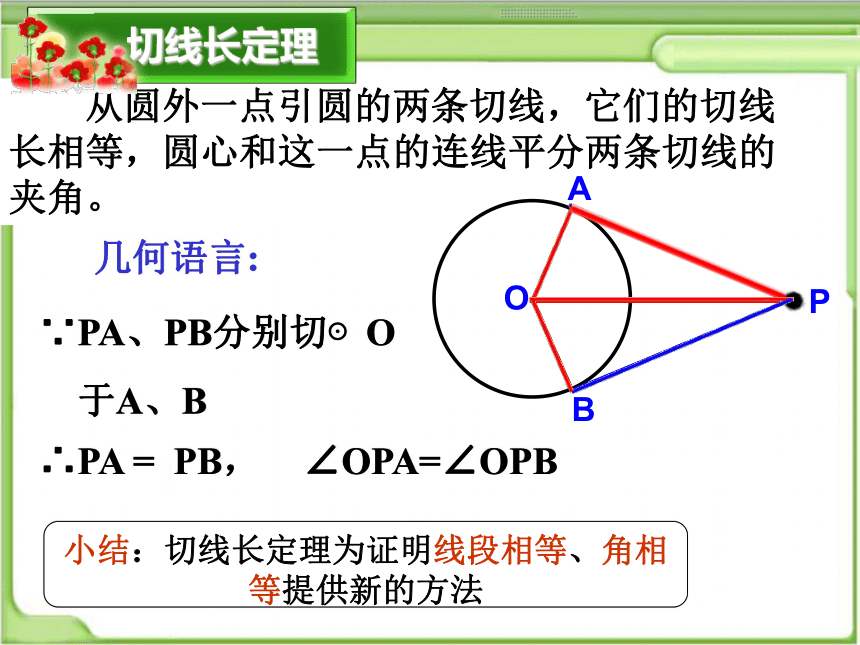
∵PA、PB分别切⊙O
于A、B
∴PA = PB,
∠OPA=∠OPB
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
几何语言:
小结:切线长定理为证明线段相等、角相等提供新的方法
切线长定理
P
A
O
B
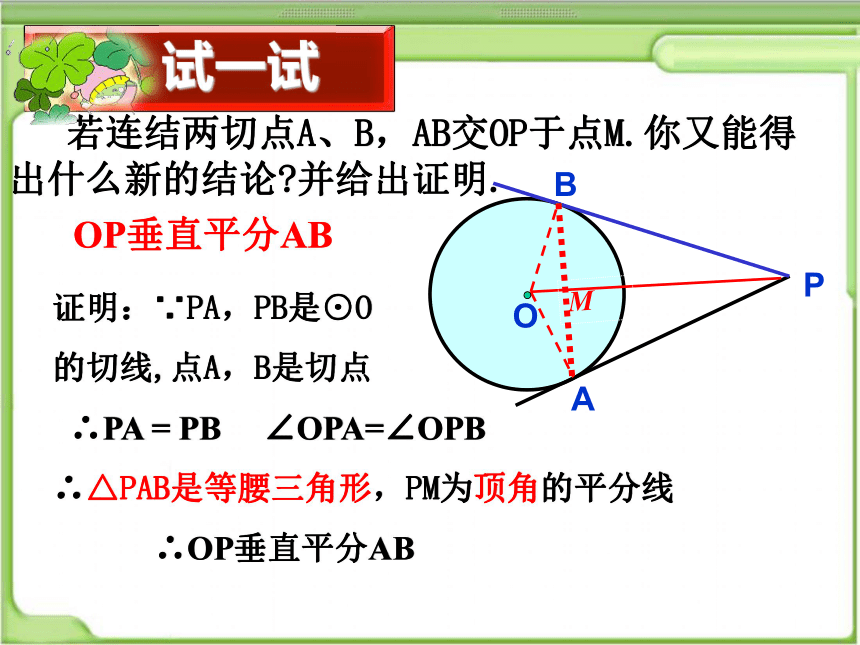
若连结两切点A、B,AB交OP于点M.你又能得出什么新的结论 并给出证明.
OP垂直平分AB
证明:∵PA,PB是⊙O
的切线,点A,B是切点
∴PA = PB ∠OPA=∠OPB
∴△PAB是等腰三角形,PM为顶角的平分线
∴OP垂直平分AB
试一试
A
P
O
B
M
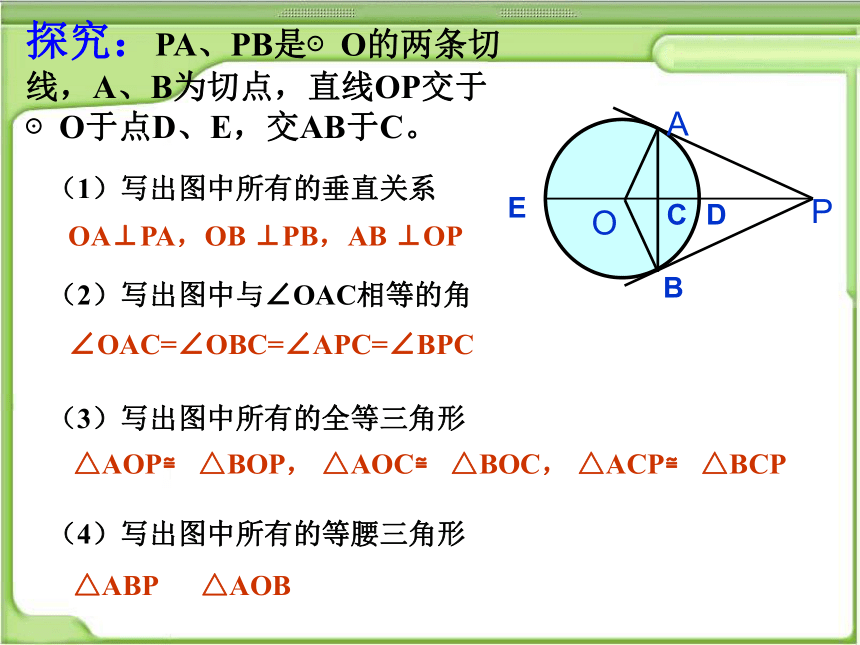
探究:PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。
B
A
P
O
C
E
D
(1)写出图中所有的垂直关系
OA⊥PA,OB ⊥PB,AB ⊥OP
(3)写出图中所有的全等三角形
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP
(4)写出图中所有的等腰三角形
△ABP △AOB
(2)写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC
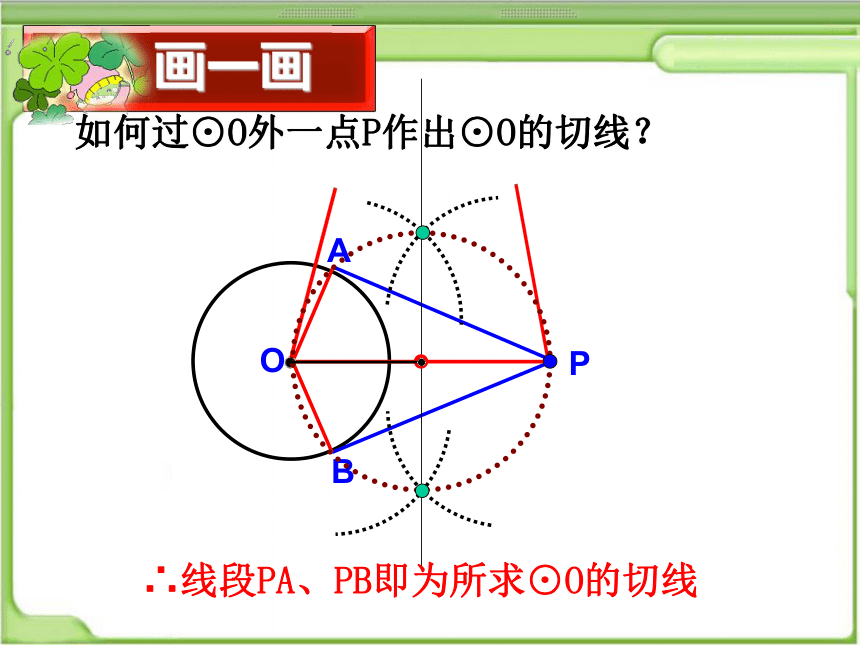
如何过⊙O外一点P作出⊙O的切线?
画一画
P
A
O
B
∴线段PA、PB即为所求⊙O的切线
(2)已知OA=3cm,OP=6cm,则∠APB=
P
A
B
C
O
60°
(4)OP交⊙O于M,则 ,AB OP
AM=BM
⌒
⌒
M
⊥
牛刀小试
(3)若∠APB=70°,则∠AOB= °
110
(1)若PA=4、PM=2,求圆O的半径OA
OA=3
例1、已知:P为⊙O外一点,PA、PB为⊙O的
切线,A、B为切点,BC是直径。
求证:AC∥OP
P
A
C
B
D
O
例题讲解
。
P
B
A
O
(3)连结圆心和圆外一点
(2)连结两切点
(1)分别连结圆心和切点
反思:在解决有关圆的切线长问题时,往往需要我们构建基本图形。
想一想
已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点。
E
A
Q
P
F
B
O
EQ=EA, FQ=FB,PA=PB
∴ PE+EQ=PA=12cm
PF+FQ=PB=PA=12cm
∴周长为24cm
牛刀再试
1.找出图中所有相等的切线长
2.已知PA=12CM,求△PEF的周长。
例3 、如图,四边形ABCD的边AB、BC、CD、DA和圆⊙O分别相切于点L、M、N、P,
求证: AD+BC=AB+CD
D
L
M
N
A
B
C
O
P
证明:由切线长定理得
∴AL=AP=aLB=MB=b,
NC=MC=c,DN=DP=d
∴AL+LB+NC+DN=a+b+c+d
即 AB+CD=AD+BC
补充:圆的外切四边形的两组对边的和相等.
a
a
b
b
c
c
d
d
AP+MB+MC+DP=a+b+c+d
如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
A
B
C
三角形的内切圆
A
B
C
探究活动二:
1、定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。
O
A
B
C
作三角形内切圆的方法:
A
B
C
1、作∠B、∠C的平分线BM和CN,交点为I。
I
2.过点I作ID⊥BC,垂足为D。
3.以I为圆心,ID为半径作⊙I.
⊙I就是所求的圆。
D
M
N
作三角形内切圆的方法:
A
B
C
E
G
H
D
F
M
∴ ⊙I即为所求的⊿ABC的圆
性质: 三角形的内心是三角形内切圆的圆心,它到三角形三边的距离相等;内心与顶点连线平分内角。任何三角形的内心都在三角形的内部
练习1.(口答)如图所示PA、PB分别切
圆O于A、B,并与圆O的切线分别相交于
C、D,已知PA=7cm,
(1)求△PCD的周长.
(2) 如果∠P=46°,求∠COD的度数
C
· O
P
B
D
A
E
(1)∵点O是△ABC的内心,
∴ ∠BOC=180 °-(∠1+ ∠3)
= 180 °-(25°+ 35 °)
例2 如图,在△ABC中,点O是内心, 若∠ABC=50°, ∠ACB=70°,求∠BOC的度数
A
B
C
O
=120 °
)
1
(
3
2
)
4
(
同理 ∠3= ∠4= ∠ACB= 70° = 35°
∴ ∠1= ∠2= ∠ABC= 50°= 25°
例1:已知:在△ABC中,BC=9cm,AC=14cm,AB=13cm,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长。
C
B
A
E
D
F
O
r
解:因为△ABC的内切圆分别和BC、AC、AB切于点D、E、F,由切线长定理知
AE=AF,CE=CD,BD=BF
14
13
9
设AE=AF=x,则CE=CD=14-x,BD=BF=13-x
∴(14-x)+(13-x)=9
∴x=9
∴AE=AF=9,CE=CD=5,BD=BF=4
1、若直角三角形的两直角边分别
为6,8,则该直角三角形的外接
圆半径为 。
2、若直角三角形的两直角边分别
为5,12,则该直角三角形的内切
圆半径为 。
3、若Rt△的周长为24,面积为48,
则该Rt△的内切圆半径为 。
例.如图,△ABC中,∠C =90 ,它的
内切圆O分别与边AB、BC、CA相切
于点D、E、F,且BD=12,AD=8,
求⊙O的半径r.
O
E
B
D
C
A
F
练习2.如图,AB是⊙O的直径,AD、DC、BC是切线,点A、E、B为切点,
(1)求证:OD ⊥ OC
(2)若BC=9,AD=4,求OB的长.
O
A
B
C
D
E
· O
A
B
C
D
E
F
O
A
B
C
D
E
选做题:如图,AB是⊙O的直径,
AD、DC、BC是切线,点A、E、B
为切点,若BC=9,AD=4,求OE的长.
新课学习
P
A
O
B
1、如何过⊙O外一点P画出⊙O的切线?
2、这样的切线能画出几条?
如下左图,借助三角板,我们可以画出PA是⊙O的切线。
画一画
在经过圆外一点做圆的切线,这一点和切点之间的线段的长叫做这点到圆的切线长
F
A
P
B
切线和切线长是两个不同的概念:
1、切线是一条与圆相切的直线,不能度量;
2、切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。
比一比
切线与切线长是一回事吗?
它们有什么区别与联系呢?
B
P
O
A
已知PA 是⊙O切线, A为切点,连接OP,把圆沿着直线OP对折,设圆上与点A重合的点为B,这时OB是⊙O的一条半径吗?PB是⊙O的切线吗?你能发现什么
探究活动一:折一折
P
A
O
B
请证明你所发现的结论。
A
P
O
B
PA = PB
∠OPA=∠OPB
证明:∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB ∠OPA=∠OPB
试用文字语言叙述你所发现的结论
证一证
∵PA、PB分别切⊙O
于A、B
∴PA = PB,
∠OPA=∠OPB
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
几何语言:
小结:切线长定理为证明线段相等、角相等提供新的方法
切线长定理
P
A
O
B
若连结两切点A、B,AB交OP于点M.你又能得出什么新的结论 并给出证明.
OP垂直平分AB
证明:∵PA,PB是⊙O
的切线,点A,B是切点
∴PA = PB ∠OPA=∠OPB
∴△PAB是等腰三角形,PM为顶角的平分线
∴OP垂直平分AB
试一试
A
P
O
B
M
探究:PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。
B
A
P
O
C
E
D
(1)写出图中所有的垂直关系
OA⊥PA,OB ⊥PB,AB ⊥OP
(3)写出图中所有的全等三角形
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP
(4)写出图中所有的等腰三角形
△ABP △AOB
(2)写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC
如何过⊙O外一点P作出⊙O的切线?
画一画
P
A
O
B
∴线段PA、PB即为所求⊙O的切线
(2)已知OA=3cm,OP=6cm,则∠APB=
P
A
B
C
O
60°
(4)OP交⊙O于M,则 ,AB OP
AM=BM
⌒
⌒
M
⊥
牛刀小试
(3)若∠APB=70°,则∠AOB= °
110
(1)若PA=4、PM=2,求圆O的半径OA
OA=3
例1、已知:P为⊙O外一点,PA、PB为⊙O的
切线,A、B为切点,BC是直径。
求证:AC∥OP
P
A
C
B
D
O
例题讲解
。
P
B
A
O
(3)连结圆心和圆外一点
(2)连结两切点
(1)分别连结圆心和切点
反思:在解决有关圆的切线长问题时,往往需要我们构建基本图形。
想一想
已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点。
E
A
Q
P
F
B
O
EQ=EA, FQ=FB,PA=PB
∴ PE+EQ=PA=12cm
PF+FQ=PB=PA=12cm
∴周长为24cm
牛刀再试
1.找出图中所有相等的切线长
2.已知PA=12CM,求△PEF的周长。
例3 、如图,四边形ABCD的边AB、BC、CD、DA和圆⊙O分别相切于点L、M、N、P,
求证: AD+BC=AB+CD
D
L
M
N
A
B
C
O
P
证明:由切线长定理得
∴AL=AP=aLB=MB=b,
NC=MC=c,DN=DP=d
∴AL+LB+NC+DN=a+b+c+d
即 AB+CD=AD+BC
补充:圆的外切四边形的两组对边的和相等.
a
a
b
b
c
c
d
d
AP+MB+MC+DP=a+b+c+d
如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
A
B
C
三角形的内切圆
A
B
C
探究活动二:
1、定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。
O
A
B
C
作三角形内切圆的方法:
A
B
C
1、作∠B、∠C的平分线BM和CN,交点为I。
I
2.过点I作ID⊥BC,垂足为D。
3.以I为圆心,ID为半径作⊙I.
⊙I就是所求的圆。
D
M
N
作三角形内切圆的方法:
A
B
C
E
G
H
D
F
M
∴ ⊙I即为所求的⊿ABC的圆
性质: 三角形的内心是三角形内切圆的圆心,它到三角形三边的距离相等;内心与顶点连线平分内角。任何三角形的内心都在三角形的内部
练习1.(口答)如图所示PA、PB分别切
圆O于A、B,并与圆O的切线分别相交于
C、D,已知PA=7cm,
(1)求△PCD的周长.
(2) 如果∠P=46°,求∠COD的度数
C
· O
P
B
D
A
E
(1)∵点O是△ABC的内心,
∴ ∠BOC=180 °-(∠1+ ∠3)
= 180 °-(25°+ 35 °)
例2 如图,在△ABC中,点O是内心, 若∠ABC=50°, ∠ACB=70°,求∠BOC的度数
A
B
C
O
=120 °
)
1
(
3
2
)
4
(
同理 ∠3= ∠4= ∠ACB= 70° = 35°
∴ ∠1= ∠2= ∠ABC= 50°= 25°
例1:已知:在△ABC中,BC=9cm,AC=14cm,AB=13cm,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长。
C
B
A
E
D
F
O
r
解:因为△ABC的内切圆分别和BC、AC、AB切于点D、E、F,由切线长定理知
AE=AF,CE=CD,BD=BF
14
13
9
设AE=AF=x,则CE=CD=14-x,BD=BF=13-x
∴(14-x)+(13-x)=9
∴x=9
∴AE=AF=9,CE=CD=5,BD=BF=4
1、若直角三角形的两直角边分别
为6,8,则该直角三角形的外接
圆半径为 。
2、若直角三角形的两直角边分别
为5,12,则该直角三角形的内切
圆半径为 。
3、若Rt△的周长为24,面积为48,
则该Rt△的内切圆半径为 。
例.如图,△ABC中,∠C =90 ,它的
内切圆O分别与边AB、BC、CA相切
于点D、E、F,且BD=12,AD=8,
求⊙O的半径r.
O
E
B
D
C
A
F
练习2.如图,AB是⊙O的直径,AD、DC、BC是切线,点A、E、B为切点,
(1)求证:OD ⊥ OC
(2)若BC=9,AD=4,求OB的长.
O
A
B
C
D
E
· O
A
B
C
D
E
F
O
A
B
C
D
E
选做题:如图,AB是⊙O的直径,
AD、DC、BC是切线,点A、E、B
为切点,若BC=9,AD=4,求OE的长.
同课章节目录
