y=ax2+c的图像和性质(1)
图片预览



文档简介
(共15张PPT)
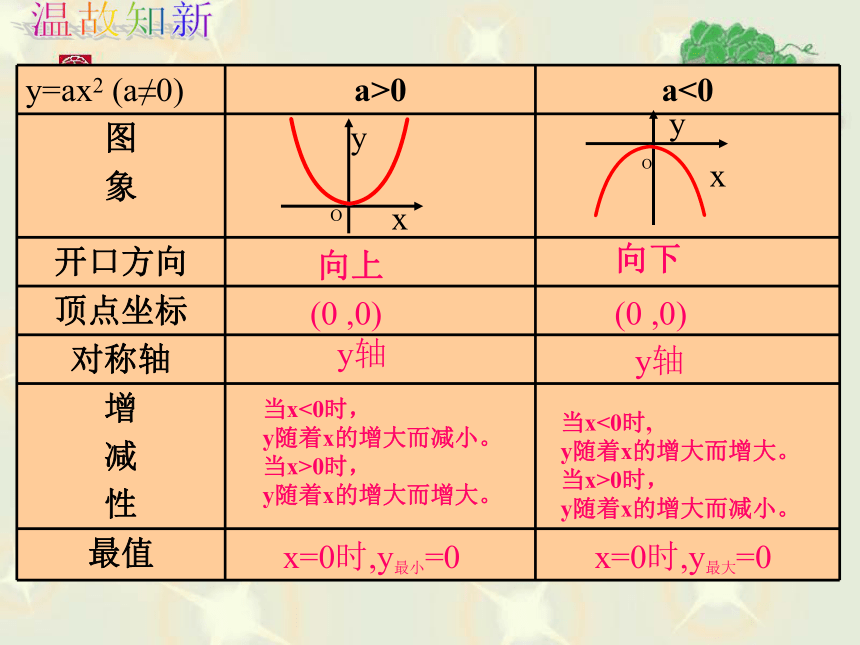
y=ax2 (a≠0) a>0 a<0
图
象
开口方向
顶点坐标
对称轴
增
减
性
最值
x
y
O
y
x
O
向上
向下
(0 ,0)
(0 ,0)
y轴
y轴
当x<0时,
y随着x的增大而减小。
当x>0时,
y随着x的增大而增大。
当x<0时,
y随着x的增大而增大。
当x>0时,
y随着x的增大而减小。
x=0时,y最小=0
x=0时,y最大=0
一位篮球运动员跳起投篮,球沿抛物线 y=一 x2+3.5
运行,然后准确落入蓝筐内,已知蓝筐的中心离地面的
距离为3.05m。
1、球在空中运行的最大高度是多少米?
2、如果运动员跳投时,球出手离地面的高度 为2.25m ,
则他离篮筐中心的水平距离AB是多少?
y=ax2+c的图像和性质(1)
学习目标
1、会画y=ax2+c的图像。
2、掌握y=ax2+c的性质,并能应用性质熟练解决问题。
3、体会数学由特殊到一般、数形结合的思想。
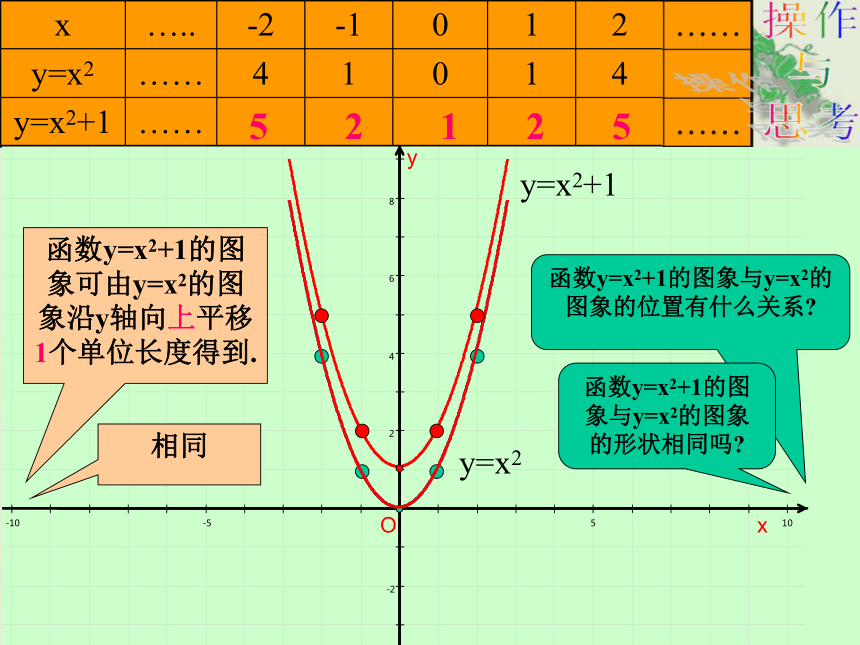
x ….. -2 -1 0 1 2 ……
y=x2 …… 4 1 0 1 4
y=x2+1 …… ……
y=x2
y=x2+1
5 2 1 2 5
函数y=x2+1的图象与y=x2的图象的位置有什么关系
函数y=x2+1的图象可由y=x2的图象沿y轴向上平移1个单位长度得到.
函数y=x2+1的图象与y=x2的图象的形状相同吗
相同
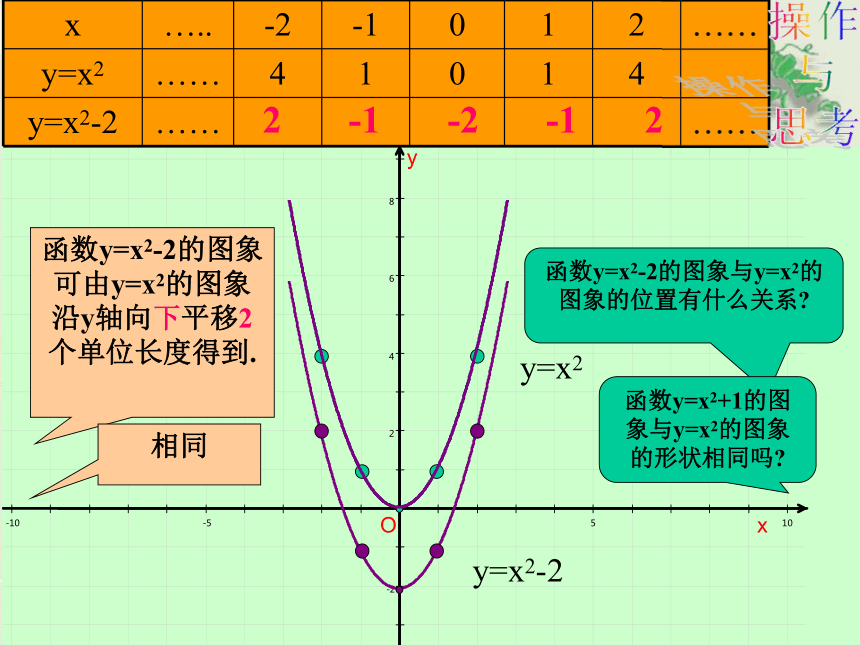
x ….. -2 -1 0 1 2 ……
y=x2 …… 4 1 0 1 4
y=x2-2 …… ……
y=x2
y=x2-2
2 -1 -2 -1 2
函数y=x2-2的图象可由y=x2的图象沿y轴向下平移2个单位长度得到.
函数y=x2-2的图象与y=x2的图象的位置有什么关系
函数y=x2+1的图象与y=x2的图象的形状相同吗
相同
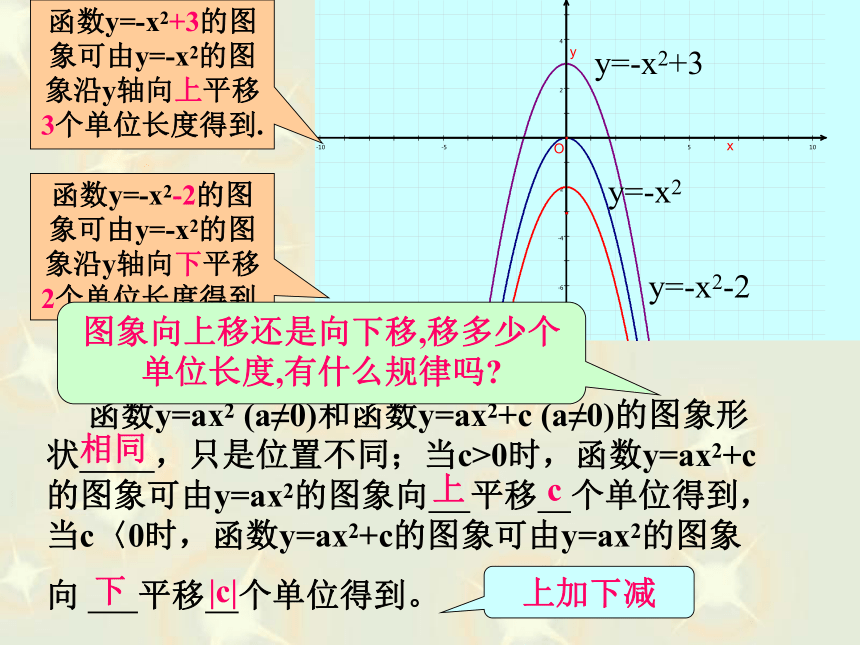
函数y=ax2 (a≠0)和函数y=ax2+c (a≠0)的图象形状 ,只是位置不同;当c>0时,函数y=ax2+c的图象可由y=ax2的图象向 平移 个单位得到,当c〈0时,函数y=ax2+c的图象可由y=ax2的图象
向 平移 个单位得到。
y=-x2-2
y=-x2+3
y=-x2
函数y=-x2-2的图象可由y=-x2的图象沿y轴向下平移2个单位长度得到.
函数y=-x2+3的图象可由y=-x2的图象沿y轴向上平移3个单位长度得到.
图象向上移还是向下移,移多少个单位长度,有什么规律吗
上加下减
相同
上
c
下
|c|
(1)函数y=4x2+5的图象可由y=4x2的图象
向 平移 个单位得到;y=4x2-11的图象
可由 y=4x2的图象向 平移 个单位得到。
(3)将抛物线y=4x2向上平移3个单位,所得的
抛物线的函数式是 。
将抛物线y=-5x2+1向下平移5个单位,所得的
抛物线的函数式是 。
(2)将函数y=-3x2+4的图象向 平移 个单位可得
y=-3x2的图象;将y=2x2-7的图象向 平移 个
单位得到可由 y=2x2的图象。将y=x2-7的图象
向 平移 个单位可得到 y=x2+2的图象。
上
5
下
11
下
4
上
7
上
9
y=4x2+3
y=-5x2-4
当a>0时,抛物线y=ax2+c的开口 ,对称轴是 ,顶点坐标是 ,当x <0时,y随x的增大而 ,当x >0时,y随x的增大而 ,
当x= 时,取得最 值,这个值等于 ;
当a<0时,抛物线y=ax2+c的开口 ,对称轴是 ,顶点坐标是 ,当x <0时,y随x的增大而 ,当x >0时,y随x的增大而 ,当x= 时,取得最 值,这个值等于 。
y=-x2-2
y=-x2+3
y=-x2
y=x2-2
y=x2+1
y=x2
向上
y轴
(0,c)
减小
增大
0
小
c
向下
y轴
(0,c)
增大
减小
0
大
c
y=ax2+c (a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增
减
性
最值
向上
向下
(0 ,c)
(0 ,c)
y轴
y轴
当x<0时,
y随着x的增大而减小。
当x>0时,
y随着x的增大而增大。
当x<0时,
y随着x的增大而增大。
当x>0时,
y随着x的增大而减小。
x=0时,y最小=c
x=0时,y最大=c
抛物线y=ax2 +c (a≠0)的图象可由y=ax2的图象通过上下平移得到.(上加下减)
(4)抛物线y=-3x2+5的开口 ,对称轴是 ,顶点坐标是 ,在对称轴的左侧,y随x的增大而 ,在对称轴的右侧,y随x的增大而 ,
当x= 时,取得最 值,这个值等于 。
(5)抛物线y=7x2-3的开口 ,对称轴是 ,顶点坐标是 ,在对称轴的左侧,y随x的增大而 ,在对称轴的右侧,y随x的增大而 ,
当x= 时,取得最 值,这个值等于 。
下
y轴
(0,5)
减小
增大
0
大
5
上
y轴
(0,-3)
减小
增大
0
小
-3
一位篮球运动员跳起投篮,球沿抛物线
运行,然后准确落入蓝筐内,已知蓝筐的中心离地面的
距离为3.05m。
1、球在空中运行的最大高度是多少米?
2、如果运动员跳投时,球出手离地面的高度 为2.25m ,
则他离篮筐中心的水平距离AB是多少?
y=一 x2+3.5
1、(2011莆田)抛物线y=6x2 一5可以看作是抛物线y=6x2按下列何种变换得到? ( )
A、向左平移5个单位 B、向下平移5个单位
C、向右平移5个单位 D、向上平移5个单位
2 、(2011临沂)抛物线y=一x2 一5的开口方向、顶点坐标是( )
A、向上,(0,5) B 、向上,(0,一5)
C、向下,(0,5) D、向下,(0,一5)
B
D
3、抛物线y=3x2, y=一3x2,y=3x2+4共有的性质是( )
A 开口向上 B 对称轴是y轴
C 顶点坐标(0,0) D当x〉0时,y随x的增大而增大
B
(4) 函数y=ax2-a与y= (a≠0)
在同一直角坐标系中的图象可能是 ( )
A
作业:
必做题:配套P66 1、(1)(3)
2、(1)
3、
选做题:P66 1、(4)
P68 5
y=ax2 (a≠0) a>0 a<0
图
象
开口方向
顶点坐标
对称轴
增
减
性
最值
x
y
O
y
x
O
向上
向下
(0 ,0)
(0 ,0)
y轴
y轴
当x<0时,
y随着x的增大而减小。
当x>0时,
y随着x的增大而增大。
当x<0时,
y随着x的增大而增大。
当x>0时,
y随着x的增大而减小。
x=0时,y最小=0
x=0时,y最大=0
一位篮球运动员跳起投篮,球沿抛物线 y=一 x2+3.5
运行,然后准确落入蓝筐内,已知蓝筐的中心离地面的
距离为3.05m。
1、球在空中运行的最大高度是多少米?
2、如果运动员跳投时,球出手离地面的高度 为2.25m ,
则他离篮筐中心的水平距离AB是多少?
y=ax2+c的图像和性质(1)
学习目标
1、会画y=ax2+c的图像。
2、掌握y=ax2+c的性质,并能应用性质熟练解决问题。
3、体会数学由特殊到一般、数形结合的思想。
x ….. -2 -1 0 1 2 ……
y=x2 …… 4 1 0 1 4
y=x2+1 …… ……
y=x2
y=x2+1
5 2 1 2 5
函数y=x2+1的图象与y=x2的图象的位置有什么关系
函数y=x2+1的图象可由y=x2的图象沿y轴向上平移1个单位长度得到.
函数y=x2+1的图象与y=x2的图象的形状相同吗
相同
x ….. -2 -1 0 1 2 ……
y=x2 …… 4 1 0 1 4
y=x2-2 …… ……
y=x2
y=x2-2
2 -1 -2 -1 2
函数y=x2-2的图象可由y=x2的图象沿y轴向下平移2个单位长度得到.
函数y=x2-2的图象与y=x2的图象的位置有什么关系
函数y=x2+1的图象与y=x2的图象的形状相同吗
相同
函数y=ax2 (a≠0)和函数y=ax2+c (a≠0)的图象形状 ,只是位置不同;当c>0时,函数y=ax2+c的图象可由y=ax2的图象向 平移 个单位得到,当c〈0时,函数y=ax2+c的图象可由y=ax2的图象
向 平移 个单位得到。
y=-x2-2
y=-x2+3
y=-x2
函数y=-x2-2的图象可由y=-x2的图象沿y轴向下平移2个单位长度得到.
函数y=-x2+3的图象可由y=-x2的图象沿y轴向上平移3个单位长度得到.
图象向上移还是向下移,移多少个单位长度,有什么规律吗
上加下减
相同
上
c
下
|c|
(1)函数y=4x2+5的图象可由y=4x2的图象
向 平移 个单位得到;y=4x2-11的图象
可由 y=4x2的图象向 平移 个单位得到。
(3)将抛物线y=4x2向上平移3个单位,所得的
抛物线的函数式是 。
将抛物线y=-5x2+1向下平移5个单位,所得的
抛物线的函数式是 。
(2)将函数y=-3x2+4的图象向 平移 个单位可得
y=-3x2的图象;将y=2x2-7的图象向 平移 个
单位得到可由 y=2x2的图象。将y=x2-7的图象
向 平移 个单位可得到 y=x2+2的图象。
上
5
下
11
下
4
上
7
上
9
y=4x2+3
y=-5x2-4
当a>0时,抛物线y=ax2+c的开口 ,对称轴是 ,顶点坐标是 ,当x <0时,y随x的增大而 ,当x >0时,y随x的增大而 ,
当x= 时,取得最 值,这个值等于 ;
当a<0时,抛物线y=ax2+c的开口 ,对称轴是 ,顶点坐标是 ,当x <0时,y随x的增大而 ,当x >0时,y随x的增大而 ,当x= 时,取得最 值,这个值等于 。
y=-x2-2
y=-x2+3
y=-x2
y=x2-2
y=x2+1
y=x2
向上
y轴
(0,c)
减小
增大
0
小
c
向下
y轴
(0,c)
增大
减小
0
大
c
y=ax2+c (a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增
减
性
最值
向上
向下
(0 ,c)
(0 ,c)
y轴
y轴
当x<0时,
y随着x的增大而减小。
当x>0时,
y随着x的增大而增大。
当x<0时,
y随着x的增大而增大。
当x>0时,
y随着x的增大而减小。
x=0时,y最小=c
x=0时,y最大=c
抛物线y=ax2 +c (a≠0)的图象可由y=ax2的图象通过上下平移得到.(上加下减)
(4)抛物线y=-3x2+5的开口 ,对称轴是 ,顶点坐标是 ,在对称轴的左侧,y随x的增大而 ,在对称轴的右侧,y随x的增大而 ,
当x= 时,取得最 值,这个值等于 。
(5)抛物线y=7x2-3的开口 ,对称轴是 ,顶点坐标是 ,在对称轴的左侧,y随x的增大而 ,在对称轴的右侧,y随x的增大而 ,
当x= 时,取得最 值,这个值等于 。
下
y轴
(0,5)
减小
增大
0
大
5
上
y轴
(0,-3)
减小
增大
0
小
-3
一位篮球运动员跳起投篮,球沿抛物线
运行,然后准确落入蓝筐内,已知蓝筐的中心离地面的
距离为3.05m。
1、球在空中运行的最大高度是多少米?
2、如果运动员跳投时,球出手离地面的高度 为2.25m ,
则他离篮筐中心的水平距离AB是多少?
y=一 x2+3.5
1、(2011莆田)抛物线y=6x2 一5可以看作是抛物线y=6x2按下列何种变换得到? ( )
A、向左平移5个单位 B、向下平移5个单位
C、向右平移5个单位 D、向上平移5个单位
2 、(2011临沂)抛物线y=一x2 一5的开口方向、顶点坐标是( )
A、向上,(0,5) B 、向上,(0,一5)
C、向下,(0,5) D、向下,(0,一5)
B
D
3、抛物线y=3x2, y=一3x2,y=3x2+4共有的性质是( )
A 开口向上 B 对称轴是y轴
C 顶点坐标(0,0) D当x〉0时,y随x的增大而增大
B
(4) 函数y=ax2-a与y= (a≠0)
在同一直角坐标系中的图象可能是 ( )
A
作业:
必做题:配套P66 1、(1)(3)
2、(1)
3、
选做题:P66 1、(4)
P68 5
