1.2.2同角三角函数的基本关系课件-2021-2022学年高一上学期数学人教A版必修4(43张PPT)
文档属性
| 名称 | 1.2.2同角三角函数的基本关系课件-2021-2022学年高一上学期数学人教A版必修4(43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 00:00:00 | ||
图片预览










文档简介
1.2.2同角三角函数的基本关系
1.能通过三角函数的定义推导出同角三角函数的基本关系式.
2.理解同角三角函数的基本关系式.
3.能运用同角三角函数的基本关系式进行三角函数式的化简、求值和证明.
本节目标
课前预习
预习课本,思考并完成以下问题
(1)同角三角函数的基本关系式有哪两种?
(2)已知sin α,cos α和tan α其中的一个值,如何求其余两个值?
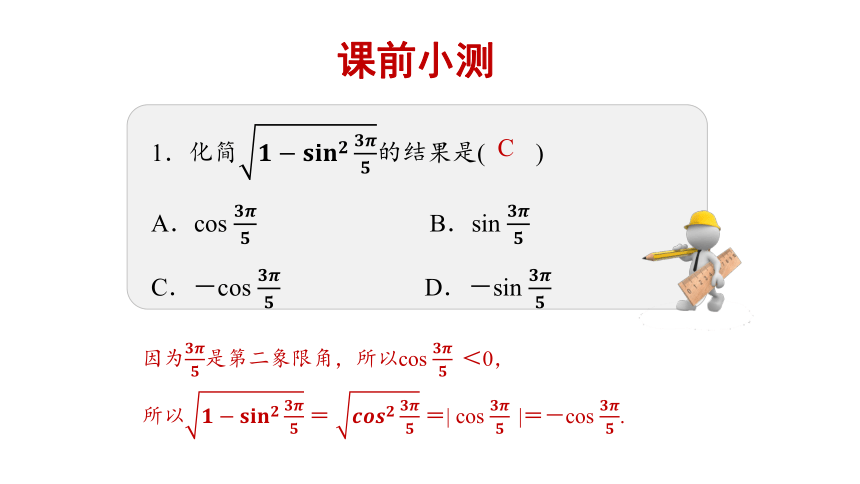
课前小测
1.化简?????????????????????????????????的结果是( )
A.cos ????????????? B.sin ????????????
C.-cos ???????????? D.-sin ????????????
?
因为????????????是第二象限角,所以cos ?????????????<0,
所以??????????????????????????????????= ?????????????????????????????=| cos ?????????????|=-cos ????????????.
?
C
2.如果α是第二象限的角,下列各式中成立的是( )
A.tan α=-????????????????????????????????
B.cos α=- ?????????????????????????
C.sin α=- ?????cos????????
D.tan α= cos????sin????
?
B
当α为第二象限角时,cos α<0,sin α>0
3.若cos α=35?,且α为第四象限角,则tan α=_____.
?
所以sin α=- ?????cos?????????=- ?????(35)?????=-45?,
?
因为α为第四象限角,且cos α= 35?,
?
所以tan α= ?????????????????????????????????=-43.
?
-43
?
新知探究
sin2α+cos2α=_______.
1.平方关系
同一个角α的正弦、余弦的平方和等于______.
1
公式
语言叙述
1
2.商数关系
公式
????????????????????????????????=________
?
语言叙述
同一个角α的正弦、余弦的商等于__________.
角α的正切
tan α
思考:对任意的角α,sin22α+cos22α=1是否成立?
提示:成立.平方关系中强调的同一个角且是任意的,与角的表达形式无关.
题型突破
典例深度剖析 重点多维探究
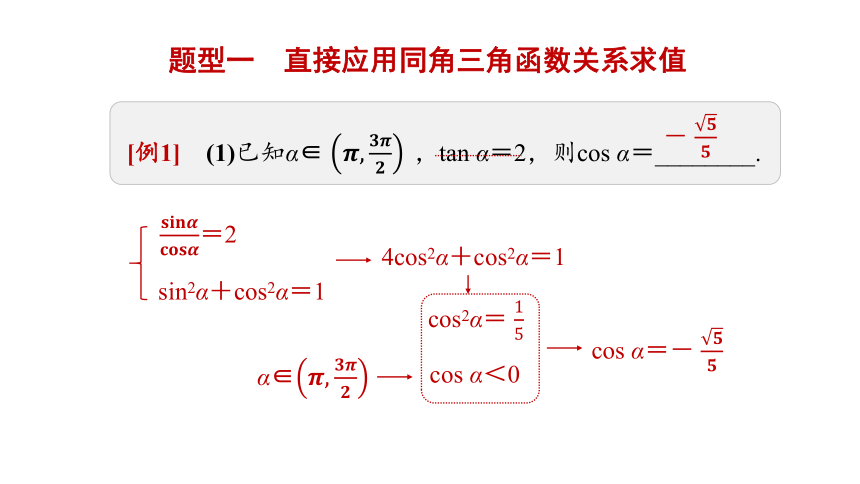
题型一 直接应用同角三角函数关系求值
[例1] (1)已知α∈ ????,?????????????,tan α=2,则cos α=________.
?
????????????????????????????????=2
?
sin2α+cos2α=1
cos α=- ????????
?
4cos2α+cos2α=1
cos2α= 15
?
α∈????,????????????
?
cos α<0
- ????????
?
[例1] (2)已知cos α=-817?,求sin α,tan α的值.
?
如果α是第三象限角,同理可得
sin α=- ?????cos?????????=- 1517?,tan α=158.
?
∵cos α=-817?<0,
?
∴α是第二或第三象限的角.
如果α是第二象限角,那么
sin α= ?????cos?????????= ?????(-817)?????= 1517?,
?
tan α= ?????????????????????????????????= 1517-817?=-158.
?
?2?若角α所在的象限已经确定,求另两种三角函数值时,只有一组结果;若角α所在的象限不确定,应分类讨论,一般有两组结果.
利用同角三角函数的基本关系解决给值求值问题的方法
?1? 已知角α的某一种三角函数值,求角α的其余三角函数值,要注意公式的合理选择,一般是先选用平方关系,再用商数关系.
易错提醒:应用平方关系求三角函数值时,要注意有关角终边位置的判断,确定所求值的符号.
方法总结
跟踪训练
1.已知sin α+3cos α=0,求sin α,cos α的值.
∵sin α+3cos α=0,∴sin α=-3cos α. 又sin2α+cos2α=1,
∴(-3cos α)2+cos2α=1,即10cos2α=1,∴cos α=±1010.
?
又由sin α=-3cos α,可知sin α与cos α异号,
∴角α的终边在第二或第四象限.
当角α的终边在第二象限时,cos α=-1010?,sin α=31010?;
当角α的终边在第四象限时,cos α=1010?,sin α=-31010.
?
题型二 灵活应用同角三角函数关系式求值
[例2] (1)已知sin α+cos α=713?,α∈(0,π),则tan α=________.
?
思路点拨
求sinαcosα
求sinα-cosα
求sinα和cosα
求tanα
法一:
法二:
求sinαcosα
弦化切构造关于tanα的方程
求tanα
题型二 灵活应用同角三角函数关系式求值
[例2] (1)已知sin α+cos α=713?,α∈(0,π),则tan α=________.
?
因为sin α+cos α= 713?,①
所以sin2α+cos2α+2sin αcos α= 49169?,即2sin αcos α=- 120169.
因为α∈(0,π),所以sin α>0,cos α<0.
所以sin α-cos α=?????????????????????????????????????= ??????????????????????????????????????????= 1713.②
?
由①②解得sin α= 1213?,cos α=- 513?,
所以tan α= ?????????????????????????????????=-125.
?
法一构建方程组
-125
?
题型二 灵活应用同角三角函数关系式求值
[例2] (1)已知sin α+cos α=713?,α∈(0,π),则tan α=________.
?
法二弦化切
-125
?
同法一求出sin αcos α=- 60169?, ????????????????????????????????sin2????+cos2?????=- 60169?,
????????????????tan2????+1?=- 60169?,整理得60tan2α+169tan α+60=0,
解得tan α=-512或tan α=- 125.
?
由sin α+cos α=713?>0知|sin α|>|cos α|,故tan α=- 125.
?
[例2] (2)已知????????????????+???????????????????????????????????????????????????=2,计算下列各式的值.
?
① 3?????????????????????????????????2????????????????+3cos??????;
?
由????????????????+???????????????????????????????????????????????????=2化简,得sin α=3cos α,所以tan α=3.
?
法二(弦化切) 原式= 3?????????????????12????????????????+3?= 3×3?12×3+3?= 89.
?
法一(换元) 原式= 3×3?????????????????????????????????2×3????????????????+3cos??????= 8????????????????9?????????????????= 89.
?
[例2] (2)已知????????????????+???????????????????????????????????????????????????=2,计算下列各式的值.
?
②sin2α-2sin αcos α+1.
原式= ????????????????????-2????????????????cos????????????????????????+?????????????????????+1
= ta????2????-2tan????????????????2????+1?+1
= 32-2×332+1?+1
= 1310
?
多维探究
变式1 已知sin α+cos α=713?,α∈(-π,0),则tan α=________.
?
由例2(1)求出2sin αcos α=-120169?,
因为α∈(-π,0),所以sin α<0,cos α>0,
所以sin α-cos α=-?????????????????????????????????????=- ??????????????????????????????????????????=-1713.
?
与sin α+cos α=713联立解得sin α=-513?,cos α= 1213?,
所以tan α= ?????????????????????????????????=-512.
?
-512
?
变式2 已知sin αcos α=-18?,α∈(0,π),则cosα-sinα=_____.
?
因为sin αcos α=-18?<0,所以α∈ (π2,π) ,所以cos α-sin α<0,
?
cos α-sin α=-??????????????????????????????????????????=-?????????×(-18)?=- ????????.
?
- ????????
?
1.sin α+cos α,sin α-cos α,sin αcos α三个式子中,已知其中一个,可以求其他两个,即“知一求二”,
它们之间的关系是:(sin α±cos α)2=1±2sin αcos α.
技法点拨
解决这类问题需注意以下两点:
(1)一定是关于sin α,cos α的齐次式(或能化为齐次式)的三角函数式;
(2)因为cos α≠0,所以可除以cos α,这样可将被求式化为关于tan α的表示式,然后代入tan α=m的值,从而完成被求式的求值.
2.已知tan α=m,求关于sin α,cos α的齐次式的值
提醒:求sin α+cos α或sin α-cos α的值,要注意根据角的终边位置,利用三角函数线判断它们的符号.
技法点拨
解决这类问题需注意以下两点:
(1)一定是关于sin α,cos α的齐次式(或能化为齐次式)的三角函数式;
(2)因为cos α≠0,所以可除以cos α,这样可将被求式化为关于tan α的表示式,然后代入tan α=m的值,从而完成被求式的求值.
已知tan α=m,求关于sin α,cos α的齐次式的值
提醒:求sin α+cos α或sin α-cos α的值,要注意根据角的终边位置,利用三角函数线判断它们的符号.
技法点拨
题型三 应用同角三角函数关系式化简
[例3] (1)化简???????????????????????????????????????????????????????????=________.
?
原式= 2sin2?????11?2(1?sin2????)?
= 2sin2?????12sin2?????1?
=1
?
1
[例3] (2)化简???????????????????????????????????????????????????????????????????????????????????????+????????????????. (其中α是第三象限角)
?
原式= ???????????????????????????????????????????????????????????????????????????????????????????????????????????????????????+????????????????
?
= ????????????????????????????????????????????????????????????????+????????????????
?
= ????????????????????????????????????????????????????????????2?????????????????2????
?
= ?????????????????????????????????????????????????????????????????????????????
?
= ?1
?
?3?对于化简含高次的三角函数式,往往借助于因式分解,或构造sin2α+cos2α=1,以降低函数次数,达到化简的目的.
三角函数式化简的常用方法
?1?化切为弦,即把正切函数都化为正、余弦函数,从而减少函数名称,达到化简的目的.
?2?对于含有根号的,常把根号里面的部分化成完全平方式,然后去根号达到化简的目的.
易错提醒:在应用平方关系式求sin α或cos α时,其正负号是由角α所在的象限决定,不可凭空想象.
技法点拨
跟踪训练
2.化简tan α ??????????????????????????????,其中α是第二象限角.
?
因为α是第二象限角,所以sin α>0,cos α<0.
故tan α ??????????????????????????????=tan α ??????????????????????????????????????????????=tan α cos?????????????????????????????
= sin????cos????·|cos????sin????|= sin????cos?????· ?cos????sin?????=-1.
?
题型四 应用同角三角函数关系式证明
1.证明三角恒等式常用哪些方法?
[探究问题]
提示:
(1)从右证到左.
(2)从左证到右.
(3)证明左右归一.
(4)变更命题法.如:欲证明????????=?????????,则可证MQ=NP,或证????????=????????等.
?
2.在证明????+????????????????+????????????????+????????????????????????????????????????+????????????????+?????????????????=sin α+cos α时如何巧用“1”的代换.
?
提示:在求证????+????????????????+????????????????+????????????????????????????????????????+????????????????+?????????????????=sin α+cos α时,观察等式左边有2sin αcos α,它和1相加应该想到“1”的代换,即1=sin2α+cos2α,
?
所以等式左边= (????????????2????+????????????2????+????????????????????????????????????)+????????????????+????????????????????+????????????????+????????????????
= ????????????????+????????????????2+????????????????+????????????????????+????????????????+????????????????= ????????????????+????????????????(1+????????????????+????????????????)????+????????????????+????????????????
=sin α+cos α=右边.
?
[例4] 求证: tan????sin????tan?????sin?????= tan????+sin????tan????sin????.
?
左边= sin2????sin?????sin????cos??????= sin????1?cos?????,
右边= sin????+sin????cos????sin2?????= 1+cos????sin????.
因为sin2α=1-cos2α=(1+cos α)(1-cos α),
所以sin????1?cos?????= 1+cos????sin?????,所以左边=右边.
所以原等式成立.
?
法一:(切化弦)
[例4] 求证: tan????sin????tan?????sin?????= tan????+sin????tan????sin????.
?
法二:(由右至左)
因为右边= tan2?????sin2????(tan?????sin????)tan????sin????
= tan2?????tan2????cos2????(tan?????sin????)tan????sin????
= tan2????(1?cos2????)(tan?????sin????)tan????sin????
= tan2????sin2????(tan?????sin????)tan????sin?????= tan????sin????tan?????sin????=左边,
所以原等式成立.
?
朝目标奔.常用的技巧有:
(1)巧用“1”的代换;
(2)化切为弦;
(3)多项式运算技巧的应用(分解因式).
1.证明恒等式常用的思路
(1)从一边证到另一边,一般由繁到简;
(2)左右开弓,即证左边、右边都等于第三者;
(3)比较法(作差,作比法).
2.技巧感悟
提醒:解决此类问题要有整体代换思想.
方法技巧
跟踪训练
3.求证:(1) sin?????cos????+1sin????+cos?????1?= 1+sin????cos?????;
?
左边= (sin?????cos????+1)(sin????+cos????+1)(sin????+cos?????1)(sin????+cos????+1)
= sin????+12?cos2????(sin????+cos????)2?1
?
= sin2????+2sin????+1?(1?sin2????)sin2????+cos2????+2sin????cos?????1
?
= 2sin2????+2sin????1+2sin????cos?????1
?
= 2sin????(sin????+1)2sin????cos????
?
= sin????+1cos????
?
所以原等式成立.
=右边
3.求证:(2) 2(sin6 θ+cos6 θ)-3(sin4 θ+cos4 θ)+1=0.
左边=2[(sin2 θ)3+(cos2 θ)3]-3(sin4 θ+cos4 θ)+1
=2(sin2 θ+cos2 θ)(sin4 θ-sin2 θcos2 θ+cos4 θ)-3(sin4 θ+cos4 θ)+1
=(2sin4 θ-2sin2 θcos2 θ+2cos4 θ)-(3sin4 θ+3cos4 θ)+1
=-(sin4 θ+2sin2 θcos2 θ+cos4 θ)+1
=-(sin2 θ+cos2 θ)2+1=-1+1=0=右边,
∴原等式成立.
随堂检测
(2)因为sin294π+cos2 π4 =1,所以sin2α+cos2β=1成立,其中α,β为任意角.( )
?
1.思考辨析
(1)对任意角α, ????????????????????????????????????????=????????????????????都成立.( )
?
(3)对任意角α,sin α=cos α·tan α都成立.( )
×
×
×
2.已知tan α=-1?????,则2sin????cos????sin2?????cos2?????的值是( )
A. 43? B.3 C.-43? D.-3
?
2sin????cos????sin2?????cos2????? = 2tan????tan2?????1
?
= 2×(?1????)?1????2?1
?
= 43
?
A
3.已知α是第二象限角,tan α=-1?????,则cos α=________.
?
因为sin????cos?????=-1?????,且sin2α+cos2α=1,
又因为α是第二象限角,
所以cos α<0,
所以cos α=-????????????.
?
?????????????
?
4.(1)化简??????????????????????????????????????????,其中α是第二象限角.
?
因为α是第二象限角,所以sin α>0,cos α<0,
所以sin αcos α<0,
所以??????????????????????????????????????????= ????????????????????(1?sin2????)
= ????????????????????cos2????)
=-sin αcos α.
?
4. (2)求证:1+tan2α= ????????????????????????.
?
1+tan2α=1+????in?????????????????????????????
= ????????????????????+????in??????????????????????????????
= ????????????????????????
?
本课小结
1.能通过三角函数的定义推导出同角三角函数的基本关系式.
2.理解同角三角函数的基本关系式.
3.能运用同角三角函数的基本关系式进行三角函数式的化简、求值和证明.
本节目标
课前预习
预习课本,思考并完成以下问题
(1)同角三角函数的基本关系式有哪两种?
(2)已知sin α,cos α和tan α其中的一个值,如何求其余两个值?
课前小测
1.化简?????????????????????????????????的结果是( )
A.cos ????????????? B.sin ????????????
C.-cos ???????????? D.-sin ????????????
?
因为????????????是第二象限角,所以cos ?????????????<0,
所以??????????????????????????????????= ?????????????????????????????=| cos ?????????????|=-cos ????????????.
?
C
2.如果α是第二象限的角,下列各式中成立的是( )
A.tan α=-????????????????????????????????
B.cos α=- ?????????????????????????
C.sin α=- ?????cos????????
D.tan α= cos????sin????
?
B
当α为第二象限角时,cos α<0,sin α>0
3.若cos α=35?,且α为第四象限角,则tan α=_____.
?
所以sin α=- ?????cos?????????=- ?????(35)?????=-45?,
?
因为α为第四象限角,且cos α= 35?,
?
所以tan α= ?????????????????????????????????=-43.
?
-43
?
新知探究
sin2α+cos2α=_______.
1.平方关系
同一个角α的正弦、余弦的平方和等于______.
1
公式
语言叙述
1
2.商数关系
公式
????????????????????????????????=________
?
语言叙述
同一个角α的正弦、余弦的商等于__________.
角α的正切
tan α
思考:对任意的角α,sin22α+cos22α=1是否成立?
提示:成立.平方关系中强调的同一个角且是任意的,与角的表达形式无关.
题型突破
典例深度剖析 重点多维探究
题型一 直接应用同角三角函数关系求值
[例1] (1)已知α∈ ????,?????????????,tan α=2,则cos α=________.
?
????????????????????????????????=2
?
sin2α+cos2α=1
cos α=- ????????
?
4cos2α+cos2α=1
cos2α= 15
?
α∈????,????????????
?
cos α<0
- ????????
?
[例1] (2)已知cos α=-817?,求sin α,tan α的值.
?
如果α是第三象限角,同理可得
sin α=- ?????cos?????????=- 1517?,tan α=158.
?
∵cos α=-817?<0,
?
∴α是第二或第三象限的角.
如果α是第二象限角,那么
sin α= ?????cos?????????= ?????(-817)?????= 1517?,
?
tan α= ?????????????????????????????????= 1517-817?=-158.
?
?2?若角α所在的象限已经确定,求另两种三角函数值时,只有一组结果;若角α所在的象限不确定,应分类讨论,一般有两组结果.
利用同角三角函数的基本关系解决给值求值问题的方法
?1? 已知角α的某一种三角函数值,求角α的其余三角函数值,要注意公式的合理选择,一般是先选用平方关系,再用商数关系.
易错提醒:应用平方关系求三角函数值时,要注意有关角终边位置的判断,确定所求值的符号.
方法总结
跟踪训练
1.已知sin α+3cos α=0,求sin α,cos α的值.
∵sin α+3cos α=0,∴sin α=-3cos α. 又sin2α+cos2α=1,
∴(-3cos α)2+cos2α=1,即10cos2α=1,∴cos α=±1010.
?
又由sin α=-3cos α,可知sin α与cos α异号,
∴角α的终边在第二或第四象限.
当角α的终边在第二象限时,cos α=-1010?,sin α=31010?;
当角α的终边在第四象限时,cos α=1010?,sin α=-31010.
?
题型二 灵活应用同角三角函数关系式求值
[例2] (1)已知sin α+cos α=713?,α∈(0,π),则tan α=________.
?
思路点拨
求sinαcosα
求sinα-cosα
求sinα和cosα
求tanα
法一:
法二:
求sinαcosα
弦化切构造关于tanα的方程
求tanα
题型二 灵活应用同角三角函数关系式求值
[例2] (1)已知sin α+cos α=713?,α∈(0,π),则tan α=________.
?
因为sin α+cos α= 713?,①
所以sin2α+cos2α+2sin αcos α= 49169?,即2sin αcos α=- 120169.
因为α∈(0,π),所以sin α>0,cos α<0.
所以sin α-cos α=?????????????????????????????????????= ??????????????????????????????????????????= 1713.②
?
由①②解得sin α= 1213?,cos α=- 513?,
所以tan α= ?????????????????????????????????=-125.
?
法一构建方程组
-125
?
题型二 灵活应用同角三角函数关系式求值
[例2] (1)已知sin α+cos α=713?,α∈(0,π),则tan α=________.
?
法二弦化切
-125
?
同法一求出sin αcos α=- 60169?, ????????????????????????????????sin2????+cos2?????=- 60169?,
????????????????tan2????+1?=- 60169?,整理得60tan2α+169tan α+60=0,
解得tan α=-512或tan α=- 125.
?
由sin α+cos α=713?>0知|sin α|>|cos α|,故tan α=- 125.
?
[例2] (2)已知????????????????+???????????????????????????????????????????????????=2,计算下列各式的值.
?
① 3?????????????????????????????????2????????????????+3cos??????;
?
由????????????????+???????????????????????????????????????????????????=2化简,得sin α=3cos α,所以tan α=3.
?
法二(弦化切) 原式= 3?????????????????12????????????????+3?= 3×3?12×3+3?= 89.
?
法一(换元) 原式= 3×3?????????????????????????????????2×3????????????????+3cos??????= 8????????????????9?????????????????= 89.
?
[例2] (2)已知????????????????+???????????????????????????????????????????????????=2,计算下列各式的值.
?
②sin2α-2sin αcos α+1.
原式= ????????????????????-2????????????????cos????????????????????????+?????????????????????+1
= ta????2????-2tan????????????????2????+1?+1
= 32-2×332+1?+1
= 1310
?
多维探究
变式1 已知sin α+cos α=713?,α∈(-π,0),则tan α=________.
?
由例2(1)求出2sin αcos α=-120169?,
因为α∈(-π,0),所以sin α<0,cos α>0,
所以sin α-cos α=-?????????????????????????????????????=- ??????????????????????????????????????????=-1713.
?
与sin α+cos α=713联立解得sin α=-513?,cos α= 1213?,
所以tan α= ?????????????????????????????????=-512.
?
-512
?
变式2 已知sin αcos α=-18?,α∈(0,π),则cosα-sinα=_____.
?
因为sin αcos α=-18?<0,所以α∈ (π2,π) ,所以cos α-sin α<0,
?
cos α-sin α=-??????????????????????????????????????????=-?????????×(-18)?=- ????????.
?
- ????????
?
1.sin α+cos α,sin α-cos α,sin αcos α三个式子中,已知其中一个,可以求其他两个,即“知一求二”,
它们之间的关系是:(sin α±cos α)2=1±2sin αcos α.
技法点拨
解决这类问题需注意以下两点:
(1)一定是关于sin α,cos α的齐次式(或能化为齐次式)的三角函数式;
(2)因为cos α≠0,所以可除以cos α,这样可将被求式化为关于tan α的表示式,然后代入tan α=m的值,从而完成被求式的求值.
2.已知tan α=m,求关于sin α,cos α的齐次式的值
提醒:求sin α+cos α或sin α-cos α的值,要注意根据角的终边位置,利用三角函数线判断它们的符号.
技法点拨
解决这类问题需注意以下两点:
(1)一定是关于sin α,cos α的齐次式(或能化为齐次式)的三角函数式;
(2)因为cos α≠0,所以可除以cos α,这样可将被求式化为关于tan α的表示式,然后代入tan α=m的值,从而完成被求式的求值.
已知tan α=m,求关于sin α,cos α的齐次式的值
提醒:求sin α+cos α或sin α-cos α的值,要注意根据角的终边位置,利用三角函数线判断它们的符号.
技法点拨
题型三 应用同角三角函数关系式化简
[例3] (1)化简???????????????????????????????????????????????????????????=________.
?
原式= 2sin2?????11?2(1?sin2????)?
= 2sin2?????12sin2?????1?
=1
?
1
[例3] (2)化简???????????????????????????????????????????????????????????????????????????????????????+????????????????. (其中α是第三象限角)
?
原式= ???????????????????????????????????????????????????????????????????????????????????????????????????????????????????????+????????????????
?
= ????????????????????????????????????????????????????????????????+????????????????
?
= ????????????????????????????????????????????????????????????2?????????????????2????
?
= ?????????????????????????????????????????????????????????????????????????????
?
= ?1
?
?3?对于化简含高次的三角函数式,往往借助于因式分解,或构造sin2α+cos2α=1,以降低函数次数,达到化简的目的.
三角函数式化简的常用方法
?1?化切为弦,即把正切函数都化为正、余弦函数,从而减少函数名称,达到化简的目的.
?2?对于含有根号的,常把根号里面的部分化成完全平方式,然后去根号达到化简的目的.
易错提醒:在应用平方关系式求sin α或cos α时,其正负号是由角α所在的象限决定,不可凭空想象.
技法点拨
跟踪训练
2.化简tan α ??????????????????????????????,其中α是第二象限角.
?
因为α是第二象限角,所以sin α>0,cos α<0.
故tan α ??????????????????????????????=tan α ??????????????????????????????????????????????=tan α cos?????????????????????????????
= sin????cos????·|cos????sin????|= sin????cos?????· ?cos????sin?????=-1.
?
题型四 应用同角三角函数关系式证明
1.证明三角恒等式常用哪些方法?
[探究问题]
提示:
(1)从右证到左.
(2)从左证到右.
(3)证明左右归一.
(4)变更命题法.如:欲证明????????=?????????,则可证MQ=NP,或证????????=????????等.
?
2.在证明????+????????????????+????????????????+????????????????????????????????????????+????????????????+?????????????????=sin α+cos α时如何巧用“1”的代换.
?
提示:在求证????+????????????????+????????????????+????????????????????????????????????????+????????????????+?????????????????=sin α+cos α时,观察等式左边有2sin αcos α,它和1相加应该想到“1”的代换,即1=sin2α+cos2α,
?
所以等式左边= (????????????2????+????????????2????+????????????????????????????????????)+????????????????+????????????????????+????????????????+????????????????
= ????????????????+????????????????2+????????????????+????????????????????+????????????????+????????????????= ????????????????+????????????????(1+????????????????+????????????????)????+????????????????+????????????????
=sin α+cos α=右边.
?
[例4] 求证: tan????sin????tan?????sin?????= tan????+sin????tan????sin????.
?
左边= sin2????sin?????sin????cos??????= sin????1?cos?????,
右边= sin????+sin????cos????sin2?????= 1+cos????sin????.
因为sin2α=1-cos2α=(1+cos α)(1-cos α),
所以sin????1?cos?????= 1+cos????sin?????,所以左边=右边.
所以原等式成立.
?
法一:(切化弦)
[例4] 求证: tan????sin????tan?????sin?????= tan????+sin????tan????sin????.
?
法二:(由右至左)
因为右边= tan2?????sin2????(tan?????sin????)tan????sin????
= tan2?????tan2????cos2????(tan?????sin????)tan????sin????
= tan2????(1?cos2????)(tan?????sin????)tan????sin????
= tan2????sin2????(tan?????sin????)tan????sin?????= tan????sin????tan?????sin????=左边,
所以原等式成立.
?
朝目标奔.常用的技巧有:
(1)巧用“1”的代换;
(2)化切为弦;
(3)多项式运算技巧的应用(分解因式).
1.证明恒等式常用的思路
(1)从一边证到另一边,一般由繁到简;
(2)左右开弓,即证左边、右边都等于第三者;
(3)比较法(作差,作比法).
2.技巧感悟
提醒:解决此类问题要有整体代换思想.
方法技巧
跟踪训练
3.求证:(1) sin?????cos????+1sin????+cos?????1?= 1+sin????cos?????;
?
左边= (sin?????cos????+1)(sin????+cos????+1)(sin????+cos?????1)(sin????+cos????+1)
= sin????+12?cos2????(sin????+cos????)2?1
?
= sin2????+2sin????+1?(1?sin2????)sin2????+cos2????+2sin????cos?????1
?
= 2sin2????+2sin????1+2sin????cos?????1
?
= 2sin????(sin????+1)2sin????cos????
?
= sin????+1cos????
?
所以原等式成立.
=右边
3.求证:(2) 2(sin6 θ+cos6 θ)-3(sin4 θ+cos4 θ)+1=0.
左边=2[(sin2 θ)3+(cos2 θ)3]-3(sin4 θ+cos4 θ)+1
=2(sin2 θ+cos2 θ)(sin4 θ-sin2 θcos2 θ+cos4 θ)-3(sin4 θ+cos4 θ)+1
=(2sin4 θ-2sin2 θcos2 θ+2cos4 θ)-(3sin4 θ+3cos4 θ)+1
=-(sin4 θ+2sin2 θcos2 θ+cos4 θ)+1
=-(sin2 θ+cos2 θ)2+1=-1+1=0=右边,
∴原等式成立.
随堂检测
(2)因为sin294π+cos2 π4 =1,所以sin2α+cos2β=1成立,其中α,β为任意角.( )
?
1.思考辨析
(1)对任意角α, ????????????????????????????????????????=????????????????????都成立.( )
?
(3)对任意角α,sin α=cos α·tan α都成立.( )
×
×
×
2.已知tan α=-1?????,则2sin????cos????sin2?????cos2?????的值是( )
A. 43? B.3 C.-43? D.-3
?
2sin????cos????sin2?????cos2????? = 2tan????tan2?????1
?
= 2×(?1????)?1????2?1
?
= 43
?
A
3.已知α是第二象限角,tan α=-1?????,则cos α=________.
?
因为sin????cos?????=-1?????,且sin2α+cos2α=1,
又因为α是第二象限角,
所以cos α<0,
所以cos α=-????????????.
?
?????????????
?
4.(1)化简??????????????????????????????????????????,其中α是第二象限角.
?
因为α是第二象限角,所以sin α>0,cos α<0,
所以sin αcos α<0,
所以??????????????????????????????????????????= ????????????????????(1?sin2????)
= ????????????????????cos2????)
=-sin αcos α.
?
4. (2)求证:1+tan2α= ????????????????????????.
?
1+tan2α=1+????in?????????????????????????????
= ????????????????????+????in??????????????????????????????
= ????????????????????????
?
本课小结
