1.3集合间的基本运算 课件——2021-2022学年高一上学期数学人教A版(2019)必修第一册(共24张PPT)
文档属性
| 名称 | 1.3集合间的基本运算 课件——2021-2022学年高一上学期数学人教A版(2019)必修第一册(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-21 22:49:05 | ||
图片预览








文档简介
(共24张PPT)
第一章集合与常用逻辑用语
1.3集合的基本运算
2021
01
并集
交集
补集
利用集合间的关系求参数
课堂总结
02
03
04
05
CONTENTS
目录
问题
某兴趣小组有20名学生,学号分别是1,2,3,…,20,现新到a,b两本新书,
已知学号是偶数的读过新书a,学号是3的倍数的读过新书b.
(1) 至少读过一本书的有哪些学生?
(2) 同时读了a,b两本书的有哪些学生?
(3) 一本书也没有读的有哪些学生?
(1) 至少读过一本书的学生有2,3,4,6,8,9,10,12,14,15,16,18,20.
(2) 同时读了a,b两本书的学生有6,12,18.
(3) 一本书也没有读的学生有1,5,7,11,13,17,19.
01
并集
思考
考察下列各个集合,你能说出集合C与集合A、B之间的关系吗?
(1) A={1,3,5}, B={2,4,6}, C={1,2,3,4,5,6}.
(2) A={x|x是有理数}, B={x|x是无理数}, C={x|x是实数}.
并集
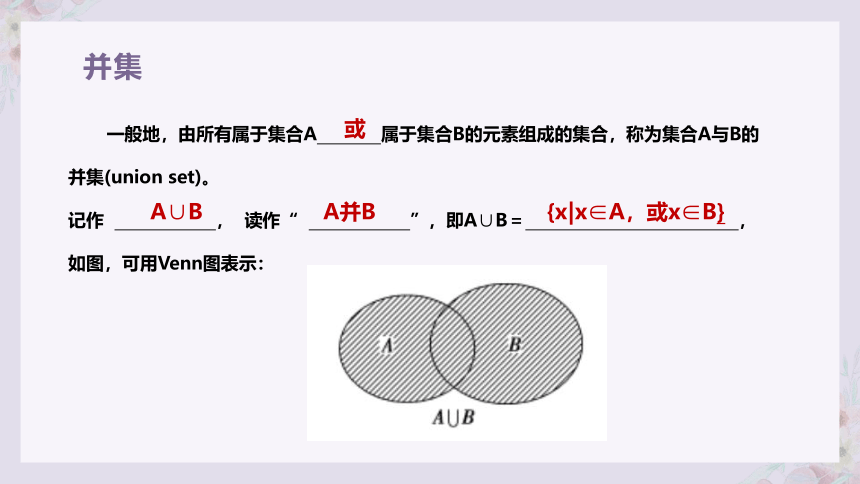
一般地,由所有属于集合A 属于集合B的元素组成的集合,称为集合A与B的并集(union set)。
记作 , 读作“ ”,即A∪B= ,
如图,可用Venn图表示:
或
A并B
{x|x∈A,或x∈B}
A∪B
并集
例1.若集合M={-1,0,1},集合N={0,1,2},则M∪N=( )
A.{0,1} B.{-1,0,1}
C.{0,1,2} D.{-1,0,1,2}
D
02
交集
思考
考察下列各个集合,集合C与集合A、B之间有什么关系吗?
(1) A={2,4,6,8,10}, B={3,5,8,12}, C={8}.
(2)A={x|x是立德中学今年在校的女同学},
B={x|x是立德中学今年在校的高一年级同学},
C={x|x是立德中学今年在校的高一年级女同学}.
交集
一般地,由所有属于集合A 属于集合B的元素组成的集合,称为集合A与B的交集(intersection set)。
记作 ,读作 ,即A∩B= ,
如图,可用Venn图表示:
A∩B
且
A交B
{x|x∈A,且x∈B}
交集
例2.已知集合A={0,2},B={-2,-1,0,1,2},则A∩B=( )
A.{0,2} B.{1,2}
C.{0} D.{-2,-1,0,1,2}
A
集合的交并运算
(1) 已知集合A={x|(x-1)(x+2)=0},B={x|(x+2)(x-3)=0},则集合A∪B是( )
A.{-1,2,3} B.{-1,-2,3} C.{1,-2,3} D.{1,-2,-3}
(2) 若集合A={x|-2≤x<3},B={x|0≤x<4},则A∪B=_____.
(1)A={1,-2},B={-2,3},∴A∪B={1,-2,3}.
(2)将-2≤x<3与0≤x<4在数轴上表示出来.
根据并集的定义,图中阴影部分即为所求,∴A∪B={x|-2≤x<4}.
解析:
03
补集
思考
A={高一(1)班参加足球队的同学},B={高一(1)班没有参加足球队的同学},
U={高一(1)班的同学}.
(1) 集合A,B,U有何关系?
(2) B中元素与U和A有何关系?
U=A∪B
B中的元素在U中,不在A中
全集 补集
对于一个集合A,由全集中 集合A的所有元素组成的集合称为集合A相对于全集U的补集(complementary set),简称为集合A的补集,记作 ,即 = ,可用Venn图表示:
一般地,如果一个集合含有所研究问题中涉及的 元素,那么就称这个集合为全集(universe set),通常记作 .
不属于
{x|x∈U,且x A}
所有
U
补集
例3.设U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},
求
解析: 根据题意可知: U={1,2,3,4,5,6,7,8},
所以
={4,5,6,7,8},
= {1,2,7,8}.
C
例4.已知U=R,集合A={x|x<-2,或x>2},则 =( )
A.{x|-2<x<2} B.{x|x<-2或x>2}
C.{x|-2≤x≤2} D.{x|x≤-2或x≥2}
补集
解析:
根据补集的定义并结合数轴可得
={x|-2≤x≤2}.
补集
解析:
将集合U和集合A分别表示在数轴上,如图所示:
由补集定义可得 ={x|x<-3或x=5}.
例5.已知全集U={x|x≤5},集合A={x|-3≤x<5},则 =________.
并集、交集、补集的综合运算
把全集U和集合A,B在数轴上表示如下:
={x|x≤-2或3≤x≤4},A∩B={x|-2={x|x≤-2或3≤x≤4},
( )∩B={x|-3解析:
例6. 已知全集U={x|x≤4},集合A={x|-2求 ,A∩B, ,( )∩B.
04
利用集合间的关系求参数
利用集合间的关系求参数
解析:
由已知A={x|x≥-m},得 ={x|x<-m},
因为B={x|-2<x<4},( )∩B= ,
在数轴上表示如图
所以-m≤-2,即m≥2,所以m的取值范围是m≥2.
例7. 设集合A={x|x+m≥0},B={x|-2<x<4},全集U=R,且( )∩B= , 求实数m的取值范围.
例8.已知全集U=R,集合A={x|-2≤x≤5},B={x|a+1≤x≤2a-1}A UB,
求实数a的取值范围.
解析:
若B= ,则a+1>2a-1,则a<2,此时 UB=R,∴A UB;
若B≠ ,则a+1≤2a-1,即a≥2,此时 UB={x|x2a-1},
由于A UB,如图,
则a+1>5,∴a>4,
∴实数a的取值范围为{a|a<2,或a>4}.
利用集合间的关系求参数
课堂总结
Thanks.
第一章集合与常用逻辑用语
1.3集合的基本运算
2021
01
并集
交集
补集
利用集合间的关系求参数
课堂总结
02
03
04
05
CONTENTS
目录
问题
某兴趣小组有20名学生,学号分别是1,2,3,…,20,现新到a,b两本新书,
已知学号是偶数的读过新书a,学号是3的倍数的读过新书b.
(1) 至少读过一本书的有哪些学生?
(2) 同时读了a,b两本书的有哪些学生?
(3) 一本书也没有读的有哪些学生?
(1) 至少读过一本书的学生有2,3,4,6,8,9,10,12,14,15,16,18,20.
(2) 同时读了a,b两本书的学生有6,12,18.
(3) 一本书也没有读的学生有1,5,7,11,13,17,19.
01
并集
思考
考察下列各个集合,你能说出集合C与集合A、B之间的关系吗?
(1) A={1,3,5}, B={2,4,6}, C={1,2,3,4,5,6}.
(2) A={x|x是有理数}, B={x|x是无理数}, C={x|x是实数}.
并集
一般地,由所有属于集合A 属于集合B的元素组成的集合,称为集合A与B的并集(union set)。
记作 , 读作“ ”,即A∪B= ,
如图,可用Venn图表示:
或
A并B
{x|x∈A,或x∈B}
A∪B
并集
例1.若集合M={-1,0,1},集合N={0,1,2},则M∪N=( )
A.{0,1} B.{-1,0,1}
C.{0,1,2} D.{-1,0,1,2}
D
02
交集
思考
考察下列各个集合,集合C与集合A、B之间有什么关系吗?
(1) A={2,4,6,8,10}, B={3,5,8,12}, C={8}.
(2)A={x|x是立德中学今年在校的女同学},
B={x|x是立德中学今年在校的高一年级同学},
C={x|x是立德中学今年在校的高一年级女同学}.
交集
一般地,由所有属于集合A 属于集合B的元素组成的集合,称为集合A与B的交集(intersection set)。
记作 ,读作 ,即A∩B= ,
如图,可用Venn图表示:
A∩B
且
A交B
{x|x∈A,且x∈B}
交集
例2.已知集合A={0,2},B={-2,-1,0,1,2},则A∩B=( )
A.{0,2} B.{1,2}
C.{0} D.{-2,-1,0,1,2}
A
集合的交并运算
(1) 已知集合A={x|(x-1)(x+2)=0},B={x|(x+2)(x-3)=0},则集合A∪B是( )
A.{-1,2,3} B.{-1,-2,3} C.{1,-2,3} D.{1,-2,-3}
(2) 若集合A={x|-2≤x<3},B={x|0≤x<4},则A∪B=_____.
(1)A={1,-2},B={-2,3},∴A∪B={1,-2,3}.
(2)将-2≤x<3与0≤x<4在数轴上表示出来.
根据并集的定义,图中阴影部分即为所求,∴A∪B={x|-2≤x<4}.
解析:
03
补集
思考
A={高一(1)班参加足球队的同学},B={高一(1)班没有参加足球队的同学},
U={高一(1)班的同学}.
(1) 集合A,B,U有何关系?
(2) B中元素与U和A有何关系?
U=A∪B
B中的元素在U中,不在A中
全集 补集
对于一个集合A,由全集中 集合A的所有元素组成的集合称为集合A相对于全集U的补集(complementary set),简称为集合A的补集,记作 ,即 = ,可用Venn图表示:
一般地,如果一个集合含有所研究问题中涉及的 元素,那么就称这个集合为全集(universe set),通常记作 .
不属于
{x|x∈U,且x A}
所有
U
补集
例3.设U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},
求
解析: 根据题意可知: U={1,2,3,4,5,6,7,8},
所以
={4,5,6,7,8},
= {1,2,7,8}.
C
例4.已知U=R,集合A={x|x<-2,或x>2},则 =( )
A.{x|-2<x<2} B.{x|x<-2或x>2}
C.{x|-2≤x≤2} D.{x|x≤-2或x≥2}
补集
解析:
根据补集的定义并结合数轴可得
={x|-2≤x≤2}.
补集
解析:
将集合U和集合A分别表示在数轴上,如图所示:
由补集定义可得 ={x|x<-3或x=5}.
例5.已知全集U={x|x≤5},集合A={x|-3≤x<5},则 =________.
并集、交集、补集的综合运算
把全集U和集合A,B在数轴上表示如下:
={x|x≤-2或3≤x≤4},A∩B={x|-2
( )∩B={x|-3
例6. 已知全集U={x|x≤4},集合A={x|-2
04
利用集合间的关系求参数
利用集合间的关系求参数
解析:
由已知A={x|x≥-m},得 ={x|x<-m},
因为B={x|-2<x<4},( )∩B= ,
在数轴上表示如图
所以-m≤-2,即m≥2,所以m的取值范围是m≥2.
例7. 设集合A={x|x+m≥0},B={x|-2<x<4},全集U=R,且( )∩B= , 求实数m的取值范围.
例8.已知全集U=R,集合A={x|-2≤x≤5},B={x|a+1≤x≤2a-1}A UB,
求实数a的取值范围.
解析:
若B= ,则a+1>2a-1,则a<2,此时 UB=R,∴A UB;
若B≠ ,则a+1≤2a-1,即a≥2,此时 UB={x|x
由于A UB,如图,
则a+1>5,∴a>4,
∴实数a的取值范围为{a|a<2,或a>4}.
利用集合间的关系求参数
课堂总结
Thanks.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
