1.3三角函数的诱导公式课件(2)--2021-2022学年高一上学期数学人教A版必修4(35张PPT)
文档属性
| 名称 | 1.3三角函数的诱导公式课件(2)--2021-2022学年高一上学期数学人教A版必修4(35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 00:00:00 | ||
图片预览











文档简介
1.3 诱导公式(2)
1.掌握诱导公式五、六的推导,并能应用于解决简单的求值、化简与证明问题.
2.对诱导公式一至六,能作综合归纳,体会出六组公式的共性与个性,培养由特殊到一般的数学推理意识和能力.
本节目标
课前预习
预习课本,思考并完成以下问题
(1) ?????????-α的终边与α的终边有怎样的对称关系?
(2) 诱导公式五、六有哪些结构特征?
?
课前小测
1.下列与sin θ的值相等的是( )
A.sin(π+θ) B.sin ?????????????
C.cos ????????????? D.cos ????????+????
?
C
sin(π+θ)=-sin θ;sin ??????????????=cos θ;
cos ??????????????=sin θ;cos ????????+?????=-sin θ.
?
2.已知sin 19°55′=m,则cos(-70°5′)=________.
cos(-70°5′)=cos 70°5′
=cos(90°-19°55′)
=sin 19°55′
=m.
m
3.计算:sin211°+sin279°=________.
原式=sin211°+cos211°=1
11°+79°=90°
sin 79°=cos 11°
1
4.化简sin(???????????? +α)=________.
?
sin(???????????? +α) = sin(????+???????? +α)
?
= -sin(???????? +α)
?
= -cos α
-cos α
新知探究
1.公式五
(1)角????????-α与角α的终边关于_________对称,如图所示.
?
直线y=x
sin(????????-α)=_______,
cos (????????-α) =_______.
?
cosα
sinα
(2)公式
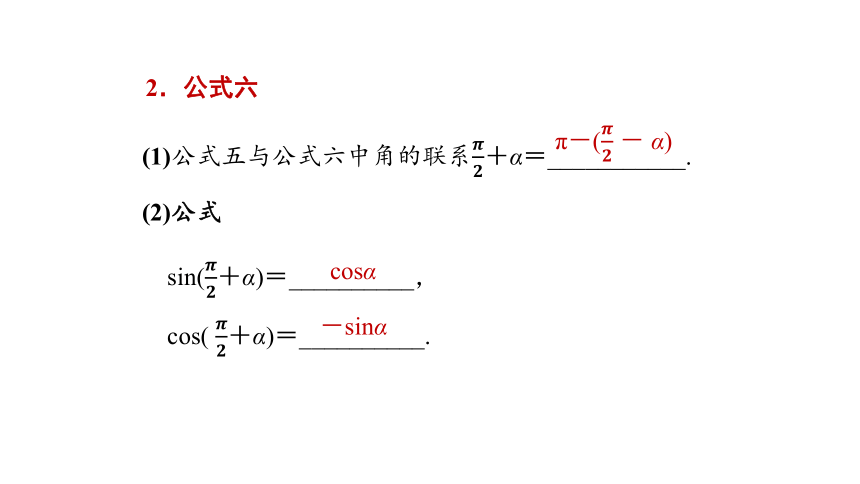
2.公式六
(1)公式五与公式六中角的联系????????+α=___________.
?
π-(???????? - α)
?
(2)公式
sin(????????+α)=__________,
cos( ????????+α)=__________.
?
cosα
-sinα
思考:如何由公式四及公式五推导公式六?
提示:
sin (????????+α) =sin[π-(???????? - α)]
=sin (???????? - α)=cos α.
cos (????????+α) =cos[π-(???????? - α)]
=-cos (???????? - α) =-sin α.
?
题型突破
典例深度剖析 重点多维探究
题型一 利用诱导公式化简求值
[例1] (1)已知cos 31°=m,则sin 239°tan 149°的值是( )
A. ?????????????????? B. ?????????????
C.-????????????????? D.-?????????????
?
sin 239°tan 149°=sin(180°+59°)·tan(180°-31°)=-sin 59°(-tan 31°)
=-sin(90°-31°)·(-tan 31°)=-cos 31°·(-tan 31°)=sin 31°
= ???????????????????????????????= ?????????????
?
B
(2)已知sin(????3-α)=12?,则cos (????6+α)的值为________.
?
cos (????6+α)
=cos [???????? -(????3-α)]
=sin (????3-α)
= 12
?
12
?
多维探究
变式1 已知sin(????3+α)=12?,则cos (5????6+α)的值为______.
?
cos (5????6+α)
?
=cos (????2 + ????3+α)
?
= -sin (????3+α)
?
= -12
?
-12
?
变式2 已知sin(????3-α)=12?,α是第二象限角,求sin (7????6+α)的值.
?
因为α是第二象限角,所以-α是第三象限角,
又sin (????3-α)= 12?,所以????3?-α是第二象限角,
所以cos (????3-α) =- ?????????,
所以sin (7????6+α) =sin (????+????6+α) =-sin(????6+????)=-cos (????3-α) = ?????????
?
注意
?1?首先要仔细观察条件与所求式之间的角、函数名称及有关运算之间的差异及联系.
常见的互余关系有: ????3?-α与????6?+α, ????4?-α与????4?+α等.
常见的互补关系有: ????3?+????与2????3-????, ????4?+????与3????4-????等.
?
解决化简求值问题的策略
解题策略
?2?可以将已知式进行变形,向所求式转化,或将所求式进行变形,向已知式转化.
题型二 利用诱导公式证明恒等式
[例2] (1)求证: ????????????????+?????????????????????????????????????????????????=?????????????????????????????????????????????????+??????????????????????????????????????????+????.
(2)求证: ????????????????????+???????????????????????????????????????????????????????????????????????????????+????????????????????????????+????=?????????????????.
?
[例2] (1)求证: ????????????????+?????????????????????????????????????????????????=?????????????????????????????????????????????????+??????????????????????????????????????????+????.
?
右边= ??????????????????????????????????(?sin????)??????????????????????????????????
?
= ????????????????[????+(????2-????)]sin??????????????????????????????????????
?
= ?????????????????(????2-????)sin??????????????????????????????????????
?
= ?????????????????????sin?????????????????????????????+cos2??????????????????????????????
?
= ????????????????+????????????????2?????????????????????cos2????
?
= ????????????????+?????????????????????????????????????????????????
?
=左边
[例2] (2)求证: ????????????????????+???????????????????????????????????????????????????????????????????????????????+????????????????????????????+????=?????????????????.
?
左边= ??????????????????????????????????????????????????????????????????????+????????????????????????+????
?
= ?????????????????????????????????????????????????????????????????????????????????
?
=?????????????????
?
=右边
?1?遵循的原则:在证明时一般从左边到右边,或从右边到左边,或左右归一,总之,应遵循化繁为简的原则.
?2?常用的方法:定义法,化弦法,拆项拆角法,公式变形法,“1”的代换法.
三角恒等式的证明的策略
解题策略
跟踪训练
1.求证: ????????????????????????+???????????????????????????????????????????????????????????=-1.
?
左边= ????????????2????+????????+??????????????????????????????2?????????????????????
?
= ????????????????????+??????????????????????????????????????????????
?
= ?????in????????????????????????????????????
?
=-1
=右边
题型三 诱导公式的综合应用
1.公式一~四和公式五~六的主要区别是什么?
[探究问题]
提示:
公式一~四中函数名称不变,公式五~六中函数名称改变.
题型三 诱导公式的综合应用
2.如何用一个口诀描述应用诱导公式化简三角函数式的过程?
[探究问题]
提示:
“奇变偶不变、符号看象限”
[例3] 已知sin α是方程5x2-7x-6=0的根,α是第三象限角,求????????????????????????????????????????????????????????????????????????????????????????????????????????+?????·tan2(π-α)的值.
?
方程5x2-7x-6=0的两根为x1=-35?,x2=2,
因为-1≤sin α≤1,所以sin α=-35.
又α是第三象限角,所以cos α=-45?,tan α= sin?????cos??????= 34?,
所以????????????????????????????????????????????????????????????????????????????????????????????????????????+?????·tan2(π-α) = ?????????????????????????????????????????????+????sin??????cos???????·tan2α
?
= cos?????(?sin?????)sin?????cos??????·tan2α
?
= ?tan2α
?
= ?916
?
一看角:①化大为小;②看角与角间的联系,可通过相加、相减分析两角的关系.
诱导公式综合应用要“三看”
二看函数名称:一般是弦切互化.
三看式子结构:通过分析式子,选择合适的方法,如分式可对分子分母同乘一个式子变形.
技法点拨
跟踪训练
2.已知sin ???????????????·cos ?5??????????????= 60169?,且????4<α<?????????,求sin α与cos α的值.
?
sin ??????????????=?cos?????
?
cos ?5?????????????=cos 2????+????????+????=?sin?????
?
sin?????·cos?????= 60169
?
2sin?????·cos?????= 120169
?
①+②得(sin α+cos α)2= 289169?,
?
①
又∵sin2α+cos2α=1,②
又∵α∈(????4,????????),∴sin α>cos α>0,
?
②-①得(sin α-cos α)2= 49169.
?
跟踪训练
2.已知sin ???????????????·cos ?5??????????????= 60169?,且????4<α<?????????,求sin α与cos α的值.
?
即sin α+cos α>0,sin α-cos α>0,
∴sin α+cos α= 1713?,③
sin α-cos α= 713?,④
(③+④)÷2得sin α= 1213?,(③-④)÷2得cos α= 513.
?
随堂检测
(1)公式五和公式六中的角α一定是锐角.( )
(2)在△ABC中,sin ????+?????????=cos ????2.( )
(3)sin????????+????=sin?????????(?????)=cos(-α)=cos α.( )
?
1.思考辨析
×
√
√
任意角
????+????????+ ????2 = ????2
?
2.若sin ????????+?????<0,且cos ??????????????>0,则θ是( )
A.第一象限角 B.第二象限角
C.第三角限角 D.第四象限角
?
sin????????+?????=cos θ<0,cos ??????????????=sin θ>0
所以角θ的终边落在第二象限
?
B
3.已知cos α=15?,且α为第四象限角,那么cos ????+?????????=________.
?
所以cos ????+?????????=-sin α= ????????????.
?
????????????
?
因为cos α= 15?,且α为第四象限角,
?
所以sin α=- ??????????????????????????=- ?????????????,
?
4.化简: ?????????????????????????????????????????????+????????????????????+????????????????????????????????????????????????????????????????????????????.
?
原式= cos?????(-sin?????)-cos??????- sin(?????)sin?????sin?????
=sin α-(-sin α)
=2sin α
?
本课小结
1.公式五反映了终边关于直线y=x对称的角的正、余弦函数值之间的关系,其中角????????-α的正弦(余弦)函数值,等于角α的余弦(正弦)函数值.
?
2.由于?????????+α=π-(????????-α),因此由公式四及公式五可以得到公式六.
?
3.利用诱导公式可在三角函数的变形过程中进行角的转化.在求任意角的过程中,一般先把负角转化为正角,正角转化为0~2π的范围内的角,再将这个范围内的角转化为锐角.也就是“负化正,大化小,化到锐角再查表(特殊角的三角函数值表)”.
本课小结
1.掌握诱导公式五、六的推导,并能应用于解决简单的求值、化简与证明问题.
2.对诱导公式一至六,能作综合归纳,体会出六组公式的共性与个性,培养由特殊到一般的数学推理意识和能力.
本节目标
课前预习
预习课本,思考并完成以下问题
(1) ?????????-α的终边与α的终边有怎样的对称关系?
(2) 诱导公式五、六有哪些结构特征?
?
课前小测
1.下列与sin θ的值相等的是( )
A.sin(π+θ) B.sin ?????????????
C.cos ????????????? D.cos ????????+????
?
C
sin(π+θ)=-sin θ;sin ??????????????=cos θ;
cos ??????????????=sin θ;cos ????????+?????=-sin θ.
?
2.已知sin 19°55′=m,则cos(-70°5′)=________.
cos(-70°5′)=cos 70°5′
=cos(90°-19°55′)
=sin 19°55′
=m.
m
3.计算:sin211°+sin279°=________.
原式=sin211°+cos211°=1
11°+79°=90°
sin 79°=cos 11°
1
4.化简sin(???????????? +α)=________.
?
sin(???????????? +α) = sin(????+???????? +α)
?
= -sin(???????? +α)
?
= -cos α
-cos α
新知探究
1.公式五
(1)角????????-α与角α的终边关于_________对称,如图所示.
?
直线y=x
sin(????????-α)=_______,
cos (????????-α) =_______.
?
cosα
sinα
(2)公式
2.公式六
(1)公式五与公式六中角的联系????????+α=___________.
?
π-(???????? - α)
?
(2)公式
sin(????????+α)=__________,
cos( ????????+α)=__________.
?
cosα
-sinα
思考:如何由公式四及公式五推导公式六?
提示:
sin (????????+α) =sin[π-(???????? - α)]
=sin (???????? - α)=cos α.
cos (????????+α) =cos[π-(???????? - α)]
=-cos (???????? - α) =-sin α.
?
题型突破
典例深度剖析 重点多维探究
题型一 利用诱导公式化简求值
[例1] (1)已知cos 31°=m,则sin 239°tan 149°的值是( )
A. ?????????????????? B. ?????????????
C.-????????????????? D.-?????????????
?
sin 239°tan 149°=sin(180°+59°)·tan(180°-31°)=-sin 59°(-tan 31°)
=-sin(90°-31°)·(-tan 31°)=-cos 31°·(-tan 31°)=sin 31°
= ???????????????????????????????= ?????????????
?
B
(2)已知sin(????3-α)=12?,则cos (????6+α)的值为________.
?
cos (????6+α)
=cos [???????? -(????3-α)]
=sin (????3-α)
= 12
?
12
?
多维探究
变式1 已知sin(????3+α)=12?,则cos (5????6+α)的值为______.
?
cos (5????6+α)
?
=cos (????2 + ????3+α)
?
= -sin (????3+α)
?
= -12
?
-12
?
变式2 已知sin(????3-α)=12?,α是第二象限角,求sin (7????6+α)的值.
?
因为α是第二象限角,所以-α是第三象限角,
又sin (????3-α)= 12?,所以????3?-α是第二象限角,
所以cos (????3-α) =- ?????????,
所以sin (7????6+α) =sin (????+????6+α) =-sin(????6+????)=-cos (????3-α) = ?????????
?
注意
?1?首先要仔细观察条件与所求式之间的角、函数名称及有关运算之间的差异及联系.
常见的互余关系有: ????3?-α与????6?+α, ????4?-α与????4?+α等.
常见的互补关系有: ????3?+????与2????3-????, ????4?+????与3????4-????等.
?
解决化简求值问题的策略
解题策略
?2?可以将已知式进行变形,向所求式转化,或将所求式进行变形,向已知式转化.
题型二 利用诱导公式证明恒等式
[例2] (1)求证: ????????????????+?????????????????????????????????????????????????=?????????????????????????????????????????????????+??????????????????????????????????????????+????.
(2)求证: ????????????????????+???????????????????????????????????????????????????????????????????????????????+????????????????????????????+????=?????????????????.
?
[例2] (1)求证: ????????????????+?????????????????????????????????????????????????=?????????????????????????????????????????????????+??????????????????????????????????????????+????.
?
右边= ??????????????????????????????????(?sin????)??????????????????????????????????
?
= ????????????????[????+(????2-????)]sin??????????????????????????????????????
?
= ?????????????????(????2-????)sin??????????????????????????????????????
?
= ?????????????????????sin?????????????????????????????+cos2??????????????????????????????
?
= ????????????????+????????????????2?????????????????????cos2????
?
= ????????????????+?????????????????????????????????????????????????
?
=左边
[例2] (2)求证: ????????????????????+???????????????????????????????????????????????????????????????????????????????+????????????????????????????+????=?????????????????.
?
左边= ??????????????????????????????????????????????????????????????????????+????????????????????????+????
?
= ?????????????????????????????????????????????????????????????????????????????????
?
=?????????????????
?
=右边
?1?遵循的原则:在证明时一般从左边到右边,或从右边到左边,或左右归一,总之,应遵循化繁为简的原则.
?2?常用的方法:定义法,化弦法,拆项拆角法,公式变形法,“1”的代换法.
三角恒等式的证明的策略
解题策略
跟踪训练
1.求证: ????????????????????????+???????????????????????????????????????????????????????????=-1.
?
左边= ????????????2????+????????+??????????????????????????????2?????????????????????
?
= ????????????????????+??????????????????????????????????????????????
?
= ?????in????????????????????????????????????
?
=-1
=右边
题型三 诱导公式的综合应用
1.公式一~四和公式五~六的主要区别是什么?
[探究问题]
提示:
公式一~四中函数名称不变,公式五~六中函数名称改变.
题型三 诱导公式的综合应用
2.如何用一个口诀描述应用诱导公式化简三角函数式的过程?
[探究问题]
提示:
“奇变偶不变、符号看象限”
[例3] 已知sin α是方程5x2-7x-6=0的根,α是第三象限角,求????????????????????????????????????????????????????????????????????????????????????????????????????????+?????·tan2(π-α)的值.
?
方程5x2-7x-6=0的两根为x1=-35?,x2=2,
因为-1≤sin α≤1,所以sin α=-35.
又α是第三象限角,所以cos α=-45?,tan α= sin?????cos??????= 34?,
所以????????????????????????????????????????????????????????????????????????????????????????????????????????+?????·tan2(π-α) = ?????????????????????????????????????????????+????sin??????cos???????·tan2α
?
= cos?????(?sin?????)sin?????cos??????·tan2α
?
= ?tan2α
?
= ?916
?
一看角:①化大为小;②看角与角间的联系,可通过相加、相减分析两角的关系.
诱导公式综合应用要“三看”
二看函数名称:一般是弦切互化.
三看式子结构:通过分析式子,选择合适的方法,如分式可对分子分母同乘一个式子变形.
技法点拨
跟踪训练
2.已知sin ???????????????·cos ?5??????????????= 60169?,且????4<α<?????????,求sin α与cos α的值.
?
sin ??????????????=?cos?????
?
cos ?5?????????????=cos 2????+????????+????=?sin?????
?
sin?????·cos?????= 60169
?
2sin?????·cos?????= 120169
?
①+②得(sin α+cos α)2= 289169?,
?
①
又∵sin2α+cos2α=1,②
又∵α∈(????4,????????),∴sin α>cos α>0,
?
②-①得(sin α-cos α)2= 49169.
?
跟踪训练
2.已知sin ???????????????·cos ?5??????????????= 60169?,且????4<α<?????????,求sin α与cos α的值.
?
即sin α+cos α>0,sin α-cos α>0,
∴sin α+cos α= 1713?,③
sin α-cos α= 713?,④
(③+④)÷2得sin α= 1213?,(③-④)÷2得cos α= 513.
?
随堂检测
(1)公式五和公式六中的角α一定是锐角.( )
(2)在△ABC中,sin ????+?????????=cos ????2.( )
(3)sin????????+????=sin?????????(?????)=cos(-α)=cos α.( )
?
1.思考辨析
×
√
√
任意角
????+????????+ ????2 = ????2
?
2.若sin ????????+?????<0,且cos ??????????????>0,则θ是( )
A.第一象限角 B.第二象限角
C.第三角限角 D.第四象限角
?
sin????????+?????=cos θ<0,cos ??????????????=sin θ>0
所以角θ的终边落在第二象限
?
B
3.已知cos α=15?,且α为第四象限角,那么cos ????+?????????=________.
?
所以cos ????+?????????=-sin α= ????????????.
?
????????????
?
因为cos α= 15?,且α为第四象限角,
?
所以sin α=- ??????????????????????????=- ?????????????,
?
4.化简: ?????????????????????????????????????????????+????????????????????+????????????????????????????????????????????????????????????????????????????.
?
原式= cos?????(-sin?????)-cos??????- sin(?????)sin?????sin?????
=sin α-(-sin α)
=2sin α
?
本课小结
1.公式五反映了终边关于直线y=x对称的角的正、余弦函数值之间的关系,其中角????????-α的正弦(余弦)函数值,等于角α的余弦(正弦)函数值.
?
2.由于?????????+α=π-(????????-α),因此由公式四及公式五可以得到公式六.
?
3.利用诱导公式可在三角函数的变形过程中进行角的转化.在求任意角的过程中,一般先把负角转化为正角,正角转化为0~2π的范围内的角,再将这个范围内的角转化为锐角.也就是“负化正,大化小,化到锐角再查表(特殊角的三角函数值表)”.
本课小结
