4.4.1对数函数题型归纳练习-2021-2022学年高一上学期数学人教A版(2019)必修第一册(Word含答案)
文档属性
| 名称 | 4.4.1对数函数题型归纳练习-2021-2022学年高一上学期数学人教A版(2019)必修第一册(Word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 535.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-21 23:03:47 | ||
图片预览



文档简介
对数函数
对数函数的概念
对数函数的概念(基本形式、基本计算、待定系数法)
例:
(1)下列函数是对数函数的是( )
A.y=ln x B.y=ln(x+1)
C.y=logxe D.y=logxx
(2)给出下列函数:
① ;② ;③ ;④ .
其中是对数函数的有( )
A.1个 B.2个 C.3个 D.4个
(3)对数函数的图像过点M(125,3),则此对数函数的解析式为( )
A.y=log5x B.y= C.y= D.y=log3x
(4)已知函数,则______.
(5)已知对数函数则_______.
(6)若函数是对数函数,则 .
对数函数有关的函数定义域(求定义域、由定义域求参数范围)
例:
(7)函数f(x)=的定义域为______.
(8)函数的定义域为__________.
(9)求函数的定义域.
(10)若函数的定义域为,则( )
A.1 B.-1 C.2 D.无法确定
(11)已知函数(,且),若当时,函数恒有意义,求实数的取值范围.
(12)已知函数的定义域为,求实数的取值范围.
对数函数的图像和性质
对数函数图像(基本图像与参数关系、图像的变换、凹凸性)
例:
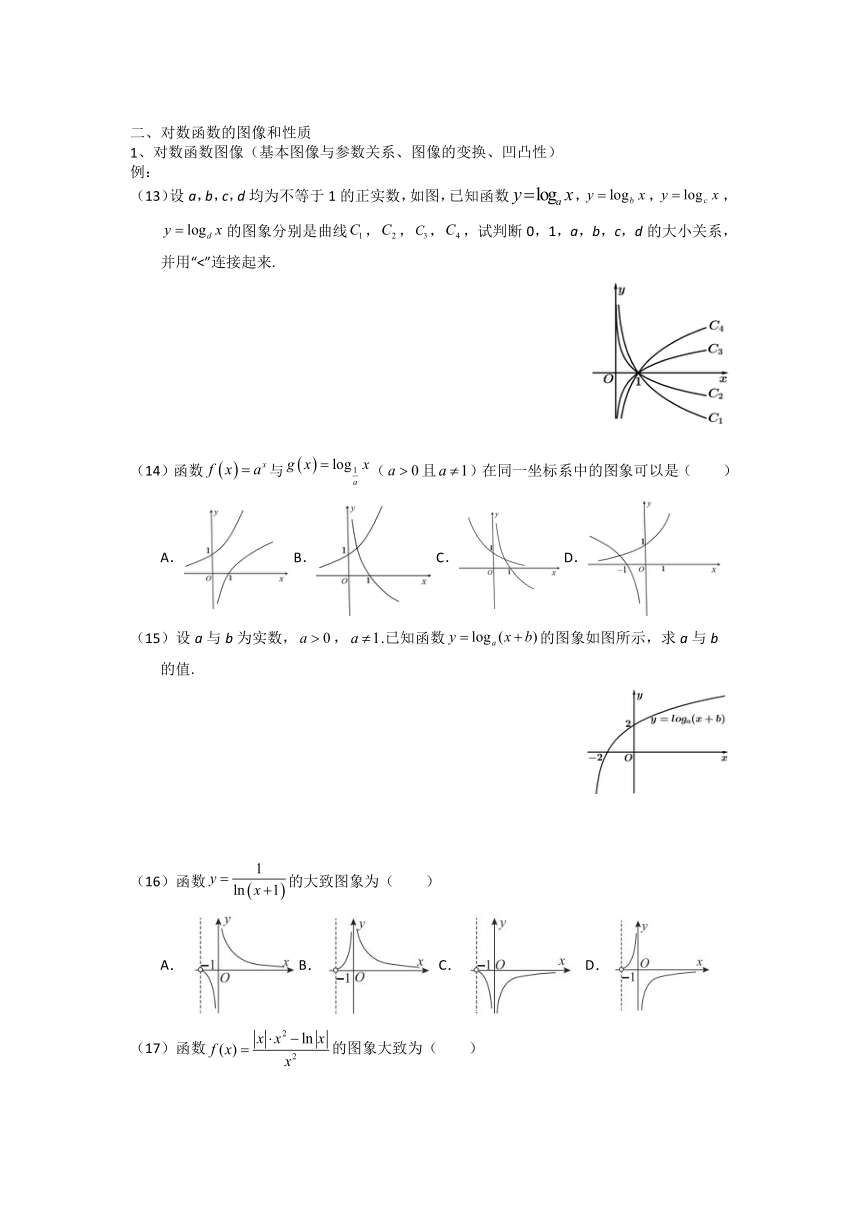
(13)设a,b,c,d均为不等于1的正实数,如图,已知函数,,,的图象分别是曲线,,,,试判断0,1,a,b,c,d的大小关系,并用“<”连接起来.
(14)函数与(且)在同一坐标系中的图象可以是( )
A.B.C.D.
(15)设a与b为实数,,.已知函数的图象如图所示,求a与b的值.
(16)函数的大致图象为( )
A.B.C. D.
(17)函数的图象大致为( )
A.B.C.D.
对数函数恒过某点
例:
(18)函数的图象过定点______.
(19)函数y=loga(x+1)-2(a>0且a≠1)的图象恒过点________.
对数函数单调性(解不等式、比较数值大小、求参数范围、求单调区间注意定义域限制)
例:
(20)求函数f(x)=lg(x2-2x-3)的单调递减区间( )
A. B. C. D.
(21)若,,,则下列结论正确的是( )
A. B. C. D.
(22)设实数,且,,,则x,y,z的大小关系为( )
A. B.
C. D.
(23)已知函数,若,,,则( )
A. B. C. D.
(24)解不等式:;
(25)设函数则满足的的取值范围是( )
A. B. C. D.
(26)已知在区间上单调递减,则实数的取值范围是_____.
(27)已知函数对任意两个不相等的实数,,都满足不等式,则实数的取值范围是________.
(28)若函数在区间上单调递增,则实数的取值范围为___________.
(29)已知函数在上单调递减,则实数a的取值范围是( )
A. B. C. D.
(30)若关于的不等式在区间上有解,则实数的取值范围为( )
A. B. C. D.
对数函数与奇偶性
例:
(31)已知定义在上的函数(为实数)为偶函数,记,,,则,,的大小关系为( )
A. B. C. D.
(32)下列函数中,既是偶函数又在区间上单调递增的函数是( )
A. B. C. D.
(33)(多选题)已知是偶函数,在上是减函数,则下列给出的的取值范围中,能使得成立的有( )
A. B. C. D.
(34)设为奇函数,为常数.
① 求的值;
② 若对于上的每一个的值,不等式恒成立,求实数的取值范围.
对数函数的值域
例:
(35)函数在区间上的最大值为______,最小值为______.
(36)已知函数的值域为,定义域为,则的最大值为______.
(37)若函数(且)有最大值,则的取值范围是___________.
(38)函数的值域为,则实数的取值范围是____________.
(39)已知函数,若存在最小值,则实数的取值范围是( )
A. B. C. D.
(40)已知函数区间上恒有,则实数a的取值范围是( )
A. B. C. D.
反函数
例:
(41)已知函数为函数的反函数,且函数的图象经过点,则函数的图象一定经过点___________.
(42)函数的反函数为___________.
(43)已知函数的反函数为,则___________.
(44)记函数的反函数为,如果函数的图象过点,那么函数的图象一定过点___________.
(45)函数()的反函数是___________.
三、不同函数增长的差异(增长差异、实际图像问题、实际问题函数模型)
例:
(46)某种植物生长发育的数量y与时间x的关系如下表:
x 1 2 3 …
y 1 2 5 …
下面的函数关系式中,能表达这种关系的是( )
A.y=log2(x+1) B.y=2x-1 C.y=2x-1 D.y=(x-1)2+1
(47)植物研究者在研究某种植物1-5年内的植株高度时,将得到的数据用下图直观表示.现要根据这些数据用一个函数模型来描述这种植物在1-5年内的生长规律,下列函数模型中符合要求的是( )
A.(且 )
B.(,且 )
C. D.
(48)下面对函数,与在区间上的递减情况说法正确的是( )
A.递减速度越来越慢,递减速度越来越快,递减速度比较平稳
B.递减速度越来越快,递减速度越来越慢,递减速度越来越快
C.递减速度越来越慢,递减速度越来越慢,递减速度比较平稳
D.递减速度越来越快,递减速度越来越快,递减速度越来越快
(49)四人赛跑,假设其跑过的路程和时间的函数关系分别是:①,②,③,④.如果他们一直跑下去,最终跑在最前面的人具有的函数关系是____.(只要填序号)
(50)以下四种说法中,正确的是( )
A.幂函数增长的速度比一次函数增长的速度快
B.对任意的x>0,xn>logax
C.对任意的x>0,ax>logax
D.不一定存在x0,当x>x0时,总有ax>xn>logax
(51)水以恒速注入下图所示容器中,则水的高度与时间的函数关系是( )
A.B.C.D.
(52)学校宿舍与办公室相距,某同学有重要材料要送给老师,从宿舍出发先匀速跑步3分钟来到办公室,停留2分钟,然后匀速步行10分钟返回宿舍.在这个过程中,这位同学行走的路程是时间的函数,则这个函数图象是( )
A. B.
C. D.
(53)生活经验告诉我们,当水注进容器(设单位时间内进水量相同)时,水的高度随着时间的变化而变化,在下图中请选择与容器相匹配的图像,A对应________;B对应________;C对应________;D对应________.
(54)某地土豆开始上市.通过市场调查得到土豆种植成本元/吨与上市时间天的数据如下表:
时间 50 110 120
种植成本 150 108 150
① 根据上表数据,从下列函数中选取一个函数描述西红柿种植成本与上市时间的变化关系.(,,,)
② 利用你选取的函数,求土豆种植成本最低时的上市天数及最低种植成本.
(55)土豆学名马铃薯,与稻、麦、玉米、高粱一起被称为全球五大农作物.云南人爱吃土豆,在云南土豆也称洋芋,昆明人常说“吃洋芋,长子弟”.年月,在全国两会的代表通道里,云南农业大学名誉校长朱有勇院士,举着一个两公斤的土豆,向全国的媒体展示,为来自家乡的“山货”代言,他自豪地说:“北京人吃的醋溜土豆丝,盘里有盘是我们澜沧种的!”
① 在菜市上,听到小王叫卖:“洋芋便宜卖了,两元一斤,三元两斤,四元三斤,五元四斤,六元五斤,快来买啊!”结果一群人都在买六元五斤的.由此得到如下结论:一次购买的斤数越多,单价越低,请建立一个函数模型,来说明以上结论;
② 小王卖洋芋赚到了钱,想进行某个项目的投资,约定如下:①投资金额固定;②投资年数可自由选择,但最短年,最长不超过年;③投资年数与总回报的关系,可选择下述三种方案中的一种:方案一:当时, ,以后每增加时,增加;方案二:;方案三:.请你根据以上材料,结合你的分析,为小王提供一个最佳投资方案.
参考答案
A
A
A
3
5
(0,]
B
或
B
,
A
D
(0,-2)
A
A
C
C
D
C
A
C
B
AC
① ;②
3;1
D
A
1
D
B
C
④
D
A
A
(4) (1) (3) (2)
① ;② 土豆种植成本最低时的上市天数是第天,最低种植成本为元/吨
① ;② 投资3-5年时,选方案一;投资6年时,选方案一或方案二;投资7-8年时,选方案二;投资9年时,选方案二或方案三;投资10年时,选方案三.
对数函数的概念
对数函数的概念(基本形式、基本计算、待定系数法)
例:
(1)下列函数是对数函数的是( )
A.y=ln x B.y=ln(x+1)
C.y=logxe D.y=logxx
(2)给出下列函数:
① ;② ;③ ;④ .
其中是对数函数的有( )
A.1个 B.2个 C.3个 D.4个
(3)对数函数的图像过点M(125,3),则此对数函数的解析式为( )
A.y=log5x B.y= C.y= D.y=log3x
(4)已知函数,则______.
(5)已知对数函数则_______.
(6)若函数是对数函数,则 .
对数函数有关的函数定义域(求定义域、由定义域求参数范围)
例:
(7)函数f(x)=的定义域为______.
(8)函数的定义域为__________.
(9)求函数的定义域.
(10)若函数的定义域为,则( )
A.1 B.-1 C.2 D.无法确定
(11)已知函数(,且),若当时,函数恒有意义,求实数的取值范围.
(12)已知函数的定义域为,求实数的取值范围.
对数函数的图像和性质
对数函数图像(基本图像与参数关系、图像的变换、凹凸性)
例:
(13)设a,b,c,d均为不等于1的正实数,如图,已知函数,,,的图象分别是曲线,,,,试判断0,1,a,b,c,d的大小关系,并用“<”连接起来.
(14)函数与(且)在同一坐标系中的图象可以是( )
A.B.C.D.
(15)设a与b为实数,,.已知函数的图象如图所示,求a与b的值.
(16)函数的大致图象为( )
A.B.C. D.
(17)函数的图象大致为( )
A.B.C.D.
对数函数恒过某点
例:
(18)函数的图象过定点______.
(19)函数y=loga(x+1)-2(a>0且a≠1)的图象恒过点________.
对数函数单调性(解不等式、比较数值大小、求参数范围、求单调区间注意定义域限制)
例:
(20)求函数f(x)=lg(x2-2x-3)的单调递减区间( )
A. B. C. D.
(21)若,,,则下列结论正确的是( )
A. B. C. D.
(22)设实数,且,,,则x,y,z的大小关系为( )
A. B.
C. D.
(23)已知函数,若,,,则( )
A. B. C. D.
(24)解不等式:;
(25)设函数则满足的的取值范围是( )
A. B. C. D.
(26)已知在区间上单调递减,则实数的取值范围是_____.
(27)已知函数对任意两个不相等的实数,,都满足不等式,则实数的取值范围是________.
(28)若函数在区间上单调递增,则实数的取值范围为___________.
(29)已知函数在上单调递减,则实数a的取值范围是( )
A. B. C. D.
(30)若关于的不等式在区间上有解,则实数的取值范围为( )
A. B. C. D.
对数函数与奇偶性
例:
(31)已知定义在上的函数(为实数)为偶函数,记,,,则,,的大小关系为( )
A. B. C. D.
(32)下列函数中,既是偶函数又在区间上单调递增的函数是( )
A. B. C. D.
(33)(多选题)已知是偶函数,在上是减函数,则下列给出的的取值范围中,能使得成立的有( )
A. B. C. D.
(34)设为奇函数,为常数.
① 求的值;
② 若对于上的每一个的值,不等式恒成立,求实数的取值范围.
对数函数的值域
例:
(35)函数在区间上的最大值为______,最小值为______.
(36)已知函数的值域为,定义域为,则的最大值为______.
(37)若函数(且)有最大值,则的取值范围是___________.
(38)函数的值域为,则实数的取值范围是____________.
(39)已知函数,若存在最小值,则实数的取值范围是( )
A. B. C. D.
(40)已知函数区间上恒有,则实数a的取值范围是( )
A. B. C. D.
反函数
例:
(41)已知函数为函数的反函数,且函数的图象经过点,则函数的图象一定经过点___________.
(42)函数的反函数为___________.
(43)已知函数的反函数为,则___________.
(44)记函数的反函数为,如果函数的图象过点,那么函数的图象一定过点___________.
(45)函数()的反函数是___________.
三、不同函数增长的差异(增长差异、实际图像问题、实际问题函数模型)
例:
(46)某种植物生长发育的数量y与时间x的关系如下表:
x 1 2 3 …
y 1 2 5 …
下面的函数关系式中,能表达这种关系的是( )
A.y=log2(x+1) B.y=2x-1 C.y=2x-1 D.y=(x-1)2+1
(47)植物研究者在研究某种植物1-5年内的植株高度时,将得到的数据用下图直观表示.现要根据这些数据用一个函数模型来描述这种植物在1-5年内的生长规律,下列函数模型中符合要求的是( )
A.(且 )
B.(,且 )
C. D.
(48)下面对函数,与在区间上的递减情况说法正确的是( )
A.递减速度越来越慢,递减速度越来越快,递减速度比较平稳
B.递减速度越来越快,递减速度越来越慢,递减速度越来越快
C.递减速度越来越慢,递减速度越来越慢,递减速度比较平稳
D.递减速度越来越快,递减速度越来越快,递减速度越来越快
(49)四人赛跑,假设其跑过的路程和时间的函数关系分别是:①,②,③,④.如果他们一直跑下去,最终跑在最前面的人具有的函数关系是____.(只要填序号)
(50)以下四种说法中,正确的是( )
A.幂函数增长的速度比一次函数增长的速度快
B.对任意的x>0,xn>logax
C.对任意的x>0,ax>logax
D.不一定存在x0,当x>x0时,总有ax>xn>logax
(51)水以恒速注入下图所示容器中,则水的高度与时间的函数关系是( )
A.B.C.D.
(52)学校宿舍与办公室相距,某同学有重要材料要送给老师,从宿舍出发先匀速跑步3分钟来到办公室,停留2分钟,然后匀速步行10分钟返回宿舍.在这个过程中,这位同学行走的路程是时间的函数,则这个函数图象是( )
A. B.
C. D.
(53)生活经验告诉我们,当水注进容器(设单位时间内进水量相同)时,水的高度随着时间的变化而变化,在下图中请选择与容器相匹配的图像,A对应________;B对应________;C对应________;D对应________.
(54)某地土豆开始上市.通过市场调查得到土豆种植成本元/吨与上市时间天的数据如下表:
时间 50 110 120
种植成本 150 108 150
① 根据上表数据,从下列函数中选取一个函数描述西红柿种植成本与上市时间的变化关系.(,,,)
② 利用你选取的函数,求土豆种植成本最低时的上市天数及最低种植成本.
(55)土豆学名马铃薯,与稻、麦、玉米、高粱一起被称为全球五大农作物.云南人爱吃土豆,在云南土豆也称洋芋,昆明人常说“吃洋芋,长子弟”.年月,在全国两会的代表通道里,云南农业大学名誉校长朱有勇院士,举着一个两公斤的土豆,向全国的媒体展示,为来自家乡的“山货”代言,他自豪地说:“北京人吃的醋溜土豆丝,盘里有盘是我们澜沧种的!”
① 在菜市上,听到小王叫卖:“洋芋便宜卖了,两元一斤,三元两斤,四元三斤,五元四斤,六元五斤,快来买啊!”结果一群人都在买六元五斤的.由此得到如下结论:一次购买的斤数越多,单价越低,请建立一个函数模型,来说明以上结论;
② 小王卖洋芋赚到了钱,想进行某个项目的投资,约定如下:①投资金额固定;②投资年数可自由选择,但最短年,最长不超过年;③投资年数与总回报的关系,可选择下述三种方案中的一种:方案一:当时, ,以后每增加时,增加;方案二:;方案三:.请你根据以上材料,结合你的分析,为小王提供一个最佳投资方案.
参考答案
A
A
A
3
5
(0,]
B
或
B
,
A
D
(0,-2)
A
A
C
C
D
C
A
C
B
AC
① ;②
3;1
D
A
1
D
B
C
④
D
A
A
(4) (1) (3) (2)
① ;② 土豆种植成本最低时的上市天数是第天,最低种植成本为元/吨
① ;② 投资3-5年时,选方案一;投资6年时,选方案一或方案二;投资7-8年时,选方案二;投资9年时,选方案二或方案三;投资10年时,选方案三.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
