高一上学期物理人教版(2019)必修第一册第二章 匀变速直线运动的规律 尖子生培优卷(word版含答案)
文档属性
| 名称 | 高一上学期物理人教版(2019)必修第一册第二章 匀变速直线运动的规律 尖子生培优卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 691.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-11-21 08:19:09 | ||
图片预览




文档简介
第2章 匀变速直线运动的规律 尖子生培优卷
一、单选题。本大题共8小题,每小题5分,共40分,每小题只有一个选项符合题意。
1.蹦床是一项专业运动员利用蹦床的反弹效果表现技巧的竞技运动,属体操项目之一。朱雪莹在东京奥运会夺冠一跳如图所示。某段过程中,她自距水平网面高3.2m处由静止下落,与网作用0.5s后,竖直向上弹离水平网面的最大高度为5m,若忽略触网过程中蹬网发力动作而将其视为质点,不计空气阻力且规定竖直向下为正方向, 。下列说法正确的是( )
A.她下落到刚接触网面时的速度为10m/s
B.她自最高点向下运动到最低点的过程历时0.8s
C.她与网作用过程中的平均加速度为-4m/s2
D.她自静止下落到弹回至最高点的过程中,平均速度为
2.2021年10月1日,新中国迎来72周年华诞.天安门广场鲜艳的五星红旗冉冉升起!升旗手要在两分零七秒的时间内分秒不差的将国旗从旗杆底升到杆顶。现将升旗过程简化为:先做初速度为零的匀加速运动,再做匀速运动,最后匀减速运动到零。已知国旗上升的高度为28.3m,国旗在匀速阶段的速度可能为( )
A.0.20m/s B.0.30m/s C.0.50m/s D.0.60m/s
3.一物体在摩擦力作用下在水平地面上匀减速滑动,若已知物体在第1s内的位移为8m,在第3内的位移为0.5m,则正确的是( )
A.第3s内的平均速度为2.5s未的瞬时速度 B.加速度大小为3.75m/s2
C.加速度大小为4m/s2 D.无法确定加速度大小
4.现在的物理学中加速度的定义式为,而历史上有些科学家曾把相等位移内速度变化相等的单向直线运动称为“匀变速直线运动”(现称“另类匀变速直线运动”),“另类加速度”的定义式为,其中v0、vs分别表示某段位移s内的初速度和末速度。A>0表示物体在做加速运动,A<0表示物体在做减速运动。则下列说法正确的( )
A.若A不变,则a也不变
B.若A>0且保持不变,则a逐渐变大
C.若A不变,则物体在位移中点处的速度比大
D.若A>0且保持不变,则物体在中间时刻的速度比大
5.在足够高的塔顶上以v0= 20m/s的初速度竖直上抛一个小球(不计空气阻力,g = 10m/s2),从抛出至位移大小为15m这段时间内,小球( )
A.平均速度可能为7.5m/s,方向竖直向上
B.平均速率可能为11m/s
C.通过的路程可能为55m
D.平均速度可能为2m/s,方向竖直向下
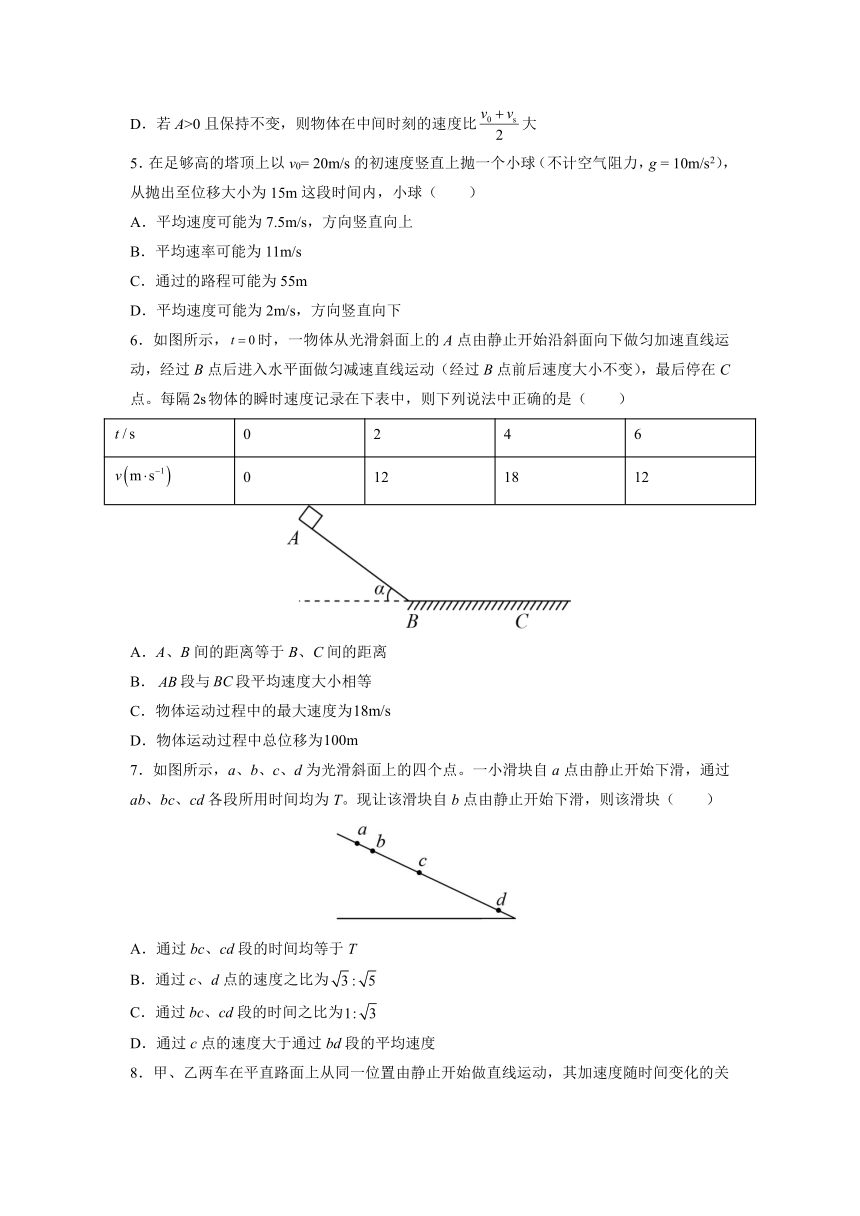
6.如图所示,时,一物体从光滑斜面上的A点由静止开始沿斜面向下做匀加速直线运动,经过B点后进入水平面做匀减速直线运动(经过B点前后速度大小不变),最后停在C点。每隔物体的瞬时速度记录在下表中,则下列说法中正确的是( )
0 2 4 6
0 12 18 12
A.A、B间的距离等于B、C间的距离
B.段与段平均速度大小相等
C.物体运动过程中的最大速度为
D.物体运动过程中总位移为
7.如图所示,a、b、c、d为光滑斜面上的四个点。一小滑块自a点由静止开始下滑,通过ab、bc、cd各段所用时间均为T。现让该滑块自b点由静止开始下滑,则该滑块( )
A.通过bc、cd段的时间均等于T
B.通过c、d点的速度之比为
C.通过bc、cd段的时间之比为
D.通过c点的速度大于通过bd段的平均速度
8.甲、乙两车在平直路面上从同一位置由静止开始做直线运动,其加速度随时间变化的关系如图所示。在时间内,下列说法正确的是( )
A.0-4t0,甲先加速后减速 B.t=2t0时甲、乙速度相等
C.t=2t0时,甲、乙相遇 D.0~t0,甲的位移为
二、多选题。本大题共4小题,每小题5分,共20分,每小题有两项或以上符合题意。
9.某探究小组在调研某款汽车的性能时,记录了该汽车某次沿平直公路由静止启动、匀速行驶和制动停止三个过程的部分数据如表格所示。若汽车启动和制动过程均可视为匀变速直线运动,则在本次测试中,下列说法正确的是( )
时间() 0 2 4 6 8 10 12 14 16 18 20
速度( ) 0 6 12 18 24 30 33 33 24 12 0
A.汽车加速运动的时间为
B.汽车制动过程中加速度的大小为
C.汽车在最后内、最后内的位移之比为
D.汽车通过前、前、前所用时间之比为
10.如图所示,光滑斜面被分成四个相等的部分,一物体从A点以某一初速度沿斜面向上滑动,到达点速度恰好为零,关于物体向上滑动过程中下列结论正确的是( )
A.物体到达、点的速率之比
B.物体到达、经历的时间之比
C.物体通过每一部分时,其速度变化量相等
D.物体从A到E的平均速度等于过点时的瞬时速度
11.质点做匀加速直线运动的初速度为,加速度大小为,经过时间后未速度为v,经测量发现:物体运动到中间位置通过的距离,比物体运动一半时间通过的距离多了9m、且时间差为1s,根据以上条件可以求以下物理量,其中正确的是( )
A.可求得质点的末速度v大小为 B.可求得质点的加速度为为
C.可求得质点的运动时间为6s D.此题条件不足无法求出质点的加速度
12.新冠疫情让2020届高三学生少了很多在校学习的时间,返校后为节约时间,小尧同学都是跑步去排队吃饭。跑步过程中的图象如图所示,为一条不过坐标原点的直线,假定从小尧的教室门口到食堂的道路为一水平直线道路,以教室门口为坐标原点,教室到食堂方向为x轴正方向,下列说法正确的是( )
A.小尧运动到x1的时间为
B.小尧运动到x1的时间为
C.小尧运动的速度与位移成线性规律变化
D.小尧运动的速度随位移的增加而减小,但不成线性规律
三、解答题。本大题共4小题,共40分,解答过程必修有必要的文字说明,公式和解题过程。
13.某同学做“测匀变速直线运动的加速度”的实验装置如图1所示,一小车放在水平长木板上,左侧栓有一细软线,跨过固定在木板边缘的滑轮与一重物相连,小车右侧与穿过电火花计时器的纸带相连,在重物牵引下,小车在木板上向左运动。如图2给出了电火花计时器在纸带上打出的一些计数点,相邻的两个计数点间还有4个点没画出,电火花计时器所用的交流电频率为。
(1)该同学进行了以下实验操作步骤,其中错误的步骤是____________。
A.将打点计时器固定在长木板有滑轮一端,并接好电路
B.将纸带固定在小车尾部,并穿过打点计时器的限位孔
C.把一条细绳拴在小车上,细绳跨过定滑轮,下面吊着适当重的钩码
D.拉住纸带,将小车移到靠近打点计时器的一端后,放开纸带,再接通电源
(2)根据纸带可以计算各点的瞬时速度,现计算第2点的瞬时速度:________(取三位有效数字)
(3)求出小车的加速度为_____(结果取三位有效数字)
(4)如果当时电网中交变电流的频率是,而做实验的同学并不知道,那么加速度的测量值与实际值相比____________(填“偏大”“偏小”或“不变")。
14.如图所示,平直公路上停靠着一辆长的客车,另一车道上的货车以的速度沿公路匀速行驶,货车长。当货车的车尾刚好与客车的车头平齐时,客车以的加速度由静止开始做匀加速直线运动,直到速度达到后保持匀速行驶。客车启动后,求:
(1)追上货车前,客车车头离货车车尾的最远距离;
(2)客车车头与货车车头平齐时,客车的速度大小;
(3)客车自开始运动直到刚好超过货车时的总时间;
(4)若客车刚好超过货车时,客车立即以大小为的加速度做匀减速直线运动至停止,同时货车以大小为的加速度做匀加速直线运动,直到达到的速度后匀速行驶,求客车刚好超过货车后,再经多长时间两车车头再次平齐(结果可保留根号)。
15.在笔直的公路上,一辆以5的速度匀速行驶的小轿车,正要以2的加速度开始加速时,一辆卡车刚好从旁边以25的速度匀速同向驶过,如图所示。已知该路段小轿车最大速度为33,不考虑两车的长度。求:
(1)小轿车追上卡车前,二者之间的最大距离;
(2)小轿车追上卡车所用时间;
(3)当小轿车超过卡车200m时,因突发情况,小轿车立即以3的加速度开始减速,此后卡车再次追上小轿车需要多少时间。
16.据报道,一儿童玩耍时不慎从高的阳台上无初速掉下,在他刚掉下时恰被楼下的管理人员发现,该人员迅速由静止冲向儿童下落处的正下方楼底,准备接住儿童。已知管理人员到楼底的距离为,为确保安全稳妥的接住儿童,管理人员将尽力节约时间,但又必须保证接儿童时没有水平方向的冲击,不计空气阻力,将儿童和管理人员都看做质点,设管理人员奔跑过程中只做匀速或匀变速运动,取。
(1)管理人员至少要用多大的平均速度跑到楼底?
(2)若管理人员在加速或减速过程中的加速度大小相等,且最大速度不超过,求管理人员奔跑时加速度需满足什么条件?
参考答案
1.D
【解析】A.她下落到刚接触网面时的速度为
A错误;
B.她自最高点向下运动到最低点的过程历时
B错误;
C.弹起的速度为
她与网作用过程中的平均加速度为
C错误;
D.下落时间为
她自静止下落到弹回至最高点的过程中,平均速度为
D正确。
故选D。
2.B
【解析】国旗在上升的过程中,若将全程看为匀速,则速度约为,若全程先匀加速到最大值再立即匀减速到0,则最大速度约为,由以上分析可知匀速运动的速度取值介于和之间,故选B。
3.C
【解析】A.根据位移时间公式得,第1的位移为
若第3s末物体仍然没有停止或恰好停止,则第3s内的位移为
代入数据解得
,
第3s的末速度为
说明在3s前物体已经停止,假设不成立。本运动过程可逆向看作初速度为0的匀加速运动,设运动总时间为t,则有:
解得
,
根据平均速度等于中间时刻的瞬时速度,若3s时没停下,第3s内的平均速度为2.5s未的瞬时速度,但已提前停下,故A错误;
BCD.物体的加速度大小为4m/s2,故BD错误,C正确。
故选C。
4.B
【解析】AB.若A不变,有两种情况:当时,相等位移内速度增加量相等,通过相等位移所用的时间越来越短,由可知,a越来越大;当时,相等位移内速度减少量相等,通过相等位移所用的时间越来越多,由可知,a越来越小,故A错误,B正确;
C.当A不变时,相等位移内速度变化量相等,设位移中点处的速度为,则有
可得
故C错误;
D.若且保持不变,则前一半时间内的平均速度小于后一半时间内的平均速度,后一半时间内物体将经过更多的位移,所以物体在中间时刻时,还没有到达中间位置,所以物体在中间时刻的速度比小,故D错误。
故选B。
5.C
【解析】BC.当位移方向向上时,即位移
路程可能为
,
设用时为t,由位移公式得
代入得
解得
当位移方向向下时,即
路程
设用时为,由位移公式得
代入得
解得
(另一值不合理舍去)
根据平均速率
可得:平均速率可能为
B错误,C正确;
AD.平均速度可能为
,
方向竖直向上
方向竖直向下,AD错误。
故选C。
6.B
【解析】C.物体做加速运动时的加速度为
物体做减速运动时的加速度为
设物体做加速运动的时间为t,则有
6s末的速度为
解得
,
物体运动过程中的最大速度为,所以C错误;
A.A、B间的距离为
B、C间的距离为
所以A、B间的距离不等于B、C间的距离,则A错误;
B.段与段平均速度大小为
所以B正确;
D.物体运动过程中总路程为
但是总位移比总路程小,所以D错误;
故选B。
7.D
【解析】A.由题意知,滑块从a点静止下滑,经过各段的时间都是T,所以ab、bc、cd各段的长度之比为1:3:5,则bc、cd段的位移之比为3:5,如果从b点开始静止下滑,则bc间距离大于ab间距离,所以通过bc、cd段的时间均大于T,选项A错误;
B.设bc间距离为3x,则cd间的距离为5x,所以bd间的距离为8x,滑块下滑的加速度为a,滑块从b点开始静止下滑,所以通过c点的速度为
通过d点的速度为
通过c、d点的速度之比为,选项B错误;
C.滑块从b点开始静止下滑,通过bc的时间
通过cd段的时间
通过bc、cd段的时间之比为,选项C错误;
D.对匀变速直线运动来说,平均速度等于中间时刻的瞬时速度,对初速度为零的匀加速直线运动来说,连续相等时间内的位移之比为1:3,所以滑块经过bc的时间大于从b到d时间的二分之一,故通过c点的速度大于bd段的平均速度,选项D正确。
故选D。
8.B
【解析】A.由图可知,甲的加速度一直为正,则甲一直加速,故A错误;
BC.图像与坐标轴围城的面积表示速度变化量的大小,由图可得,在t=2t0甲的速度为
乙的速度为
此时甲、乙速度相同,位移并不相同。故B正确C错误;
D. t=t0时甲的速度为
如果甲做匀加速直线运动,0~t0,时间内甲的位移为,而甲做加速度增大的加速运动。故D错误。
故选B。
9.BD
【解析】A.由题表数据可知,汽车的最大速度为
汽车加速运动时的加速度大小为
所以汽车加速运动的时间为
故A错误;
B.汽车制动过程中加速度的大小为
故B正确;
C.汽车的制动时间为
制动距离为
则汽车在最后内的位移为
将汽车的制动过程逆向看作是反向的初速为零的的匀加速运动,则汽车在最后内的位移为
所以
故C错误;
D.汽车加速过程的位移大小为
根据
可知汽车通过前、前、前所用时间之比为
故D正确。
故选BD。
10.ABD
【解析】将物体从A到E的匀减速直线运动逆向看作是初速度为零的匀加速直线运动,设四个相等部分的长度均为d,则
A.根据
可得物体到达、点的速率之比为
故A正确;
B.根据
可得物体到达、经历的时间之比为
故B正确;
C.根据
可得物体通过每一部分的时间之比为
根据
可知物体通过每一部分时,其速度变化量不相等,故C错误;
D.物体通过A点时的速度为
物体从A到E的平均速度为
物体通过D点时的瞬时速度为
故D正确。
故选ABD。
11.ABC
【解析】AC.根据平均速度推论可知,全程位移可表示为
则前半程位移为
前一半时间内的位移为
由题意可得
即
根据匀变速直线运动的推论可知,中间位置的瞬时速度为
对于后半程有
则后半程的运动时间为
由题意可得
联立代入数据解得
,
AC正确;
BD.加速度为
B正确,D错误。
故选ABC。
12.BD
【解析】AB.由运动学公式
可知,图象与坐标轴所围成的面积等于运动的时间,即
CD.图象的斜率为定值,即
所以
可知,运动的速度与位移不成线性关系,且速度随着位移的增加而减小,C错误,D正确。
故选BD。
13.AD 0.396 0.380 偏大
【解析】(1)[1]A.将打点计时器固定在没有滑轮的一端,故A错误;
B.纸带固定在小车尾部目的是保证和小车具有相同的运动状态,穿过限位孔可以防止纸带歪斜,故B正确;
C.把细绳拴在小车上,细绳跨过定滑轮,下面吊着适当钩码可以带动小车做加速运动,故C正确;
D.实验时,应先接通电源,后释放纸带,故D错误;
(2)[2]根据匀变速直线运动中,某一段时间内的平均速度等于这一段中间时刻的瞬时速度,可知打下计数点2的瞬时速度为
(3)[3]根据逐差法可知滑块的加速度为
(4)[4]如果在某次实验中,交流电的频率49Hz,f<50Hz,那么实际打点周期变大,而计算时仍用T=0.02s计算,根据运动学公式
得真实的加速度值就会偏小,所以测量的加速度值与真实的加速度值相比是偏大。
14.(1);(2);(3);(4)
【解析】(1)由题意可知,当两车速度相同时相距最远,可得
解得两车相距最远的时间为
该段时间内,货车的位移为
客车的位移为
故客车车头离前方货车车尾的最远距离为
(2)设客车自启动到两车车头平齐的时间为,若该过程中客车一直做匀加速直线运动,则满足
解得
,(舍去)
此时客车的速度为
可知两车头平齐前客车已匀速,故客车车头与货车车头平齐时,客车的速度为。
(3)客车加速的时间为
在客车加速的过程中,货车的位移为
客车的位移为
由两车位置关系可知,此时客车车头恰好再次与货车车尾平齐。设自此时到客车刚好超过货车时的时间为,由位移关系可得
解得
故客车自开始运动直到刚好超过货车时的总时间
(4)由题意可知,客车停下的时间为
客车刹车的位移大小为
货车加速后的速度大小为
故该过程中货车做匀加速直线运动,其位移大小为
此时两车头相距
即在客车停下来后两车车头才能平齐,也即到两车头平齐的过程中,货车加速的位移为
由
解得
或(舍去)
此时货车的速度大小为
解得
即客车刚好超过货车后,再经两车车头再次平齐。
15.(1)100m;(2);(3)
【解析】(1)小轿车与卡车速度相等时,二者相距最远
解得
小轿车前进的位移
卡车前进的位移
二者之间的最大距离
(2)当小轿车从开始加速到最大速度时,需要用时
小轿车前进的位移
卡车前进的位移
由于,此时并没追上卡车,设又经历时间小轿车追上卡车,位移满足
解得
小轿车追上卡车所用总时间
(3)小轿车减速到零需要的时间
这段时间内,小轿车刹车位移
卡车前进的位移
由于
此时卡车还没追上小轿车,但小轿车以后静止不动
此时二者相距
设又经历时间卡车追上小轿车,有
卡车再次追上小汽车所需时间
16.(1)6m/s;(2)
【解析】(1)儿童下落的时间为
管理人员平均速度的最小值为
(2)假设管理人员跑至儿童落地点的过程中不存在匀速运动过程,在这种情况下管理人员先匀加速1.5s再匀减速1.5s,使得到达儿童落地点时速度恰好减为零,此时对应的加速度最小,设此过程的最大速度为v0,则
解得
假设不成立,所以管理人员先以最小加速度加速至最大速度vm后匀速运动一段时间后,再匀减速运动,到达儿童落地点时速度恰好减为零,设管理人员匀加速和匀减速的时间均为t0,则
解得
所以管理人员的加速度最小值为
即理人员奔跑时加速度应满足的条件为
一、单选题。本大题共8小题,每小题5分,共40分,每小题只有一个选项符合题意。
1.蹦床是一项专业运动员利用蹦床的反弹效果表现技巧的竞技运动,属体操项目之一。朱雪莹在东京奥运会夺冠一跳如图所示。某段过程中,她自距水平网面高3.2m处由静止下落,与网作用0.5s后,竖直向上弹离水平网面的最大高度为5m,若忽略触网过程中蹬网发力动作而将其视为质点,不计空气阻力且规定竖直向下为正方向, 。下列说法正确的是( )
A.她下落到刚接触网面时的速度为10m/s
B.她自最高点向下运动到最低点的过程历时0.8s
C.她与网作用过程中的平均加速度为-4m/s2
D.她自静止下落到弹回至最高点的过程中,平均速度为
2.2021年10月1日,新中国迎来72周年华诞.天安门广场鲜艳的五星红旗冉冉升起!升旗手要在两分零七秒的时间内分秒不差的将国旗从旗杆底升到杆顶。现将升旗过程简化为:先做初速度为零的匀加速运动,再做匀速运动,最后匀减速运动到零。已知国旗上升的高度为28.3m,国旗在匀速阶段的速度可能为( )
A.0.20m/s B.0.30m/s C.0.50m/s D.0.60m/s
3.一物体在摩擦力作用下在水平地面上匀减速滑动,若已知物体在第1s内的位移为8m,在第3内的位移为0.5m,则正确的是( )
A.第3s内的平均速度为2.5s未的瞬时速度 B.加速度大小为3.75m/s2
C.加速度大小为4m/s2 D.无法确定加速度大小
4.现在的物理学中加速度的定义式为,而历史上有些科学家曾把相等位移内速度变化相等的单向直线运动称为“匀变速直线运动”(现称“另类匀变速直线运动”),“另类加速度”的定义式为,其中v0、vs分别表示某段位移s内的初速度和末速度。A>0表示物体在做加速运动,A<0表示物体在做减速运动。则下列说法正确的( )
A.若A不变,则a也不变
B.若A>0且保持不变,则a逐渐变大
C.若A不变,则物体在位移中点处的速度比大
D.若A>0且保持不变,则物体在中间时刻的速度比大
5.在足够高的塔顶上以v0= 20m/s的初速度竖直上抛一个小球(不计空气阻力,g = 10m/s2),从抛出至位移大小为15m这段时间内,小球( )
A.平均速度可能为7.5m/s,方向竖直向上
B.平均速率可能为11m/s
C.通过的路程可能为55m
D.平均速度可能为2m/s,方向竖直向下
6.如图所示,时,一物体从光滑斜面上的A点由静止开始沿斜面向下做匀加速直线运动,经过B点后进入水平面做匀减速直线运动(经过B点前后速度大小不变),最后停在C点。每隔物体的瞬时速度记录在下表中,则下列说法中正确的是( )
0 2 4 6
0 12 18 12
A.A、B间的距离等于B、C间的距离
B.段与段平均速度大小相等
C.物体运动过程中的最大速度为
D.物体运动过程中总位移为
7.如图所示,a、b、c、d为光滑斜面上的四个点。一小滑块自a点由静止开始下滑,通过ab、bc、cd各段所用时间均为T。现让该滑块自b点由静止开始下滑,则该滑块( )
A.通过bc、cd段的时间均等于T
B.通过c、d点的速度之比为
C.通过bc、cd段的时间之比为
D.通过c点的速度大于通过bd段的平均速度
8.甲、乙两车在平直路面上从同一位置由静止开始做直线运动,其加速度随时间变化的关系如图所示。在时间内,下列说法正确的是( )
A.0-4t0,甲先加速后减速 B.t=2t0时甲、乙速度相等
C.t=2t0时,甲、乙相遇 D.0~t0,甲的位移为
二、多选题。本大题共4小题,每小题5分,共20分,每小题有两项或以上符合题意。
9.某探究小组在调研某款汽车的性能时,记录了该汽车某次沿平直公路由静止启动、匀速行驶和制动停止三个过程的部分数据如表格所示。若汽车启动和制动过程均可视为匀变速直线运动,则在本次测试中,下列说法正确的是( )
时间() 0 2 4 6 8 10 12 14 16 18 20
速度( ) 0 6 12 18 24 30 33 33 24 12 0
A.汽车加速运动的时间为
B.汽车制动过程中加速度的大小为
C.汽车在最后内、最后内的位移之比为
D.汽车通过前、前、前所用时间之比为
10.如图所示,光滑斜面被分成四个相等的部分,一物体从A点以某一初速度沿斜面向上滑动,到达点速度恰好为零,关于物体向上滑动过程中下列结论正确的是( )
A.物体到达、点的速率之比
B.物体到达、经历的时间之比
C.物体通过每一部分时,其速度变化量相等
D.物体从A到E的平均速度等于过点时的瞬时速度
11.质点做匀加速直线运动的初速度为,加速度大小为,经过时间后未速度为v,经测量发现:物体运动到中间位置通过的距离,比物体运动一半时间通过的距离多了9m、且时间差为1s,根据以上条件可以求以下物理量,其中正确的是( )
A.可求得质点的末速度v大小为 B.可求得质点的加速度为为
C.可求得质点的运动时间为6s D.此题条件不足无法求出质点的加速度
12.新冠疫情让2020届高三学生少了很多在校学习的时间,返校后为节约时间,小尧同学都是跑步去排队吃饭。跑步过程中的图象如图所示,为一条不过坐标原点的直线,假定从小尧的教室门口到食堂的道路为一水平直线道路,以教室门口为坐标原点,教室到食堂方向为x轴正方向,下列说法正确的是( )
A.小尧运动到x1的时间为
B.小尧运动到x1的时间为
C.小尧运动的速度与位移成线性规律变化
D.小尧运动的速度随位移的增加而减小,但不成线性规律
三、解答题。本大题共4小题,共40分,解答过程必修有必要的文字说明,公式和解题过程。
13.某同学做“测匀变速直线运动的加速度”的实验装置如图1所示,一小车放在水平长木板上,左侧栓有一细软线,跨过固定在木板边缘的滑轮与一重物相连,小车右侧与穿过电火花计时器的纸带相连,在重物牵引下,小车在木板上向左运动。如图2给出了电火花计时器在纸带上打出的一些计数点,相邻的两个计数点间还有4个点没画出,电火花计时器所用的交流电频率为。
(1)该同学进行了以下实验操作步骤,其中错误的步骤是____________。
A.将打点计时器固定在长木板有滑轮一端,并接好电路
B.将纸带固定在小车尾部,并穿过打点计时器的限位孔
C.把一条细绳拴在小车上,细绳跨过定滑轮,下面吊着适当重的钩码
D.拉住纸带,将小车移到靠近打点计时器的一端后,放开纸带,再接通电源
(2)根据纸带可以计算各点的瞬时速度,现计算第2点的瞬时速度:________(取三位有效数字)
(3)求出小车的加速度为_____(结果取三位有效数字)
(4)如果当时电网中交变电流的频率是,而做实验的同学并不知道,那么加速度的测量值与实际值相比____________(填“偏大”“偏小”或“不变")。
14.如图所示,平直公路上停靠着一辆长的客车,另一车道上的货车以的速度沿公路匀速行驶,货车长。当货车的车尾刚好与客车的车头平齐时,客车以的加速度由静止开始做匀加速直线运动,直到速度达到后保持匀速行驶。客车启动后,求:
(1)追上货车前,客车车头离货车车尾的最远距离;
(2)客车车头与货车车头平齐时,客车的速度大小;
(3)客车自开始运动直到刚好超过货车时的总时间;
(4)若客车刚好超过货车时,客车立即以大小为的加速度做匀减速直线运动至停止,同时货车以大小为的加速度做匀加速直线运动,直到达到的速度后匀速行驶,求客车刚好超过货车后,再经多长时间两车车头再次平齐(结果可保留根号)。
15.在笔直的公路上,一辆以5的速度匀速行驶的小轿车,正要以2的加速度开始加速时,一辆卡车刚好从旁边以25的速度匀速同向驶过,如图所示。已知该路段小轿车最大速度为33,不考虑两车的长度。求:
(1)小轿车追上卡车前,二者之间的最大距离;
(2)小轿车追上卡车所用时间;
(3)当小轿车超过卡车200m时,因突发情况,小轿车立即以3的加速度开始减速,此后卡车再次追上小轿车需要多少时间。
16.据报道,一儿童玩耍时不慎从高的阳台上无初速掉下,在他刚掉下时恰被楼下的管理人员发现,该人员迅速由静止冲向儿童下落处的正下方楼底,准备接住儿童。已知管理人员到楼底的距离为,为确保安全稳妥的接住儿童,管理人员将尽力节约时间,但又必须保证接儿童时没有水平方向的冲击,不计空气阻力,将儿童和管理人员都看做质点,设管理人员奔跑过程中只做匀速或匀变速运动,取。
(1)管理人员至少要用多大的平均速度跑到楼底?
(2)若管理人员在加速或减速过程中的加速度大小相等,且最大速度不超过,求管理人员奔跑时加速度需满足什么条件?
参考答案
1.D
【解析】A.她下落到刚接触网面时的速度为
A错误;
B.她自最高点向下运动到最低点的过程历时
B错误;
C.弹起的速度为
她与网作用过程中的平均加速度为
C错误;
D.下落时间为
她自静止下落到弹回至最高点的过程中,平均速度为
D正确。
故选D。
2.B
【解析】国旗在上升的过程中,若将全程看为匀速,则速度约为,若全程先匀加速到最大值再立即匀减速到0,则最大速度约为,由以上分析可知匀速运动的速度取值介于和之间,故选B。
3.C
【解析】A.根据位移时间公式得,第1的位移为
若第3s末物体仍然没有停止或恰好停止,则第3s内的位移为
代入数据解得
,
第3s的末速度为
说明在3s前物体已经停止,假设不成立。本运动过程可逆向看作初速度为0的匀加速运动,设运动总时间为t,则有:
解得
,
根据平均速度等于中间时刻的瞬时速度,若3s时没停下,第3s内的平均速度为2.5s未的瞬时速度,但已提前停下,故A错误;
BCD.物体的加速度大小为4m/s2,故BD错误,C正确。
故选C。
4.B
【解析】AB.若A不变,有两种情况:当时,相等位移内速度增加量相等,通过相等位移所用的时间越来越短,由可知,a越来越大;当时,相等位移内速度减少量相等,通过相等位移所用的时间越来越多,由可知,a越来越小,故A错误,B正确;
C.当A不变时,相等位移内速度变化量相等,设位移中点处的速度为,则有
可得
故C错误;
D.若且保持不变,则前一半时间内的平均速度小于后一半时间内的平均速度,后一半时间内物体将经过更多的位移,所以物体在中间时刻时,还没有到达中间位置,所以物体在中间时刻的速度比小,故D错误。
故选B。
5.C
【解析】BC.当位移方向向上时,即位移
路程可能为
,
设用时为t,由位移公式得
代入得
解得
当位移方向向下时,即
路程
设用时为,由位移公式得
代入得
解得
(另一值不合理舍去)
根据平均速率
可得:平均速率可能为
B错误,C正确;
AD.平均速度可能为
,
方向竖直向上
方向竖直向下,AD错误。
故选C。
6.B
【解析】C.物体做加速运动时的加速度为
物体做减速运动时的加速度为
设物体做加速运动的时间为t,则有
6s末的速度为
解得
,
物体运动过程中的最大速度为,所以C错误;
A.A、B间的距离为
B、C间的距离为
所以A、B间的距离不等于B、C间的距离,则A错误;
B.段与段平均速度大小为
所以B正确;
D.物体运动过程中总路程为
但是总位移比总路程小,所以D错误;
故选B。
7.D
【解析】A.由题意知,滑块从a点静止下滑,经过各段的时间都是T,所以ab、bc、cd各段的长度之比为1:3:5,则bc、cd段的位移之比为3:5,如果从b点开始静止下滑,则bc间距离大于ab间距离,所以通过bc、cd段的时间均大于T,选项A错误;
B.设bc间距离为3x,则cd间的距离为5x,所以bd间的距离为8x,滑块下滑的加速度为a,滑块从b点开始静止下滑,所以通过c点的速度为
通过d点的速度为
通过c、d点的速度之比为,选项B错误;
C.滑块从b点开始静止下滑,通过bc的时间
通过cd段的时间
通过bc、cd段的时间之比为,选项C错误;
D.对匀变速直线运动来说,平均速度等于中间时刻的瞬时速度,对初速度为零的匀加速直线运动来说,连续相等时间内的位移之比为1:3,所以滑块经过bc的时间大于从b到d时间的二分之一,故通过c点的速度大于bd段的平均速度,选项D正确。
故选D。
8.B
【解析】A.由图可知,甲的加速度一直为正,则甲一直加速,故A错误;
BC.图像与坐标轴围城的面积表示速度变化量的大小,由图可得,在t=2t0甲的速度为
乙的速度为
此时甲、乙速度相同,位移并不相同。故B正确C错误;
D. t=t0时甲的速度为
如果甲做匀加速直线运动,0~t0,时间内甲的位移为,而甲做加速度增大的加速运动。故D错误。
故选B。
9.BD
【解析】A.由题表数据可知,汽车的最大速度为
汽车加速运动时的加速度大小为
所以汽车加速运动的时间为
故A错误;
B.汽车制动过程中加速度的大小为
故B正确;
C.汽车的制动时间为
制动距离为
则汽车在最后内的位移为
将汽车的制动过程逆向看作是反向的初速为零的的匀加速运动,则汽车在最后内的位移为
所以
故C错误;
D.汽车加速过程的位移大小为
根据
可知汽车通过前、前、前所用时间之比为
故D正确。
故选BD。
10.ABD
【解析】将物体从A到E的匀减速直线运动逆向看作是初速度为零的匀加速直线运动,设四个相等部分的长度均为d,则
A.根据
可得物体到达、点的速率之比为
故A正确;
B.根据
可得物体到达、经历的时间之比为
故B正确;
C.根据
可得物体通过每一部分的时间之比为
根据
可知物体通过每一部分时,其速度变化量不相等,故C错误;
D.物体通过A点时的速度为
物体从A到E的平均速度为
物体通过D点时的瞬时速度为
故D正确。
故选ABD。
11.ABC
【解析】AC.根据平均速度推论可知,全程位移可表示为
则前半程位移为
前一半时间内的位移为
由题意可得
即
根据匀变速直线运动的推论可知,中间位置的瞬时速度为
对于后半程有
则后半程的运动时间为
由题意可得
联立代入数据解得
,
AC正确;
BD.加速度为
B正确,D错误。
故选ABC。
12.BD
【解析】AB.由运动学公式
可知,图象与坐标轴所围成的面积等于运动的时间,即
CD.图象的斜率为定值,即
所以
可知,运动的速度与位移不成线性关系,且速度随着位移的增加而减小,C错误,D正确。
故选BD。
13.AD 0.396 0.380 偏大
【解析】(1)[1]A.将打点计时器固定在没有滑轮的一端,故A错误;
B.纸带固定在小车尾部目的是保证和小车具有相同的运动状态,穿过限位孔可以防止纸带歪斜,故B正确;
C.把细绳拴在小车上,细绳跨过定滑轮,下面吊着适当钩码可以带动小车做加速运动,故C正确;
D.实验时,应先接通电源,后释放纸带,故D错误;
(2)[2]根据匀变速直线运动中,某一段时间内的平均速度等于这一段中间时刻的瞬时速度,可知打下计数点2的瞬时速度为
(3)[3]根据逐差法可知滑块的加速度为
(4)[4]如果在某次实验中,交流电的频率49Hz,f<50Hz,那么实际打点周期变大,而计算时仍用T=0.02s计算,根据运动学公式
得真实的加速度值就会偏小,所以测量的加速度值与真实的加速度值相比是偏大。
14.(1);(2);(3);(4)
【解析】(1)由题意可知,当两车速度相同时相距最远,可得
解得两车相距最远的时间为
该段时间内,货车的位移为
客车的位移为
故客车车头离前方货车车尾的最远距离为
(2)设客车自启动到两车车头平齐的时间为,若该过程中客车一直做匀加速直线运动,则满足
解得
,(舍去)
此时客车的速度为
可知两车头平齐前客车已匀速,故客车车头与货车车头平齐时,客车的速度为。
(3)客车加速的时间为
在客车加速的过程中,货车的位移为
客车的位移为
由两车位置关系可知,此时客车车头恰好再次与货车车尾平齐。设自此时到客车刚好超过货车时的时间为,由位移关系可得
解得
故客车自开始运动直到刚好超过货车时的总时间
(4)由题意可知,客车停下的时间为
客车刹车的位移大小为
货车加速后的速度大小为
故该过程中货车做匀加速直线运动,其位移大小为
此时两车头相距
即在客车停下来后两车车头才能平齐,也即到两车头平齐的过程中,货车加速的位移为
由
解得
或(舍去)
此时货车的速度大小为
解得
即客车刚好超过货车后,再经两车车头再次平齐。
15.(1)100m;(2);(3)
【解析】(1)小轿车与卡车速度相等时,二者相距最远
解得
小轿车前进的位移
卡车前进的位移
二者之间的最大距离
(2)当小轿车从开始加速到最大速度时,需要用时
小轿车前进的位移
卡车前进的位移
由于,此时并没追上卡车,设又经历时间小轿车追上卡车,位移满足
解得
小轿车追上卡车所用总时间
(3)小轿车减速到零需要的时间
这段时间内,小轿车刹车位移
卡车前进的位移
由于
此时卡车还没追上小轿车,但小轿车以后静止不动
此时二者相距
设又经历时间卡车追上小轿车,有
卡车再次追上小汽车所需时间
16.(1)6m/s;(2)
【解析】(1)儿童下落的时间为
管理人员平均速度的最小值为
(2)假设管理人员跑至儿童落地点的过程中不存在匀速运动过程,在这种情况下管理人员先匀加速1.5s再匀减速1.5s,使得到达儿童落地点时速度恰好减为零,此时对应的加速度最小,设此过程的最大速度为v0,则
解得
假设不成立,所以管理人员先以最小加速度加速至最大速度vm后匀速运动一段时间后,再匀减速运动,到达儿童落地点时速度恰好减为零,设管理人员匀加速和匀减速的时间均为t0,则
解得
所以管理人员的加速度最小值为
即理人员奔跑时加速度应满足的条件为
