山西省运城市2022届高三上学期期中考试数学(文)试题(Word版含答案)
文档属性
| 名称 | 山西省运城市2022届高三上学期期中考试数学(文)试题(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 615.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-21 00:00:00 | ||
图片预览




文档简介
运城市2022届高三上学期期中考试
数学(文)试题
2021.11
本试题满分150分,考试时间120分钟。答案一律写在答题卡上。
注意事项:
1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.答题时使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
4.保持卡面清洁,不折叠,不破损。
5.做选考题时,考生按照题目要求做答,并用2B铅笔在答题卡上把所选题目对应的题目涂黑。
一、选择题(本大题共12小题,每小题5分,满分60分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合,,且,则实数的值为
A. B.1 C. D.3
2.下列函数是偶函数,且在上是增函数的是
A. B.
C. D.
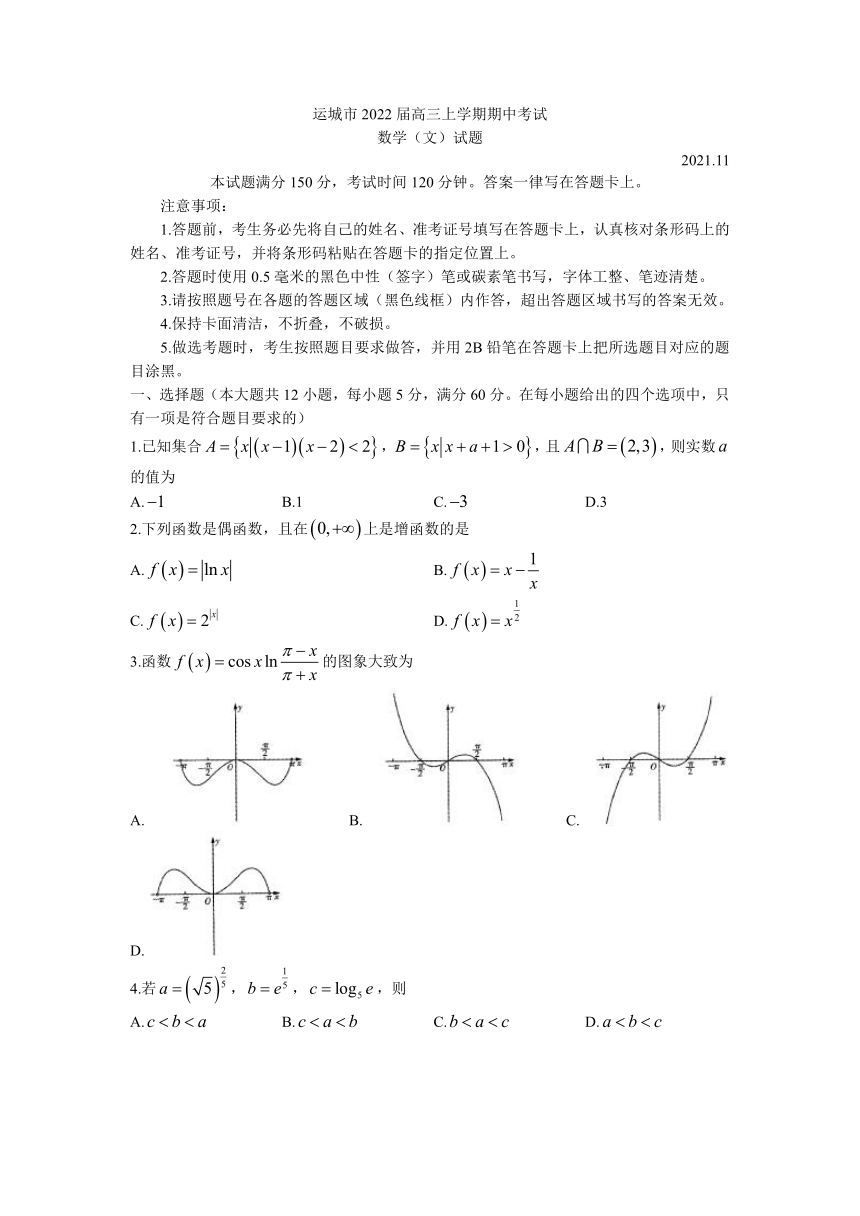
3.函数的图象大致为
A. B. C. D.
4.若,,,则
A. B. C. D.
5.若实数,满足约束条件,则的取值范围是
A. B. C. D.
6.在中,三边上的高的大小依次是,,,则为
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不存在这样的三角形
7.数列中,,,若,则
A.3 B.2 C.5 D.4
8.在正方体中,,,,分别是,,,的中点,则异面直线与所成角的大小是
A. B. C. D.
9.已知,是函数(,)相邻的两个零点,若函数在上的最大值为1,则的取值范围是
A. B. C. D.
10.数列前项和是,且满足,,,则的值为
A. B. C. D.
11.在中,若,则的取值范围为
A. B. C. D.
12.已知定义在上的函数满足,其中是函数的导函数,若,则实数的取值范围是
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.在中,若,,,则向量与的夹角为______.
14.已知角的顶点为坐标原点,始边与轴的非负半轴重合,终边经过点,,且,则______.
15.若正数,满足,则的最小值是______.
16.如图,正四棱锥的每个顶点都在球的球面上,侧面是等边三角形.若半球的球心为四棱锥的底面中心,且半球与四个侧面均相切,则半球的体积与球的体积的比值为______.
三、解答题(共70分。解答应写出文字说明、证明过程或演算步骤)
第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(本小题12分)
已知函数(,,)的图象经过点,当时,取最大值1,当时,取最小值,且的最小值为.
(1)求的解析式;
(2)设,,,,求角的大小.
18.(本小题12分)
下列关于星星的图案构成一个数列,对应图中星星的个数.
(1)写出,的值及数列的通项公式;
(2)求出数列的前项和;
(3)若,对于(2)中的,有,求数列的前项和.
19.(本小题12分)
在中,角、、所对的边分别为,,,已知
(1)求角的大小;
(2)的面积等于,为边的中点,当中线的长最短时,求边长.
20.(本小题12分)
如图,在四棱锥中,四边形是菱形,对角线与的交点为,,,.
(1)证明:平面;
(2)点在棱上,若体积,求①点的位置;②与平面所成角的正切值.
21.(本小题12分)
已知函数,其中是自然对数的底数,.
(1)当时,求正整数的值,使方程在上有解;
(2)若在区间单调递增,求的取值范围.
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
22.【选修4-4:坐标系与参数方程】(10分)
在直角坐标系中,曲线的参数方程为(为参数),以坐标原点为极点,轴正半轴为极轴建立极坐标系,直线的极坐标方程为.
(1)求曲线的普通方程与直线的直角坐标方程;
(2)若直线与曲线交于,两点,点,求的值.
23.【选修4-5:不等式选讲】(10分)已知函数,.
(1)求解不等式的解集;
(2)记的最小值为,若,,且,证明:.
运城市高三文科数学试题答案
一、选择题
1-5 CCCAD 6-10 BDACD 11-12 BD
二、填空题
13. 14. 15. 16.
三、解答题
17.解:(1)依题意有,最大值与最小值间的横坐标最小距离为,则
,,,……………………………………………………2分
则,将点代入得,而,
∴ ∴,………………………………………………4分
故;………………………………………………5分
(2),,………………6分
, ∴,,………………………………8分
∴…………10分
,∴.…………………………………………12分
18.解:(1)知,,;…………………………3分
(2)得,…………………………5分
则;……………………7分
(3),………………………………8分
数列的前项和为…………………………9分
①当时,…………………………10分
②当时,
………………11分
则;…………………………………………12分
19.解:(1)由得………………1分
即………………………………3分
∵,∴,从而………………………………4分
而,所以;……………………………………5分
(2)∵,∴,……………………6分
在中,由余弦定理可得
……………………………………8分
当且仅当时,即当,时,等号成立. ……………………9分
此时,故.…………12分
20.证明:(1)∵,且为中点,∴.……………………1分
在菱形中,∵,,∴,.………………2分
又,∴.∵,∴,
.…………………………4分
∵,∴平面;…………………………5分
(2)①∵,∴,即,
∴,为的中点. ……………………………………7分
②作交与点,连结.
∵,,∴平面,……………………8分
∴平面,是与平面所成的角. ……………………9分
∵,,
.………………………………12分
21.解:(1)当时,方程即为,由于,所以不是方程的解
所以原方程等价于,令,
因为对于恒成立,
所以在内是单调增函数,…………………………4分
又,,
所以方程有且只有1个实数根在区间,
所以整数的值为1. ……………………………………6分
(2),
当时,,在上恒成立,当且仅当时
取等号,故符合要求………………………………7分
当时,令,因为,
所以有两个不相等的实数根,,不妨设,
因此有极大值又有极小值.
若,因为,所以在内有极值点,
故在上不单调. …………………………9分
若,可知,
因为的图象开口向下,要使在上单调,因为,
必须满足即所以.…………………………11分
综上可知,的取值范围是.………………………………12分
22.解:
(Ⅰ),;………………………………5分
(Ⅱ)(为参数),将其代入椭圆方程,有,………………7分
,对应的参数分别为,,有,,………………8分
所以.……………………10分
23.解:(1)
则等价于或或,……………………3分
解得或或.
综上,不等式的解集为;……………………5分
(2)证明:由(1)知,的最小值为3,即,则………………6分
由,,知,,
∴……………………8分
.……………………9分
当且仅当且时等号成立.
∴.………………………………10分
数学(文)试题
2021.11
本试题满分150分,考试时间120分钟。答案一律写在答题卡上。
注意事项:
1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.答题时使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
4.保持卡面清洁,不折叠,不破损。
5.做选考题时,考生按照题目要求做答,并用2B铅笔在答题卡上把所选题目对应的题目涂黑。
一、选择题(本大题共12小题,每小题5分,满分60分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合,,且,则实数的值为
A. B.1 C. D.3
2.下列函数是偶函数,且在上是增函数的是
A. B.
C. D.
3.函数的图象大致为
A. B. C. D.
4.若,,,则
A. B. C. D.
5.若实数,满足约束条件,则的取值范围是
A. B. C. D.
6.在中,三边上的高的大小依次是,,,则为
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不存在这样的三角形
7.数列中,,,若,则
A.3 B.2 C.5 D.4
8.在正方体中,,,,分别是,,,的中点,则异面直线与所成角的大小是
A. B. C. D.
9.已知,是函数(,)相邻的两个零点,若函数在上的最大值为1,则的取值范围是
A. B. C. D.
10.数列前项和是,且满足,,,则的值为
A. B. C. D.
11.在中,若,则的取值范围为
A. B. C. D.
12.已知定义在上的函数满足,其中是函数的导函数,若,则实数的取值范围是
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.在中,若,,,则向量与的夹角为______.
14.已知角的顶点为坐标原点,始边与轴的非负半轴重合,终边经过点,,且,则______.
15.若正数,满足,则的最小值是______.
16.如图,正四棱锥的每个顶点都在球的球面上,侧面是等边三角形.若半球的球心为四棱锥的底面中心,且半球与四个侧面均相切,则半球的体积与球的体积的比值为______.
三、解答题(共70分。解答应写出文字说明、证明过程或演算步骤)
第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(本小题12分)
已知函数(,,)的图象经过点,当时,取最大值1,当时,取最小值,且的最小值为.
(1)求的解析式;
(2)设,,,,求角的大小.
18.(本小题12分)
下列关于星星的图案构成一个数列,对应图中星星的个数.
(1)写出,的值及数列的通项公式;
(2)求出数列的前项和;
(3)若,对于(2)中的,有,求数列的前项和.
19.(本小题12分)
在中,角、、所对的边分别为,,,已知
(1)求角的大小;
(2)的面积等于,为边的中点,当中线的长最短时,求边长.
20.(本小题12分)
如图,在四棱锥中,四边形是菱形,对角线与的交点为,,,.
(1)证明:平面;
(2)点在棱上,若体积,求①点的位置;②与平面所成角的正切值.
21.(本小题12分)
已知函数,其中是自然对数的底数,.
(1)当时,求正整数的值,使方程在上有解;
(2)若在区间单调递增,求的取值范围.
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
22.【选修4-4:坐标系与参数方程】(10分)
在直角坐标系中,曲线的参数方程为(为参数),以坐标原点为极点,轴正半轴为极轴建立极坐标系,直线的极坐标方程为.
(1)求曲线的普通方程与直线的直角坐标方程;
(2)若直线与曲线交于,两点,点,求的值.
23.【选修4-5:不等式选讲】(10分)已知函数,.
(1)求解不等式的解集;
(2)记的最小值为,若,,且,证明:.
运城市高三文科数学试题答案
一、选择题
1-5 CCCAD 6-10 BDACD 11-12 BD
二、填空题
13. 14. 15. 16.
三、解答题
17.解:(1)依题意有,最大值与最小值间的横坐标最小距离为,则
,,,……………………………………………………2分
则,将点代入得,而,
∴ ∴,………………………………………………4分
故;………………………………………………5分
(2),,………………6分
, ∴,,………………………………8分
∴…………10分
,∴.…………………………………………12分
18.解:(1)知,,;…………………………3分
(2)得,…………………………5分
则;……………………7分
(3),………………………………8分
数列的前项和为…………………………9分
①当时,…………………………10分
②当时,
………………11分
则;…………………………………………12分
19.解:(1)由得………………1分
即………………………………3分
∵,∴,从而………………………………4分
而,所以;……………………………………5分
(2)∵,∴,……………………6分
在中,由余弦定理可得
……………………………………8分
当且仅当时,即当,时,等号成立. ……………………9分
此时,故.…………12分
20.证明:(1)∵,且为中点,∴.……………………1分
在菱形中,∵,,∴,.………………2分
又,∴.∵,∴,
.…………………………4分
∵,∴平面;…………………………5分
(2)①∵,∴,即,
∴,为的中点. ……………………………………7分
②作交与点,连结.
∵,,∴平面,……………………8分
∴平面,是与平面所成的角. ……………………9分
∵,,
.………………………………12分
21.解:(1)当时,方程即为,由于,所以不是方程的解
所以原方程等价于,令,
因为对于恒成立,
所以在内是单调增函数,…………………………4分
又,,
所以方程有且只有1个实数根在区间,
所以整数的值为1. ……………………………………6分
(2),
当时,,在上恒成立,当且仅当时
取等号,故符合要求………………………………7分
当时,令,因为,
所以有两个不相等的实数根,,不妨设,
因此有极大值又有极小值.
若,因为,所以在内有极值点,
故在上不单调. …………………………9分
若,可知,
因为的图象开口向下,要使在上单调,因为,
必须满足即所以.…………………………11分
综上可知,的取值范围是.………………………………12分
22.解:
(Ⅰ),;………………………………5分
(Ⅱ)(为参数),将其代入椭圆方程,有,………………7分
,对应的参数分别为,,有,,………………8分
所以.……………………10分
23.解:(1)
则等价于或或,……………………3分
解得或或.
综上,不等式的解集为;……………………5分
(2)证明:由(1)知,的最小值为3,即,则………………6分
由,,知,,
∴……………………8分
.……………………9分
当且仅当且时等号成立.
∴.………………………………10分
同课章节目录
