2021-2022学年沪科版(2012) 七年级数学上第三单元测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版(2012) 七年级数学上第三单元测试题(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 313.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 19:17:27 | ||
图片预览




文档简介
2021-2022学年沪科版(2012) 七年级数学上第三单元测试题
一、单选题(共40分)
1.(本题4分)下列方程中,①;②;③;④,是二元一次方程的有( )
A.1个 B.2个 C.3个 D.4个
2.(本题4分)如果方程与下面方程中的一个组成的方程组的解为,这个方程可以是( )
A. B. C. D.
3.(本题4分)利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式放置,再交换两木块的位置,按图②所示的方式放置.测量的数据如图,则桌子的高度等于( )
A.70cm B.75cm C.80cm D.85cm
4.(本题4分)我国古代数学著作《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五,屈绳量之不足一尺,问木长几何?”大致意思是:“用一根绳子去量一根木条,绳子剩余4.5尺,将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”设绳子长为x尺,木条长为y尺,则根据题意所列方程组正确的是( )
A.B. C. D.
5.(本题4分)已知,则( )
A. B. C. D.
6.(本题4分)早餐店里,小明妈妈买了5个馒头,3个包子,老板少要1元,只要10元;小红爸爸买了8个馒头,6个包子,老板九折优惠,只要18元.若馒头每个x元,包子每个y元,则所列二元一次方程组正确的是( )
A. B. C. D.
7.(本题4分)已知关于,的方程组给出下列结论:
①当时,方程组的解也是的解;
②无论取何值,,的值不可能是互为相反数;
③,都为自然数的解有对.
正确的有几个( )
A. B. C. D.
8.(本题4分)如图1是2021年3月份的月历,小军同学用“”字形框在月历上框出四个数字,将该“”字形框上下左右移动,且一定要框住月历中的四个日期,若四个日期如图2所示,则下列关于,的关系正确的是( )
A. B. C. D.
9.(本题4分)若关于,的二元一次方程组的解也是二元一次方程的解,则的值为( ).
A. B. C. D.
10.(本题4分)甲、乙两人同求方程ax-by=7的整数解,甲正确地求出一个解为,乙把ax-by=7看成ax-by=1,求得一个解为,则a,b的值分别为( )
A. B. C. D.
二、填空题(共20分)
11.(本题5分)二元一次方程的正整数解为________.
12.(本题5分)已知是关于的二元一次方程的一个解,则的值为____.
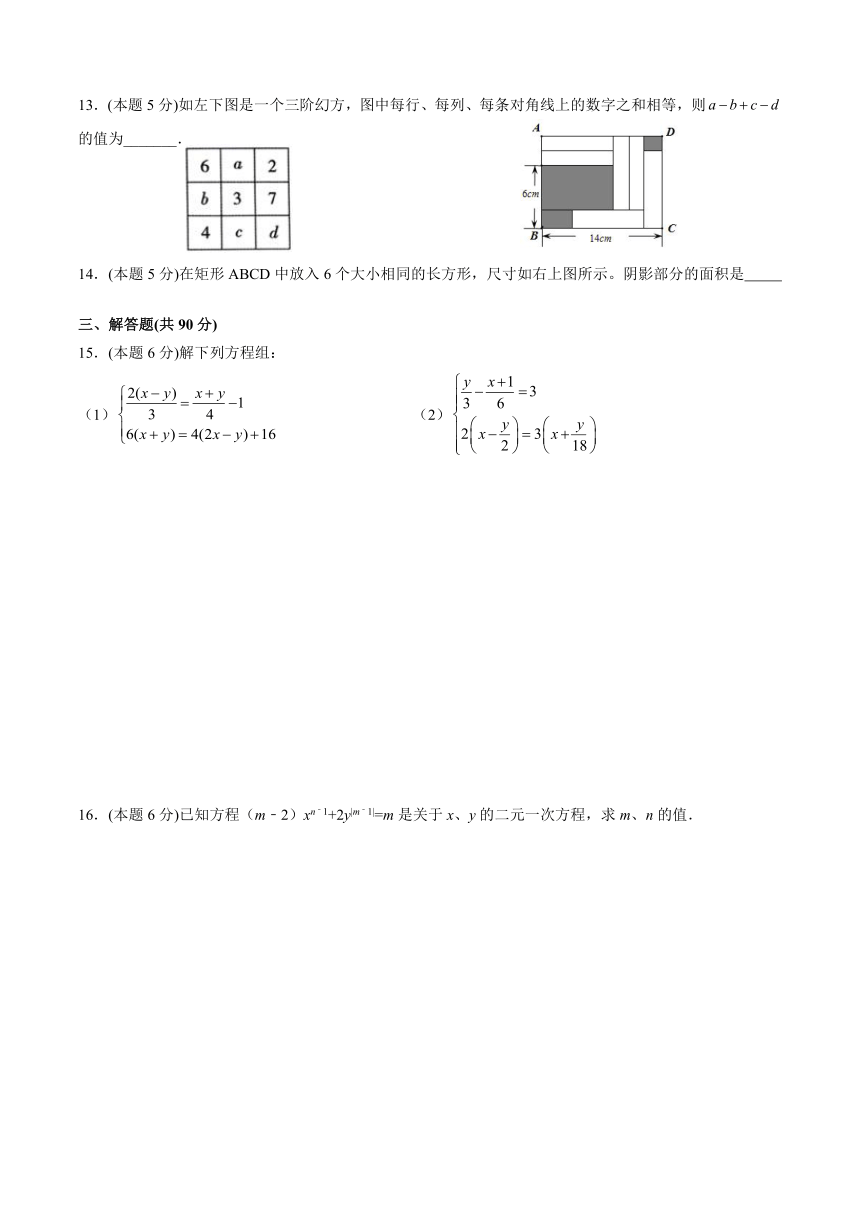
13.(本题5分)如左下图是一个三阶幻方,图中每行、每列、每条对角线上的数字之和相等,则的值为_______.
14.(本题5分)在矩形ABCD中放入6个大小相同的长方形,尺寸如右上图所示。阴影部分的面积是
三、解答题(共90分)
15.(本题6分)解下列方程组:
(1) (2)
16.(本题6分)已知方程(m﹣2)xn﹣1+2y|m﹣1|=m是关于x、y的二元一次方程,求m、n的值.
17.(本题6分)若关于、的二元一次方程组与方程组有相同的解.求、的值.
18.(本题8分)甲、乙两件服装的进价共500元,商店老板将甲种服装按的利润定价,乙种服装按的利润定价,在实际出售时,应顾客要求,两件服装均按九折出售,这样商店老板共获利157元.求甲、乙两件服装的进价各是多少元?
19.(本题8分)已知(x+1)3=ax3+bx2+cx+d,求a+b+c的值.
20.(本题10分)已知等式对于一切有理数都成立,求A,B的值.
21.(本题10分)已知,且5A-2B的值是一个常数.
(1)求的值.
(2)关于x的方程的解与方程3m-2x=1-x的解互为相反数,求m的值.
22.(本题10分)已知,x无论取什么值,式子必为同一定值,求的值.
23.(本题12分)用8个形状和大小都相同的小长方形,恰好可以拼成如图1所示的大长方形;若用这8个小长方形拼成如图2所示的正方形,则中间留下一个空的小正方形(阴影部分).设小长方形的长和宽分别为a和b(a>b).
(1)由图1,可知a,b满足的等量关系是 ;
(2)若图2中小正方形的边长为2,求小长方形的面积;
(3)用含b的代数式表示图2中小正方形的面积.
24.(本题14分)如图,数轴上有三点A,B,C,表示的数分别是,,3,请回答:
(1)若使C,B两点的距离等于A,B两点的距离,即,则需将点C向左移动_______个单位长度;
(2)点P是数轴上的一个动点,其表示的数为x,则的最小值是_______;
(3)若有两只小青蛙M,N,它们在数轴上的点表示的数分别为m,n,满足且的值最小,求两只小青蛙M,N之间的距离;
(4)点P,Q,R同时分别从A,B,C出发,点P以每秒5个单位长度向数轴正方向运动,点Q以每秒4个单位长度向数轴正方向运动,点R以每秒2个单位长度向数轴负方向运动,当时,求点R对应的数.
参考答案
1.A
2.D
3.D
4.B
5.B
6.B
7.C
8.C
9.D
10.B
12.-1
13.
14.
15.解:(1)将“”看作整体:,
由①得, ③
将③代入②得 ,即, ④
将④代入③,化简得,即,
将代入④得,
所以原方程组的解为 .
(2)
由①得, ③
将③代入②,整理得,解得,
将代入③得,
所以原方程组的解为.
16.解:∵(m﹣2)xn﹣1+2y|m﹣1|=m是关于x、y的二元一次方程,
∴n﹣1=1,|m﹣1|=1,
解得:n=2,m=0或2,
若m=2,方程为2y=2,不合题意,舍去,
则m=0,n=2.
17.解:解方程组得:,
代入中得:,
解得:.
18.解:设甲服装的成本是x元,乙服装的成本是y元,
根据题意可得:,
解得:.
答:甲服装的进价是300元,乙服装的进价是200元.
19.解:令x=0,得(0+1)3=d,得d=1,
令x=1,得(1+1)3=a+b+c+d,
∴a+b+c+d=8.
∴a+b+c=8-1=7.
20.解:由题意可得:
解得:.
答:A、B的值分别为,.
21.解:
(1)把A与B代入5A-2B得:
5A-2B
,
当且,5A-2B是常数,
∴,;
(2)关于的方程,
整理得:,
∴,
解方程,得,
根据题意得:,
解得:.
22.解:(1)由题可知:;
(2)由图2可知,,与(1)中联立方程组:
,
解得:,
所以小长方形的面积为60;
(3)设小正方形的边长为x,
由图2可知:,
则:,
∵
∴,代入,
得:,
所以小正方形的面积为:.
24.解:(1)∵A,B,C,表示的数分别是,,3,
∴,,
∵,
移动后点C表示的数为0或-4,
则需将点C向左移动3或7个单位长度;
故答案为:3或7;
(2)由数轴可知,点P在A, C,之间时, 的最小,
;
故答案为:7;
(3)由数轴可知,时,或,
∵的值最小,
∴点N与点B重合,;
两只小青蛙M,N之间的距离为3或6;
(4)设运动时间为t秒,点P,Q,R表示的数分别为:,,;
,,
∵
∴,
当时,,解得,;此时点R对应的数为;
当时,,解得,;此时点R对应的数为;
当时,,解得,;此时点R对应的数为.
一、单选题(共40分)
1.(本题4分)下列方程中,①;②;③;④,是二元一次方程的有( )
A.1个 B.2个 C.3个 D.4个
2.(本题4分)如果方程与下面方程中的一个组成的方程组的解为,这个方程可以是( )
A. B. C. D.
3.(本题4分)利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式放置,再交换两木块的位置,按图②所示的方式放置.测量的数据如图,则桌子的高度等于( )
A.70cm B.75cm C.80cm D.85cm
4.(本题4分)我国古代数学著作《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五,屈绳量之不足一尺,问木长几何?”大致意思是:“用一根绳子去量一根木条,绳子剩余4.5尺,将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”设绳子长为x尺,木条长为y尺,则根据题意所列方程组正确的是( )
A.B. C. D.
5.(本题4分)已知,则( )
A. B. C. D.
6.(本题4分)早餐店里,小明妈妈买了5个馒头,3个包子,老板少要1元,只要10元;小红爸爸买了8个馒头,6个包子,老板九折优惠,只要18元.若馒头每个x元,包子每个y元,则所列二元一次方程组正确的是( )
A. B. C. D.
7.(本题4分)已知关于,的方程组给出下列结论:
①当时,方程组的解也是的解;
②无论取何值,,的值不可能是互为相反数;
③,都为自然数的解有对.
正确的有几个( )
A. B. C. D.
8.(本题4分)如图1是2021年3月份的月历,小军同学用“”字形框在月历上框出四个数字,将该“”字形框上下左右移动,且一定要框住月历中的四个日期,若四个日期如图2所示,则下列关于,的关系正确的是( )
A. B. C. D.
9.(本题4分)若关于,的二元一次方程组的解也是二元一次方程的解,则的值为( ).
A. B. C. D.
10.(本题4分)甲、乙两人同求方程ax-by=7的整数解,甲正确地求出一个解为,乙把ax-by=7看成ax-by=1,求得一个解为,则a,b的值分别为( )
A. B. C. D.
二、填空题(共20分)
11.(本题5分)二元一次方程的正整数解为________.
12.(本题5分)已知是关于的二元一次方程的一个解,则的值为____.
13.(本题5分)如左下图是一个三阶幻方,图中每行、每列、每条对角线上的数字之和相等,则的值为_______.
14.(本题5分)在矩形ABCD中放入6个大小相同的长方形,尺寸如右上图所示。阴影部分的面积是
三、解答题(共90分)
15.(本题6分)解下列方程组:
(1) (2)
16.(本题6分)已知方程(m﹣2)xn﹣1+2y|m﹣1|=m是关于x、y的二元一次方程,求m、n的值.
17.(本题6分)若关于、的二元一次方程组与方程组有相同的解.求、的值.
18.(本题8分)甲、乙两件服装的进价共500元,商店老板将甲种服装按的利润定价,乙种服装按的利润定价,在实际出售时,应顾客要求,两件服装均按九折出售,这样商店老板共获利157元.求甲、乙两件服装的进价各是多少元?
19.(本题8分)已知(x+1)3=ax3+bx2+cx+d,求a+b+c的值.
20.(本题10分)已知等式对于一切有理数都成立,求A,B的值.
21.(本题10分)已知,且5A-2B的值是一个常数.
(1)求的值.
(2)关于x的方程的解与方程3m-2x=1-x的解互为相反数,求m的值.
22.(本题10分)已知,x无论取什么值,式子必为同一定值,求的值.
23.(本题12分)用8个形状和大小都相同的小长方形,恰好可以拼成如图1所示的大长方形;若用这8个小长方形拼成如图2所示的正方形,则中间留下一个空的小正方形(阴影部分).设小长方形的长和宽分别为a和b(a>b).
(1)由图1,可知a,b满足的等量关系是 ;
(2)若图2中小正方形的边长为2,求小长方形的面积;
(3)用含b的代数式表示图2中小正方形的面积.
24.(本题14分)如图,数轴上有三点A,B,C,表示的数分别是,,3,请回答:
(1)若使C,B两点的距离等于A,B两点的距离,即,则需将点C向左移动_______个单位长度;
(2)点P是数轴上的一个动点,其表示的数为x,则的最小值是_______;
(3)若有两只小青蛙M,N,它们在数轴上的点表示的数分别为m,n,满足且的值最小,求两只小青蛙M,N之间的距离;
(4)点P,Q,R同时分别从A,B,C出发,点P以每秒5个单位长度向数轴正方向运动,点Q以每秒4个单位长度向数轴正方向运动,点R以每秒2个单位长度向数轴负方向运动,当时,求点R对应的数.
参考答案
1.A
2.D
3.D
4.B
5.B
6.B
7.C
8.C
9.D
10.B
12.-1
13.
14.
15.解:(1)将“”看作整体:,
由①得, ③
将③代入②得 ,即, ④
将④代入③,化简得,即,
将代入④得,
所以原方程组的解为 .
(2)
由①得, ③
将③代入②,整理得,解得,
将代入③得,
所以原方程组的解为.
16.解:∵(m﹣2)xn﹣1+2y|m﹣1|=m是关于x、y的二元一次方程,
∴n﹣1=1,|m﹣1|=1,
解得:n=2,m=0或2,
若m=2,方程为2y=2,不合题意,舍去,
则m=0,n=2.
17.解:解方程组得:,
代入中得:,
解得:.
18.解:设甲服装的成本是x元,乙服装的成本是y元,
根据题意可得:,
解得:.
答:甲服装的进价是300元,乙服装的进价是200元.
19.解:令x=0,得(0+1)3=d,得d=1,
令x=1,得(1+1)3=a+b+c+d,
∴a+b+c+d=8.
∴a+b+c=8-1=7.
20.解:由题意可得:
解得:.
答:A、B的值分别为,.
21.解:
(1)把A与B代入5A-2B得:
5A-2B
,
当且,5A-2B是常数,
∴,;
(2)关于的方程,
整理得:,
∴,
解方程,得,
根据题意得:,
解得:.
22.解:(1)由题可知:;
(2)由图2可知,,与(1)中联立方程组:
,
解得:,
所以小长方形的面积为60;
(3)设小正方形的边长为x,
由图2可知:,
则:,
∵
∴,代入,
得:,
所以小正方形的面积为:.
24.解:(1)∵A,B,C,表示的数分别是,,3,
∴,,
∵,
移动后点C表示的数为0或-4,
则需将点C向左移动3或7个单位长度;
故答案为:3或7;
(2)由数轴可知,点P在A, C,之间时, 的最小,
;
故答案为:7;
(3)由数轴可知,时,或,
∵的值最小,
∴点N与点B重合,;
两只小青蛙M,N之间的距离为3或6;
(4)设运动时间为t秒,点P,Q,R表示的数分别为:,,;
,,
∵
∴,
当时,,解得,;此时点R对应的数为;
当时,,解得,;此时点R对应的数为;
当时,,解得,;此时点R对应的数为.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
