九年级数学下册人教版 26.2实际问题与反比例函数 练习题(Word版含答案)
文档属性
| 名称 | 九年级数学下册人教版 26.2实际问题与反比例函数 练习题(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 20.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 20:24:48 | ||
图片预览



文档简介
实际问题与反比例函数练习题
知识点1:反比例函数在实际问题中的应用
1.近视眼镜的度数y(度)与镜片焦距x(米)成反比例,其函数关系式为y=.如果近视眼镜镜片的焦距x=0.3米,那么近视眼镜的度数y为 .
2.某粮库需要把晾晒场上的1 200t玉米入库封存.
(1)入库所需要的时间d(单位:天)与入库平均速度v(单位:t/天)的函数解析式为 ;
(2)已知粮库有职工60名,每天最多可入库300t玉米,预计玉米入库最快可在 天内完成;
(3)粮库职工连续工作两天后,天气预报说未来几天会下雨,粮库决定次日把剩下的玉米全部入库,至少需要增加 名职工.
3.你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)x(mm2)的反比例函数,其图象如图所示.
(1)写出y与x的函数关系式;
(2)求当面条粗细为2 mm2时,面条的总长度是多少米?
(3)如果要求面条的粗细不得超过1.6 mm2,那么面条的总长度至少是多少米?
知识点2:反比例函数在物理学科中的应用
4.某密闭容器内装有一定质量的某种气体,当改变容积V时,气体的密度ρ是容积V的反比例函数,当容积为5 m3时,密度是1.4 kg/m3,则ρ与V之间的函数关系式为( ) ( )
A.ρ= B.ρ=7V C.ρ= D.ρ=
5.某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气球体积V的反比例函数,其图象如图所示,当气球内的气压大于160 kPa时,气球将爆炸,为了安全,气球的体积应该 ( )
A.不小于 m3 B.小于 m3 C.不大于 m3 D.小于 m3
6.实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例.一条长为100 cm的导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示,那么其函数关系式为 ,当S=2 cm2时,R= Ω.
易错点:忽略实际问题中自变量的取值范围
7.A,B两城间的距离为15千米,一人路行的平均速度每小时不少于3千米,也不多于5千米,则表示此人由A到B的路行速度x(千米/小时)与所用时间y(小时)的关系式y=的函数图象是( )
8.如图所示,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( )
9.如图,一块长方体大理石板的A,B,C三个面上的边长如图所示,如果大理石板的A面向下放在地上时地面所受压强为m帕,那么把大理石板B面向下放在地上时,地面所受压强是 ( )帕.
10.方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480千米,设小汽车的行驶时间为t(单位:小时),行驶速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.
(1)求v关于t的函数解析式;
(2)方方上午8点驾驶小汽车从A地出发.
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的取值范围;
②方方能否在当天11点30分前到达B地?说明理由.
11.教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10 ℃,加热到100 ℃停止加热,水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系,直至水温降至30 ℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30 ℃时接通电源,水温y(℃)与时间x(min)的关系如图所示.
(1)分别写出水温上升和下降阶段y与x之间的函数关系式;
(2)怡萱同学想喝高于50 ℃的水,请问她最多需要等待多长时间?
类型:反比例函数与一次函数的综合
12.已知点A是直线y=2x与双曲线y=(m为常数)一支的交点,过点A作x轴的垂线,垂足为B,且OB=2,则m的值为( )
A.-7 B.-8 C.8 D.7
13.函数y=-ax+a与y=(a≠0)在同一坐标系中的图象可能是 ( )
14.如图,直线y=kx-3(k≠0)与坐标轴分别交于点C,B,与双曲线y=-(x<0)交于点A(m,1),则AB的长是( )
A.2 B. C.2 D.
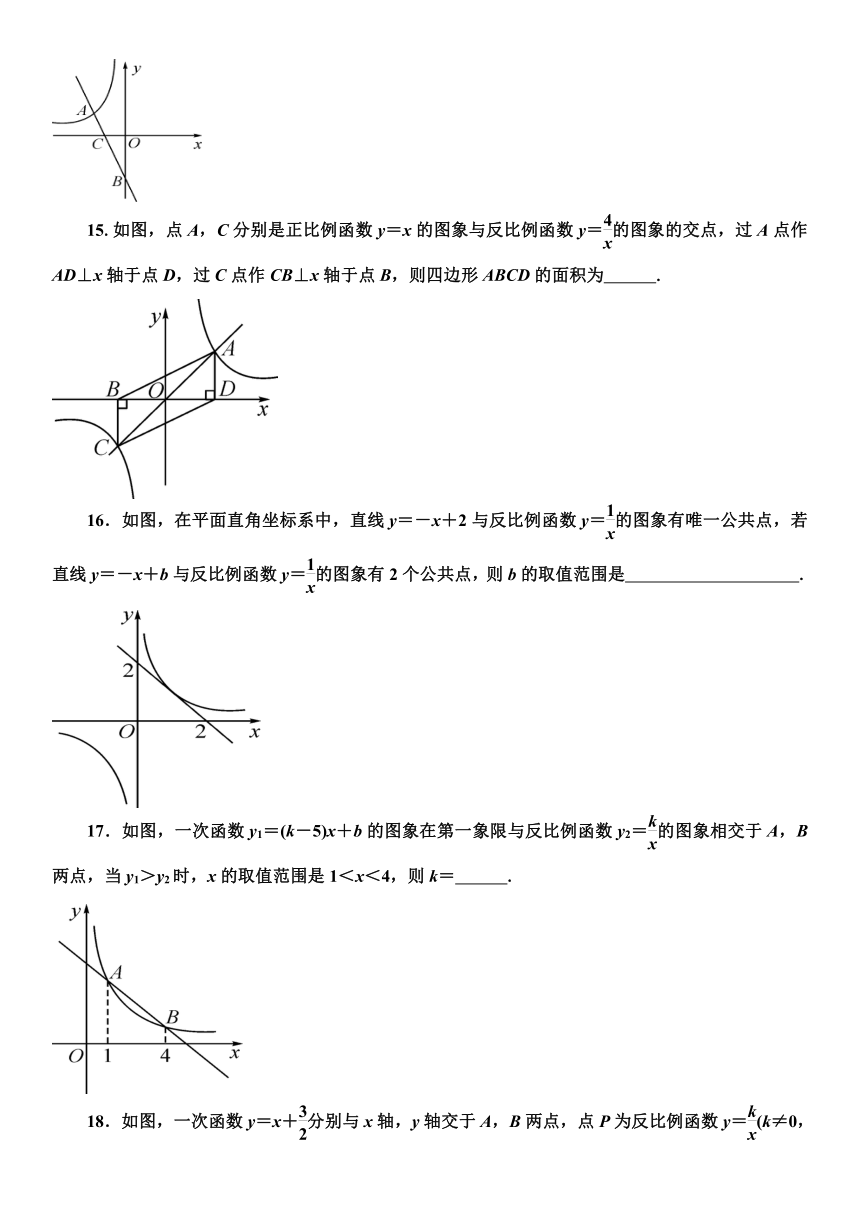
15.如图,点A,C分别是正比例函数y=x的图象与反比例函数y=的图象的交点,过A点作AD⊥x轴于点D,过C点作CB⊥x轴于点B,则四边形ABCD的面积为 .
16.如图,在平面直角坐标系中,直线y=-x+2与反比例函数y=的图象有唯一公共点,若直线y=-x+b与反比例函数y=的图象有2个公共点,则b的取值范围是 .
17.如图,一次函数y1=(k-5)x+b的图象在第一象限与反比例函数y2=的图象相交于A,B两点,当y1>y2时,x的取值范围是1<x<4,则k= .
18.如图,一次函数y=x+分别与x轴,y轴交于A,B两点,点P为反比例函数y=(k≠0,x<0)图象上一点,过点P作y轴的垂线交直线AB于点C,作PD⊥PC交直线AB于点D,若AC·BD=7,则k的值为 .
19.如图,已知反比例函数y=(k>0)的图象和一次函数y=-x+b的图象都过点P(1,m),过点P作y轴的垂线,垂足为A,O为坐标原点,△OAP的面积为1.
(1)求反比例函数和一次函数的解析式;
(2)设反比例函数图象与一次函数图象的另一交点为M,过M作x轴的垂线,垂足为B,求五边形OAPMB的面积.
20.在同一平面直角坐标系中,反比例函数y=(b≠0)与二次函数y=ax2+bx(a≠0)的图象大致是( ) ( )
21.★一次函数y=ax+b(a>0),二次函数y=ax2+bx和反比例函数y=(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( ) ( )
A.a>b>0 B.a>k>0 C.k>b>0 D.b=a+k
22.已知二次函数y=x2+2x+2与反比例函数y=(k≠0)的图象都经过点A(1,m).
(1)求反比例函数的解析式;
(2)当二次函数与反比例函数的值都随x的增大而减小时,求x的取值范围.
23.如图,已知正方形OABC的顶点A,C分别在x轴,y轴的正半轴上,且面积为16,点H是正方形OABC的中心,反比例函数y=经过点H,与AB,BC分别交于点E,F,过点H作HD⊥OA于点D,以DH为对称轴,且经过点E的抛物线L与反比例函数的图象交于点P.
(1)求k的值;
(2)若抛物线经过点F,求此时抛物线L的函数解析式;
(3)设抛物线L的顶点的纵坐标为m,点P的坐标为(x0,y0),当≤x0≤8,求m的取值范围.
答案:1、400 2、(1)d= (2)4(3)60
3、(1)解:由图象得,反比例函数图象经过点(4,32),设y与x的函数关系式是y=,则=32,解得k=128,
故y与x的函数关系式是y=.
(2)解:当x=2时,y==64,故当面条粗细为2 mm2时,面条的总长度是64米.
(3)解:当x=1.6时,y==80.
∴面条总长至少为80米.
4、C 5、A 6、(1)R=(2)14.5 7、D 8、A 9、3m
10、(1)解:v关于t的函数解析式为v=(t≥4).
(2)解:①将t=6代入v=,得v=80.
将t=代入v=,得v=100.
答:小汽车行驶速度v的取值范围为80≤v≤100.
②不能.理由:将t=代入v=,得v=>120.
答:方方不能在当天11点30分前到达B地.
11、(1)解:当0≤x≤7时,设y关于x的函数关系式为y=kx+b.
把(7,100),(0,30)代入,得解得
所以y=10x+30.当x>7时,设y=,
把(7,100)代入,得100=,得a=700,
所以y=.
当y=30时,x=,
∴y与x的函数关系式为y=
y与x的函数关系式每 min重复出现一次.
(2)解:将y=50代入y=10x+30,得x=2.
将y=50代入y=,得x=14.
14-2=12,-12=.
答:怡萱同学想喝高于50 ℃的水,她最多需要等待 min.
12、D 13、D 14、A 15、8 16、b>2或b<-2 17、4 18、- 19、(1)解:反比例函数的解析式为y=.
一次函数的解析式为y=-x+3.
(2)、解:设直线y=-x+3交x轴,y轴交于C,D两点,∴C(3,0),D(0,3).
联立两函数解析式,得
解得或∴P(1,2),M(2,1),
∴PA=1,AD=3-2=1,BM=1,BC=3-2=1,
∴五边形OAPMB的面积为S△COD-S△BCM-S△ADP=×3×3-×1×1-×1×1=.
20、D 21、B 22、(1)解:将A(1,m)代入y=x2+2x+2 得m=5,
将A(1,5)代入y=得k=5,
∴反比例函数的解析式y=.
(2)解:∵y=x2+2x+2=(x+1)2+1,∴抛物线的对称轴为直线x=-1,且开口向上,∴当x≤-1时,二次函数的值随x的增大而减小,
又∵当x<0时,y=函数值随x的增大而减小,∴当x≤-1时,二次函数与反比例函数的值都随x的增大而减小.
23、(1)解:∵正方形OABC面积为16,
∴A(4,0),B(4,4),C(0,4),H(2,2),
∵反比例函数y=经过点H,
∴k=4.
(2)解:由已知可知F(1,4),E(4,1),
∵DH为对称轴,设二次函数解析式为y=a(x-2)2+h,
∴∴
∴y=-x2+4x+1.
(3)解:由已知可知F(1,4),E(4,1),
∵DH为对称轴,设二次函数解析式为y=a(x-2)2+h,
∴∴
∴y=-x2+4x+1.
∵E(4,1)在函数y=a(x-2)2+m上,
∴a=,∴y=(x-2)2+m.
∴当P时,m=,
∴当P时,m=,
∴当≤x0≤8时,≤m≤.
知识点1:反比例函数在实际问题中的应用
1.近视眼镜的度数y(度)与镜片焦距x(米)成反比例,其函数关系式为y=.如果近视眼镜镜片的焦距x=0.3米,那么近视眼镜的度数y为 .
2.某粮库需要把晾晒场上的1 200t玉米入库封存.
(1)入库所需要的时间d(单位:天)与入库平均速度v(单位:t/天)的函数解析式为 ;
(2)已知粮库有职工60名,每天最多可入库300t玉米,预计玉米入库最快可在 天内完成;
(3)粮库职工连续工作两天后,天气预报说未来几天会下雨,粮库决定次日把剩下的玉米全部入库,至少需要增加 名职工.
3.你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)x(mm2)的反比例函数,其图象如图所示.
(1)写出y与x的函数关系式;
(2)求当面条粗细为2 mm2时,面条的总长度是多少米?
(3)如果要求面条的粗细不得超过1.6 mm2,那么面条的总长度至少是多少米?
知识点2:反比例函数在物理学科中的应用
4.某密闭容器内装有一定质量的某种气体,当改变容积V时,气体的密度ρ是容积V的反比例函数,当容积为5 m3时,密度是1.4 kg/m3,则ρ与V之间的函数关系式为( ) ( )
A.ρ= B.ρ=7V C.ρ= D.ρ=
5.某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气球体积V的反比例函数,其图象如图所示,当气球内的气压大于160 kPa时,气球将爆炸,为了安全,气球的体积应该 ( )
A.不小于 m3 B.小于 m3 C.不大于 m3 D.小于 m3
6.实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例.一条长为100 cm的导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示,那么其函数关系式为 ,当S=2 cm2时,R= Ω.
易错点:忽略实际问题中自变量的取值范围
7.A,B两城间的距离为15千米,一人路行的平均速度每小时不少于3千米,也不多于5千米,则表示此人由A到B的路行速度x(千米/小时)与所用时间y(小时)的关系式y=的函数图象是( )
8.如图所示,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( )
9.如图,一块长方体大理石板的A,B,C三个面上的边长如图所示,如果大理石板的A面向下放在地上时地面所受压强为m帕,那么把大理石板B面向下放在地上时,地面所受压强是 ( )帕.
10.方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480千米,设小汽车的行驶时间为t(单位:小时),行驶速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.
(1)求v关于t的函数解析式;
(2)方方上午8点驾驶小汽车从A地出发.
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的取值范围;
②方方能否在当天11点30分前到达B地?说明理由.
11.教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10 ℃,加热到100 ℃停止加热,水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系,直至水温降至30 ℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30 ℃时接通电源,水温y(℃)与时间x(min)的关系如图所示.
(1)分别写出水温上升和下降阶段y与x之间的函数关系式;
(2)怡萱同学想喝高于50 ℃的水,请问她最多需要等待多长时间?
类型:反比例函数与一次函数的综合
12.已知点A是直线y=2x与双曲线y=(m为常数)一支的交点,过点A作x轴的垂线,垂足为B,且OB=2,则m的值为( )
A.-7 B.-8 C.8 D.7
13.函数y=-ax+a与y=(a≠0)在同一坐标系中的图象可能是 ( )
14.如图,直线y=kx-3(k≠0)与坐标轴分别交于点C,B,与双曲线y=-(x<0)交于点A(m,1),则AB的长是( )
A.2 B. C.2 D.
15.如图,点A,C分别是正比例函数y=x的图象与反比例函数y=的图象的交点,过A点作AD⊥x轴于点D,过C点作CB⊥x轴于点B,则四边形ABCD的面积为 .
16.如图,在平面直角坐标系中,直线y=-x+2与反比例函数y=的图象有唯一公共点,若直线y=-x+b与反比例函数y=的图象有2个公共点,则b的取值范围是 .
17.如图,一次函数y1=(k-5)x+b的图象在第一象限与反比例函数y2=的图象相交于A,B两点,当y1>y2时,x的取值范围是1<x<4,则k= .
18.如图,一次函数y=x+分别与x轴,y轴交于A,B两点,点P为反比例函数y=(k≠0,x<0)图象上一点,过点P作y轴的垂线交直线AB于点C,作PD⊥PC交直线AB于点D,若AC·BD=7,则k的值为 .
19.如图,已知反比例函数y=(k>0)的图象和一次函数y=-x+b的图象都过点P(1,m),过点P作y轴的垂线,垂足为A,O为坐标原点,△OAP的面积为1.
(1)求反比例函数和一次函数的解析式;
(2)设反比例函数图象与一次函数图象的另一交点为M,过M作x轴的垂线,垂足为B,求五边形OAPMB的面积.
20.在同一平面直角坐标系中,反比例函数y=(b≠0)与二次函数y=ax2+bx(a≠0)的图象大致是( ) ( )
21.★一次函数y=ax+b(a>0),二次函数y=ax2+bx和反比例函数y=(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( ) ( )
A.a>b>0 B.a>k>0 C.k>b>0 D.b=a+k
22.已知二次函数y=x2+2x+2与反比例函数y=(k≠0)的图象都经过点A(1,m).
(1)求反比例函数的解析式;
(2)当二次函数与反比例函数的值都随x的增大而减小时,求x的取值范围.
23.如图,已知正方形OABC的顶点A,C分别在x轴,y轴的正半轴上,且面积为16,点H是正方形OABC的中心,反比例函数y=经过点H,与AB,BC分别交于点E,F,过点H作HD⊥OA于点D,以DH为对称轴,且经过点E的抛物线L与反比例函数的图象交于点P.
(1)求k的值;
(2)若抛物线经过点F,求此时抛物线L的函数解析式;
(3)设抛物线L的顶点的纵坐标为m,点P的坐标为(x0,y0),当≤x0≤8,求m的取值范围.
答案:1、400 2、(1)d= (2)4(3)60
3、(1)解:由图象得,反比例函数图象经过点(4,32),设y与x的函数关系式是y=,则=32,解得k=128,
故y与x的函数关系式是y=.
(2)解:当x=2时,y==64,故当面条粗细为2 mm2时,面条的总长度是64米.
(3)解:当x=1.6时,y==80.
∴面条总长至少为80米.
4、C 5、A 6、(1)R=(2)14.5 7、D 8、A 9、3m
10、(1)解:v关于t的函数解析式为v=(t≥4).
(2)解:①将t=6代入v=,得v=80.
将t=代入v=,得v=100.
答:小汽车行驶速度v的取值范围为80≤v≤100.
②不能.理由:将t=代入v=,得v=>120.
答:方方不能在当天11点30分前到达B地.
11、(1)解:当0≤x≤7时,设y关于x的函数关系式为y=kx+b.
把(7,100),(0,30)代入,得解得
所以y=10x+30.当x>7时,设y=,
把(7,100)代入,得100=,得a=700,
所以y=.
当y=30时,x=,
∴y与x的函数关系式为y=
y与x的函数关系式每 min重复出现一次.
(2)解:将y=50代入y=10x+30,得x=2.
将y=50代入y=,得x=14.
14-2=12,-12=.
答:怡萱同学想喝高于50 ℃的水,她最多需要等待 min.
12、D 13、D 14、A 15、8 16、b>2或b<-2 17、4 18、- 19、(1)解:反比例函数的解析式为y=.
一次函数的解析式为y=-x+3.
(2)、解:设直线y=-x+3交x轴,y轴交于C,D两点,∴C(3,0),D(0,3).
联立两函数解析式,得
解得或∴P(1,2),M(2,1),
∴PA=1,AD=3-2=1,BM=1,BC=3-2=1,
∴五边形OAPMB的面积为S△COD-S△BCM-S△ADP=×3×3-×1×1-×1×1=.
20、D 21、B 22、(1)解:将A(1,m)代入y=x2+2x+2 得m=5,
将A(1,5)代入y=得k=5,
∴反比例函数的解析式y=.
(2)解:∵y=x2+2x+2=(x+1)2+1,∴抛物线的对称轴为直线x=-1,且开口向上,∴当x≤-1时,二次函数的值随x的增大而减小,
又∵当x<0时,y=函数值随x的增大而减小,∴当x≤-1时,二次函数与反比例函数的值都随x的增大而减小.
23、(1)解:∵正方形OABC面积为16,
∴A(4,0),B(4,4),C(0,4),H(2,2),
∵反比例函数y=经过点H,
∴k=4.
(2)解:由已知可知F(1,4),E(4,1),
∵DH为对称轴,设二次函数解析式为y=a(x-2)2+h,
∴∴
∴y=-x2+4x+1.
(3)解:由已知可知F(1,4),E(4,1),
∵DH为对称轴,设二次函数解析式为y=a(x-2)2+h,
∴∴
∴y=-x2+4x+1.
∵E(4,1)在函数y=a(x-2)2+m上,
∴a=,∴y=(x-2)2+m.
∴当P时,m=,
∴当P时,m=,
∴当≤x0≤8时,≤m≤.
