2021-2022学年沪科版七年级数学上册2.2.4 整式的加减 同步测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版七年级数学上册2.2.4 整式的加减 同步测试卷(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 82.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 00:00:00 | ||
图片预览


文档简介
2.2.4 整式的加减同步测试卷 2021-2022学年沪科版七年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共7小题,共35分)
多项式--1与-2a+1的和为( )
A. B. C. D.
减去-2x等于-+2x+1的多项式是( )
A. B. C. D.
已知a-2b=3,则3(a-b)-(a+b)的值为( )
A. B. C. D.
一个多项式与-2x+1的和是3x-2,则这个多项式为( )
A. B. C. D.
若A=-4a+3,B=-4a+2,则A与B的大小关系是( )
A. B. C. D. 不能确定
某校组织若干师生到活动基地进行社会实践活动.若学校租用45座的客车x辆,则余下20人无座位;若租用60座的客车则可少租用2辆,且最后一辆还没坐满,则乘坐最后一辆60座客车的人数是( )
A. B. C. D.
如果多项式A与多项式B的和是3x+,多项式B与多项式C的和是-x+,那么多项式A减去多项式C的差是( )
A. B. C. D.
二、填空题(本大题共6小题,共30分)
若2x+3y=5,则6x-4y-2(x-5y)= .
已知m是系数,关于x,y的两个多项式-2x+y与-+2x+3y的差中不含二次项,则整式+3m-1的值为 .
已知一个两位数M的个位上的数字是a,十位上的数字是b,交换这个两位数的个位与十位上的数字的位置,所得的新数记为N,则2M-N= .(用含a和b的式子表示)
下列数阵用1~2016中的整数按连续排列的方式组成“自然数阵”,现用“X”型框任意框出5个数.
如果用表示类似“X”形框中的5个数,请用含m的代数式表示a+b+c+d= .
若+mn=-7,-5mn=-17,则+6mn-= .
用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=.
例如:(-3)☆2==2.
从-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,8中任选两个有理数作a,b(ab)的值,并计算a☆b,那么所有运算结果中的最大值是 .
三、解答题(本大题共7小题,共55分)
先化简,再求值:
(1)-[+2(1-)+],其中x=4,y=-;
(2)已知|a-1|+=0,求-a-2-的值.
已知某三角形的一条边长为m+n,另一条边长比这条边长大m-3,第三条边长等于2n-m,求这个三角形的周长.
已知小明的年龄是m岁,小红的年龄比小明的年龄的2倍少4岁,小华的年龄比小红年龄的还多1岁,这三名同学的年龄之和是多少
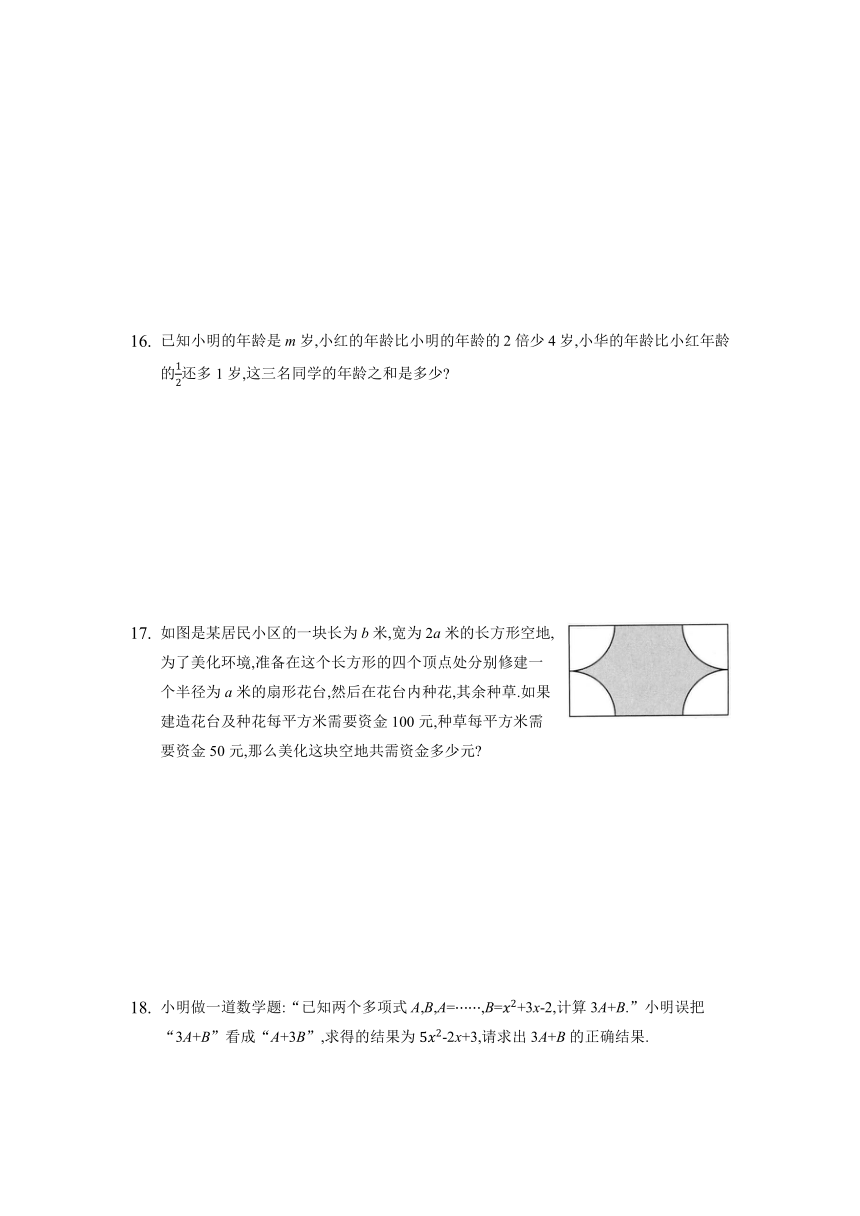
如图是某居民小区的一块长为b米,宽为2a米的长方形空地,为了美化环境,准备在这个长方形的四个顶点处分别修建一个半径为a米的扇形花台,然后在花台内种花,其余种草.如果建造花台及种花每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元
小明做一道数学题:“已知两个多项式A,B,A=,B=+3x-2,计算3A+B.”小明误把“3A+B”看成“A+3B”,求得的结果为-2x+3,请求出3A+B的正确结果.
(1)当x=1时,多项式+qx+1的值为2023,求当x=-1时,多项式+qx+1的值;
(2)求当式子+5取最小值时,式子5x-[--(-5x+2)]的值.
如图是某月的月历.
(1)带阴影的十字框中的5个数之和与十字框中心的数有什么关系
(2)不改变十字框的大小,如果将带阴影的十字框移至其他几个位置试一试,你能得出什么结论 你知道为什么吗
(3)这个结论对于任何一个月的月历都成立吗
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】C
5.【答案】B
6.【答案】C
7.【答案】A
8.【答案】10
9.【答案】-1
10.【答案】19b-8a
11.【答案】4m
12.【答案】10
13.【答案】8
14.【答案】(1)解:原式=--2+-=-2;
把x=4,y=-代人-2,
得原式=34-2=1.
(2)解:因为|a-1|+=0,
所以a-1=0,b+3=0.
解得a=1,b=-3.
原式=-a-2a+-a+=-4a+.
当a=1,b=-3时,
原式=-4+9=-4+12=8.
15.【答案】解:(m+n)+(m-3)+(m+n)+(2n-m)
=m+n+m-3+m+n+2n-m
=2m+4n-3.
答:这个三角形的周长为2m+4n-3.
16.【答案】解:m+(2m-4)+=m+2m-4+m-2+1=4m-5.
答:这三名同学的年龄之和是(4m-5)岁.
17.【答案】解:花台面积为平方米,草地面积为(2ab-)平方米.
美化这块空地共需资金100+50(2ab-)=(50+100ab)元.
18.【答案】解:A=-2x+3-3(+3x-2)
=-2x+3--9x+6
=-11x+9.
3A+B=3(-11x+9)++3x-2
=-33x+27++3x-2
=-30x+25.
19.【答案】解:(1)因为当x=1时,多项式+qx+1的值为2023,所以p+q1+1=2023,
则p+q=2022.
当x=-1时,+qx+1=p+q(-1)+1
=-p-q+1=-(p+q)+1=-2022+1=-2021.
(2)因为+5取得最小值时,=0,
所以2x+4=0,
解得x=-2.
原式=5x-(-+5x-2)=5x+-5x+2=+2.
当x=-2时,原式=2+2=10.
20.【答案】解:(1)带阴影的十字框中的5个数之和是十字框中心的数的5倍.
(2)带阴影的十字框中的5个数之和是十字框中心的数的5倍,
理由如下:设十字框中心的数为x,则其余4个数分别为x-7,x-1,x+1,x+7,带阴影的十字框中的5个数之和为(x-7)+(x-1)+x+(x+1)+(x+7)=5x,所以带阴影的十字框中的5个数之和是十字框中心的数的5倍.
(3)这个结论对于任何一个月的月历都成立.
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共7小题,共35分)
多项式--1与-2a+1的和为( )
A. B. C. D.
减去-2x等于-+2x+1的多项式是( )
A. B. C. D.
已知a-2b=3,则3(a-b)-(a+b)的值为( )
A. B. C. D.
一个多项式与-2x+1的和是3x-2,则这个多项式为( )
A. B. C. D.
若A=-4a+3,B=-4a+2,则A与B的大小关系是( )
A. B. C. D. 不能确定
某校组织若干师生到活动基地进行社会实践活动.若学校租用45座的客车x辆,则余下20人无座位;若租用60座的客车则可少租用2辆,且最后一辆还没坐满,则乘坐最后一辆60座客车的人数是( )
A. B. C. D.
如果多项式A与多项式B的和是3x+,多项式B与多项式C的和是-x+,那么多项式A减去多项式C的差是( )
A. B. C. D.
二、填空题(本大题共6小题,共30分)
若2x+3y=5,则6x-4y-2(x-5y)= .
已知m是系数,关于x,y的两个多项式-2x+y与-+2x+3y的差中不含二次项,则整式+3m-1的值为 .
已知一个两位数M的个位上的数字是a,十位上的数字是b,交换这个两位数的个位与十位上的数字的位置,所得的新数记为N,则2M-N= .(用含a和b的式子表示)
下列数阵用1~2016中的整数按连续排列的方式组成“自然数阵”,现用“X”型框任意框出5个数.
如果用表示类似“X”形框中的5个数,请用含m的代数式表示a+b+c+d= .
若+mn=-7,-5mn=-17,则+6mn-= .
用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=.
例如:(-3)☆2==2.
从-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,8中任选两个有理数作a,b(ab)的值,并计算a☆b,那么所有运算结果中的最大值是 .
三、解答题(本大题共7小题,共55分)
先化简,再求值:
(1)-[+2(1-)+],其中x=4,y=-;
(2)已知|a-1|+=0,求-a-2-的值.
已知某三角形的一条边长为m+n,另一条边长比这条边长大m-3,第三条边长等于2n-m,求这个三角形的周长.
已知小明的年龄是m岁,小红的年龄比小明的年龄的2倍少4岁,小华的年龄比小红年龄的还多1岁,这三名同学的年龄之和是多少
如图是某居民小区的一块长为b米,宽为2a米的长方形空地,为了美化环境,准备在这个长方形的四个顶点处分别修建一个半径为a米的扇形花台,然后在花台内种花,其余种草.如果建造花台及种花每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元
小明做一道数学题:“已知两个多项式A,B,A=,B=+3x-2,计算3A+B.”小明误把“3A+B”看成“A+3B”,求得的结果为-2x+3,请求出3A+B的正确结果.
(1)当x=1时,多项式+qx+1的值为2023,求当x=-1时,多项式+qx+1的值;
(2)求当式子+5取最小值时,式子5x-[--(-5x+2)]的值.
如图是某月的月历.
(1)带阴影的十字框中的5个数之和与十字框中心的数有什么关系
(2)不改变十字框的大小,如果将带阴影的十字框移至其他几个位置试一试,你能得出什么结论 你知道为什么吗
(3)这个结论对于任何一个月的月历都成立吗
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】C
5.【答案】B
6.【答案】C
7.【答案】A
8.【答案】10
9.【答案】-1
10.【答案】19b-8a
11.【答案】4m
12.【答案】10
13.【答案】8
14.【答案】(1)解:原式=--2+-=-2;
把x=4,y=-代人-2,
得原式=34-2=1.
(2)解:因为|a-1|+=0,
所以a-1=0,b+3=0.
解得a=1,b=-3.
原式=-a-2a+-a+=-4a+.
当a=1,b=-3时,
原式=-4+9=-4+12=8.
15.【答案】解:(m+n)+(m-3)+(m+n)+(2n-m)
=m+n+m-3+m+n+2n-m
=2m+4n-3.
答:这个三角形的周长为2m+4n-3.
16.【答案】解:m+(2m-4)+=m+2m-4+m-2+1=4m-5.
答:这三名同学的年龄之和是(4m-5)岁.
17.【答案】解:花台面积为平方米,草地面积为(2ab-)平方米.
美化这块空地共需资金100+50(2ab-)=(50+100ab)元.
18.【答案】解:A=-2x+3-3(+3x-2)
=-2x+3--9x+6
=-11x+9.
3A+B=3(-11x+9)++3x-2
=-33x+27++3x-2
=-30x+25.
19.【答案】解:(1)因为当x=1时,多项式+qx+1的值为2023,所以p+q1+1=2023,
则p+q=2022.
当x=-1时,+qx+1=p+q(-1)+1
=-p-q+1=-(p+q)+1=-2022+1=-2021.
(2)因为+5取得最小值时,=0,
所以2x+4=0,
解得x=-2.
原式=5x-(-+5x-2)=5x+-5x+2=+2.
当x=-2时,原式=2+2=10.
20.【答案】解:(1)带阴影的十字框中的5个数之和是十字框中心的数的5倍.
(2)带阴影的十字框中的5个数之和是十字框中心的数的5倍,
理由如下:设十字框中心的数为x,则其余4个数分别为x-7,x-1,x+1,x+7,带阴影的十字框中的5个数之和为(x-7)+(x-1)+x+(x+1)+(x+7)=5x,所以带阴影的十字框中的5个数之和是十字框中心的数的5倍.
(3)这个结论对于任何一个月的月历都成立.
第2页,共2页
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
