2021-2022学年沪科版七年级数学上册3.2 一元一次方程的应用 同步测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版七年级数学上册3.2 一元一次方程的应用 同步测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 119.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 15:36:17 | ||
图片预览




文档简介
3.2 一元一次方程的应用同步测试卷 2021-2022学年沪科版七年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共7小题,共21分)
某地修一条公路,若甲工程队单独承包要80天完成,乙工程队单独承包要120天完成.现在由甲、乙工程队合作承包,完成任务需要( )
A. 天 B. 天 C. 天 D. 天
要挖一条水渠,共有72人参加挖土和运土,已知3人挖出的土1人恰好能全部运走,怎样调动人员才能使挖出的土能及时运走 解决此问题,可设派x人挖土,其他的人运土,可列方程( )
A. B. C. D.
从甲地到乙地,公共汽车原需行驶7h,开通高速公路后,车速平均每时增加了20km,只需5h即可到达,则甲、乙两地的路程是( )
A. B. C. D.
某中学的学生军训,沿着与笔直的铁路并列的公路匀速前进,每小时走4500米,一列火车以每小时120千米的速度迎面开来,测得火车与队首学生相遇,到车尾与队末学生相遇共经过60秒,如果队伍长500米, 那么火车长( )
A. 米 B. 米 C. 米 D. 米
甲班有54人,乙班有48人,要使甲班人数是乙班的2倍,设从乙班调往甲班人数x,可列方程( )
A. B.
C. D.
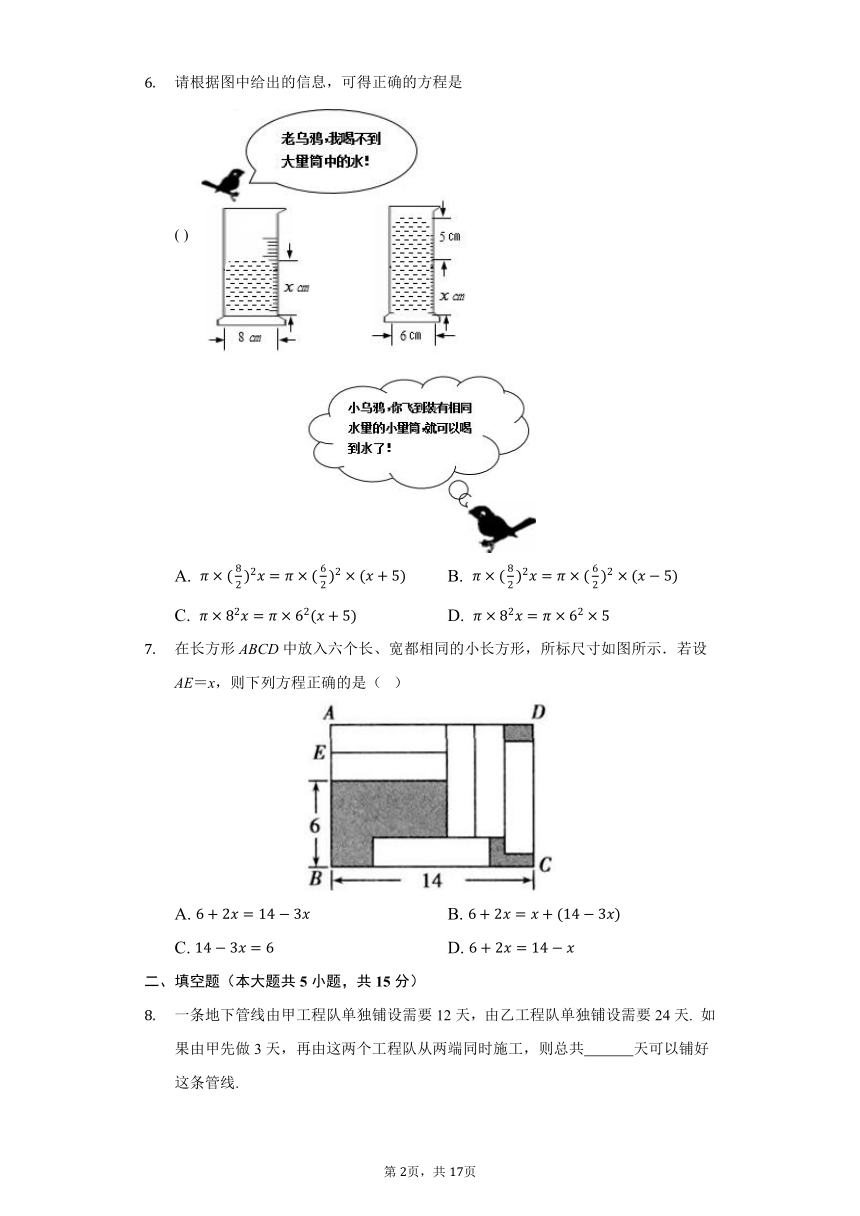
请根据图中给出的信息,可得正确的方程是( )
A. B.
C. D.
在长方形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示.若设AE=x,则下列方程正确的是( )
A. B.
C. D.
二、填空题(本大题共5小题,共15分)
一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天. 如果由甲先做3天,再由这两个工程队从两端同时施工,则总共 天可以铺好这条管线.
明代大数学家程大位著的《算法统宗》一书中,记载了这样一道数学题:“八万三千短竹竿,将来要把笔头安,管三套五为期定,问郡多少能完成.”用现代的话说就是:有83000根短竹,每根短竹可制成毛笔的笔管3个或笔套5个,怎样安排制作笔管或笔套的短竹的数量,使制成的笔管与笔套正好配套 设用于制作笔管的短竹数为x根,则可列方程为 .
已知A、B两地相距1000米,甲、乙两人分别从A、B两地同时出发,沿着同一条直线公路相向而行.若甲以7米/秒的速度骑自行车前进,乙以3米/秒的速度步行,则经过 秒两人相距100米.
一列火车长240米,速度为60千米/时,一辆越野车的速度为80千米/时,当火车前进时,越野车与火车同时同向而行,由火车尾追至火车头需要__________秒.(越野车车身长不计)
某校准备组织七年级学生观看电影《我和我的祖国》,由各班班长负责买票,一班班长问售票员买团体票是否可以优惠.售票员说:“50人以上的团体票有两个优惠方案可选择,方案一:全体人员可打8折;方案二:若打9折,有6人可以免票.”
一班班长思考了一会儿,说:“我们班无论选择哪种方案要付的钱是一样的.”则一班有 人.
三、解答题(本大题共20小题,共84分)
整理一批数据,由一人做需80h完成,现在计划先由一些人做2h,再增加5人做8h,可以完成这项工作的,问怎样安排参与整理数据的具体人数?
某报社需要在40 min内将一篇紧急宣传文稿输入电脑.已知独立完成此项任务,小王需要50 min,小李需要30 min.小王独自输入了30 min后,因为急于完成任务,请求小李帮助他(求助时间忽略不计),他们能在要求的时间内完成任务吗 请说明理由.
为实施乡村振兴战略,解决某山区老百姓出行难的问题,当地政府决定修建一条高速公路.其中一段长为146 m的山体隧道贯穿工程由甲、乙两个工程队负责施工.甲工程队独立工作2天后,乙工程队加入,两工程队又联合工作了1天,这3天共掘进26 m.已知甲工程队每天比乙工程队多掘进2 m,按此速度完成这项隧道贯穿工程,甲、乙两个工程队还需联合工作多少天
在某城市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天,乙队单独完成这项工程需要90天.
(1)若由甲队先做20天,剩下的工程由甲、乙两队合作完成.甲、乙两队合作多少天
(2)甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱 还是由甲、乙两队全程合作完成该工程省钱
有一个加工茶杯的车间,一个工人每小时平均可以加工杯身12个或加工杯盖15个,车间共有90人.安排加工杯身的人数为多少时,才能使生产的杯身和杯盖正好配套
解法一:设安排加工杯身的工人为x人,则加工杯盖的工人为 人, 每小时加工杯身 个,杯盖 个,则可列方程为 .解得x= .
解法二:设共加工杯身x个(或共加工杯盖x个),则加工杯身的工人为 人,加工杯盖的工人为 人,则可列方程为 .解得x= .故加工杯身的工人为 人.
红光服装厂要生产某种型号学生服一批,已知每3米长的布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,计划用600米长的这种布料生产学生服,应分别用多少布料生产上衣和裤子,才能使上衣和裤子恰好配套?共能生产多少套?
甲、乙两地相距200 km,快车速度为120 km/h,慢车速度为80 km/h,慢车从甲地出发,快车从乙地出发,
(1)如果两车同时出发,相向而行,出发后几时两车相遇?相遇时离甲地多远?
(2)如果两车同时出发,同向(从乙开始向甲方向)而行,出发后几时两车相遇?
一轮船往返于甲、乙两码头之间,顺水航行需要3 h,逆水航行比顺水航行多用30 min,若轮船在静水中的速度为26 km/h,求水流的速度.
A,B两地间的路程为360千米,甲车从A地出发开往B地,每小时行驶72千米.甲车出发25分钟后,乙车从B地出发开往A地,每小时行驶48千米.
(1)几小时后两车相遇?
(2)两车相遇后,各自仍按原速度和原方向继续行驶.那么相遇以后两车相距100千米时,甲车从出发共行驶了多少小时?
李先生从家到公司去上班要先经过一段平路再过一段下坡路。他走平路每分钟走m,下坡路每分钟走m,上坡路每分钟走m,从家到公司需要分钟,从公司到家里需要 分钟,求李先生家离公司多远。
某中学学生步行到郊外旅行,七年级(1)班学生组成前队,步行速度为4千米/小时,七(2)班的学生组成后队,速度为6千米/小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米/小时.
(1)后队追上前队需要多长时间?
(2)后队追上前队的时间内,联络员走的路程是多少?
(3)七年级(1)班出发多少小时后两队相距2千米?
甲、乙两厂共同加工一批产品.甲厂有91名工人,乙厂有49名工人,为了赶制这批产品又调来了100名工人,要使甲厂的人数比乙厂人数的3倍少12人,应往甲、乙两厂各调多少名工人
某中学组织七年级学生去春游,原计划租用45座客车若干辆,但会有15人没有座位;如果租用同样数量的60座客车,则会多出一辆,且其余客车恰好坐满.已知45座客车日租金为每辆220元,60座客车日租金为每辆300元.问:
(1)七年级学生有多少人 按原计划需要租用45座客车多少辆
(2)要使每位学生都有座位,怎样租车更合算
一个底面直径为16厘米的圆柱形木桶内装满水,水中淹没着一个底面直径为8厘米,高为15厘米的铁质小圆柱体.当铁质小圆柱体被取出后,木桶内的水面下降了多少?
某药业集团生产的某种药品包装盒的形状是长方体,且侧面展开图如图所示.如果长方体盒子的长比宽多4 cm,求这种药品包装盒的体积.
要利用墙和篱笆为一个长方形的养鸡场(长方形的一边利用墙,三边用篱笆),现有一段长14m的墙和一段长为35m的篱笆可以利用.小王打算使围成鸡场的长比宽多5m,小赵打算使围成鸡场的长比宽多2m,你认为谁的设计符合实际?按照他的设计,鸡场的面积是多少?
在一个底面直径为5cm,高为18cm的圆柱瓶内装满水,再将瓶内的水倒入一个底面直径为6cm,高为10cm的圆柱玻璃杯中,能否完全装下 若装不下,则瓶内水还剩多高 若不能装满,求杯内水面离杯口的距离.
李老师准备购买一套小户型商品房,他去售楼处了解情况得知,该户型商品房的单价是5000元/,如图所示(单位:m,卫生间的宽未定,设宽为x m),售楼处为李老师提供了以下两种优惠方案:
方案一:整套房的单价为5000元/,其中卫生间可免费赠送一半的面积;
方案二:整套房按原销售总金额的9.5折出售.
(1)用含x的式子表示该户型商品房的面积及按方案一、方案二购买一套该户型商品房的总金额;
(2)当x=2时,通过计算说明哪种方案较优惠,优惠多少元.
为庆祝商都正式营业,商都推出了两种购物方案.
方案一:非会员购物所有商品价格可获九五折优惠;
方案二:交纳300元会员费成为该商都会员,所有商品价格可获九折优惠.
(1)以x(元)表示商品价格,分别用含有x的式子表示两种购物方案中的支出金额;
(2)若某人计划在商都购买价格为5880元的电视机一台,请分析选择哪种方案较省钱;
(3)哪种情况下,两种方案的支出金额相同
32.在“十·一”黄金周期间,某超市推出如下购物优惠方案:(1)一次性购物在100元(不含100元)以内时,不享受优惠;(2)一次性购物在100元(含100元)以上,300元(不含300元)以内时,一律享受九折的优惠;(3)一次性购物在300元(含300元)以上时,一律享受八折的优惠.王茜在本超市两次购物分别付款80元、252元.如果王茜改成在本超市一次性购买与上两次完全相同的商品,则应付款多少元?
1.【答案】A
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】A
6.【答案】A
7.【答案】B
8.【答案】
9.【答案】3x=5(83000-x)
10.【答案】 90或110
11.【答案】 43.2
12.【答案】54
13.【答案】解:设先安排x人参与整理数据,由题意得:×2+×(x+5)×8=,
解得:x=2.
答:计划先由2人整理这组数据.
14.【答案】解:能.
理由:设小李加入后,x min完成任务,
根据题意,
得+=1,解得x=7.5,
则他们完成共用时37.5 min.
因为37.5<40,
所以他们能在要求的时间内完成任务.
15.【答案】解:设甲工程队每天掘进xm,则乙工程队每天掘进(x-2)m.
由题意得2x+(x+x-2)=26
解得x=7
则乙工程队每天掘进5m
(天)
故甲乙两个工程队还需联合工作10天
16.【答案】解:(1)设甲、乙两队合作t天,
由题意得
解得:t=24.
(2)设甲、乙合作完成需y天,则有
解得,y=36,
①甲单独完成需付工程款为60×3.5=210(万元).
②乙单独完成超过计划天数不符合题意.
③甲、乙合作完成需付工程款为36×(3.5+2)=198(万元).
答:在不超过计划天数的前提下,由甲、乙合作完成最省钱.
17.【答案】解:(90-x);12x;15(90-x);12x=15(90-x);50;
;;+=90;600;50.
18.【答案】解:设用x米布料生产上衣,根据题意得:
解得:x=360,
答:用360米布料生产上衣,240米布料生产裤子,才能使上衣和裤子恰好配套。
19.【答案】 解:(1)设出发后x小时两车相遇,
由题意得:120x+80x=200,
解得:x=1,80×1=80(千米),
答:两车同时出发,相向而行,出发后1小时两车相遇;相遇时离甲地80千米;
(2)设出发后y时两车相遇,
由题意得:120y=200+80y,
解得:y=5,
答:出发后5小时两车相遇.
20.【答案】解:设水流速度为x km/h,
则船在顺水中的速度为 km/h,船在逆水中的速度为 km/h,
由题意得,,
解得,
所以水流速度为2 km/h.
21.【答案】解:(1)=330÷120
=(小时),
答:小时后两车相遇.
(2)解:设甲车从出发共行驶了x小时.
根据题意,得25分钟=小时,
72x+48(x-)=360+100,
72x+48x-20=460,
120x=480,
x=4.
答:甲车从出发共行驶4小时.
22.【答案】解:设下坡路长为米,则,
∴。
下坡时间(分钟)
平路时间(分钟)
平路长度(米)
总路程=平路长度+下坡长度 (米)
∴李先生家离公司 米。
23.【答案】解:(1)设后队追上前队需要x小时,
根据题意得:(6-4)x=4×1
∴x=2
答:后队追上前队需要2小时,
(2)10×2=20千米
答:联络员走的路程是20千米,
(3)设七年级(1)班出发t 小时后,两队相距2千米,
当七年级(2)班没有出发时,t==,
当七年级(2)班出发,但没有追上七年级(1)班时,4t=6(t-1)+2
∴t=2,
当七年级(2)班追上七年级(1)班后,6(t-1)=4t+2
∴t=4,
答:七年级(1)班出发小时或2小时或4小时后,两队相距2千米.
24.【答案】解:设应往甲厂调x名工人,则往乙厂调(100-x)名工人,
依题意,得91+x=3(49+100-x)-12.
解这个方程,得x=86.
所以100-x=14.
故应往甲厂调86名工人,往乙厂调14名工人.
25.【答案】解:(1)设原计划租用45座客车x辆,根据题意得
60(x-1)=45x+15,
解得x=5,
七年级人数是455+15=240(人),
答:七年级有学生240人,原计划租用45座客车5辆;
(2)租45座客车:240÷45≈5.3(辆),
所以需租6辆,租金为220×6=1320(元),
租60座客车:240÷60=4(辆),
所以需租4辆,租金为300×4=1200(元),
租45座客车4辆,租金:220×4=880元,
租60座客车1辆,租金:300元,
880+300=1180<1200<1320,
答:租用4辆45座客车租1辆60座客车更合算.
26.【答案】解:设当小圆柱体取出后,木桶内水面降低xcm,根据题意可得:
π×42×15=π×82x,
解得:x=.
答:木桶内的水面下降了厘米.
27.【答案】解:这种药品包装盒的体积为.
28.【答案】解: 设宽为xm,根据小王的方案可列方程
2x+x+5=35,解得x=10
所以x+5=15>14,所以这个方案不符合实际.
根据小王的方案可列方程2x+x+2=35,
解得x=11所以x+2=13<14,
所以这个方案符合实际,其面积为11×13=143(m2).
答:小赵的方案符合实际,其面积为11×13=143(m2).
29.【答案】解:根据题意得
圆柱形瓶内的体积为=,
圆柱形玻璃杯的体积为=,
因为,
故不能装下.
将圆柱形玻璃杯的水装满后,圆柱形瓶内水
的体积还有:,
故瓶中还剩水的高度为:.
30.【答案】解:(1)该户型商品房的面积为47+3(8-4)+2(7-3)+(8-4-2)x=48+2x().
该户型商品房的卫生间面积为(8-4-2)x=2x().
按方案一购买一套该户型商品房的总金额为5000=240000+5000x(元);
按方案二购买一套该户型商品房的总金额为(48+2x)500095%=228000+9500x(元).
(2)当x=2时,方案一总金额为240000+5000x=250000(元);
方案二总金额为228000+9500x=247000(元).
方案二比方案一优惠250000-247000=3000(元).
所以方案二较优惠,优惠3000元.
31.【答案】解:(1)方案一:0.95x元,
方案二:(0.9x+300)元;
(2)当x=5880时,
方案一支出金额为0.955880=5586(元),
方案二支出金额为0.95880+300=5592(元).
因为5592元>5586元,
所以选择方案一较省钱;
(3)由题意,得0.95x=0.9x+300,解得x=6000.
答:当商品价格是6000元时,两种方案的支出金额相同.
32.【答案】解:设应付款x元.
(1)若第2次购物没有超过300元,根据题意,得
x÷ =80+252÷,
解得,x=288(元),
(2)若第2次购物超过300元,根据题意,得
x÷ =80+252÷,
解得,x=316元),
答:王茜改成在本超市一次性购买与上两次完全相同的商品,则应付款288元或316元.
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共7小题,共21分)
某地修一条公路,若甲工程队单独承包要80天完成,乙工程队单独承包要120天完成.现在由甲、乙工程队合作承包,完成任务需要( )
A. 天 B. 天 C. 天 D. 天
要挖一条水渠,共有72人参加挖土和运土,已知3人挖出的土1人恰好能全部运走,怎样调动人员才能使挖出的土能及时运走 解决此问题,可设派x人挖土,其他的人运土,可列方程( )
A. B. C. D.
从甲地到乙地,公共汽车原需行驶7h,开通高速公路后,车速平均每时增加了20km,只需5h即可到达,则甲、乙两地的路程是( )
A. B. C. D.
某中学的学生军训,沿着与笔直的铁路并列的公路匀速前进,每小时走4500米,一列火车以每小时120千米的速度迎面开来,测得火车与队首学生相遇,到车尾与队末学生相遇共经过60秒,如果队伍长500米, 那么火车长( )
A. 米 B. 米 C. 米 D. 米
甲班有54人,乙班有48人,要使甲班人数是乙班的2倍,设从乙班调往甲班人数x,可列方程( )
A. B.
C. D.
请根据图中给出的信息,可得正确的方程是( )
A. B.
C. D.
在长方形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示.若设AE=x,则下列方程正确的是( )
A. B.
C. D.
二、填空题(本大题共5小题,共15分)
一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天. 如果由甲先做3天,再由这两个工程队从两端同时施工,则总共 天可以铺好这条管线.
明代大数学家程大位著的《算法统宗》一书中,记载了这样一道数学题:“八万三千短竹竿,将来要把笔头安,管三套五为期定,问郡多少能完成.”用现代的话说就是:有83000根短竹,每根短竹可制成毛笔的笔管3个或笔套5个,怎样安排制作笔管或笔套的短竹的数量,使制成的笔管与笔套正好配套 设用于制作笔管的短竹数为x根,则可列方程为 .
已知A、B两地相距1000米,甲、乙两人分别从A、B两地同时出发,沿着同一条直线公路相向而行.若甲以7米/秒的速度骑自行车前进,乙以3米/秒的速度步行,则经过 秒两人相距100米.
一列火车长240米,速度为60千米/时,一辆越野车的速度为80千米/时,当火车前进时,越野车与火车同时同向而行,由火车尾追至火车头需要__________秒.(越野车车身长不计)
某校准备组织七年级学生观看电影《我和我的祖国》,由各班班长负责买票,一班班长问售票员买团体票是否可以优惠.售票员说:“50人以上的团体票有两个优惠方案可选择,方案一:全体人员可打8折;方案二:若打9折,有6人可以免票.”
一班班长思考了一会儿,说:“我们班无论选择哪种方案要付的钱是一样的.”则一班有 人.
三、解答题(本大题共20小题,共84分)
整理一批数据,由一人做需80h完成,现在计划先由一些人做2h,再增加5人做8h,可以完成这项工作的,问怎样安排参与整理数据的具体人数?
某报社需要在40 min内将一篇紧急宣传文稿输入电脑.已知独立完成此项任务,小王需要50 min,小李需要30 min.小王独自输入了30 min后,因为急于完成任务,请求小李帮助他(求助时间忽略不计),他们能在要求的时间内完成任务吗 请说明理由.
为实施乡村振兴战略,解决某山区老百姓出行难的问题,当地政府决定修建一条高速公路.其中一段长为146 m的山体隧道贯穿工程由甲、乙两个工程队负责施工.甲工程队独立工作2天后,乙工程队加入,两工程队又联合工作了1天,这3天共掘进26 m.已知甲工程队每天比乙工程队多掘进2 m,按此速度完成这项隧道贯穿工程,甲、乙两个工程队还需联合工作多少天
在某城市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天,乙队单独完成这项工程需要90天.
(1)若由甲队先做20天,剩下的工程由甲、乙两队合作完成.甲、乙两队合作多少天
(2)甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱 还是由甲、乙两队全程合作完成该工程省钱
有一个加工茶杯的车间,一个工人每小时平均可以加工杯身12个或加工杯盖15个,车间共有90人.安排加工杯身的人数为多少时,才能使生产的杯身和杯盖正好配套
解法一:设安排加工杯身的工人为x人,则加工杯盖的工人为 人, 每小时加工杯身 个,杯盖 个,则可列方程为 .解得x= .
解法二:设共加工杯身x个(或共加工杯盖x个),则加工杯身的工人为 人,加工杯盖的工人为 人,则可列方程为 .解得x= .故加工杯身的工人为 人.
红光服装厂要生产某种型号学生服一批,已知每3米长的布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,计划用600米长的这种布料生产学生服,应分别用多少布料生产上衣和裤子,才能使上衣和裤子恰好配套?共能生产多少套?
甲、乙两地相距200 km,快车速度为120 km/h,慢车速度为80 km/h,慢车从甲地出发,快车从乙地出发,
(1)如果两车同时出发,相向而行,出发后几时两车相遇?相遇时离甲地多远?
(2)如果两车同时出发,同向(从乙开始向甲方向)而行,出发后几时两车相遇?
一轮船往返于甲、乙两码头之间,顺水航行需要3 h,逆水航行比顺水航行多用30 min,若轮船在静水中的速度为26 km/h,求水流的速度.
A,B两地间的路程为360千米,甲车从A地出发开往B地,每小时行驶72千米.甲车出发25分钟后,乙车从B地出发开往A地,每小时行驶48千米.
(1)几小时后两车相遇?
(2)两车相遇后,各自仍按原速度和原方向继续行驶.那么相遇以后两车相距100千米时,甲车从出发共行驶了多少小时?
李先生从家到公司去上班要先经过一段平路再过一段下坡路。他走平路每分钟走m,下坡路每分钟走m,上坡路每分钟走m,从家到公司需要分钟,从公司到家里需要 分钟,求李先生家离公司多远。
某中学学生步行到郊外旅行,七年级(1)班学生组成前队,步行速度为4千米/小时,七(2)班的学生组成后队,速度为6千米/小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米/小时.
(1)后队追上前队需要多长时间?
(2)后队追上前队的时间内,联络员走的路程是多少?
(3)七年级(1)班出发多少小时后两队相距2千米?
甲、乙两厂共同加工一批产品.甲厂有91名工人,乙厂有49名工人,为了赶制这批产品又调来了100名工人,要使甲厂的人数比乙厂人数的3倍少12人,应往甲、乙两厂各调多少名工人
某中学组织七年级学生去春游,原计划租用45座客车若干辆,但会有15人没有座位;如果租用同样数量的60座客车,则会多出一辆,且其余客车恰好坐满.已知45座客车日租金为每辆220元,60座客车日租金为每辆300元.问:
(1)七年级学生有多少人 按原计划需要租用45座客车多少辆
(2)要使每位学生都有座位,怎样租车更合算
一个底面直径为16厘米的圆柱形木桶内装满水,水中淹没着一个底面直径为8厘米,高为15厘米的铁质小圆柱体.当铁质小圆柱体被取出后,木桶内的水面下降了多少?
某药业集团生产的某种药品包装盒的形状是长方体,且侧面展开图如图所示.如果长方体盒子的长比宽多4 cm,求这种药品包装盒的体积.
要利用墙和篱笆为一个长方形的养鸡场(长方形的一边利用墙,三边用篱笆),现有一段长14m的墙和一段长为35m的篱笆可以利用.小王打算使围成鸡场的长比宽多5m,小赵打算使围成鸡场的长比宽多2m,你认为谁的设计符合实际?按照他的设计,鸡场的面积是多少?
在一个底面直径为5cm,高为18cm的圆柱瓶内装满水,再将瓶内的水倒入一个底面直径为6cm,高为10cm的圆柱玻璃杯中,能否完全装下 若装不下,则瓶内水还剩多高 若不能装满,求杯内水面离杯口的距离.
李老师准备购买一套小户型商品房,他去售楼处了解情况得知,该户型商品房的单价是5000元/,如图所示(单位:m,卫生间的宽未定,设宽为x m),售楼处为李老师提供了以下两种优惠方案:
方案一:整套房的单价为5000元/,其中卫生间可免费赠送一半的面积;
方案二:整套房按原销售总金额的9.5折出售.
(1)用含x的式子表示该户型商品房的面积及按方案一、方案二购买一套该户型商品房的总金额;
(2)当x=2时,通过计算说明哪种方案较优惠,优惠多少元.
为庆祝商都正式营业,商都推出了两种购物方案.
方案一:非会员购物所有商品价格可获九五折优惠;
方案二:交纳300元会员费成为该商都会员,所有商品价格可获九折优惠.
(1)以x(元)表示商品价格,分别用含有x的式子表示两种购物方案中的支出金额;
(2)若某人计划在商都购买价格为5880元的电视机一台,请分析选择哪种方案较省钱;
(3)哪种情况下,两种方案的支出金额相同
32.在“十·一”黄金周期间,某超市推出如下购物优惠方案:(1)一次性购物在100元(不含100元)以内时,不享受优惠;(2)一次性购物在100元(含100元)以上,300元(不含300元)以内时,一律享受九折的优惠;(3)一次性购物在300元(含300元)以上时,一律享受八折的优惠.王茜在本超市两次购物分别付款80元、252元.如果王茜改成在本超市一次性购买与上两次完全相同的商品,则应付款多少元?
1.【答案】A
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】A
6.【答案】A
7.【答案】B
8.【答案】
9.【答案】3x=5(83000-x)
10.【答案】 90或110
11.【答案】 43.2
12.【答案】54
13.【答案】解:设先安排x人参与整理数据,由题意得:×2+×(x+5)×8=,
解得:x=2.
答:计划先由2人整理这组数据.
14.【答案】解:能.
理由:设小李加入后,x min完成任务,
根据题意,
得+=1,解得x=7.5,
则他们完成共用时37.5 min.
因为37.5<40,
所以他们能在要求的时间内完成任务.
15.【答案】解:设甲工程队每天掘进xm,则乙工程队每天掘进(x-2)m.
由题意得2x+(x+x-2)=26
解得x=7
则乙工程队每天掘进5m
(天)
故甲乙两个工程队还需联合工作10天
16.【答案】解:(1)设甲、乙两队合作t天,
由题意得
解得:t=24.
(2)设甲、乙合作完成需y天,则有
解得,y=36,
①甲单独完成需付工程款为60×3.5=210(万元).
②乙单独完成超过计划天数不符合题意.
③甲、乙合作完成需付工程款为36×(3.5+2)=198(万元).
答:在不超过计划天数的前提下,由甲、乙合作完成最省钱.
17.【答案】解:(90-x);12x;15(90-x);12x=15(90-x);50;
;;+=90;600;50.
18.【答案】解:设用x米布料生产上衣,根据题意得:
解得:x=360,
答:用360米布料生产上衣,240米布料生产裤子,才能使上衣和裤子恰好配套。
19.【答案】 解:(1)设出发后x小时两车相遇,
由题意得:120x+80x=200,
解得:x=1,80×1=80(千米),
答:两车同时出发,相向而行,出发后1小时两车相遇;相遇时离甲地80千米;
(2)设出发后y时两车相遇,
由题意得:120y=200+80y,
解得:y=5,
答:出发后5小时两车相遇.
20.【答案】解:设水流速度为x km/h,
则船在顺水中的速度为 km/h,船在逆水中的速度为 km/h,
由题意得,,
解得,
所以水流速度为2 km/h.
21.【答案】解:(1)=330÷120
=(小时),
答:小时后两车相遇.
(2)解:设甲车从出发共行驶了x小时.
根据题意,得25分钟=小时,
72x+48(x-)=360+100,
72x+48x-20=460,
120x=480,
x=4.
答:甲车从出发共行驶4小时.
22.【答案】解:设下坡路长为米,则,
∴。
下坡时间(分钟)
平路时间(分钟)
平路长度(米)
总路程=平路长度+下坡长度 (米)
∴李先生家离公司 米。
23.【答案】解:(1)设后队追上前队需要x小时,
根据题意得:(6-4)x=4×1
∴x=2
答:后队追上前队需要2小时,
(2)10×2=20千米
答:联络员走的路程是20千米,
(3)设七年级(1)班出发t 小时后,两队相距2千米,
当七年级(2)班没有出发时,t==,
当七年级(2)班出发,但没有追上七年级(1)班时,4t=6(t-1)+2
∴t=2,
当七年级(2)班追上七年级(1)班后,6(t-1)=4t+2
∴t=4,
答:七年级(1)班出发小时或2小时或4小时后,两队相距2千米.
24.【答案】解:设应往甲厂调x名工人,则往乙厂调(100-x)名工人,
依题意,得91+x=3(49+100-x)-12.
解这个方程,得x=86.
所以100-x=14.
故应往甲厂调86名工人,往乙厂调14名工人.
25.【答案】解:(1)设原计划租用45座客车x辆,根据题意得
60(x-1)=45x+15,
解得x=5,
七年级人数是455+15=240(人),
答:七年级有学生240人,原计划租用45座客车5辆;
(2)租45座客车:240÷45≈5.3(辆),
所以需租6辆,租金为220×6=1320(元),
租60座客车:240÷60=4(辆),
所以需租4辆,租金为300×4=1200(元),
租45座客车4辆,租金:220×4=880元,
租60座客车1辆,租金:300元,
880+300=1180<1200<1320,
答:租用4辆45座客车租1辆60座客车更合算.
26.【答案】解:设当小圆柱体取出后,木桶内水面降低xcm,根据题意可得:
π×42×15=π×82x,
解得:x=.
答:木桶内的水面下降了厘米.
27.【答案】解:这种药品包装盒的体积为.
28.【答案】解: 设宽为xm,根据小王的方案可列方程
2x+x+5=35,解得x=10
所以x+5=15>14,所以这个方案不符合实际.
根据小王的方案可列方程2x+x+2=35,
解得x=11所以x+2=13<14,
所以这个方案符合实际,其面积为11×13=143(m2).
答:小赵的方案符合实际,其面积为11×13=143(m2).
29.【答案】解:根据题意得
圆柱形瓶内的体积为=,
圆柱形玻璃杯的体积为=,
因为,
故不能装下.
将圆柱形玻璃杯的水装满后,圆柱形瓶内水
的体积还有:,
故瓶中还剩水的高度为:.
30.【答案】解:(1)该户型商品房的面积为47+3(8-4)+2(7-3)+(8-4-2)x=48+2x().
该户型商品房的卫生间面积为(8-4-2)x=2x().
按方案一购买一套该户型商品房的总金额为5000=240000+5000x(元);
按方案二购买一套该户型商品房的总金额为(48+2x)500095%=228000+9500x(元).
(2)当x=2时,方案一总金额为240000+5000x=250000(元);
方案二总金额为228000+9500x=247000(元).
方案二比方案一优惠250000-247000=3000(元).
所以方案二较优惠,优惠3000元.
31.【答案】解:(1)方案一:0.95x元,
方案二:(0.9x+300)元;
(2)当x=5880时,
方案一支出金额为0.955880=5586(元),
方案二支出金额为0.95880+300=5592(元).
因为5592元>5586元,
所以选择方案一较省钱;
(3)由题意,得0.95x=0.9x+300,解得x=6000.
答:当商品价格是6000元时,两种方案的支出金额相同.
32.【答案】解:设应付款x元.
(1)若第2次购物没有超过300元,根据题意,得
x÷ =80+252÷,
解得,x=288(元),
(2)若第2次购物超过300元,根据题意,得
x÷ =80+252÷,
解得,x=316元),
答:王茜改成在本超市一次性购买与上两次完全相同的商品,则应付款288元或316元.
第2页,共2页
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
