2021-2022学年沪科版七年级数学上册第四章直线与角同步测试卷-(word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版七年级数学上册第四章直线与角同步测试卷-(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 250.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 23:08:47 | ||
图片预览



文档简介
第四章直线与角同步测试卷 2021-2022学年沪科版七年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
A. B.
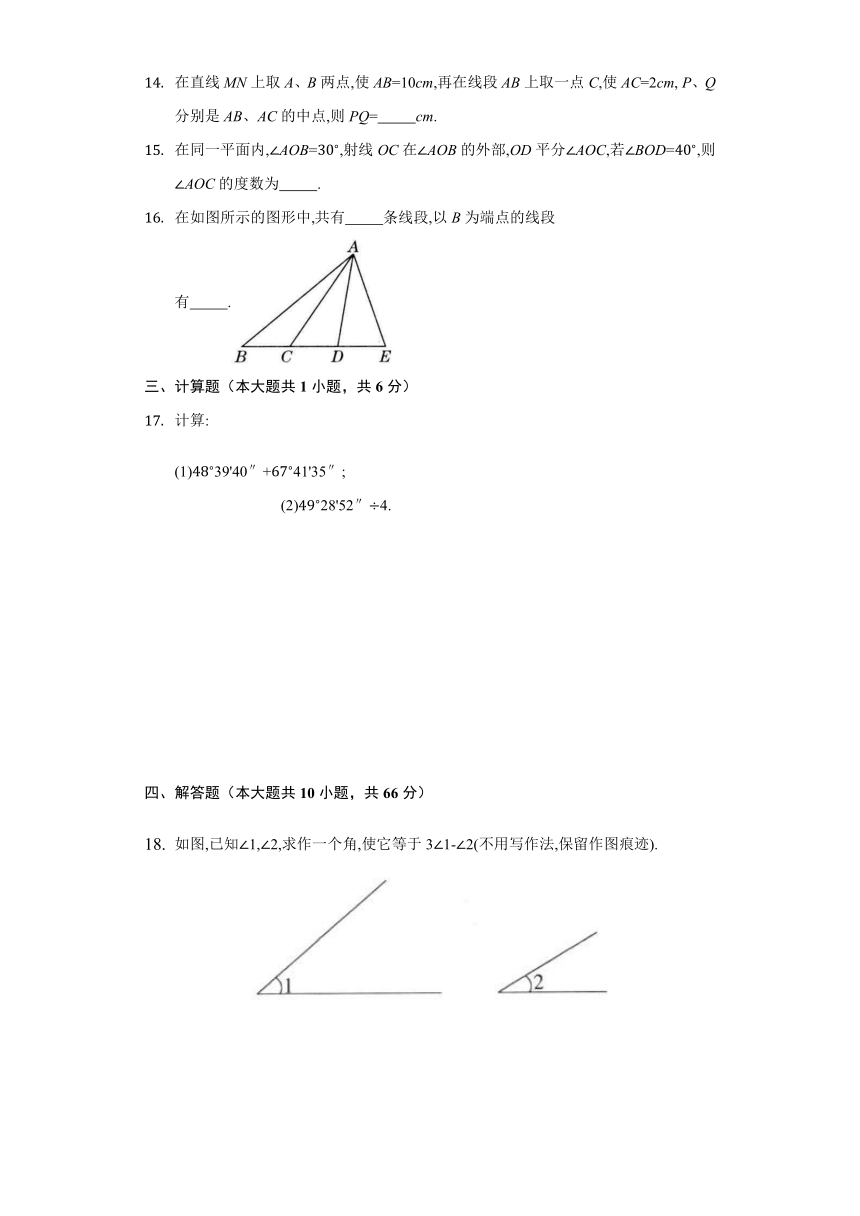
C. D.
如图,A,B,C 三个车站在东西方向笔直的一条公路上,现要建一个加油站使其到三个车站的距离和最小,则加油站应建在( )
A. 的左侧 B. ,之间 C. ,之间 D. 处
若=29°45',则的余角等于( )
A. B. C. D.
将16.38°用度、分、秒表示,结果是( )
A. B. C. D.
如图,下列关于图中线段之间的关系一定正确的是( )
A. B.
C. D.
如图,AOC为直角,OC是BOD的平分线,且AOB=,则AOD的度数为( )
A. B.
C. D.
已知线段AB,画出它的中点C,再画出BC的中点D,再画出AD的中点E,再画出AE的中点F,那么AF等于AB的( )
A. B. C. D.
如果与互余,且,那么下列表示的补角的式子中,-,+,2+,2+,正确的是( )
A. B. C. D.
如图,B,C 两点把线段 MN 分成三部分,其比为MB : BC : CN=2 : 3 : 4,点 P 是 MN 的中点,PC=2 cm,则 MN 的长为( )
A. B. C. D.
某初中数学名师工作室积极开展“名师送教”活动.其中,成员卢老师在一次送教课上,利用多媒体展示如下内容:C 为直线 AB 上一点(如图),DCE 为直角,CF平分ACD,CH平分BCD,CG平分BCE,各个小组经过讨论后得到以下结论:ACF与BCH 互余;FCG与HCG 互补;ECF 与GCH 互补;ACD-BCE=,聪明的你认为哪些组的结论是正确的,正确的个数有( )
A. B. C. D.
二、填空题(本大题共6小题,共18分)
已知与互为余角,=40',则= .
画线段AB=1cm,延长线段AB到C,使线段BC= 2 cm,已知点D是线段BC的中点,则线段AD= cm.
如图,将一副三角板叠放在一起,使直角的顶点重合于O,若AOC=,则DOB= .
在直线MN上取A、B两点,使AB=10cm,再在线段AB上取一点C,使AC=2cm, P、Q分别是AB、AC的中点,则PQ= cm.
在同一平面内,AOB=,射线OC在AOB的外部,OD平分AOC,若BOD=,则AOC的度数为 .
在如图所示的图形中,共有 条线段,以B为端点的线段有 .
三、计算题(本大题共1小题,共6分)
计算:
(1)39'40″+41'35″;
(2)28'52″4.
四、解答题(本大题共10小题,共66分)
如图,已知1,2,求作一个角,使它等于31-2(不用写作法,保留作图痕迹).
如图,点C在线段AB上,AC=6cm, MB=10cm,点M、N分别为AC、BC的中点.
(1)求线段BC、MN的长;
(2)若C在线段AB的延长线上,且满足AC-BC= bcm,M、N分别是线段AC、BC的中点,求MN的长度.
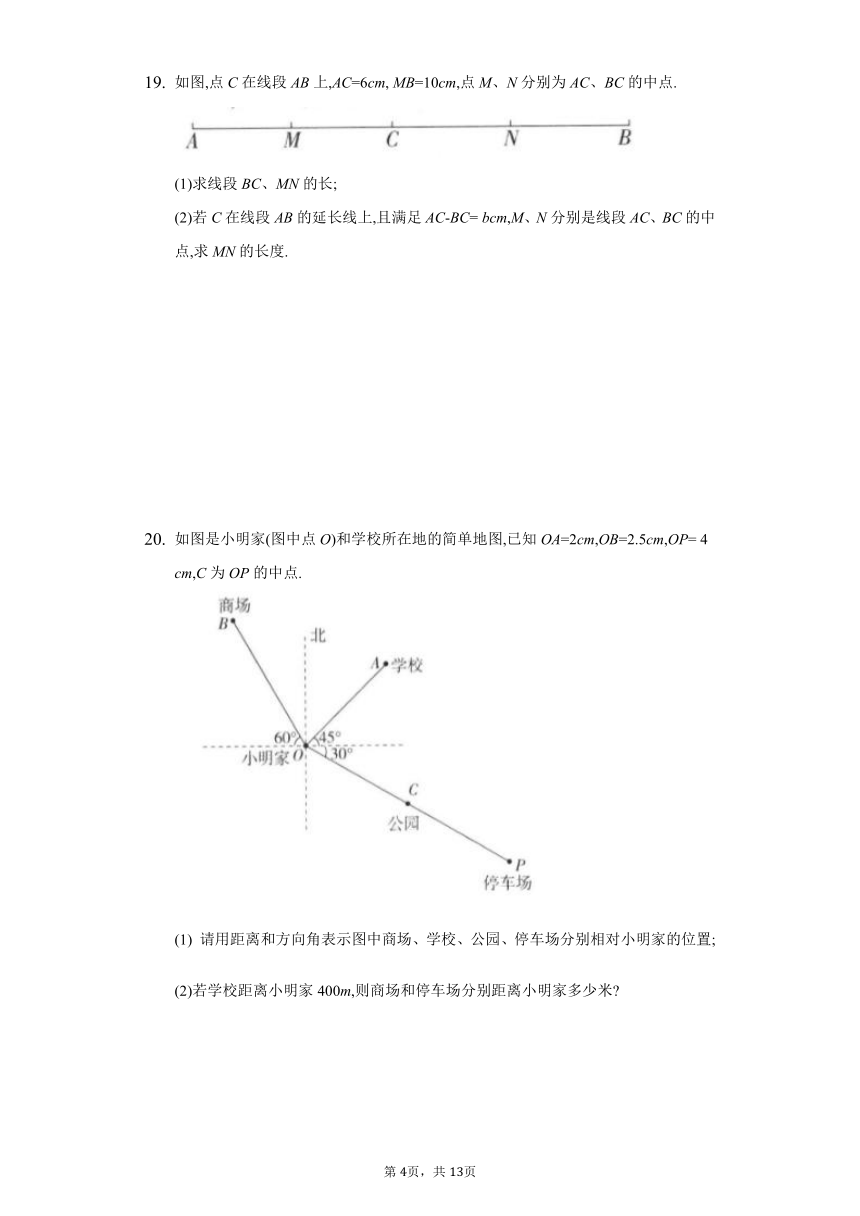
如图是小明家(图中点O)和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP= 4 cm,C为OP的中点.
(1) 请用距离和方向角表示图中商场、学校、公园、停车场分别相对小明家的位置;
(2)若学校距离小明家400m,则商场和停车场分别距离小明家多少米
如图,已知线段AB上顺次有三个点C、D、E,它们把线段AB分成2:3:4:5四部分,且AB=56cm.
(1)求线段AE的长;
(2)若M、N分别是DE、EB的中点,求线段MN的长度.
把一副三角板拼在一起,如图所示.
(1)写出图中A、B、BCD、D、AED的度数;
(2)用“<”将上述各角按度数大小连接起来.
如图所示,请按照要求解答问题.
(1)数轴上的点C在2,3的正中间位置,则点C表示的数是 ,线段AB的中点D表示的数是 ;
(2)线段AB的中点D与线段BC的中点E的距离为 ;
(3)在数轴上方有一点M,下方有一点N,且ABM=,CBN=,请画出示意图,并判断BC是否平分MBN.简要说明理由.
(1)如图,直线上有2个点,则图中有2条可用图中字母表示的射线,有1条线段;
(2)如图,直线上有3个点,则图中有 条可用图中字母表示的射线,有 条线段;
(3)如图,直线上有n个点,则图中有 条可用图中字母表示的射线,有 条线段;
(4)应用(3)中发现的规律解决问题:某校七年级共有6个班进行足球比赛,准备进行循环赛(即每两队之间赛一场),预计全部赛完共需 场比赛.
(1)试验观察:
如图,经过平面上不在同一直线上的三个点,最多可以画 条直线;
如图,经过平面上不在同一直线上的四个点,最多可以画 条直线;
如图,经过平面上不在同一直线上的五个点,最多可以画 条直线.
(2)探索归纳:
如果平面上有n(n3)个点,且没有3个点在同一直线上,那么经过这些点最多可以画 条直线(用含n的式子表示).
为了探究同一平面内的几条直线相交最多能产生多少个交点,能把平面最多分成多少部分,我们从最简单的情形入手,如图所示.
列表如下:
直线条数 最多交点的个数 把平面最多分成的部分数
1 0 2
2 1 4
3 3 7
(1)当直线条数为5时,最多有 个交点,可写成和的形式为 ;把平面最多分成 部分,可写成和的形式为 ;
(2)当直线条数为10时,最多有 个交点,把平面最多分成 部分;
(3)当直线条数为n时,最多有多少个交点 把平面最多分成多少部分
有公共端点的两条射线组成的图形叫做角,这个公共端点叫做角的顶点.
如果以角的顶点A为端点,
(1)如图,在角的内部作一条射线,那么图中一共有几个角
(2)如图,在角的内部作两条射线,那么图中一共有几个角
(3)如图,在角的内部作三条射线,那么图中一共有几个角
(4)在角的内部作n条射线,那么一共有几个角
1.【答案】B
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】D
8.【答案】B
9.【答案】B
10.【答案】C
11.【答案】
12.【答案】2
13.【答案】
14.【答案】 4
15.【答案】或
16.【答案】10
AB,BC,BD,BE
17.【答案】解:(1)39'40″+41'35″=80'75″=21'15″.
(2)28'52″4=+88'52″4=22'+52″4=22'13″.
18.【答案】解:如图:
(1)以1 的顶点 O 为圆心,以适当的长为半径画弧,分别交1 的两边 OA、OB 于点 E、F;
(2)在弧上利用圆规依次取点G、H,使 FG=GH=EF;
(3)自 O 点过 H 点作射线 OD,则AOD 即为3 1;
(4)以2 的顶点为圆心,适当长为半径画弧交2 的两边于M'、N'两点;
(5)以 O 为圆心,以同样长为半径画弧交 OA 于点 M;
(6)以 M 为圆心,以 M'N' 的长为半径画弧交前弧于点 N;
(7)自 O 点过 N 点作射线 OC.COD 即为所求.
19.【答案】解:(1)因为AC=6cm,M是AC的中点,
所以AM=MC=AC=3cm.
因为MB=10cm,
所以BC=MB-MC=7cm.
因为N为BC的中点,
所以CN=BC=3.5cm,
所以MN=MC+CN=6.5cm.
(2)如图,
因为M是AC的中点,N是BC的中点,
所以MC=AC,NC=BC.
因为AC-BC=bcm,
所以MN=MC-NC=AC-BC=(AC-BC)=b(cm).
20.【答案】解:(1)商场在小明家北偏西方向,距离2.5cm的位置;
学校在小明家东北方向,距离2cm的位置;
公园在小明家南偏东方向,距离2cm的位置;
停车场在小明家南偏东方向,距离4cm的位置.
(2)因为学校距离小明家400m,且OA=2cm,所以图中1cm表示200m,
所以商场距离小明家2.5200=500m,停车场距离小明家4200=800m.
21.【答案】解:(1)设AC=2xcm,则CD、DE、EB的长度分别为3xcm、4xcm、5xcm,
由题意得,2x+3x+4x+5x=56,
解得x=4,
则AC、CD、DE、EB的长度分别为8cm、12cm、16cm、20cm,
所以AE=AC+CD+DE=36cm.
(2)因为M是DE的中点,所以ME=DE=8cm.
因为N是EB的中点,所以EN=EB=10cm,
所以MN=ME+EN=18cm.
22.【答案】解:(1)A=,B=,BCD=+=,D=,
AED=-=.
(2)A23.【答案】解:(1)2.5;-2.
(2)2.75.
(3)示意图如图.
BC平分MBN.
理由:因为ABM=,所以MBC=-ABM=-=.
又因为CBN=,所以MBC=CBN,即BC平分MBN.
24.【答案】解:(2)4;3 (3)(2n-2); (4)15
25.【答案】(1)3 6 10
(2)
26.【答案】解:(1)10;1+2+3+4;16;1+1+2+3+4+5
(2)45;56
(3)当直线条数为n时,
最多有1+2+3++(n-1)=(个)交点,
把平面最多分成1+1+2+3++n=部分.
27.【答案】解:(1)如题图,已知BAC,如果在其内部作一条射线,显然这条射线就会和BAC的两条边都组成一个角,这样一共就有1+2=3(个)角.
(2)题图有1+2=3(个)角,如果再在题图的角的内部增加一条射线,即为题图,显然这条射线就会和图原来的三条射线再组成三个角,即题图共有1+2+3=6(个)角.
(3)如题图,在角的内部作三条射线,即在题图的角的内部再增加一条射线,同样这条射线就会和图原来的四条射线再组成四个角,即题图共有1+2+3+4=10(个)角.
(4)如果在一个角的内部作n条射线,则共有1+2+3++n+(n+1)=(个)角.
第2页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
A. B.
C. D.
如图,A,B,C 三个车站在东西方向笔直的一条公路上,现要建一个加油站使其到三个车站的距离和最小,则加油站应建在( )
A. 的左侧 B. ,之间 C. ,之间 D. 处
若=29°45',则的余角等于( )
A. B. C. D.
将16.38°用度、分、秒表示,结果是( )
A. B. C. D.
如图,下列关于图中线段之间的关系一定正确的是( )
A. B.
C. D.
如图,AOC为直角,OC是BOD的平分线,且AOB=,则AOD的度数为( )
A. B.
C. D.
已知线段AB,画出它的中点C,再画出BC的中点D,再画出AD的中点E,再画出AE的中点F,那么AF等于AB的( )
A. B. C. D.
如果与互余,且,那么下列表示的补角的式子中,-,+,2+,2+,正确的是( )
A. B. C. D.
如图,B,C 两点把线段 MN 分成三部分,其比为MB : BC : CN=2 : 3 : 4,点 P 是 MN 的中点,PC=2 cm,则 MN 的长为( )
A. B. C. D.
某初中数学名师工作室积极开展“名师送教”活动.其中,成员卢老师在一次送教课上,利用多媒体展示如下内容:C 为直线 AB 上一点(如图),DCE 为直角,CF平分ACD,CH平分BCD,CG平分BCE,各个小组经过讨论后得到以下结论:ACF与BCH 互余;FCG与HCG 互补;ECF 与GCH 互补;ACD-BCE=,聪明的你认为哪些组的结论是正确的,正确的个数有( )
A. B. C. D.
二、填空题(本大题共6小题,共18分)
已知与互为余角,=40',则= .
画线段AB=1cm,延长线段AB到C,使线段BC= 2 cm,已知点D是线段BC的中点,则线段AD= cm.
如图,将一副三角板叠放在一起,使直角的顶点重合于O,若AOC=,则DOB= .
在直线MN上取A、B两点,使AB=10cm,再在线段AB上取一点C,使AC=2cm, P、Q分别是AB、AC的中点,则PQ= cm.
在同一平面内,AOB=,射线OC在AOB的外部,OD平分AOC,若BOD=,则AOC的度数为 .
在如图所示的图形中,共有 条线段,以B为端点的线段有 .
三、计算题(本大题共1小题,共6分)
计算:
(1)39'40″+41'35″;
(2)28'52″4.
四、解答题(本大题共10小题,共66分)
如图,已知1,2,求作一个角,使它等于31-2(不用写作法,保留作图痕迹).
如图,点C在线段AB上,AC=6cm, MB=10cm,点M、N分别为AC、BC的中点.
(1)求线段BC、MN的长;
(2)若C在线段AB的延长线上,且满足AC-BC= bcm,M、N分别是线段AC、BC的中点,求MN的长度.
如图是小明家(图中点O)和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP= 4 cm,C为OP的中点.
(1) 请用距离和方向角表示图中商场、学校、公园、停车场分别相对小明家的位置;
(2)若学校距离小明家400m,则商场和停车场分别距离小明家多少米
如图,已知线段AB上顺次有三个点C、D、E,它们把线段AB分成2:3:4:5四部分,且AB=56cm.
(1)求线段AE的长;
(2)若M、N分别是DE、EB的中点,求线段MN的长度.
把一副三角板拼在一起,如图所示.
(1)写出图中A、B、BCD、D、AED的度数;
(2)用“<”将上述各角按度数大小连接起来.
如图所示,请按照要求解答问题.
(1)数轴上的点C在2,3的正中间位置,则点C表示的数是 ,线段AB的中点D表示的数是 ;
(2)线段AB的中点D与线段BC的中点E的距离为 ;
(3)在数轴上方有一点M,下方有一点N,且ABM=,CBN=,请画出示意图,并判断BC是否平分MBN.简要说明理由.
(1)如图,直线上有2个点,则图中有2条可用图中字母表示的射线,有1条线段;
(2)如图,直线上有3个点,则图中有 条可用图中字母表示的射线,有 条线段;
(3)如图,直线上有n个点,则图中有 条可用图中字母表示的射线,有 条线段;
(4)应用(3)中发现的规律解决问题:某校七年级共有6个班进行足球比赛,准备进行循环赛(即每两队之间赛一场),预计全部赛完共需 场比赛.
(1)试验观察:
如图,经过平面上不在同一直线上的三个点,最多可以画 条直线;
如图,经过平面上不在同一直线上的四个点,最多可以画 条直线;
如图,经过平面上不在同一直线上的五个点,最多可以画 条直线.
(2)探索归纳:
如果平面上有n(n3)个点,且没有3个点在同一直线上,那么经过这些点最多可以画 条直线(用含n的式子表示).
为了探究同一平面内的几条直线相交最多能产生多少个交点,能把平面最多分成多少部分,我们从最简单的情形入手,如图所示.
列表如下:
直线条数 最多交点的个数 把平面最多分成的部分数
1 0 2
2 1 4
3 3 7
(1)当直线条数为5时,最多有 个交点,可写成和的形式为 ;把平面最多分成 部分,可写成和的形式为 ;
(2)当直线条数为10时,最多有 个交点,把平面最多分成 部分;
(3)当直线条数为n时,最多有多少个交点 把平面最多分成多少部分
有公共端点的两条射线组成的图形叫做角,这个公共端点叫做角的顶点.
如果以角的顶点A为端点,
(1)如图,在角的内部作一条射线,那么图中一共有几个角
(2)如图,在角的内部作两条射线,那么图中一共有几个角
(3)如图,在角的内部作三条射线,那么图中一共有几个角
(4)在角的内部作n条射线,那么一共有几个角
1.【答案】B
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】D
8.【答案】B
9.【答案】B
10.【答案】C
11.【答案】
12.【答案】2
13.【答案】
14.【答案】 4
15.【答案】或
16.【答案】10
AB,BC,BD,BE
17.【答案】解:(1)39'40″+41'35″=80'75″=21'15″.
(2)28'52″4=+88'52″4=22'+52″4=22'13″.
18.【答案】解:如图:
(1)以1 的顶点 O 为圆心,以适当的长为半径画弧,分别交1 的两边 OA、OB 于点 E、F;
(2)在弧上利用圆规依次取点G、H,使 FG=GH=EF;
(3)自 O 点过 H 点作射线 OD,则AOD 即为3 1;
(4)以2 的顶点为圆心,适当长为半径画弧交2 的两边于M'、N'两点;
(5)以 O 为圆心,以同样长为半径画弧交 OA 于点 M;
(6)以 M 为圆心,以 M'N' 的长为半径画弧交前弧于点 N;
(7)自 O 点过 N 点作射线 OC.COD 即为所求.
19.【答案】解:(1)因为AC=6cm,M是AC的中点,
所以AM=MC=AC=3cm.
因为MB=10cm,
所以BC=MB-MC=7cm.
因为N为BC的中点,
所以CN=BC=3.5cm,
所以MN=MC+CN=6.5cm.
(2)如图,
因为M是AC的中点,N是BC的中点,
所以MC=AC,NC=BC.
因为AC-BC=bcm,
所以MN=MC-NC=AC-BC=(AC-BC)=b(cm).
20.【答案】解:(1)商场在小明家北偏西方向,距离2.5cm的位置;
学校在小明家东北方向,距离2cm的位置;
公园在小明家南偏东方向,距离2cm的位置;
停车场在小明家南偏东方向,距离4cm的位置.
(2)因为学校距离小明家400m,且OA=2cm,所以图中1cm表示200m,
所以商场距离小明家2.5200=500m,停车场距离小明家4200=800m.
21.【答案】解:(1)设AC=2xcm,则CD、DE、EB的长度分别为3xcm、4xcm、5xcm,
由题意得,2x+3x+4x+5x=56,
解得x=4,
则AC、CD、DE、EB的长度分别为8cm、12cm、16cm、20cm,
所以AE=AC+CD+DE=36cm.
(2)因为M是DE的中点,所以ME=DE=8cm.
因为N是EB的中点,所以EN=EB=10cm,
所以MN=ME+EN=18cm.
22.【答案】解:(1)A=,B=,BCD=+=,D=,
AED=-=.
(2)A
(2)2.75.
(3)示意图如图.
BC平分MBN.
理由:因为ABM=,所以MBC=-ABM=-=.
又因为CBN=,所以MBC=CBN,即BC平分MBN.
24.【答案】解:(2)4;3 (3)(2n-2); (4)15
25.【答案】(1)3 6 10
(2)
26.【答案】解:(1)10;1+2+3+4;16;1+1+2+3+4+5
(2)45;56
(3)当直线条数为n时,
最多有1+2+3++(n-1)=(个)交点,
把平面最多分成1+1+2+3++n=部分.
27.【答案】解:(1)如题图,已知BAC,如果在其内部作一条射线,显然这条射线就会和BAC的两条边都组成一个角,这样一共就有1+2=3(个)角.
(2)题图有1+2=3(个)角,如果再在题图的角的内部增加一条射线,即为题图,显然这条射线就会和图原来的三条射线再组成三个角,即题图共有1+2+3=6(个)角.
(3)如题图,在角的内部作三条射线,即在题图的角的内部再增加一条射线,同样这条射线就会和图原来的四条射线再组成四个角,即题图共有1+2+3+4=10(个)角.
(4)如果在一个角的内部作n条射线,则共有1+2+3++n+(n+1)=(个)角.
第2页,共3页
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
