湘教版七年级数学上册 名校优选精练 第四章 图形的认识 单元检测题(含答案)
文档属性
| 名称 | 湘教版七年级数学上册 名校优选精练 第四章 图形的认识 单元检测题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 00:00:00 | ||
图片预览




文档简介
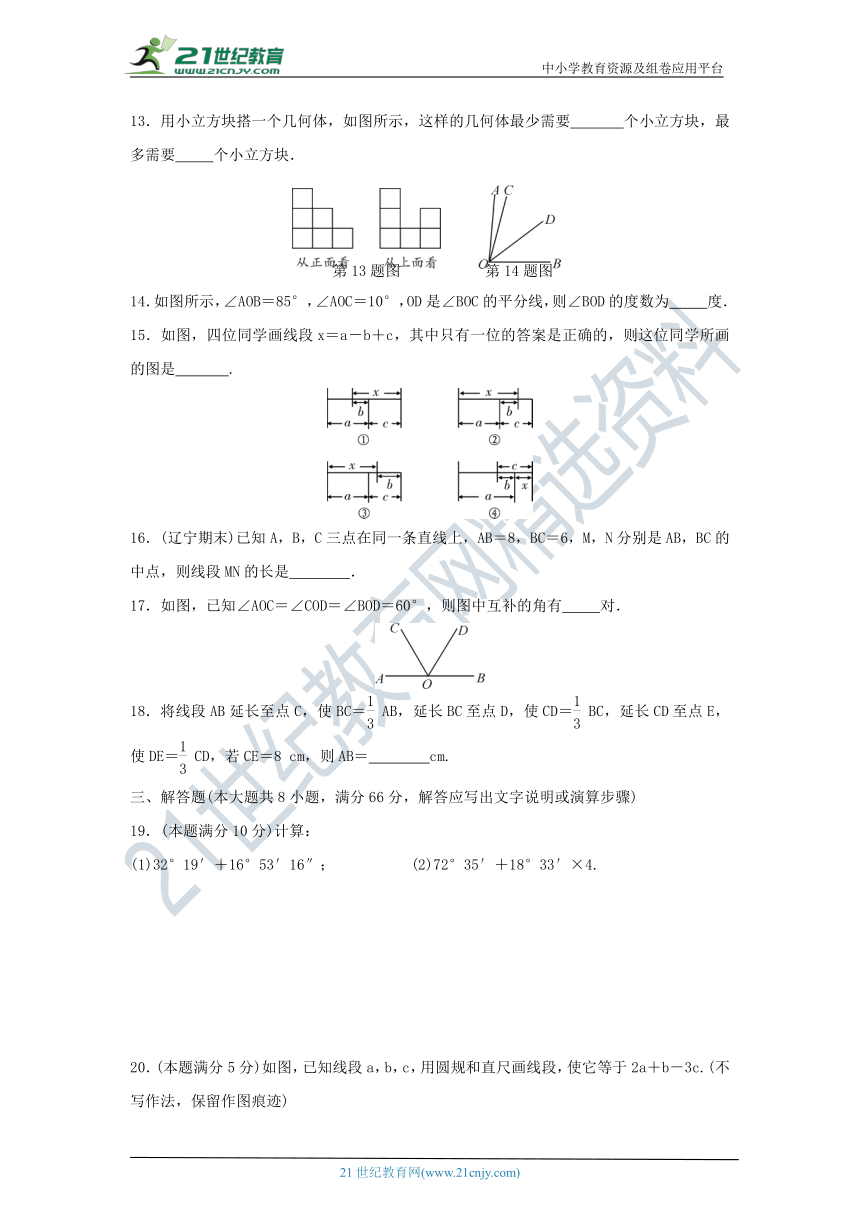
中小学教育资源及组卷应用平台
湘教版七年级数学上册 名校优选精练 第四章检测题
班级:________姓名:________考号:________
(本试卷分第Ⅰ卷和第Ⅱ卷,考试时间:120分钟,赋分:120分)
第Ⅰ卷(选择题 共36分)
一、选择题(本大题共12小题,每小题3分,共36分)
1.下面四个图形中,是三棱柱的平面展开图的是( )
eq \o(\s\up7(),\s\do5(A)) eq \o(\s\up7(),\s\do5(B)) eq \o(\s\up7(),\s\do5(C)) eq \o(\s\up7(),\s\do5(D))
2.下列画图的语句中,正确的是( )
A.画直线AB=10 cm B.画射线OB=10 cm
C.延长射线BA到C,使BA=BC D.画线段CD=2 cm
3.如图,小亮为将一个衣架固定在墙上,他在衣架两端各用一个钉子进行固定,用数学知识解释他这样操作的原因,应该是( )
A.过一点有无数条直线
B.两点之间线段的长度,叫做这两点之间的距离
C.经过两点有且只有一条直线
D.两点之间,线段最短
4.不能用一副三角板画出的角是( )
A.15° B.75° C.105° D.125°
5.54.27°用度、分、秒表示为( )
A.54°16′26″ B.54°28′ C.54°16′15″ D.54°16′12″
6.如图,已知线段AB=18 cm,M为AB的中点,点C在线段AB上且CB=AB,则线段MC的长为( )
A.1 cm B.2 cm C.3 cm D.4 cm
7.(江西期末)若将一副三角板按如图所示的不同方式摆放,则图中∠α与∠β相等的是( )
eq \o(\s\up7(),\s\do5(A)) eq \o(\s\up7(),\s\do5(B)) eq \o(\s\up7(),\s\do5(C)) eq \o(\s\up7(),\s\do5(D))
8.当钟表的时间为10 ∶30时,时针与分针的夹角是( )
A.95° B.125° C.135° D.145°
9.如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠AOD=104°,则∠BOM等于( )
A.144° B.142° C.104° D.38°
第9题图 第10题图
10.(江苏期末)如图,该表面展开图按虚线折叠成正方体后,相对面上的两个数互为相反数,则(x+y)的值为( )
A.-2 B.-3 C.2 D.1
11.(河北期末)如图,下列关于图中线段之间的关系一定正确的是( )
A.x=2a+2b-c B.c-b=2a-2b
C.x+b=2a+c-b D.x+2a=3c+2b
12.如图所示,以O为端点画六条射线OA,OB,OC,OD,OE,OF后,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线上所描的点依次记为1,2,3,4,5,6,7,8,…,那么所描的第2 021个点在射线( )
A.OE上B.OF上C.OA上D.OB上
第Ⅱ卷(非选择题 共84分)
二、填空题(本大题共6小题,每小题3分,共18分)
13.用小立方块搭一个几何体,如图所示,这样的几何体最少需要 个小立方块,最多需要 个小立方块.
eq \o(\s\up7(),\s\do5(第13题图)) eq \o(\s\up7(),\s\do5(第14题图))
14.如图所示,∠AOB=85°,∠AOC=10°,OD是∠BOC的平分线,则∠BOD的度数为 度.
15.如图,四位同学画线段x=a-b+c,其中只有一位的答案是正确的,则这位同学所画的图是 .
16.(辽宁期末)已知A,B,C三点在同一条直线上,AB=8,BC=6,M,N分别是AB,BC的中点,则线段MN的长是 .
17.如图,已知∠AOC=∠COD=∠BOD=60°,则图中互补的角有 对.
将线段AB延长至点C,使BC=AB,延长BC至点D,使CD=BC,延长CD至点E,使DE=CD,若CE=8 cm,则AB= cm.
三、解答题(本大题共8小题,满分66分,解答应写出文字说明或演算步骤)
19.(本题满分10分)计算:
(1)32°19′+16°53′16″; (2)72°35′+18°33′×4.
20.(本题满分5分)如图,已知线段a,b,c,用圆规和直尺画线段,使它等于2a+b-3c.(不写作法,保留作图痕迹)
21.(本题满分6分)一个角的补角比它的余角的3倍少30°,求这个角和它的余角.
22.(本题满分8分)如图,O在直线AC上,OD是∠AOB的平分线,OE在∠BOC内.
(1)若OE是∠BOC的平分线,则有∠DOE=90°,试说明理由;
(2)若∠BOE=∠EOC,∠DOE=72°,求∠EOC的度数.
23.(本题满分8分)如图所示,B,C两点把线段AD分成4∶5∶7三部分,点E是线段AD的中点,CD=14 cm,求:
(1)EC的长; (2)AB ∶BE的值.
24.(本题满分8分)(湖北期末)如图,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)若∠AOB=40°,∠DOE=30°,求∠BOD的度数;
(2)若∠AOD与∠BOD互补,且∠DOE=35°,求∠AOC的度数.
25.(本题满分11分)在直线l上任取一点A,截取AB=16 cm,再截取AC=40 cm,求AB的中点D与AC的中点E之间的距离.
26.(本题满分10分)(辽宁期末)【阅读】小白遇到这样一个问题:
如图,点C是线段AB的中点,AD=DB,CD=10,求AB的长.
eq \o(\s\up7(),\s\do5(①))
小白的思路是:设AB=x,根据“CD=10”列方程,请按照小白的思路完成此问题的解答.
【解决问题】用学过的知识或参考小白的方法,解决下面的问题:
已知OC,OD是∠AOB的内部的两条射线,∠AOC=∠AOB,∠AOD=m∠DOB,∠COD=n°.
(1)如图②,若m=,n=22,求∠DOB的度数;
(2)如图③,若n=14(3-2m)求∠DOB的度数.
eq \o(\s\up7(),\s\do5(②)) eq \o(\s\up7(),\s\do5(③))
参考答案
第Ⅰ卷(选择题 共36分)
一、选择题(本大题共12小题,每小题3分,共36分)
1.下面四个图形中,是三棱柱的平面展开图的是(C)
eq \o(\s\up7(),\s\do5(A)) eq \o(\s\up7(),\s\do5(B)) eq \o(\s\up7(),\s\do5(C)) eq \o(\s\up7(),\s\do5(D))
2.下列画图的语句中,正确的是(D)
A.画直线AB=10 cm B.画射线OB=10 cm
C.延长射线BA到C,使BA=BC D.画线段CD=2 cm
3.如图,小亮为将一个衣架固定在墙上,他在衣架两端各用一个钉子进行固定,用数学知识解释他这样操作的原因,应该是(C)
A.过一点有无数条直线
B.两点之间线段的长度,叫做这两点之间的距离
C.经过两点有且只有一条直线
D.两点之间,线段最短
4.不能用一副三角板画出的角是(D)
A.15° B.75° C.105° D.125°
5.54.27°用度、分、秒表示为(D)
A.54°16′26″ B.54°28′ C.54°16′15″ D.54°16′12″
6.如图,已知线段AB=18 cm,M为AB的中点,点C在线段AB上且CB=AB,则线段MC的长为(C)
A.1 cm B.2 cm C.3 cm D.4 cm
7.(江西期末)若将一副三角板按如图所示的不同方式摆放,则图中∠α与∠β相等的是(A)
eq \o(\s\up7(),\s\do5(A)) eq \o(\s\up7(),\s\do5(B)) eq \o(\s\up7(),\s\do5(C)) eq \o(\s\up7(),\s\do5(D))
8.当钟表的时间为10 ∶30时,时针与分针的夹角是(C)
A.95° B.125° C.135° D.145°
9.如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠AOD=104°,则∠BOM等于(B)
A.144° B.142° C.104° D.38°
第9题图 第10题图
10.(江苏期末)如图,该表面展开图按虚线折叠成正方体后,相对面上的两个数互为相反数,则(x+y)的值为(C)
A.-2 B.-3 C.2 D.1
11.(河北期末)如图,下列关于图中线段之间的关系一定正确的是(C)
A.x=2a+2b-c B.c-b=2a-2b
C.x+b=2a+c-b D.x+2a=3c+2b
12.如图所示,以O为端点画六条射线OA,OB,OC,OD,OE,OF后,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线上所描的点依次记为1,2,3,4,5,6,7,8,…,那么所描的第2 021个点在射线(A)
A.OE上B.OF上C.OA上D.OB上
第Ⅱ卷(非选择题 共84分)
二、填空题(本大题共6小题,每小题3分,共18分)
13.用小立方块搭一个几何体,如图所示,这样的几何体最少需要9个小立方块,最多需要13个小立方块.
eq \o(\s\up7(),\s\do5(第13题图)) eq \o(\s\up7(),\s\do5(第14题图))
14.如图所示,∠AOB=85°,∠AOC=10°,OD是∠BOC的平分线,则∠BOD的度数为37.5度.
15.如图,四位同学画线段x=a-b+c,其中只有一位的答案是正确的,则这位同学所画的图是③.
16.(辽宁期末)已知A,B,C三点在同一条直线上,AB=8,BC=6,M,N分别是AB,BC的中点,则线段MN的长是1或7.
17.如图,已知∠AOC=∠COD=∠BOD=60°,
则图中互补的角有6对.
将线段AB延长至点C,使BC=AB,延长BC至点D,使CD=BC,延长CD至点E,使DE=CD,若CE=8 cm,
则AB=54cm.
三、解答题(本大题共8小题,满分66分,解答应写出文字说明或演算步骤)
19.(本题满分10分)计算:
(1)32°19′+16°53′16″;
解:32°19′+16°53′16″=49°12′16″.
(2)72°35′+18°33′×4.
解:72°35′+18°33′×4
=72°35′+72°132′
=72°35′+74°12′
=146°47′.
20.(本题满分5分)如图,已知线段a,b,c,用圆规和直尺画线段,使它等于2a+b-3c.(不写作法,保留作图痕迹)
解:作图略.
21.(本题满分6分)一个角的补角比它的余角的3倍少30°,求这个角和它的余角.
解:设这个角为x°,
则3(90-x)-30=180-x,
解得x=30,
所以90°-30°=60°.
答:这个角为30°,它的余角为60°.
22.(本题满分8分)如图,O在直线AC上,OD是∠AOB的平分线,OE在∠BOC内.
(1)若OE是∠BOC的平分线,则有∠DOE=90°,试说明理由;
(2)若∠BOE=∠EOC,∠DOE=72°,求∠EOC的度数.
解:(1)因为OD是∠AOB的平分线,OE是∠BOC的平分线,
所以∠BOD=∠AOB,∠BOE=∠BOC,
所以∠DOE=(∠AOB+∠BOC)
=∠AOC=90°.
(2)设∠EOB=x,则∠EOC=2x,
则∠BOD=(180°-3x),
则∠BOE+∠BOD=∠DOE,
即x+(180°-3x)=72°,
解得x=36°,
故∠EOC=2x=72°.
23.(本题满分8分)如图所示,B,C两点把线段AD分成4∶5∶7三部分,点E是线段AD的中点,CD=14 cm,求:
(1)EC的长;
解:设线段AB,BC,CD分别为4x cm,5x cm,7x cm,
则∵CD=7x=14,∴x=2.
∵AB=4x=8 cm,BC=5x=10 cm,
∴AD=AB+BC+CD=8+10+14=32 cm,
故EC=AD-CD=×32-14=2 cm.
(2)AB ∶BE的值.
解:∵BC=10 cm,EC=2 cm,
∴BE=BC-EC=10-2=8 cm,
又∵AB=8 cm,
∴AB∶ BE=8∶8=1.
24.(本题满分8分)(湖北期末)如图,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)若∠AOB=40°,∠DOE=30°,求∠BOD的度数;
(2)若∠AOD与∠BOD互补,且∠DOE=35°,求∠AOC的度数.
解:(1)∵OB是∠AOC的平分线,OD是∠COE的平分线,
∴∠COB=∠BOA=40°,∠COD=∠DOE=30°,
∴∠BOD=∠COD+∠COB=70°.
(2)由题意得
∠AOD+∠BOD=180°,
∵OD平分∠COE,∠DOE=35°,
∴∠COD=∠DOE=35°.
设∠AOB=x,则∠AOD=2x+35°,
∠BOD=x+35°,
∴2x+35°+x+35°=180°,
解得x=,
∴∠AOC=2x=.
25.(本题满分11分)在直线l上任取一点A,截取AB=16 cm,再截取AC=40 cm,求AB的中点D与AC的中点E之间的距离.
解:分两种情况:
(1)当点B,
点C位于点A同旁时,如图①,
因为AB=16 cm,AC=40 cm,点D,E分别是AB,AC中点,
所以AD=AB=8 cm,AE=AC=20 cm,
所以DE=AE-AD=20-8=12 cm.
(2)当点B,C位于点A两旁时,如图②.
因为AB=16 cm,AC=40 cm,点D,E分别是AB,AC中点,
则AD=AB=8 cm,AE=AC=20 cm,
所以DE=AD+AE=8 cm+20 cm=28 cm.
故AB的中点D与AC的中点E之间的距离为12 cm或28 cm.
26.(本题满分10分)(辽宁期末)【阅读】小白遇到这样一个问题:
如图,点C是线段AB的中点,AD=DB,CD=10,求AB的长.
eq \o(\s\up7(),\s\do5(①))
小白的思路是:设AB=x,根据“CD=10”列方程,请按照小白的思路完成此问题的解答.
【解决问题】用学过的知识或参考小白的方法,解决下面的问题:
已知OC,OD是∠AOB的内部的两条射线,∠AOC=∠AOB,∠AOD=m∠DOB,∠COD=n°.
(1)如图②,若m=,n=22,求∠DOB的度数;
(2)如图③,若n=14(3-2m)求∠DOB的度数.
eq \o(\s\up7(),\s\do5(②)) eq \o(\s\up7(),\s\do5(③))
解:【阅读】
∵点C为AB中点,AB=x,∴AC=AB=x.
∵AD=DB,∴AD=AB=x,
∴CD=AC-AD=x-x=x.
∵CD=10,则x=10,解得x=120.
故AB的长为120.
【解决问题】
∵∠AOD=m∠DOB,
∴∠AOB=∠AOD+∠DOB=(m+1)∠DOB.
∵∠AOC=∠AOB,
∴∠AOC=∠AOB=(m+1)∠DOB,
∴∠COD=∠AOC-∠AOD=(m+1)·∠DOB-m∠DOB
=∠DOB.
又∵∠COD=n°,∴∠DOB=n°,
解得∠DOB=.
(1)若m=,n=22,则
∠DOB===70°,
故∠DOB的度数为70°.
(2)若n=14(3-2m),则
∠DOB==70°,
故∠DOB的度数为70°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
湘教版七年级数学上册 名校优选精练 第四章检测题
班级:________姓名:________考号:________
(本试卷分第Ⅰ卷和第Ⅱ卷,考试时间:120分钟,赋分:120分)
第Ⅰ卷(选择题 共36分)
一、选择题(本大题共12小题,每小题3分,共36分)
1.下面四个图形中,是三棱柱的平面展开图的是( )
eq \o(\s\up7(),\s\do5(A)) eq \o(\s\up7(),\s\do5(B)) eq \o(\s\up7(),\s\do5(C)) eq \o(\s\up7(),\s\do5(D))
2.下列画图的语句中,正确的是( )
A.画直线AB=10 cm B.画射线OB=10 cm
C.延长射线BA到C,使BA=BC D.画线段CD=2 cm
3.如图,小亮为将一个衣架固定在墙上,他在衣架两端各用一个钉子进行固定,用数学知识解释他这样操作的原因,应该是( )
A.过一点有无数条直线
B.两点之间线段的长度,叫做这两点之间的距离
C.经过两点有且只有一条直线
D.两点之间,线段最短
4.不能用一副三角板画出的角是( )
A.15° B.75° C.105° D.125°
5.54.27°用度、分、秒表示为( )
A.54°16′26″ B.54°28′ C.54°16′15″ D.54°16′12″
6.如图,已知线段AB=18 cm,M为AB的中点,点C在线段AB上且CB=AB,则线段MC的长为( )
A.1 cm B.2 cm C.3 cm D.4 cm
7.(江西期末)若将一副三角板按如图所示的不同方式摆放,则图中∠α与∠β相等的是( )
eq \o(\s\up7(),\s\do5(A)) eq \o(\s\up7(),\s\do5(B)) eq \o(\s\up7(),\s\do5(C)) eq \o(\s\up7(),\s\do5(D))
8.当钟表的时间为10 ∶30时,时针与分针的夹角是( )
A.95° B.125° C.135° D.145°
9.如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠AOD=104°,则∠BOM等于( )
A.144° B.142° C.104° D.38°
第9题图 第10题图
10.(江苏期末)如图,该表面展开图按虚线折叠成正方体后,相对面上的两个数互为相反数,则(x+y)的值为( )
A.-2 B.-3 C.2 D.1
11.(河北期末)如图,下列关于图中线段之间的关系一定正确的是( )
A.x=2a+2b-c B.c-b=2a-2b
C.x+b=2a+c-b D.x+2a=3c+2b
12.如图所示,以O为端点画六条射线OA,OB,OC,OD,OE,OF后,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线上所描的点依次记为1,2,3,4,5,6,7,8,…,那么所描的第2 021个点在射线( )
A.OE上B.OF上C.OA上D.OB上
第Ⅱ卷(非选择题 共84分)
二、填空题(本大题共6小题,每小题3分,共18分)
13.用小立方块搭一个几何体,如图所示,这样的几何体最少需要 个小立方块,最多需要 个小立方块.
eq \o(\s\up7(),\s\do5(第13题图)) eq \o(\s\up7(),\s\do5(第14题图))
14.如图所示,∠AOB=85°,∠AOC=10°,OD是∠BOC的平分线,则∠BOD的度数为 度.
15.如图,四位同学画线段x=a-b+c,其中只有一位的答案是正确的,则这位同学所画的图是 .
16.(辽宁期末)已知A,B,C三点在同一条直线上,AB=8,BC=6,M,N分别是AB,BC的中点,则线段MN的长是 .
17.如图,已知∠AOC=∠COD=∠BOD=60°,则图中互补的角有 对.
将线段AB延长至点C,使BC=AB,延长BC至点D,使CD=BC,延长CD至点E,使DE=CD,若CE=8 cm,则AB= cm.
三、解答题(本大题共8小题,满分66分,解答应写出文字说明或演算步骤)
19.(本题满分10分)计算:
(1)32°19′+16°53′16″; (2)72°35′+18°33′×4.
20.(本题满分5分)如图,已知线段a,b,c,用圆规和直尺画线段,使它等于2a+b-3c.(不写作法,保留作图痕迹)
21.(本题满分6分)一个角的补角比它的余角的3倍少30°,求这个角和它的余角.
22.(本题满分8分)如图,O在直线AC上,OD是∠AOB的平分线,OE在∠BOC内.
(1)若OE是∠BOC的平分线,则有∠DOE=90°,试说明理由;
(2)若∠BOE=∠EOC,∠DOE=72°,求∠EOC的度数.
23.(本题满分8分)如图所示,B,C两点把线段AD分成4∶5∶7三部分,点E是线段AD的中点,CD=14 cm,求:
(1)EC的长; (2)AB ∶BE的值.
24.(本题满分8分)(湖北期末)如图,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)若∠AOB=40°,∠DOE=30°,求∠BOD的度数;
(2)若∠AOD与∠BOD互补,且∠DOE=35°,求∠AOC的度数.
25.(本题满分11分)在直线l上任取一点A,截取AB=16 cm,再截取AC=40 cm,求AB的中点D与AC的中点E之间的距离.
26.(本题满分10分)(辽宁期末)【阅读】小白遇到这样一个问题:
如图,点C是线段AB的中点,AD=DB,CD=10,求AB的长.
eq \o(\s\up7(),\s\do5(①))
小白的思路是:设AB=x,根据“CD=10”列方程,请按照小白的思路完成此问题的解答.
【解决问题】用学过的知识或参考小白的方法,解决下面的问题:
已知OC,OD是∠AOB的内部的两条射线,∠AOC=∠AOB,∠AOD=m∠DOB,∠COD=n°.
(1)如图②,若m=,n=22,求∠DOB的度数;
(2)如图③,若n=14(3-2m)求∠DOB的度数.
eq \o(\s\up7(),\s\do5(②)) eq \o(\s\up7(),\s\do5(③))
参考答案
第Ⅰ卷(选择题 共36分)
一、选择题(本大题共12小题,每小题3分,共36分)
1.下面四个图形中,是三棱柱的平面展开图的是(C)
eq \o(\s\up7(),\s\do5(A)) eq \o(\s\up7(),\s\do5(B)) eq \o(\s\up7(),\s\do5(C)) eq \o(\s\up7(),\s\do5(D))
2.下列画图的语句中,正确的是(D)
A.画直线AB=10 cm B.画射线OB=10 cm
C.延长射线BA到C,使BA=BC D.画线段CD=2 cm
3.如图,小亮为将一个衣架固定在墙上,他在衣架两端各用一个钉子进行固定,用数学知识解释他这样操作的原因,应该是(C)
A.过一点有无数条直线
B.两点之间线段的长度,叫做这两点之间的距离
C.经过两点有且只有一条直线
D.两点之间,线段最短
4.不能用一副三角板画出的角是(D)
A.15° B.75° C.105° D.125°
5.54.27°用度、分、秒表示为(D)
A.54°16′26″ B.54°28′ C.54°16′15″ D.54°16′12″
6.如图,已知线段AB=18 cm,M为AB的中点,点C在线段AB上且CB=AB,则线段MC的长为(C)
A.1 cm B.2 cm C.3 cm D.4 cm
7.(江西期末)若将一副三角板按如图所示的不同方式摆放,则图中∠α与∠β相等的是(A)
eq \o(\s\up7(),\s\do5(A)) eq \o(\s\up7(),\s\do5(B)) eq \o(\s\up7(),\s\do5(C)) eq \o(\s\up7(),\s\do5(D))
8.当钟表的时间为10 ∶30时,时针与分针的夹角是(C)
A.95° B.125° C.135° D.145°
9.如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠AOD=104°,则∠BOM等于(B)
A.144° B.142° C.104° D.38°
第9题图 第10题图
10.(江苏期末)如图,该表面展开图按虚线折叠成正方体后,相对面上的两个数互为相反数,则(x+y)的值为(C)
A.-2 B.-3 C.2 D.1
11.(河北期末)如图,下列关于图中线段之间的关系一定正确的是(C)
A.x=2a+2b-c B.c-b=2a-2b
C.x+b=2a+c-b D.x+2a=3c+2b
12.如图所示,以O为端点画六条射线OA,OB,OC,OD,OE,OF后,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线上所描的点依次记为1,2,3,4,5,6,7,8,…,那么所描的第2 021个点在射线(A)
A.OE上B.OF上C.OA上D.OB上
第Ⅱ卷(非选择题 共84分)
二、填空题(本大题共6小题,每小题3分,共18分)
13.用小立方块搭一个几何体,如图所示,这样的几何体最少需要9个小立方块,最多需要13个小立方块.
eq \o(\s\up7(),\s\do5(第13题图)) eq \o(\s\up7(),\s\do5(第14题图))
14.如图所示,∠AOB=85°,∠AOC=10°,OD是∠BOC的平分线,则∠BOD的度数为37.5度.
15.如图,四位同学画线段x=a-b+c,其中只有一位的答案是正确的,则这位同学所画的图是③.
16.(辽宁期末)已知A,B,C三点在同一条直线上,AB=8,BC=6,M,N分别是AB,BC的中点,则线段MN的长是1或7.
17.如图,已知∠AOC=∠COD=∠BOD=60°,
则图中互补的角有6对.
将线段AB延长至点C,使BC=AB,延长BC至点D,使CD=BC,延长CD至点E,使DE=CD,若CE=8 cm,
则AB=54cm.
三、解答题(本大题共8小题,满分66分,解答应写出文字说明或演算步骤)
19.(本题满分10分)计算:
(1)32°19′+16°53′16″;
解:32°19′+16°53′16″=49°12′16″.
(2)72°35′+18°33′×4.
解:72°35′+18°33′×4
=72°35′+72°132′
=72°35′+74°12′
=146°47′.
20.(本题满分5分)如图,已知线段a,b,c,用圆规和直尺画线段,使它等于2a+b-3c.(不写作法,保留作图痕迹)
解:作图略.
21.(本题满分6分)一个角的补角比它的余角的3倍少30°,求这个角和它的余角.
解:设这个角为x°,
则3(90-x)-30=180-x,
解得x=30,
所以90°-30°=60°.
答:这个角为30°,它的余角为60°.
22.(本题满分8分)如图,O在直线AC上,OD是∠AOB的平分线,OE在∠BOC内.
(1)若OE是∠BOC的平分线,则有∠DOE=90°,试说明理由;
(2)若∠BOE=∠EOC,∠DOE=72°,求∠EOC的度数.
解:(1)因为OD是∠AOB的平分线,OE是∠BOC的平分线,
所以∠BOD=∠AOB,∠BOE=∠BOC,
所以∠DOE=(∠AOB+∠BOC)
=∠AOC=90°.
(2)设∠EOB=x,则∠EOC=2x,
则∠BOD=(180°-3x),
则∠BOE+∠BOD=∠DOE,
即x+(180°-3x)=72°,
解得x=36°,
故∠EOC=2x=72°.
23.(本题满分8分)如图所示,B,C两点把线段AD分成4∶5∶7三部分,点E是线段AD的中点,CD=14 cm,求:
(1)EC的长;
解:设线段AB,BC,CD分别为4x cm,5x cm,7x cm,
则∵CD=7x=14,∴x=2.
∵AB=4x=8 cm,BC=5x=10 cm,
∴AD=AB+BC+CD=8+10+14=32 cm,
故EC=AD-CD=×32-14=2 cm.
(2)AB ∶BE的值.
解:∵BC=10 cm,EC=2 cm,
∴BE=BC-EC=10-2=8 cm,
又∵AB=8 cm,
∴AB∶ BE=8∶8=1.
24.(本题满分8分)(湖北期末)如图,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)若∠AOB=40°,∠DOE=30°,求∠BOD的度数;
(2)若∠AOD与∠BOD互补,且∠DOE=35°,求∠AOC的度数.
解:(1)∵OB是∠AOC的平分线,OD是∠COE的平分线,
∴∠COB=∠BOA=40°,∠COD=∠DOE=30°,
∴∠BOD=∠COD+∠COB=70°.
(2)由题意得
∠AOD+∠BOD=180°,
∵OD平分∠COE,∠DOE=35°,
∴∠COD=∠DOE=35°.
设∠AOB=x,则∠AOD=2x+35°,
∠BOD=x+35°,
∴2x+35°+x+35°=180°,
解得x=,
∴∠AOC=2x=.
25.(本题满分11分)在直线l上任取一点A,截取AB=16 cm,再截取AC=40 cm,求AB的中点D与AC的中点E之间的距离.
解:分两种情况:
(1)当点B,
点C位于点A同旁时,如图①,
因为AB=16 cm,AC=40 cm,点D,E分别是AB,AC中点,
所以AD=AB=8 cm,AE=AC=20 cm,
所以DE=AE-AD=20-8=12 cm.
(2)当点B,C位于点A两旁时,如图②.
因为AB=16 cm,AC=40 cm,点D,E分别是AB,AC中点,
则AD=AB=8 cm,AE=AC=20 cm,
所以DE=AD+AE=8 cm+20 cm=28 cm.
故AB的中点D与AC的中点E之间的距离为12 cm或28 cm.
26.(本题满分10分)(辽宁期末)【阅读】小白遇到这样一个问题:
如图,点C是线段AB的中点,AD=DB,CD=10,求AB的长.
eq \o(\s\up7(),\s\do5(①))
小白的思路是:设AB=x,根据“CD=10”列方程,请按照小白的思路完成此问题的解答.
【解决问题】用学过的知识或参考小白的方法,解决下面的问题:
已知OC,OD是∠AOB的内部的两条射线,∠AOC=∠AOB,∠AOD=m∠DOB,∠COD=n°.
(1)如图②,若m=,n=22,求∠DOB的度数;
(2)如图③,若n=14(3-2m)求∠DOB的度数.
eq \o(\s\up7(),\s\do5(②)) eq \o(\s\up7(),\s\do5(③))
解:【阅读】
∵点C为AB中点,AB=x,∴AC=AB=x.
∵AD=DB,∴AD=AB=x,
∴CD=AC-AD=x-x=x.
∵CD=10,则x=10,解得x=120.
故AB的长为120.
【解决问题】
∵∠AOD=m∠DOB,
∴∠AOB=∠AOD+∠DOB=(m+1)∠DOB.
∵∠AOC=∠AOB,
∴∠AOC=∠AOB=(m+1)∠DOB,
∴∠COD=∠AOC-∠AOD=(m+1)·∠DOB-m∠DOB
=∠DOB.
又∵∠COD=n°,∴∠DOB=n°,
解得∠DOB=.
(1)若m=,n=22,则
∠DOB===70°,
故∠DOB的度数为70°.
(2)若n=14(3-2m),则
∠DOB==70°,
故∠DOB的度数为70°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
