北师大版2021-2022学年七年级数学上册4.4角的比较 同步达标测评(word版、含解析)
文档属性
| 名称 | 北师大版2021-2022学年七年级数学上册4.4角的比较 同步达标测评(word版、含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 144.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 00:00:00 | ||
图片预览


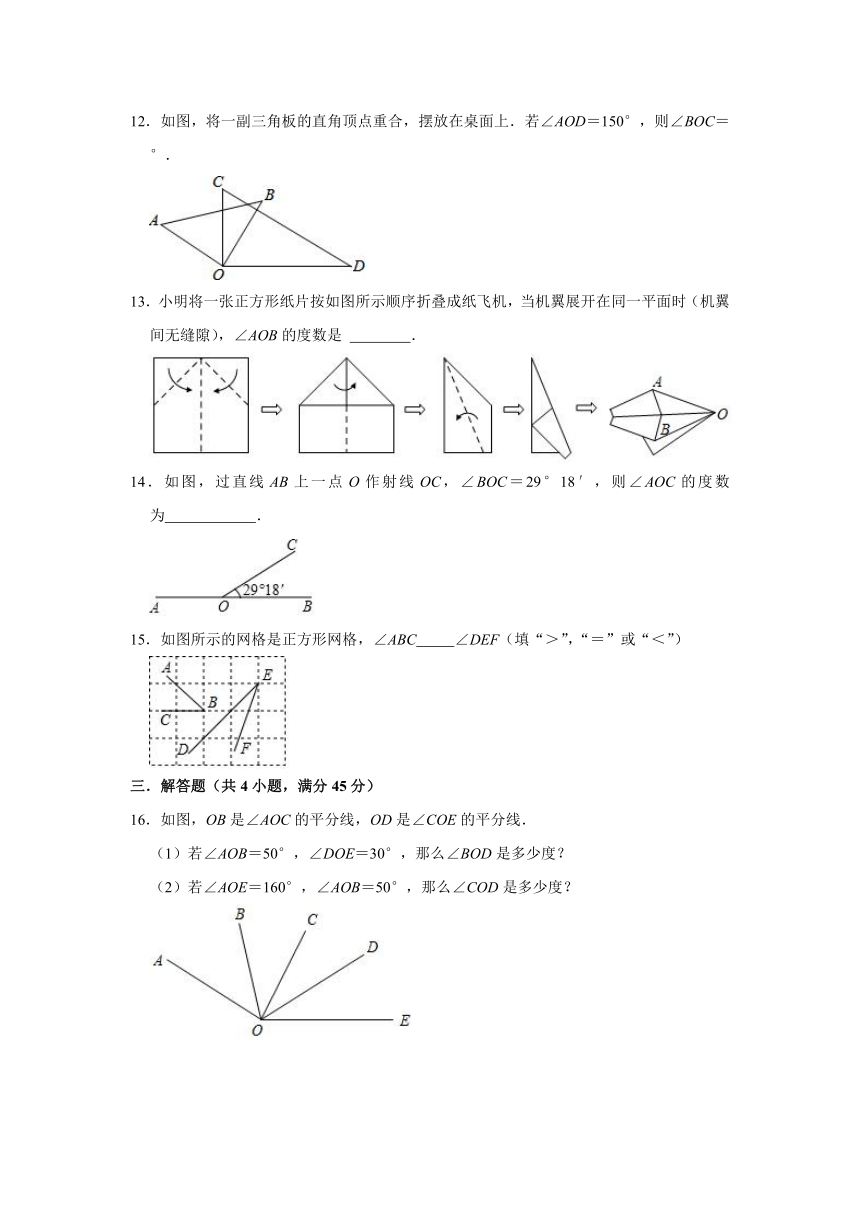


文档简介
2021-2022学年北师大版七年级数学上册《4.4角的比较》同步达标测评(附答案)
一.选择题(共8小题,满分40分)
1.已知∠AOB=20°,∠AOC=4∠AOB,OD平分∠AOB,OM平分∠AOC,则∠MOD的度数是( )
A.20°或50° B.20°或60° C.30°或50° D.30°或60°
2.如图所示,已知O是直线AB上一点,∠1=68°,OD平分∠BOC,则∠2的度数是( )
A.40° B.45° C.44° D.46°
3.如图,下列结论中,不能说明射线OC平分∠AOB的是( )
A.∠AOC=∠BOC B.∠AOB=2∠BOC
C.∠AOB=2∠AOC D.∠AOC+∠BOC=∠BOA
4.如图,若OC是∠AOB内部的一条射线,则下列式子中,不能表示“OC是∠AOB的角平分线”的是( )
A.∠AOC=∠BOC B.∠AOB=2∠BOC
C. D.∠AOC+∠BOC=∠AOB
5.如图,长方形纸片ABCD,M为AD边的中点,将纸片沿BM,CM折叠,使点A落在点A1处,点D落在点D1处,若∠1=30°,则∠BMC=( )
A.135° B.120° C.105° D.100°
6.用一副三角板拼成的图形如图所示,其中B、C、D三点在同一条直线上.则图中∠ACE的大小为( )
A.45° B.60° C.75° D.105°
7.已知∠α=39°18′,∠β=39.18°,∠γ=39.3°,下面结论正确的是( )
A.∠α<∠γ<∠β B.∠γ>∠α=∠β C.∠α=∠γ>∠β D.∠γ<∠α<∠β
8.下列说法正确的个数是( )
(1)连接两点之间的线段叫两点间的距离;
(2)木匠师傅锯木料时,一般先在模板上画出两个点,然后过这两点弹出一条墨线,这样做的原理是:两点之间,线段最短;
(3)若AB=2CB,则点C是AB的中点;
(4)若∠A=20°18′.∠B=20°28″,∠C=20.25°,则有∠A>∠C>∠B.
A.1个 B.2个 C.3个 D.4个
二.填空题(共7小题,满分35分)
9.如图,已知O是直线AB上一点,OD平分∠BOC,∠2=80°,∠1的度数是 .
10.如图,点O是直线AB上一点,OD平分∠AOC,OE平分∠BOC,若∠COE等于64°,则∠AOD等于 度.
11.如图,OM是∠AOB的平分线,∠AOB=140°.∠AOD=100°,那么∠DOM= 度.
12.如图,将一副三角板的直角顶点重合,摆放在桌面上.若∠AOD=150°,则∠BOC= °.
13.小明将一张正方形纸片按如图所示顺序折叠成纸飞机,当机翼展开在同一平面时(机翼间无缝隙),∠AOB的度数是 .
14.如图,过直线AB上一点O作射线OC,∠BOC=29°18′,则∠AOC的度数为 .
15.如图所示的网格是正方形网格,∠ABC ∠DEF(填“>”,“=”或“<”)
三.解答题(共4小题,满分45分)
16.如图,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)若∠AOB=50°,∠DOE=30°,那么∠BOD是多少度?
(2)若∠AOE=160°,∠AOB=50°,那么∠COD是多少度?
17.补全下面的解题过程:
如图,已知OC是∠AOB内部的一条射线,OD是∠AOB的平分线,∠AOC=2∠BOC且∠BOC=40°,求∠COD的度数.
解:因为∠AOC=2∠BOC,∠BOC=40°,
所以∠AOC= °,
所以∠AOB=∠AOC+∠ = °.
因为OD平分∠AOB,
所以∠AOD=∠ = °,
所以∠COD=∠ ﹣∠AOD= °.
18.如图,∠AOB是平角,∠DOE=90°,OC平分∠DOB.
(1)若∠AOE=32°,求∠BOC的度数;
(2)若OD是∠AOC的角平分线,求∠AOE的度数.
19.如图,BD平分∠ABC,BE把∠ABC分成2:5的两部分,∠DBE=21°,求∠ABC的度数.
20.如图,O为直线AB上一点,OC为射线,OD,OE分别为∠AOC,∠BOC的平分线.
(1)判断射线OD,OE的位置关系,并说明理由;
(2)若∠AOD=30°,试说明OC为∠AOE的平分线.
参考答案
一.选择题(共8小题,满分40分)
1.
解:分为两种情况:如图1,当∠AOB在∠AOC内部时,
∵∠AOB=20°,∠AOC=4∠AOB,
∴∠AOC=80°,
∵OD平分∠AOB,OM平分∠AOC,
∴∠AOD=∠BOD=∠AOB=10°,∠AOM=∠COM=∠AOC=40°,
∴∠DOM=∠AOM﹣∠AOD=40°﹣10°=30°;
如图2,当∠AOB在∠AOC外部时,
∠DOM=∠AOM+∠AOD=40°+10°=50°;
故选:C.
2.解:∵OD平分∠BOC,
∴∠BOC=2∠1=2×68°=136°,
∴∠2=180°﹣∠BOC=180°﹣136°=44°.
故选:C.
3.解:A、∵∠AOC=∠BOC,∴OC平分∠AOB,故A正确;
B、∵∠AOB=2∠BOC,∠AOB=∠AOC+∠BO,C∴∠AOC=∠BOC,故B正确;
C、∵∠AOB=2∠BOC,∠AOB=∠AOC+∠BOC,∴∠AOC=∠BOC,故C正确;
D、∵∠AOC+∠BOC=∠AOB,∠AOC不一定等于∠BOC,故D错误;
故选:D.
4.解:A、∵∠AOC=∠BOC,
∴OC平分∠AOB,
即OC是∠AOB的角平分线,正确,故本选项错误;
B、∵∠AOB=2∠BOC=∠AOC+∠BOC,
∴∠AOC=∠BOC,
∴OC平分∠AOB,
即OC是∠AOB的角平分线,正确,故本选项错误;
C、∵∠AOC=∠AOB,
∴∠AOB=2∠AOC=∠AOC+∠BOC,
∴∠AOC=∠BOC,
∴OC平分∠AOB,
即OC是∠AOB的角平分线,正确,故本选项错误;
D、∵∠AOC+∠BOC=∠AOB,
∴假如∠AOC=30°,∠BOC=40°,∠AOB=70°,符合上式,但是OC不是∠AOB的角平分线,故本选项正确.
故选:D.
5.解:∵∠1=30°
∴∠AMA1+∠DMD1=180°﹣30°=150°
∵将纸片沿BM,CM折叠,使点A落在点A1处,点D落在点D1处,
∴MB平分∠AMA1,MC平分∠DMD1
∴∠BMA1+∠CMD1=(∠AMA1+∠DMD1)=75°
∴∠BMC=∠1+∠BMA1+∠CMD1=30°+75°=105°
故选:C.
6.解:∵B、C、D三点在同一条直线上.
∴∠ACE=180°﹣60°﹣45°=75°.
故选:C.
7.解:∵∠α=39°18′=39.3°,39.18°<39.3°,
∴∠α=∠γ>∠β.
故选:C.
8.解:(1)连接两点之间的线段的长度叫两点间的距离,错误;
(2)木匠师傅锯木料时,一般先在模板上画出两个点,然后过这两点弹出一条墨线,这样做的原理是:两点确定一条直线,错误;
(3)当C在线段AB上,且AB=2CB时,点C是AB的中点,当C不在线段AB上时,则不是中点,故命题错误;
(4)若∠A=20°18′.∠B=20°28″,∠C=20.25°,则有∠A>∠C>∠B,正确;
故选:A.
二.填空题(共7小题,满分35分)
9.解:∵OD平分∠BOC,∠2=80°,
∴∠COD=∠2=80°,
∴∠1=180°﹣∠COD﹣∠2=180°﹣80°﹣80°=20°.
故答案为:20°.
10.解:∵OE平分∠BOC,∠COE=64°
∴∠BOC=2∠COE=128°
∴∠AOC=180°﹣∠BOC=180°﹣128=52°
∵OD平分∠AOC
∴∠AOD=∠AOC=×52°=26°.
11.解:∵OM是∠AOB的平分线,∠AOB=140°,
∴∠AOM=∠AOB=140°=70°,
∵∠AOD=100°,
∴∠DOM=∠AOD﹣∠AOM=100°﹣70°=30°.
故答案为:30.
12.解:∵∠AOB=∠COD=90°,∠AOD=150°
∴∠BOC=∠AOB+∠COD﹣∠AOD=90°+90°﹣150°=30°.
故答案为:30.
13.解:在折叠过程中角一直是轴对称的折叠,
∠AOB=22.5°×2=45°;
故答案为45°.
14.解:∵∠BOC=29°18′,
∴∠AOC的度数为:180°﹣29°18′=150°42′.
故答案为:150°42′.
15.解:由图可得,∠ABC=45°,∠DEF<45°,
∴∠ABC>∠DEF,
故答案为:>.
三.解答题(共5小题,满分44分)
16.解:(1)OB是∠AOC的平分线,
∴∠BOC=∠AOB=50°;
∵OD是∠COE的平分线,
∴∠COD=∠DOE=30°,
∴∠BOD=∠BOC+∠COD=50°+30°=80°;
(2)OB是∠AOC的平分线,
∴∠AOC=2∠AOB=100°,
∴∠COE=∠AOE﹣∠AOC=160°﹣100°=60°,
∵OD是∠COE的平分线,
∴∠COD=∠COE=30°.
17.解:∵∠AOC=2∠BOC,∠BOC=40°.
∴∠AOC=80°.
∴∠AOB=∠AOC+∠BOC=120°.
∵OD平分∠AOB.
∴∠AOD=∠AOB=60°.
∴∠COD=∠AOC﹣∠AOD=20°.
故答案为:80,BOC,120,AOB,60,AOC,20.
18.解:(1)∠AOD=∠DOE﹣∠AOE=90°﹣32°=58°
∠BOD=∠AOB﹣∠AOD=180°﹣58°=122°
又OC平分∠BOD
所以:∠BOC=∠BOD=×122°=61°
(2)因为OC平分∠BOD,OD平分∠AOC
所以∠BOC=∠DOC=∠AOD
又∠BOC+∠DOC+∠AOD=180°
所以∠AOD=×180°=60°
所以∠AOE=∠DOE﹣∠AOD=90°﹣60°=30°
19.解:设∠ABE=2x°,
得2x+21=5x﹣21,
解得x=14,
∴∠ABC=14°×7=98°.
∴∠ABC的度数是98°
20.解:(1)OD⊥OE.
理由:∵OD,OE分别为∠AOC,∠BOC的平分线,
∴∠COD=∠AOC,∠COE=∠BOC,
∵∠AOC+∠BOC=180°,
∴∠DOE=∠COD+∠COE=(∠AOC+∠BOC)=90°,
∴OD⊥OE.
(2)∵∠AOD=30°,OD平分∠AOC,
∴∠AOC=2∠AOD=60°
∵∠DOE=90°,
∴∠AOE=∠AOD+∠DOE=30°+90°=120°,
∴∠AOE=2∠AOC,
∴OC为∠AOE的平分线.
一.选择题(共8小题,满分40分)
1.已知∠AOB=20°,∠AOC=4∠AOB,OD平分∠AOB,OM平分∠AOC,则∠MOD的度数是( )
A.20°或50° B.20°或60° C.30°或50° D.30°或60°
2.如图所示,已知O是直线AB上一点,∠1=68°,OD平分∠BOC,则∠2的度数是( )
A.40° B.45° C.44° D.46°
3.如图,下列结论中,不能说明射线OC平分∠AOB的是( )
A.∠AOC=∠BOC B.∠AOB=2∠BOC
C.∠AOB=2∠AOC D.∠AOC+∠BOC=∠BOA
4.如图,若OC是∠AOB内部的一条射线,则下列式子中,不能表示“OC是∠AOB的角平分线”的是( )
A.∠AOC=∠BOC B.∠AOB=2∠BOC
C. D.∠AOC+∠BOC=∠AOB
5.如图,长方形纸片ABCD,M为AD边的中点,将纸片沿BM,CM折叠,使点A落在点A1处,点D落在点D1处,若∠1=30°,则∠BMC=( )
A.135° B.120° C.105° D.100°
6.用一副三角板拼成的图形如图所示,其中B、C、D三点在同一条直线上.则图中∠ACE的大小为( )
A.45° B.60° C.75° D.105°
7.已知∠α=39°18′,∠β=39.18°,∠γ=39.3°,下面结论正确的是( )
A.∠α<∠γ<∠β B.∠γ>∠α=∠β C.∠α=∠γ>∠β D.∠γ<∠α<∠β
8.下列说法正确的个数是( )
(1)连接两点之间的线段叫两点间的距离;
(2)木匠师傅锯木料时,一般先在模板上画出两个点,然后过这两点弹出一条墨线,这样做的原理是:两点之间,线段最短;
(3)若AB=2CB,则点C是AB的中点;
(4)若∠A=20°18′.∠B=20°28″,∠C=20.25°,则有∠A>∠C>∠B.
A.1个 B.2个 C.3个 D.4个
二.填空题(共7小题,满分35分)
9.如图,已知O是直线AB上一点,OD平分∠BOC,∠2=80°,∠1的度数是 .
10.如图,点O是直线AB上一点,OD平分∠AOC,OE平分∠BOC,若∠COE等于64°,则∠AOD等于 度.
11.如图,OM是∠AOB的平分线,∠AOB=140°.∠AOD=100°,那么∠DOM= 度.
12.如图,将一副三角板的直角顶点重合,摆放在桌面上.若∠AOD=150°,则∠BOC= °.
13.小明将一张正方形纸片按如图所示顺序折叠成纸飞机,当机翼展开在同一平面时(机翼间无缝隙),∠AOB的度数是 .
14.如图,过直线AB上一点O作射线OC,∠BOC=29°18′,则∠AOC的度数为 .
15.如图所示的网格是正方形网格,∠ABC ∠DEF(填“>”,“=”或“<”)
三.解答题(共4小题,满分45分)
16.如图,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)若∠AOB=50°,∠DOE=30°,那么∠BOD是多少度?
(2)若∠AOE=160°,∠AOB=50°,那么∠COD是多少度?
17.补全下面的解题过程:
如图,已知OC是∠AOB内部的一条射线,OD是∠AOB的平分线,∠AOC=2∠BOC且∠BOC=40°,求∠COD的度数.
解:因为∠AOC=2∠BOC,∠BOC=40°,
所以∠AOC= °,
所以∠AOB=∠AOC+∠ = °.
因为OD平分∠AOB,
所以∠AOD=∠ = °,
所以∠COD=∠ ﹣∠AOD= °.
18.如图,∠AOB是平角,∠DOE=90°,OC平分∠DOB.
(1)若∠AOE=32°,求∠BOC的度数;
(2)若OD是∠AOC的角平分线,求∠AOE的度数.
19.如图,BD平分∠ABC,BE把∠ABC分成2:5的两部分,∠DBE=21°,求∠ABC的度数.
20.如图,O为直线AB上一点,OC为射线,OD,OE分别为∠AOC,∠BOC的平分线.
(1)判断射线OD,OE的位置关系,并说明理由;
(2)若∠AOD=30°,试说明OC为∠AOE的平分线.
参考答案
一.选择题(共8小题,满分40分)
1.
解:分为两种情况:如图1,当∠AOB在∠AOC内部时,
∵∠AOB=20°,∠AOC=4∠AOB,
∴∠AOC=80°,
∵OD平分∠AOB,OM平分∠AOC,
∴∠AOD=∠BOD=∠AOB=10°,∠AOM=∠COM=∠AOC=40°,
∴∠DOM=∠AOM﹣∠AOD=40°﹣10°=30°;
如图2,当∠AOB在∠AOC外部时,
∠DOM=∠AOM+∠AOD=40°+10°=50°;
故选:C.
2.解:∵OD平分∠BOC,
∴∠BOC=2∠1=2×68°=136°,
∴∠2=180°﹣∠BOC=180°﹣136°=44°.
故选:C.
3.解:A、∵∠AOC=∠BOC,∴OC平分∠AOB,故A正确;
B、∵∠AOB=2∠BOC,∠AOB=∠AOC+∠BO,C∴∠AOC=∠BOC,故B正确;
C、∵∠AOB=2∠BOC,∠AOB=∠AOC+∠BOC,∴∠AOC=∠BOC,故C正确;
D、∵∠AOC+∠BOC=∠AOB,∠AOC不一定等于∠BOC,故D错误;
故选:D.
4.解:A、∵∠AOC=∠BOC,
∴OC平分∠AOB,
即OC是∠AOB的角平分线,正确,故本选项错误;
B、∵∠AOB=2∠BOC=∠AOC+∠BOC,
∴∠AOC=∠BOC,
∴OC平分∠AOB,
即OC是∠AOB的角平分线,正确,故本选项错误;
C、∵∠AOC=∠AOB,
∴∠AOB=2∠AOC=∠AOC+∠BOC,
∴∠AOC=∠BOC,
∴OC平分∠AOB,
即OC是∠AOB的角平分线,正确,故本选项错误;
D、∵∠AOC+∠BOC=∠AOB,
∴假如∠AOC=30°,∠BOC=40°,∠AOB=70°,符合上式,但是OC不是∠AOB的角平分线,故本选项正确.
故选:D.
5.解:∵∠1=30°
∴∠AMA1+∠DMD1=180°﹣30°=150°
∵将纸片沿BM,CM折叠,使点A落在点A1处,点D落在点D1处,
∴MB平分∠AMA1,MC平分∠DMD1
∴∠BMA1+∠CMD1=(∠AMA1+∠DMD1)=75°
∴∠BMC=∠1+∠BMA1+∠CMD1=30°+75°=105°
故选:C.
6.解:∵B、C、D三点在同一条直线上.
∴∠ACE=180°﹣60°﹣45°=75°.
故选:C.
7.解:∵∠α=39°18′=39.3°,39.18°<39.3°,
∴∠α=∠γ>∠β.
故选:C.
8.解:(1)连接两点之间的线段的长度叫两点间的距离,错误;
(2)木匠师傅锯木料时,一般先在模板上画出两个点,然后过这两点弹出一条墨线,这样做的原理是:两点确定一条直线,错误;
(3)当C在线段AB上,且AB=2CB时,点C是AB的中点,当C不在线段AB上时,则不是中点,故命题错误;
(4)若∠A=20°18′.∠B=20°28″,∠C=20.25°,则有∠A>∠C>∠B,正确;
故选:A.
二.填空题(共7小题,满分35分)
9.解:∵OD平分∠BOC,∠2=80°,
∴∠COD=∠2=80°,
∴∠1=180°﹣∠COD﹣∠2=180°﹣80°﹣80°=20°.
故答案为:20°.
10.解:∵OE平分∠BOC,∠COE=64°
∴∠BOC=2∠COE=128°
∴∠AOC=180°﹣∠BOC=180°﹣128=52°
∵OD平分∠AOC
∴∠AOD=∠AOC=×52°=26°.
11.解:∵OM是∠AOB的平分线,∠AOB=140°,
∴∠AOM=∠AOB=140°=70°,
∵∠AOD=100°,
∴∠DOM=∠AOD﹣∠AOM=100°﹣70°=30°.
故答案为:30.
12.解:∵∠AOB=∠COD=90°,∠AOD=150°
∴∠BOC=∠AOB+∠COD﹣∠AOD=90°+90°﹣150°=30°.
故答案为:30.
13.解:在折叠过程中角一直是轴对称的折叠,
∠AOB=22.5°×2=45°;
故答案为45°.
14.解:∵∠BOC=29°18′,
∴∠AOC的度数为:180°﹣29°18′=150°42′.
故答案为:150°42′.
15.解:由图可得,∠ABC=45°,∠DEF<45°,
∴∠ABC>∠DEF,
故答案为:>.
三.解答题(共5小题,满分44分)
16.解:(1)OB是∠AOC的平分线,
∴∠BOC=∠AOB=50°;
∵OD是∠COE的平分线,
∴∠COD=∠DOE=30°,
∴∠BOD=∠BOC+∠COD=50°+30°=80°;
(2)OB是∠AOC的平分线,
∴∠AOC=2∠AOB=100°,
∴∠COE=∠AOE﹣∠AOC=160°﹣100°=60°,
∵OD是∠COE的平分线,
∴∠COD=∠COE=30°.
17.解:∵∠AOC=2∠BOC,∠BOC=40°.
∴∠AOC=80°.
∴∠AOB=∠AOC+∠BOC=120°.
∵OD平分∠AOB.
∴∠AOD=∠AOB=60°.
∴∠COD=∠AOC﹣∠AOD=20°.
故答案为:80,BOC,120,AOB,60,AOC,20.
18.解:(1)∠AOD=∠DOE﹣∠AOE=90°﹣32°=58°
∠BOD=∠AOB﹣∠AOD=180°﹣58°=122°
又OC平分∠BOD
所以:∠BOC=∠BOD=×122°=61°
(2)因为OC平分∠BOD,OD平分∠AOC
所以∠BOC=∠DOC=∠AOD
又∠BOC+∠DOC+∠AOD=180°
所以∠AOD=×180°=60°
所以∠AOE=∠DOE﹣∠AOD=90°﹣60°=30°
19.解:设∠ABE=2x°,
得2x+21=5x﹣21,
解得x=14,
∴∠ABC=14°×7=98°.
∴∠ABC的度数是98°
20.解:(1)OD⊥OE.
理由:∵OD,OE分别为∠AOC,∠BOC的平分线,
∴∠COD=∠AOC,∠COE=∠BOC,
∵∠AOC+∠BOC=180°,
∴∠DOE=∠COD+∠COE=(∠AOC+∠BOC)=90°,
∴OD⊥OE.
(2)∵∠AOD=30°,OD平分∠AOC,
∴∠AOC=2∠AOD=60°
∵∠DOE=90°,
∴∠AOE=∠AOD+∠DOE=30°+90°=120°,
∴∠AOE=2∠AOC,
∴OC为∠AOE的平分线.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
