华东师大版七年级数学上册 名校优选精练 第五章 相交线与平行线 单元检测题(含答案)
文档属性
| 名称 | 华东师大版七年级数学上册 名校优选精练 第五章 相交线与平行线 单元检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 510.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 08:36:55 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
华东师大版七年级数学上册 名校优选精练 第五章检测题
(全卷三个大题,共24个小题,满分120分,考试用时:120分钟)
班级:________姓名:________考号:________
一、选择题(每小题3分,共30分)
1.如图,直线a,b相交于点O,若∠1=50°,则∠2与∠3的度数分别是( )
A.50°,40° B.50°,130°
C.130°,50° D.50°,50°
2.(兰州中考)如图,AB∥CD,AE∥CF,∠A=50°,则∠C=( )
A.40° B.50° C.60° D.70°
3.(孝感中考)如图,直线AB,CD相交于点O,OE⊥CD,垂足为点O.若∠BOE=40°,则∠AOC的度数为( )
A.40° B.50° C.60° D.140°
4.(慈溪中考)下列四组图形中,有一组中的两个图形经过平移其中一个,能得到另一个,这组是( )
5.如图,描述同位角、内错角、同旁内角关系不正确的是( )
A.∠1与∠4是同位角
B.∠2与∠3是内错角
C.∠3与∠4是同旁内角
D.∠2与∠4是同旁内角
6.(攀枝花中考)如图,平行线AB,CD被直线EF所截,过点B作BG⊥EF于点G,已知∠1=50°,则∠B=( )
A.20° B.30° C.40° D.50°
7.(荆门中考)已知直线a∥b,将一块含45°角的直角三角板(∠C=90°)按如图所示的位置摆放,若∠1=55°,则∠2的度数为( )
A.80° B.70° C.85° D.75°
8.(宁夏中考)将一个长方形纸片按如图所示折叠,若∠1=40°,则∠2的度数是( )
A.40° B.50° C.60° D.70°
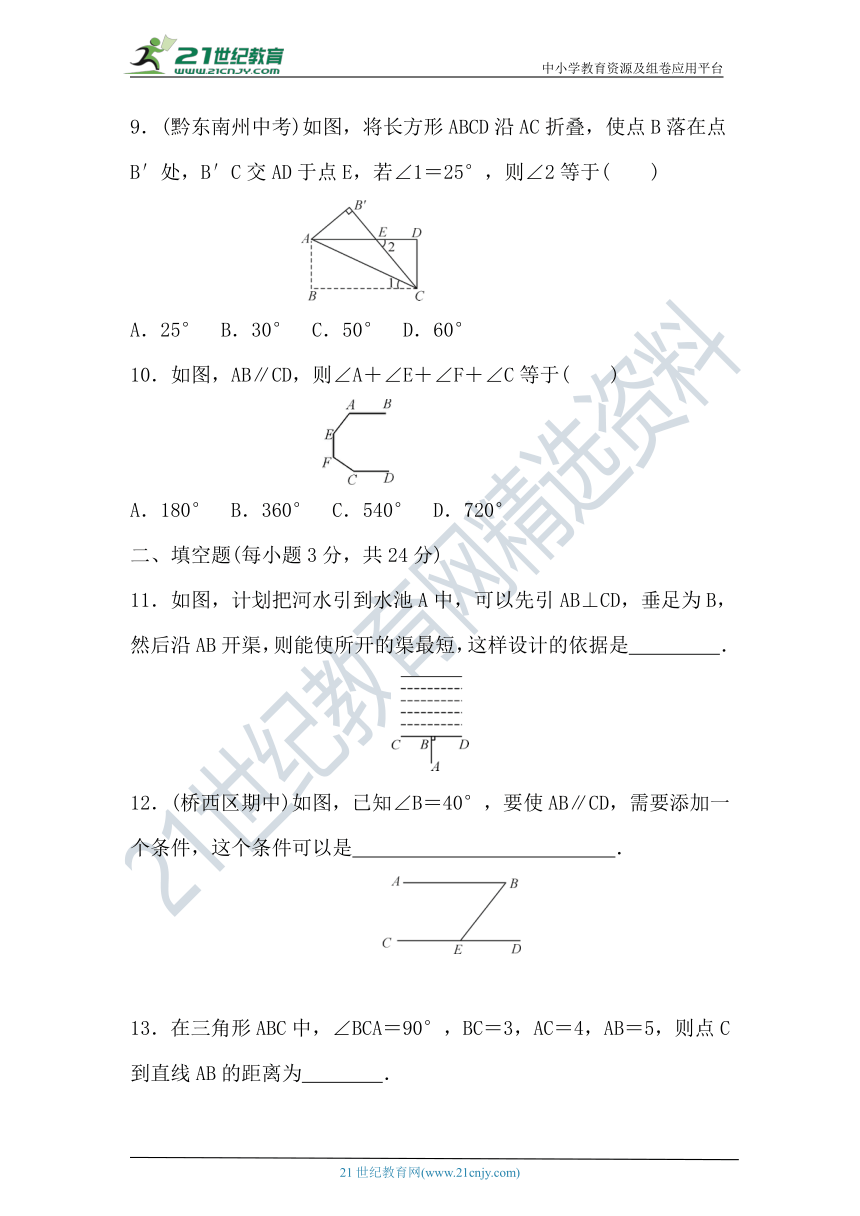
9.(黔东南州中考)如图,将长方形ABCD沿AC折叠,使点B落在点B′处,B′C交AD于点E,若∠1=25°,则∠2等于( )
A.25° B.30° C.50° D.60°
10.如图,AB∥CD,则∠A+∠E+∠F+∠C等于( )
A.180° B.360° C.540° D.720°
二、填空题(每小题3分,共24分)
11.如图,计划把河水引到水池A中,可以先引AB⊥CD,垂足为B,然后沿AB开渠,则能使所开的渠最短,这样设计的依据是 .
12.(桥西区期中)如图,已知∠B=40°,要使AB∥CD,需要添加一个条件,这个条件可以是 .
13.在三角形ABC中,∠BCA=90°,BC=3,AC=4,AB=5,则点C到直线AB的距离为 .
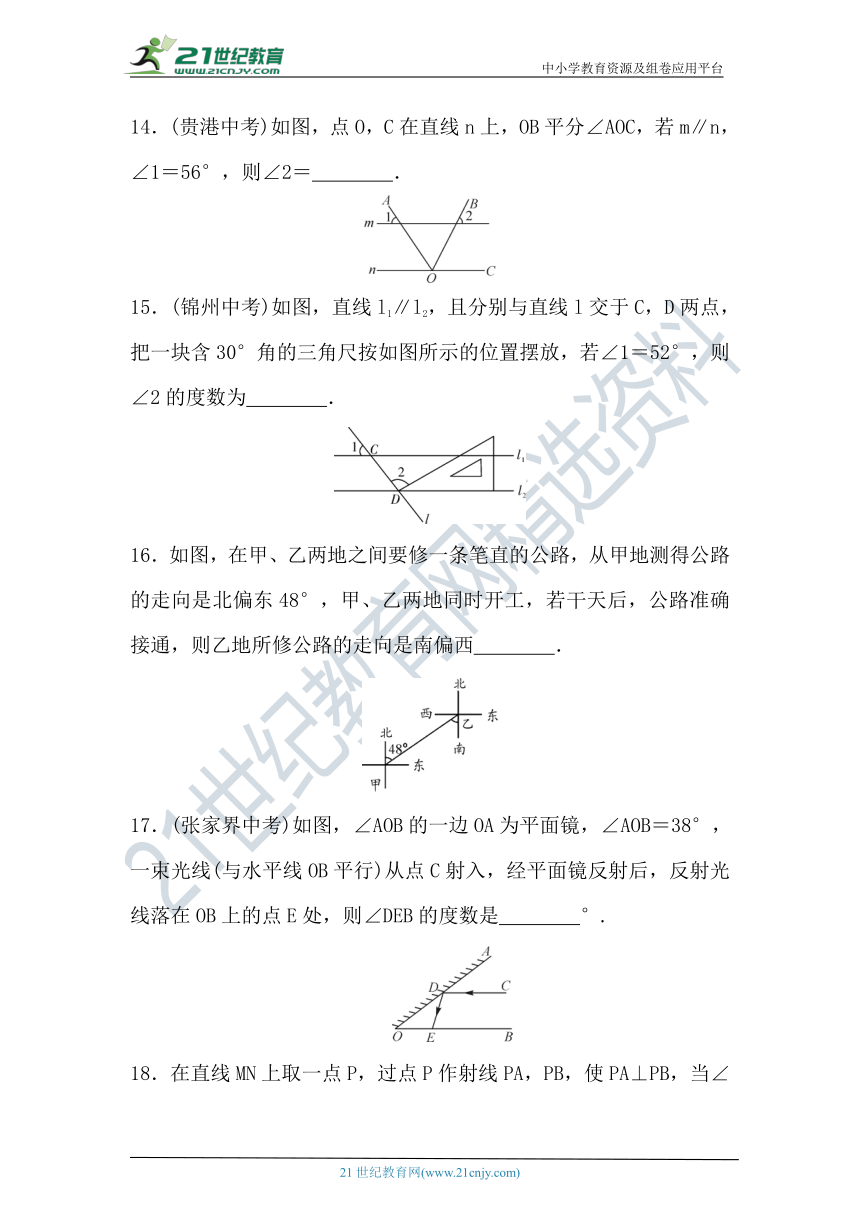
14.(贵港中考)如图,点O,C在直线n上,OB平分∠AOC,若m∥n,∠1=56°,则∠2= .
15.(锦州中考)如图,直线l1∥l2,且分别与直线l交于C,D两点,把一块含30°角的三角尺按如图所示的位置摆放,若∠1=52°,则∠2的度数为 .
16.如图,在甲、乙两地之间要修一条笔直的公路,从甲地测得公路的走向是北偏东48°,甲、乙两地同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西 .
17.(张家界中考)如图,∠AOB的一边OA为平面镜,∠AOB=38°,一束光线(与水平线OB平行)从点C射入,经平面镜反射后,反射光线落在OB上的点E处,则∠DEB的度数是 °.
18.在直线MN上取一点P,过点P作射线PA,PB,使PA⊥PB,当∠MPA=40°时,∠NPB的度数是 .
三、解答题(共66分)
19.(12分)如图,∠AOB内部有一点P,∠AOB=60°.
(1)过点P作直线PC∥OB,交OA于点C;
(2)过点P作直线PD⊥OB,垂足为点D,交OA于点E;
(3)过点C画直线OB的垂线段CF.
A
. P
O B
20.(8分)如图,直线AB与直线CD相交于点O,OE⊥AB,OF平分∠AOD,∠COE=28°.求∠AOC和∠DOF的度数.
21.(10分)(青山区期中)如图,直线AB,CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOD的对顶角为 ,∠DOE的邻补角为 ;
(2)若∠AOC=90°,且∠BOE∶∠EOD=2∶3.求∠EOC的度数.
22.(12分)(丹东期末)如图,已知∠1+∠2=180°,∠3=∠B.
(1)试判断DE与BC的位置关系,并说明理由;
(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.
解:(1)DE∥BC,
理由:
23.(12分)如图,∠FED=∠AHD,∠GFA=40°,∠HAQ=15°,∠ACB=70°,且AQ平分∠FAC.试说明:BD∥GE∥AH.
24.(12分)将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°,∠E=∠B=45°).
(1)①若∠DCE=45°,则∠ACB的度数为 ;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由;
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.
参考答案
一、选择题(每小题3分,共30分)
1.如图,直线a,b相交于点O,若∠1=50°,则∠2与∠3的度数分别是( B )
A.50°,40° B.50°,130°
C.130°,50° D.50°,50°
2.(兰州中考)如图,AB∥CD,AE∥CF,∠A=50°,则∠C=( B )
A.40° B.50° C.60° D.70°
3.(孝感中考)如图,直线AB,CD相交于点O,OE⊥CD,垂足为点O.若∠BOE=40°,则∠AOC的度数为( B )
A.40° B.50° C.60° D.140°
4.(慈溪中考)下列四组图形中,有一组中的两个图形经过平移其中一个,能得到另一个,这组是(B)
5.如图,描述同位角、内错角、同旁内角关系不正确的是(D)
A.∠1与∠4是同位角
B.∠2与∠3是内错角
C.∠3与∠4是同旁内角
D.∠2与∠4是同旁内角
6.(攀枝花中考)如图,平行线AB,CD被直线EF所截,过点B作BG⊥EF于点G,已知∠1=50°,则∠B=( C )
A.20° B.30° C.40° D.50°
7.(荆门中考)已知直线a∥b,将一块含45°角的直角三角板(∠C=90°)按如图所示的位置摆放,若∠1=55°,则∠2的度数为(A)
A.80° B.70° C.85° D.75°
8.(宁夏中考)将一个长方形纸片按如图所示折叠,若∠1=40°,则∠2的度数是(D)
A.40° B.50° C.60° D.70°
9.(黔东南州中考)如图,将长方形ABCD沿AC折叠,使点B落在点B′处,B′C交AD于点E,若∠1=25°,则∠2等于( C )
A.25° B.30° C.50° D.60°
10.如图,AB∥CD,则∠A+∠E+∠F+∠C等于( C )
A.180° B.360° C.540° D.720°
【解析】过E,F分别作AB的平行线,由平行线的性质即可解得.
二、填空题(每小题3分,共24分)
11.如图,计划把河水引到水池A中,可以先引AB⊥CD,垂足为B,然后沿AB开渠,则能使所开的渠最短,这样设计的依据是__垂线段最短__.
12.(桥西区期中)如图,已知∠B=40°,要使AB∥CD,需要添加一个条件,这个条件可以是__∠BED=40°(答案不唯一)__.
13.在三角形ABC中,∠BCA=90°,BC=3,AC=4,AB=5,则点C到直线AB的距离为2.4.
14.(贵港中考)如图,点O,C在直线n上,OB平分∠AOC,若m∥n,∠1=56°,则∠2=__62°__.
15.(锦州中考)如图,直线l1∥l2,且分别与直线l交于C,D两点,把一块含30°角的三角尺按如图所示的位置摆放,若∠1=52°,则∠2的度数为98°.
16.如图,在甲、乙两地之间要修一条笔直的公路,从甲地测得公路的走向是北偏东48°,甲、乙两地同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西__48°__.
17.(张家界中考)如图,∠AOB的一边OA为平面镜,∠AOB=38°,一束光线(与水平线OB平行)从点C射入,经平面镜反射后,反射光线落在OB上的点E处,则∠DEB的度数是__76__°.
18.在直线MN上取一点P,过点P作射线PA,PB,使PA⊥PB,当∠MPA=40°时,∠NPB的度数是50°或130°.
【解析】分A,B在直线MN的同侧和异侧两种情况求解.
三、解答题(共66分)
19.(12分)如图,∠AOB内部有一点P,∠AOB=60°.
(1)过点P作直线PC∥OB,交OA于点C;
(2)过点P作直线PD⊥OB,垂足为点D,交OA于点E;
(3)过点C画直线OB的垂线段CF.
解:(1)如图,直线PC即为所求作.
(2)如图,直线PD即为所求作.
(3)如图,线段CF即为所求作.
20.(8分)如图,直线AB与直线CD相交于点O,OE⊥AB,OF平分∠AOD,∠COE=28°.求∠AOC和∠DOF的度数.
解:∵OE⊥AB,
∴∠AOE=90°,
∴∠AOC=∠AOE-∠COE=62°,
∴∠AOD=180°-∠AOC=118°.
∵OF平分∠AOD,
∴∠DOF=∠AOD=59°.
21.(10分)(青山区期中)如图,直线AB,CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOD的对顶角为__∠BOC__,∠DOE的邻补角为__∠COE__;
(2)若∠AOC=90°,且∠BOE∶∠EOD=2∶3.求∠EOC的度数.
解:(1)∠AOD的对顶角为∠BOC,∠DOE的邻补角为∠COE;
故答案为∠BOC,∠COE.
(2)∵∠DOB=∠AOC=90°,∠DOB=∠BOE+∠EOD,
∠BOE∶∠EOD=2∶3,
∴∠EOD=∠BOE,
∴∠BOE+∠BOE=90°,
∴∠BOE=36°,
∴∠DOE=54°,
∴∠EOC=180°-∠DOE=126°.
22.(12分)(丹东期末)如图,已知∠1+∠2=180°,∠3=∠B.
(1)试判断DE与BC的位置关系,并说明理由;
(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.
解:(1)DE∥BC,
理由:
∵∠1+∠4=180°,∠1+∠2=180°,
∴∠2=∠4,∴AB∥EF,∴∠3=∠5,
∵∠3=∠B,
∴∠5=∠B,∴DE∥BC.
(2)∵DE平分∠ADC,∴∠5=∠6,
∵∠2=3∠B,∴∠2+∠5+∠6=3∠B+∠B+∠B=180°,
∴∠B=36°,∴∠2=108°,
∵∠1+∠2=180°,∴∠1=72°.
23.(12分)如图,∠FED=∠AHD,∠GFA=40°,∠HAQ=15°,∠ACB=70°,且AQ平分∠FAC.试说明:BD∥GE∥AH.
解:∵∠FED=∠AHD,∴GE∥AH.
∵∠GFA=40°,∴∠FAH=40°.
∵AQ平分∠FAC,∴∠CAQ=∠FAQ.
又∵∠HAQ=15°,
∴∠CAQ=∠FAQ=∠HAQ+∠FAH=15°+40°=55°,
∴∠CAH=∠CAQ+∠HAQ=55°+15°=70°.
∵∠ACB=70°,
∴∠ACB=∠CAH,∴AH∥BD,∴BD∥GE.∴BD∥GE∥AH.
24.(12分)将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°,∠E=∠B=45°).
(1)①若∠DCE=45°,则∠ACB的度数为135°;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由;
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.
解:(1)②∵∠ACB=140°,∠ACD=90°,
∴∠DCB=140°-90°=50°,
∴∠DCE=90°-50°=40°.
(2)∠ACB+∠DCE=180°.理由:
∵∠ACB=∠ACD+∠DCB=90°+∠DCB,
∴∠ACB+∠DCE=90°+∠DCB+∠DCE=90°+90°=180°.
(3)存在,
当∠ACE=30°时,AD∥BC;
当∠ACE=∠E=45°时,AC∥BE;
当∠ACE=120°时,AD∥CE;
当∠ACE=135°时,BE∥CD;
当∠ACE=165°时,BE∥AD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
华东师大版七年级数学上册 名校优选精练 第五章检测题
(全卷三个大题,共24个小题,满分120分,考试用时:120分钟)
班级:________姓名:________考号:________
一、选择题(每小题3分,共30分)
1.如图,直线a,b相交于点O,若∠1=50°,则∠2与∠3的度数分别是( )
A.50°,40° B.50°,130°
C.130°,50° D.50°,50°
2.(兰州中考)如图,AB∥CD,AE∥CF,∠A=50°,则∠C=( )
A.40° B.50° C.60° D.70°
3.(孝感中考)如图,直线AB,CD相交于点O,OE⊥CD,垂足为点O.若∠BOE=40°,则∠AOC的度数为( )
A.40° B.50° C.60° D.140°
4.(慈溪中考)下列四组图形中,有一组中的两个图形经过平移其中一个,能得到另一个,这组是( )
5.如图,描述同位角、内错角、同旁内角关系不正确的是( )
A.∠1与∠4是同位角
B.∠2与∠3是内错角
C.∠3与∠4是同旁内角
D.∠2与∠4是同旁内角
6.(攀枝花中考)如图,平行线AB,CD被直线EF所截,过点B作BG⊥EF于点G,已知∠1=50°,则∠B=( )
A.20° B.30° C.40° D.50°
7.(荆门中考)已知直线a∥b,将一块含45°角的直角三角板(∠C=90°)按如图所示的位置摆放,若∠1=55°,则∠2的度数为( )
A.80° B.70° C.85° D.75°
8.(宁夏中考)将一个长方形纸片按如图所示折叠,若∠1=40°,则∠2的度数是( )
A.40° B.50° C.60° D.70°
9.(黔东南州中考)如图,将长方形ABCD沿AC折叠,使点B落在点B′处,B′C交AD于点E,若∠1=25°,则∠2等于( )
A.25° B.30° C.50° D.60°
10.如图,AB∥CD,则∠A+∠E+∠F+∠C等于( )
A.180° B.360° C.540° D.720°
二、填空题(每小题3分,共24分)
11.如图,计划把河水引到水池A中,可以先引AB⊥CD,垂足为B,然后沿AB开渠,则能使所开的渠最短,这样设计的依据是 .
12.(桥西区期中)如图,已知∠B=40°,要使AB∥CD,需要添加一个条件,这个条件可以是 .
13.在三角形ABC中,∠BCA=90°,BC=3,AC=4,AB=5,则点C到直线AB的距离为 .
14.(贵港中考)如图,点O,C在直线n上,OB平分∠AOC,若m∥n,∠1=56°,则∠2= .
15.(锦州中考)如图,直线l1∥l2,且分别与直线l交于C,D两点,把一块含30°角的三角尺按如图所示的位置摆放,若∠1=52°,则∠2的度数为 .
16.如图,在甲、乙两地之间要修一条笔直的公路,从甲地测得公路的走向是北偏东48°,甲、乙两地同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西 .
17.(张家界中考)如图,∠AOB的一边OA为平面镜,∠AOB=38°,一束光线(与水平线OB平行)从点C射入,经平面镜反射后,反射光线落在OB上的点E处,则∠DEB的度数是 °.
18.在直线MN上取一点P,过点P作射线PA,PB,使PA⊥PB,当∠MPA=40°时,∠NPB的度数是 .
三、解答题(共66分)
19.(12分)如图,∠AOB内部有一点P,∠AOB=60°.
(1)过点P作直线PC∥OB,交OA于点C;
(2)过点P作直线PD⊥OB,垂足为点D,交OA于点E;
(3)过点C画直线OB的垂线段CF.
A
. P
O B
20.(8分)如图,直线AB与直线CD相交于点O,OE⊥AB,OF平分∠AOD,∠COE=28°.求∠AOC和∠DOF的度数.
21.(10分)(青山区期中)如图,直线AB,CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOD的对顶角为 ,∠DOE的邻补角为 ;
(2)若∠AOC=90°,且∠BOE∶∠EOD=2∶3.求∠EOC的度数.
22.(12分)(丹东期末)如图,已知∠1+∠2=180°,∠3=∠B.
(1)试判断DE与BC的位置关系,并说明理由;
(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.
解:(1)DE∥BC,
理由:
23.(12分)如图,∠FED=∠AHD,∠GFA=40°,∠HAQ=15°,∠ACB=70°,且AQ平分∠FAC.试说明:BD∥GE∥AH.
24.(12分)将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°,∠E=∠B=45°).
(1)①若∠DCE=45°,则∠ACB的度数为 ;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由;
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.
参考答案
一、选择题(每小题3分,共30分)
1.如图,直线a,b相交于点O,若∠1=50°,则∠2与∠3的度数分别是( B )
A.50°,40° B.50°,130°
C.130°,50° D.50°,50°
2.(兰州中考)如图,AB∥CD,AE∥CF,∠A=50°,则∠C=( B )
A.40° B.50° C.60° D.70°
3.(孝感中考)如图,直线AB,CD相交于点O,OE⊥CD,垂足为点O.若∠BOE=40°,则∠AOC的度数为( B )
A.40° B.50° C.60° D.140°
4.(慈溪中考)下列四组图形中,有一组中的两个图形经过平移其中一个,能得到另一个,这组是(B)
5.如图,描述同位角、内错角、同旁内角关系不正确的是(D)
A.∠1与∠4是同位角
B.∠2与∠3是内错角
C.∠3与∠4是同旁内角
D.∠2与∠4是同旁内角
6.(攀枝花中考)如图,平行线AB,CD被直线EF所截,过点B作BG⊥EF于点G,已知∠1=50°,则∠B=( C )
A.20° B.30° C.40° D.50°
7.(荆门中考)已知直线a∥b,将一块含45°角的直角三角板(∠C=90°)按如图所示的位置摆放,若∠1=55°,则∠2的度数为(A)
A.80° B.70° C.85° D.75°
8.(宁夏中考)将一个长方形纸片按如图所示折叠,若∠1=40°,则∠2的度数是(D)
A.40° B.50° C.60° D.70°
9.(黔东南州中考)如图,将长方形ABCD沿AC折叠,使点B落在点B′处,B′C交AD于点E,若∠1=25°,则∠2等于( C )
A.25° B.30° C.50° D.60°
10.如图,AB∥CD,则∠A+∠E+∠F+∠C等于( C )
A.180° B.360° C.540° D.720°
【解析】过E,F分别作AB的平行线,由平行线的性质即可解得.
二、填空题(每小题3分,共24分)
11.如图,计划把河水引到水池A中,可以先引AB⊥CD,垂足为B,然后沿AB开渠,则能使所开的渠最短,这样设计的依据是__垂线段最短__.
12.(桥西区期中)如图,已知∠B=40°,要使AB∥CD,需要添加一个条件,这个条件可以是__∠BED=40°(答案不唯一)__.
13.在三角形ABC中,∠BCA=90°,BC=3,AC=4,AB=5,则点C到直线AB的距离为2.4.
14.(贵港中考)如图,点O,C在直线n上,OB平分∠AOC,若m∥n,∠1=56°,则∠2=__62°__.
15.(锦州中考)如图,直线l1∥l2,且分别与直线l交于C,D两点,把一块含30°角的三角尺按如图所示的位置摆放,若∠1=52°,则∠2的度数为98°.
16.如图,在甲、乙两地之间要修一条笔直的公路,从甲地测得公路的走向是北偏东48°,甲、乙两地同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西__48°__.
17.(张家界中考)如图,∠AOB的一边OA为平面镜,∠AOB=38°,一束光线(与水平线OB平行)从点C射入,经平面镜反射后,反射光线落在OB上的点E处,则∠DEB的度数是__76__°.
18.在直线MN上取一点P,过点P作射线PA,PB,使PA⊥PB,当∠MPA=40°时,∠NPB的度数是50°或130°.
【解析】分A,B在直线MN的同侧和异侧两种情况求解.
三、解答题(共66分)
19.(12分)如图,∠AOB内部有一点P,∠AOB=60°.
(1)过点P作直线PC∥OB,交OA于点C;
(2)过点P作直线PD⊥OB,垂足为点D,交OA于点E;
(3)过点C画直线OB的垂线段CF.
解:(1)如图,直线PC即为所求作.
(2)如图,直线PD即为所求作.
(3)如图,线段CF即为所求作.
20.(8分)如图,直线AB与直线CD相交于点O,OE⊥AB,OF平分∠AOD,∠COE=28°.求∠AOC和∠DOF的度数.
解:∵OE⊥AB,
∴∠AOE=90°,
∴∠AOC=∠AOE-∠COE=62°,
∴∠AOD=180°-∠AOC=118°.
∵OF平分∠AOD,
∴∠DOF=∠AOD=59°.
21.(10分)(青山区期中)如图,直线AB,CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOD的对顶角为__∠BOC__,∠DOE的邻补角为__∠COE__;
(2)若∠AOC=90°,且∠BOE∶∠EOD=2∶3.求∠EOC的度数.
解:(1)∠AOD的对顶角为∠BOC,∠DOE的邻补角为∠COE;
故答案为∠BOC,∠COE.
(2)∵∠DOB=∠AOC=90°,∠DOB=∠BOE+∠EOD,
∠BOE∶∠EOD=2∶3,
∴∠EOD=∠BOE,
∴∠BOE+∠BOE=90°,
∴∠BOE=36°,
∴∠DOE=54°,
∴∠EOC=180°-∠DOE=126°.
22.(12分)(丹东期末)如图,已知∠1+∠2=180°,∠3=∠B.
(1)试判断DE与BC的位置关系,并说明理由;
(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.
解:(1)DE∥BC,
理由:
∵∠1+∠4=180°,∠1+∠2=180°,
∴∠2=∠4,∴AB∥EF,∴∠3=∠5,
∵∠3=∠B,
∴∠5=∠B,∴DE∥BC.
(2)∵DE平分∠ADC,∴∠5=∠6,
∵∠2=3∠B,∴∠2+∠5+∠6=3∠B+∠B+∠B=180°,
∴∠B=36°,∴∠2=108°,
∵∠1+∠2=180°,∴∠1=72°.
23.(12分)如图,∠FED=∠AHD,∠GFA=40°,∠HAQ=15°,∠ACB=70°,且AQ平分∠FAC.试说明:BD∥GE∥AH.
解:∵∠FED=∠AHD,∴GE∥AH.
∵∠GFA=40°,∴∠FAH=40°.
∵AQ平分∠FAC,∴∠CAQ=∠FAQ.
又∵∠HAQ=15°,
∴∠CAQ=∠FAQ=∠HAQ+∠FAH=15°+40°=55°,
∴∠CAH=∠CAQ+∠HAQ=55°+15°=70°.
∵∠ACB=70°,
∴∠ACB=∠CAH,∴AH∥BD,∴BD∥GE.∴BD∥GE∥AH.
24.(12分)将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°,∠E=∠B=45°).
(1)①若∠DCE=45°,则∠ACB的度数为135°;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由;
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.
解:(1)②∵∠ACB=140°,∠ACD=90°,
∴∠DCB=140°-90°=50°,
∴∠DCE=90°-50°=40°.
(2)∠ACB+∠DCE=180°.理由:
∵∠ACB=∠ACD+∠DCB=90°+∠DCB,
∴∠ACB+∠DCE=90°+∠DCB+∠DCE=90°+90°=180°.
(3)存在,
当∠ACE=30°时,AD∥BC;
当∠ACE=∠E=45°时,AC∥BE;
当∠ACE=120°时,AD∥CE;
当∠ACE=135°时,BE∥CD;
当∠ACE=165°时,BE∥AD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
